5560.树的直径

蛮不错的一道题目,你要利用树的性质分析出,你只需要维护上一次的树的直径的两个端点就好了
#include<iostream>using namespace std;
using ll = long long;
using pii = pair<int,int>;
const int N = 6e5+10;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int qmi(int a,int b,int mod){int res=1;while(b){if(b&1)res=res*a%mod;b>>=1;a=a*a%mod;}return res;}int n,q,m;// int e[N],ne[N],w[N],h[N],idx;
// void add(int a,int b,int c){// e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
// }int dep[N];
int fa[N][22];int lca(int a,int b){if(dep[a]<dep[b])swap(a,b);for(int i=20;i>=0;--i)if(dep[fa[a][i]]>=dep[b])a = fa[a][i];if(a==b)return a;for(int i=20;i>=0;--i)if(fa[a][i]!=fa[b][i])a = fa[a][i],b =fa[b][i];return fa[a][0];}int dist(int a,int b){return dep[a]+dep[b]-2*dep[lca(a,b)];
}void solve()
{cin>>n;dep[2] = dep[3] = dep[4] = 2;dep[1] = 1;fa[1][0] = 0;fa[2][0] = fa[3][0] = fa[4][0] = 1;int tem = 4;int A = 2,B = 3;while(n--){int a;cin>>a;int b = ++tem,c = ++tem;fa[b][0] = a,fa[c][0] = a;dep[b] = dep[a]+1,dep[c] = dep[a]+1;for(int i=1;i<=20;i++)fa[b][i] = fa[fa[b][i-1]][i-1] ;for(int i=1;i<=20;i++)fa[c][i] = fa[fa[c][i-1]][i-1] ;int dista = dist(b,A),distb = dist(b,B);int dists = dist(A,B);//cout<<A<<" "<<B<<" "<<b<<" "<<dista<<" "<<distb<<" "<<dists<<"\n";if(dista<=dists&&distb<=dists){cout<<dists<<"\n";continue;}if(dista>dists&&dista>=distb){B=b;cout<<dista<<"\n";continue;}if(distb>dists){A=b;cout<<distb<<"\n";continue;}}}signed main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _;//cin>>_;_ = 1;while(_--)solve();return 0;
}相关文章:

5560.树的直径
蛮不错的一道题目,你要利用树的性质分析出,你只需要维护上一次的树的直径的两个端点就好了 #include<iostream>using namespace std; using ll long long; using pii pair<int,int>; const int N 6e510; const int inf 0x3f3f3f3f; cons…...
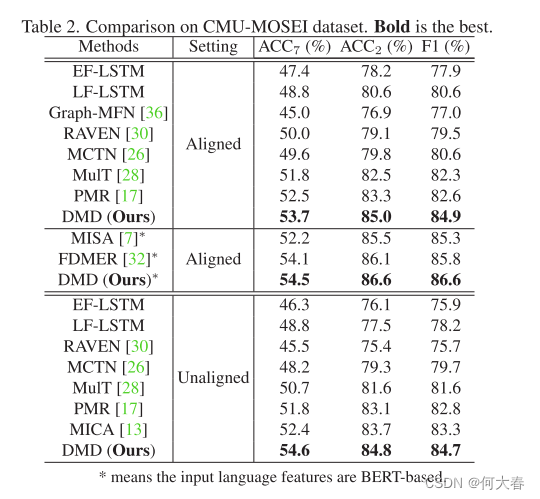
Decoupled Multimodal Distilling for Emotion Recognition 论文阅读
Decoupled Multimodal Distilling for Emotion Recognition 论文阅读 Abstract1. Introduction2. Related Works2.1. Multimodal emotion recognition2.2. Knowledge distillation3. The Proposed Method3.1. Multimodal feature decoupling3.2. GD with Decoupled Multimodal …...

【css】使用display:inline-block后,元素间存在4px的间隔
问题:在本地项目中使用【display: inline-block】,元素间存在4px间隔。打包后发布到外网又不存在这个问题了。 归根结底这是一个西文排版的问题,英文有空格作为词分界,而中文则没有。 此时的元素具有文本属性,只要标签…...

代码执行漏洞
原理:没有对接口输入的内容进行严格的判断 造成攻击者精心构造的代码非法执行 当应用在调用一些能将字符转化为代码的函数(如PHP中的eval)时,没有考虑用户是否能控 制这个字符串,这就会造成代码执行漏洞。 相 关 函 数 : PHP&…...

SQLServer2022安装
首先从官网上下载2022版本SQL Server 下载 | Microsoft 选择此把呢不能运行,适合我们在学习阶段使用。 同时网页往下滑动,下载SSMS 下载后的文件 注意:在运行时最好获取管理员权限运行,第一次在安装时未获取管理员权限最终…...

vue2 配置@指向src
使用的是vue cli创建的项目。 1.安装 path 如果在 Node.js 环境中运行代码,path 模块默认是可用的,则不需要单独安装,否则输入下面命令安装path npm i path -S 2.找到vue.config.js文件: const { defineConfig } require(vue/…...
用友U9 存在PatchFile.asmx接口任意文件上传漏洞
声明: 本文仅用于技术交流,请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 简介 用友U9是由中国用友软件股份有限公司开发的一款企业…...
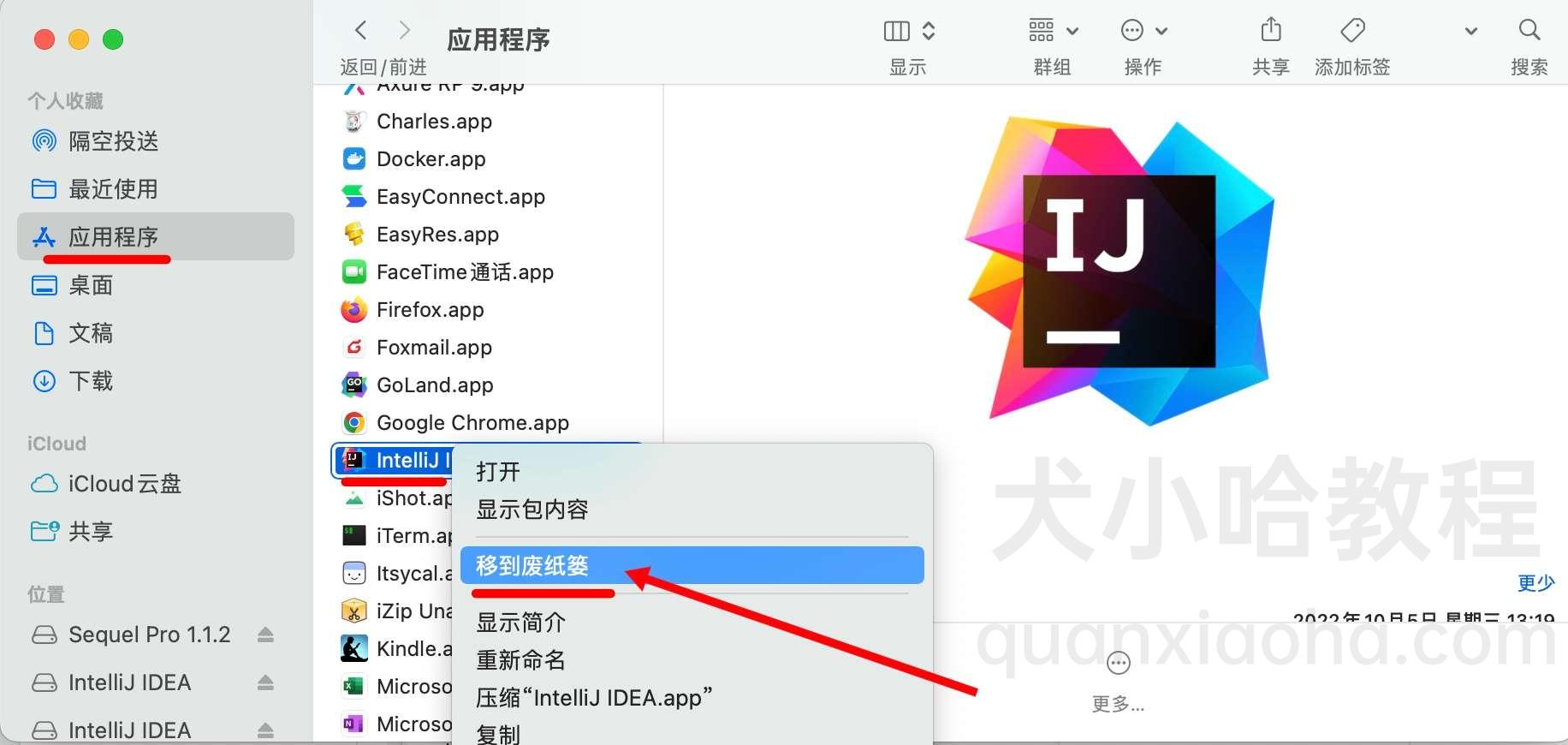
如何卸载干净 IDEA(图文讲解)
更新时间 2022-12-20 11:一则或许对你有用的小广告 星球 内第一个项目:全栈前后端分离博客项目,演示地址:Weblog 前后端分离博客, 1.0 版本已经更新完毕,正在更新 2.0 版本。采用技术栈 Spring Boot Mybatis Plus Vue 3.x Vit…...
Ansible 之进程管理模块)
自动化运维(十)Ansible 之进程管理模块
Ansible的进程管理模块提供了一种强大而灵活的方式来管理和操作各种进程管理器和服务。无论你使用的是Supervisor、Systemd、传统的init脚本还是Runit,这些模块都可以帮助你轻松地管理服务的生命周期。通过合理地使用这些模块,你可以实现服务的自动化管理,提高系统的可靠性和稳…...

【leetcode279】完全平方数,动态规划解法
原问题:给定一个非负整数n,如果把它视作一些完全平方数的和,那么最少需要多少个完全平方数? 这次学习到一个热心网友的解法:把问题转化兑换零钱问题,然后使用动态规划求解。 比如,给定 n12, 那…...
)
Java 元素排序(数组、List 集合)
数组元素排序 升序 int[] array {3, 1, 4, 5}; Arrays.sort(array);// 升序排序 System.out.println(Arrays.toString(array)); //输出:[1, 3, 4, 5]降序 可以先将数组元素存入 List 集合,然后集合元素逆序,最后将集合元素写回原数组。&a…...
使用vite创建一个react18项目
一、vite是什么? vite 是一种新型前端构建工具,能够显著提升前端开发体验。它主要由两部分组成: 一个开发服务器,它基于原生 ES 模块提供了丰富的内建功能,如速度快到惊人的模块热更新(HMR)。 …...
(leetcode 78))
子集(迭代)(leetcode 78)
核心逻辑: 根据子数组包含的元素个数迭代: 现有子集的基础上通过添加这个新元素来翻倍子集的数量 f(n)2f(n−1) vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ans;int i,j,k;ans.p…...

汽车疲劳测试试验平台技术要求(北重厂家)
汽车疲劳测试试验平台技术要求通常包括以下几个方面: 车辆加载能力:测试平台需要具备足够的承载能力,能够同时测试多种车型和不同重量的车辆。 动力系统:测试平台需要具备稳定可靠的动力系统,能够提供足够的力和速度来…...
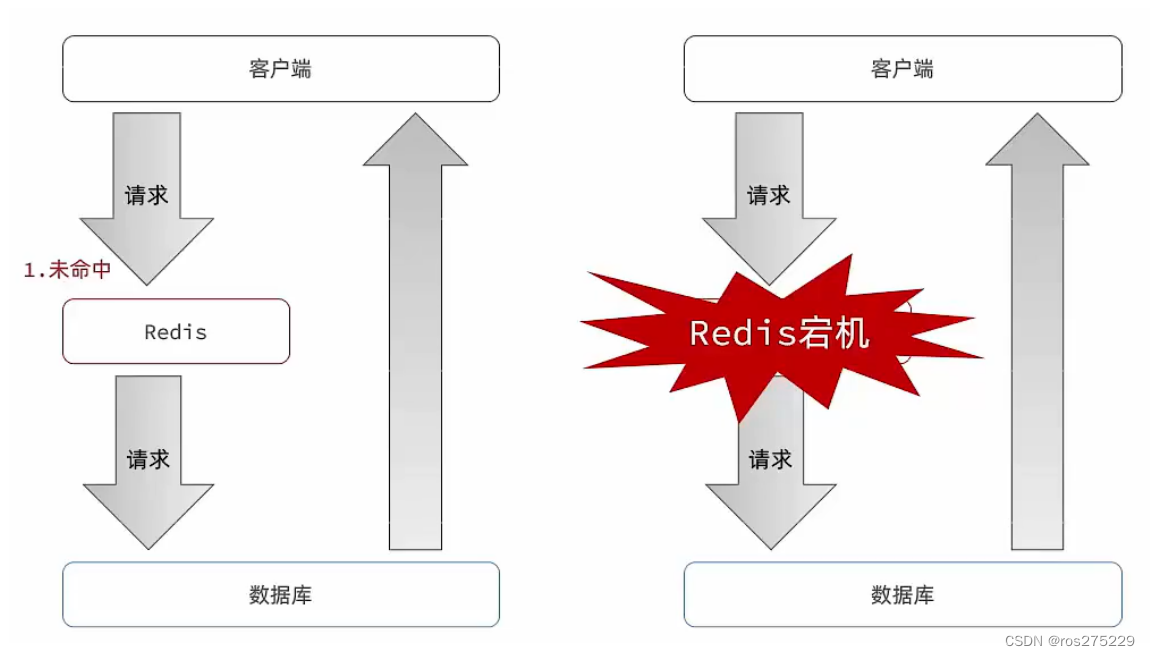
Redis -- 缓存雪崩问题
缓存雪崩是指在同一时段大量的缓存key同时失效或者Redis服务宕机,导致大量请求到达数据库,带来巨大压力。 可能原因 : 同一时间大量的key到期 ; 解决方案: 给不同的Key的TTL添加随机值 利用Redis集群提高服务的可用性 给缓存业务添加降…...

【ARM 嵌入式 C 文件操作系列 20 -- 文件删除函数 remove 详细介绍】
请阅读【嵌入式开发学习必备专栏 】 文章目录 文件删除函数 remove 文件删除函数 remove 在 C 语言中, 可以使用 remove 函数来删除一个文件,但在删除之前 可能想确认该文件是否存在。 可以使用 stat 函数来检查文件是否存在。 以下是如何实现这个功能…...
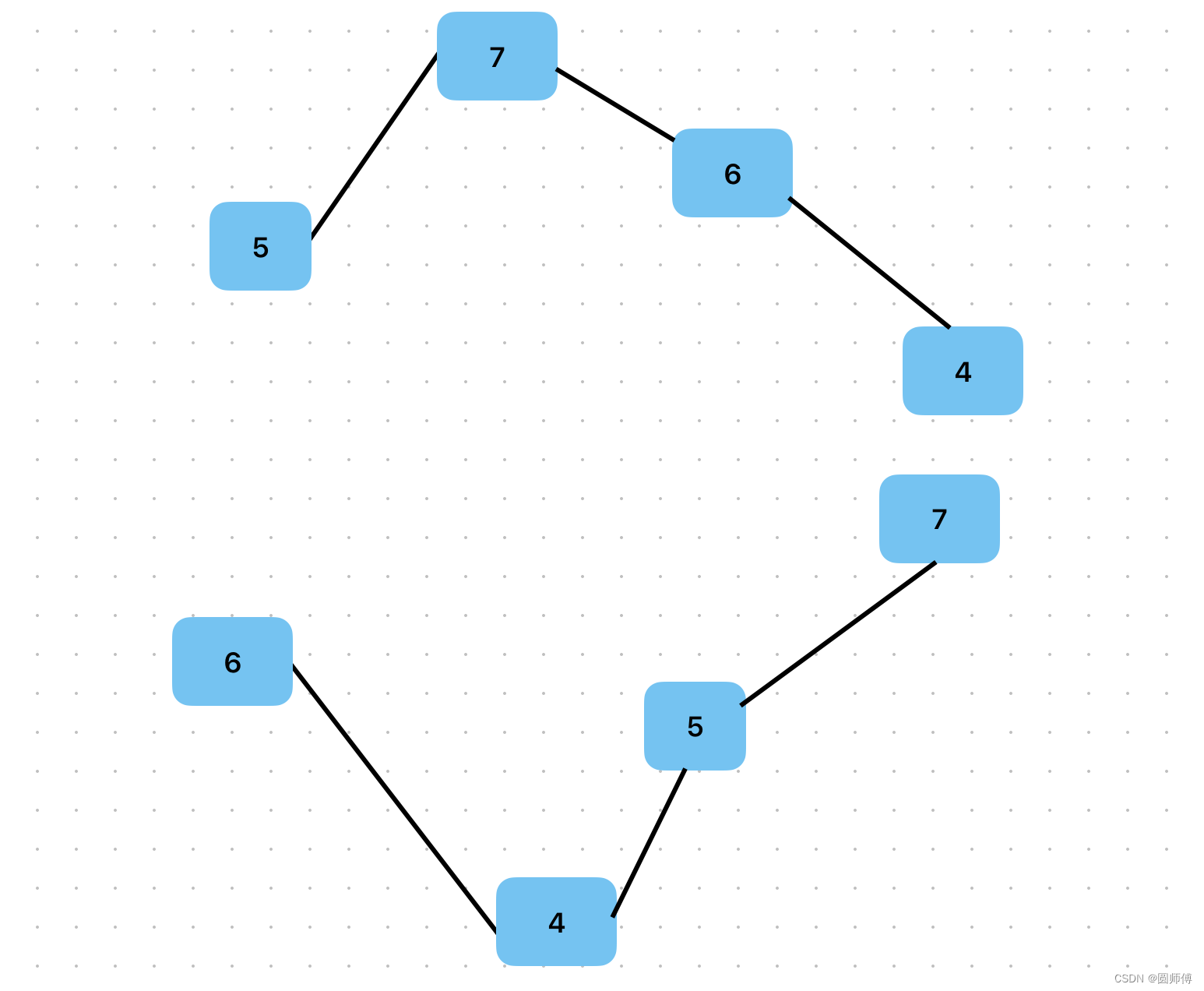
LeetCode刷题之31.下一个排列
文章目录 1. 题目2.分析3.解答3.1 先排序,后交换3.2 先交换,后排序 1. 题目 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3…...
- 向量定点算术指令)
【RISC-V 指令集】RISC-V 向量V扩展指令集介绍(九)- 向量定点算术指令
1. 引言 以下是《riscv-v-spec-1.0.pdf》文档的关键内容: 这是一份关于向量扩展的详细技术文档,内容覆盖了向量指令集的多个关键方面,如向量寄存器状态映射、向量指令格式、向量加载和存储操作、向量内存对齐约束、向量内存一致性模型、向量…...

【Java网络编程】IP网络协议与TCP、UDP网络传输层协议
1.1、IP协议 当应用层的数据被封装后,想要将数据在网络上传输,数据究竟要被发往何处,又该如何精准的在网络上定位目标机器,此时起到关键作用的就是“IP协议”。IP协议的作用在于把各种数据包准确无误的传递给目标方,其…...

C# 分布式自增ID算法snowflake(雪花算法)
文章目录 1. 概述2. 结构3. 代码3.1 IdWorker.cs3.2 IdWorkerTest.cs (测试) 1. 概述 分布式系统中,有一些需要使用全局唯一ID的场景,这种时候为了防止ID冲突可以使用36位的UUID,但是UUID有一些缺点,首先他相对比较长,…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
