NIUSHOP完美运营版商城 虚拟商品全功能商城 全能商城小程序 智慧商城系统 全品类百货商城
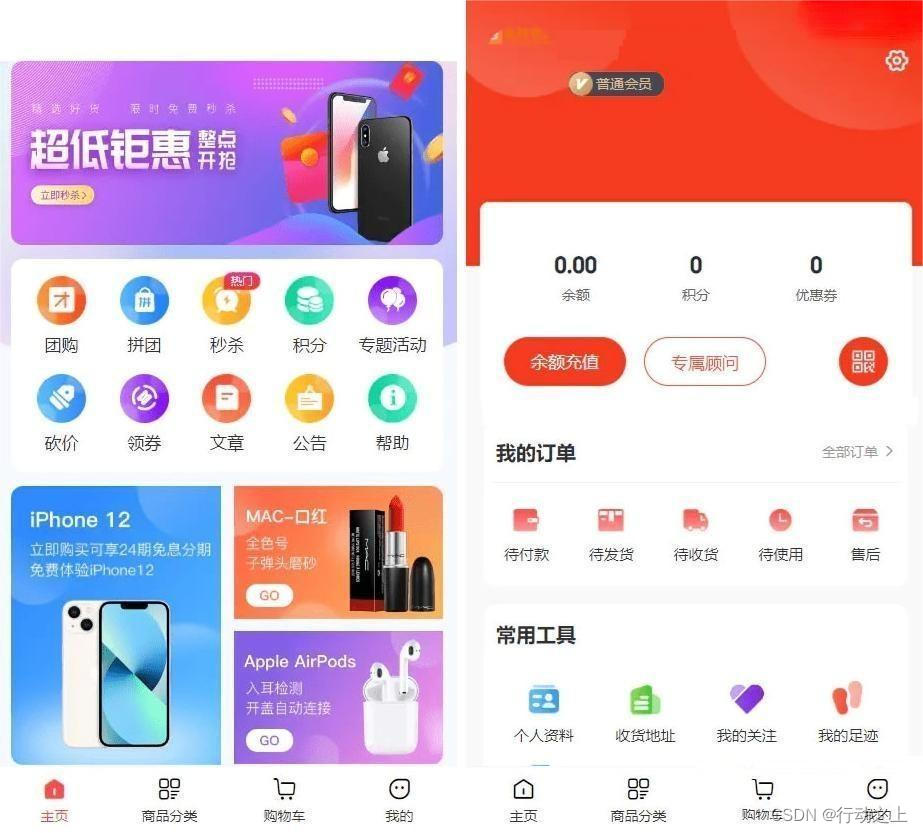
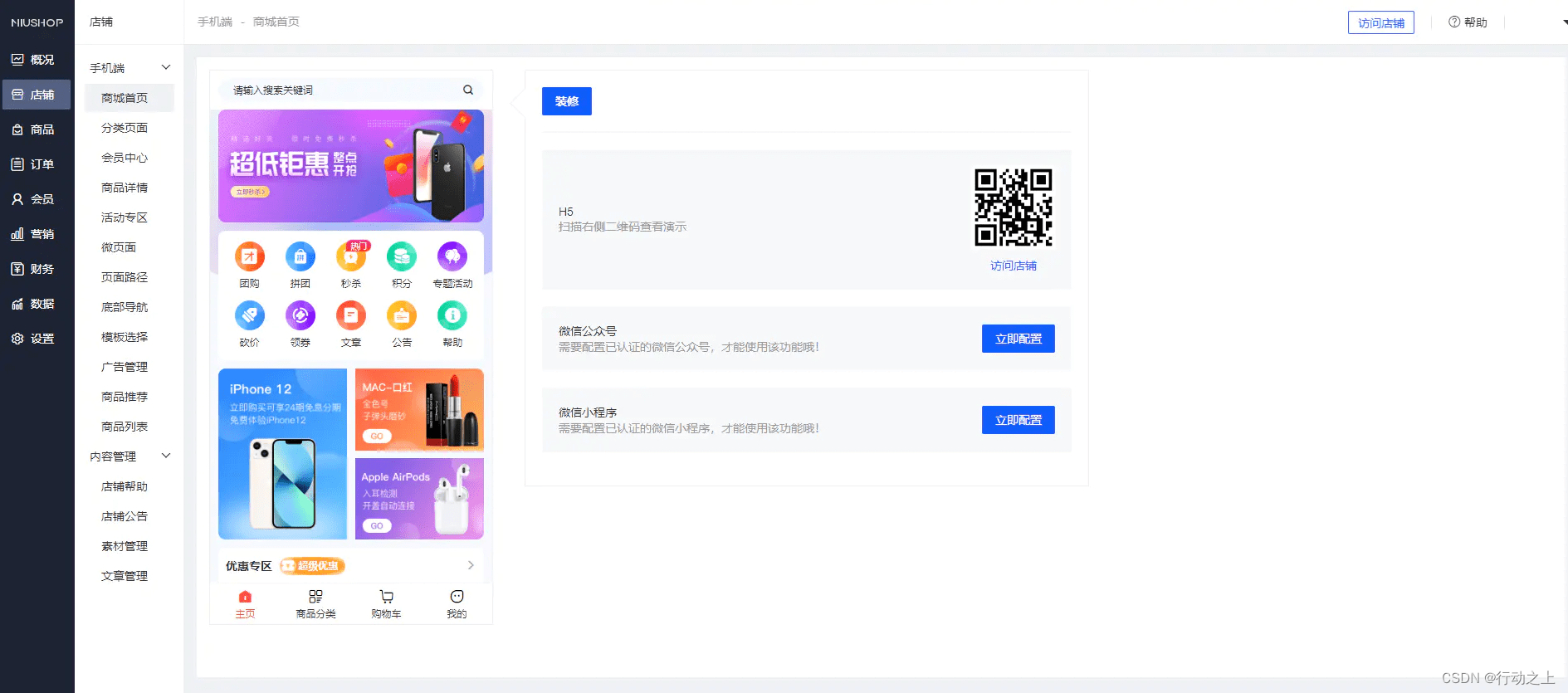


完美运营版商城/拼团/团购/秒杀/积分/砍价/实物商品/虚拟商品等全功能商城
干干净净 没有一丝多余收据 还没过手其他站 还没乱七八走的广告和后门
后台可以自由拖曳修改前端UI页面 还支持虚拟商品自动发货等功能 挺不错的一套源码
前端UNIAPP 后端PHP 一键部署版本
源码免费下载地址抄笔记 (chaobiji.cn)![]() https://chaobiji.cn/
https://chaobiji.cn/
相关文章:
NIUSHOP完美运营版商城 虚拟商品全功能商城 全能商城小程序 智慧商城系统 全品类百货商城
完美运营版商城/拼团/团购/秒杀/积分/砍价/实物商品/虚拟商品等全功能商城 干干净净 没有一丝多余收据 还没过手其他站 还没乱七八走的广告和后门 后台可以自由拖曳修改前端UI页面 还支持虚拟商品自动发货等功能 挺不错的一套源码 前端UNIAPP 后端PHP 一键部署版本 源码免费…...

vue2开发好还是vue3开发好vue3.0开发路线
Vue 2和Vue 3都是流行的前端框架,它们各自有一些特点和优势。选择Vue 2还是Vue 3进行开发,主要取决于你的项目需求、团队的技术栈、以及对新特性的需求等因素。以下是一些关于Vue 2和Vue 3的比较,帮助你做出决策: Vue 2࿱…...
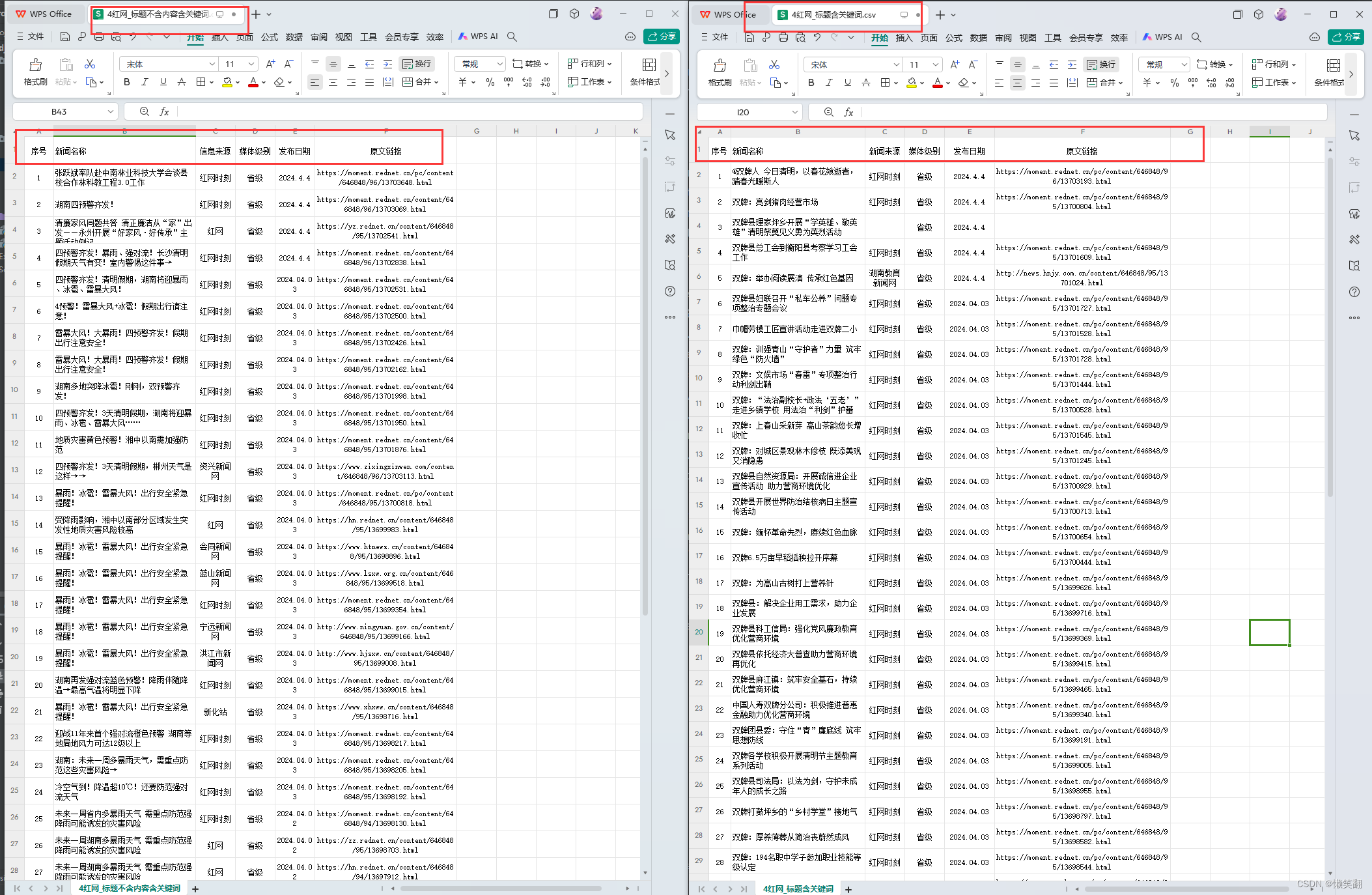
爬虫 新闻网站 并存储到CSV文件 以红网为例 V2.0 (控制台版)升级自定义查询关键词、时间段,详细注释
爬虫:红网网站, 获取指定关键词与指定时间范围内的新闻,并存储到CSV文件 V2.0(控制台版) 爬取目的:为了获取某一地区更全面的在红网已发布的宣传新闻稿,同时也让自己的工作更便捷 对比V1.0升级的…...
JavaSE-11笔记【多线程2(+2024新)】
文章目录 6.线程安全6.1 线程安全问题6.2 线程同步机制6.3 关于线程同步的面试题6.3.1 版本16.3.2 版本26.3.3 版本36.3.4 版本4 7.死锁7.1 多线程卖票问题 8.线程通信8.1 wait()和sleep的区别?8.2 两个线程交替输出8.3 三个线程交替输出8.4 线程通信-生产者和消费者…...

WebKit是什么?
WebKit是一个开源的浏览器引擎,它用于呈现网页内容在许多现代浏览器中,包括Safari浏览器、iOS内置浏览器、以及一些其他浏览器如Google Chrome的早期版本。以下是一些关于WebKit的重要信息: 起源和发展:WebKit最初是由苹果公司为其…...

谷歌(Google)历年编程真题——接雨水
谷歌历年面试真题——数组和字符串系列真题练习。 接雨水 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:…...

golang 归并回源策略
前言 下面是我根据业务需求画了一个架构图,没有特别之处,很普通,都是我们常见的中间件,都是一些幂等性GET 请求。有一个地方很有意思,从service 分别有10000 qps 请求到Redis,并且它们的key 是一样的。这样…...

【漏洞复现】可视化融合指挥调度平台 dispatch接口处存在任意文件上传漏洞
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...

最讨厌这种字符串问题了!!
题目:洛谷P1957口算练习题 题目大意描述: 第一行输入一个整数表示接下来要进行多少次运算,接下来每行输入一个字母c和两个数字x,y(输入的字母为a/b/c,分别表示要进行,-,*运算)或者就输入两个数…...
B-名牌赌王(本人遇到的题,做个笔记)
题解: #include <iostream> #include <queue> //需要用小根堆的优先队列 #include <unordered_map> //用无序映射 using namespace std; bool pai() {int n, m;cin >> n >> m; priority_queue<int, vector<int>, gr…...

博客评论回复03
接着之前写的,之前返回的数据集按道理来说渲染出来还是丑丑的,因此这次我看着抖音的评论样子,自己瞎写了一通,不过也算是模仿出来了虽然肯定没有抖音写的好。 类似与前面几章写的表结构 首先看看抖音评论区是怎么样的?…...
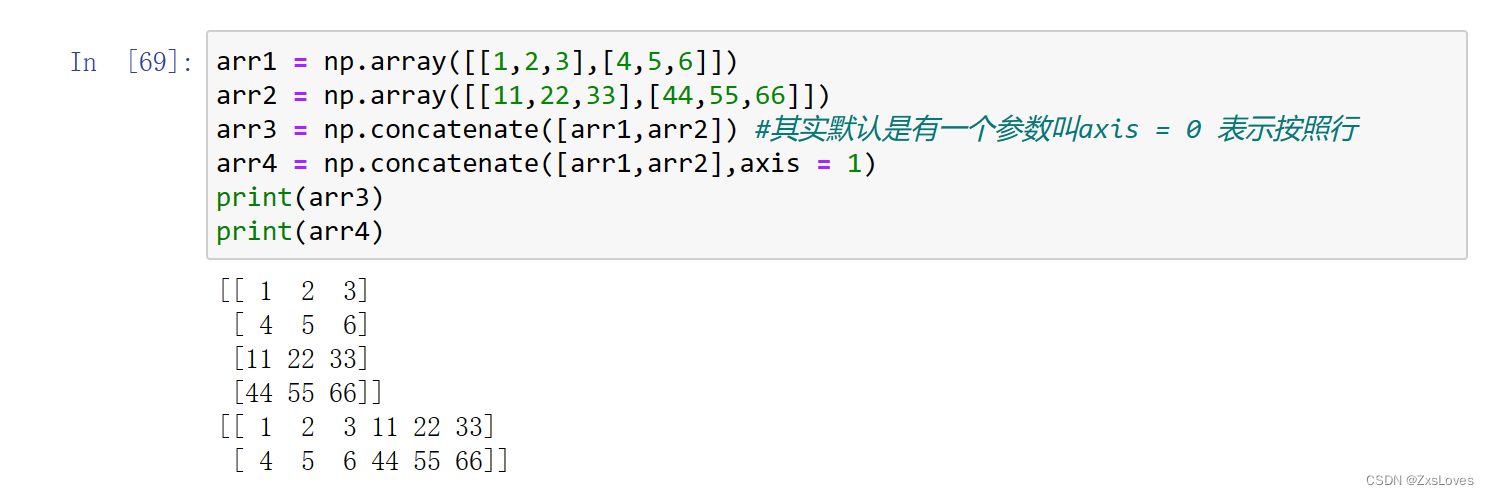
【【萌新的学习之Numpy数组的使用】】
萌新的学习之Numpy数组的使用 先记录一下之前的关于函数的设计 通过创造类的形式 复习完毕之后介绍numpy数组的使用 #整数型数组遇到除法 (即便是除以整数) 不同维度的数组之间 从外形上的本质区别 一维数组用1层中括号 二维数组用2层中括号 三维数…...
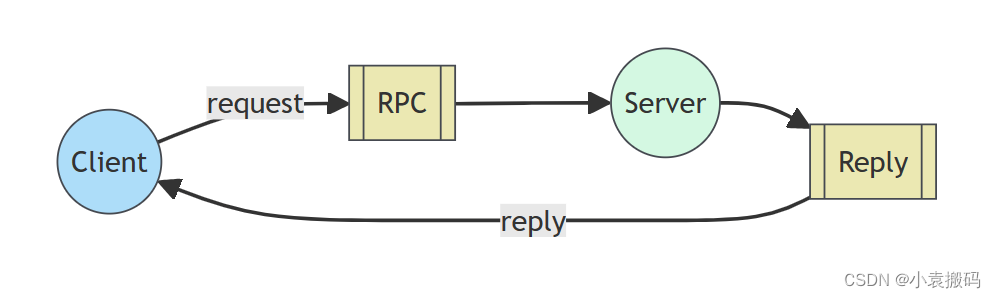
RabbitMQ3.13.x之七_RabbitMQ消息队列模型
RabbitMQ3.13.x之七_RabbitMQ消息队列模型 文章目录 RabbitMQ3.13.x之七_RabbitMQ消息队列模型1. RabbitMQ消息队列模型1. 简单队列2. Work Queues(工作队列)3. Publish/Subscribe(发布/订阅)4. Routing(路由)5. Topics(主题)6. RPC(远程过程调用)7. Publisher Confirms(发布者…...

Android JNI 调用第三方SO
最近一个项目使用了Go 编译了一个so库,但是这个so里面还需要使用第三方so库pdfium, 首先在Android工程把2个so库都放好 在jni中只能使用dlopen方式,其他的使用函数指针的方式来调用,和windows dll类似,不然虽然编译过了但是会崩溃…...
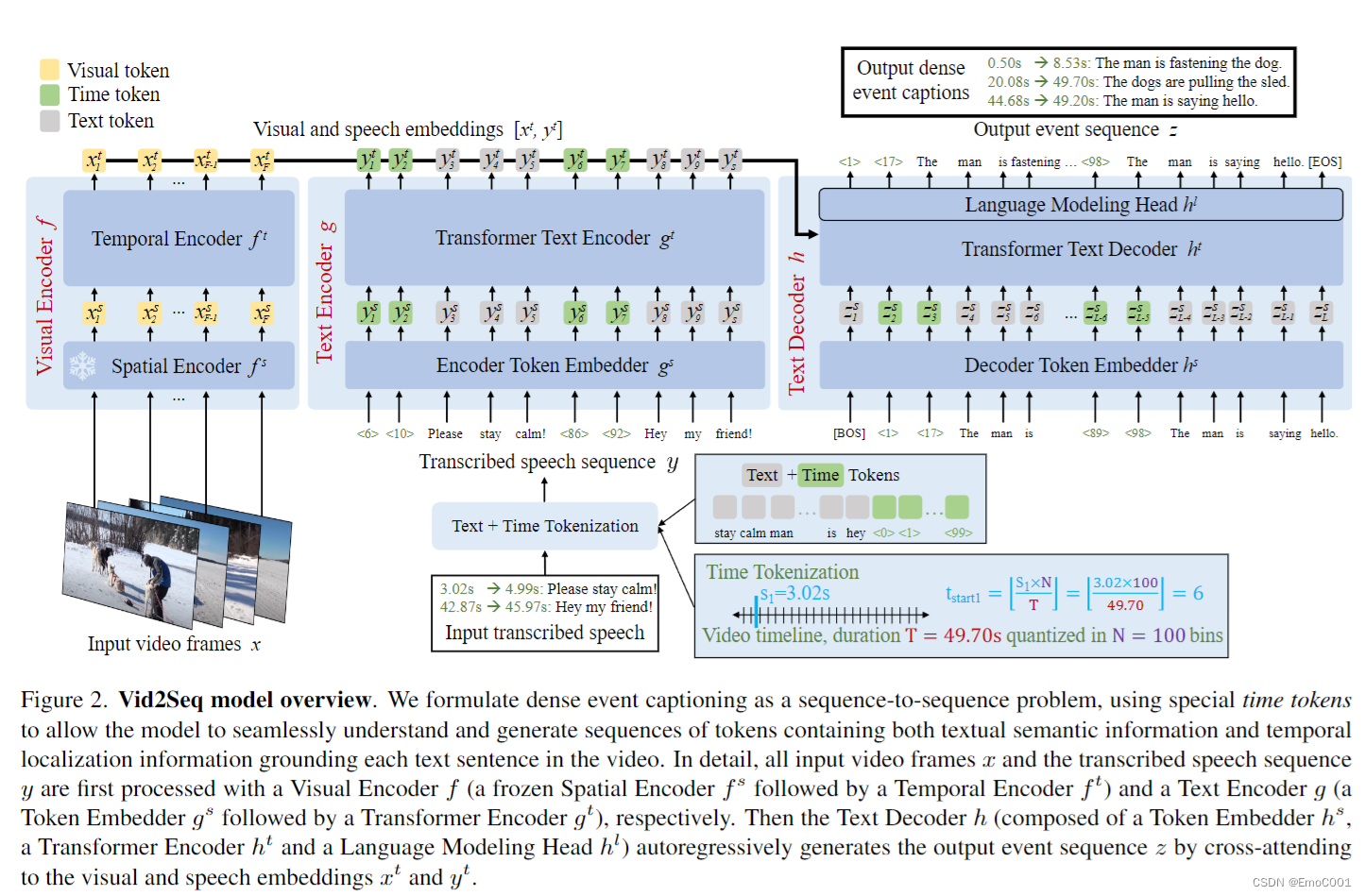
Vid2seq
Vid2Seq 应该是目前为止,个人最中意得一篇能够实际解决对一段视频进行粗略理解得paper了。个人认为它能够真正能解决视频理解是因为它是对一个模型整体做了训练,而不仅仅是通过visual encoders(e.g BLIP/CLIP/…)和 其它multi modal 的encoder直接过了个projection,做一个…...

Opencv人机交互界面设置
Opencv人机交互界面设置 以下是一些常见的OpenCV人机交互界面设置: 窗口交互 显示窗口:可以使用cv2.imshow()函数在屏幕上显示图像。例如,要显示名为“image”的图像,可以使用以下代码: import cv2img cv2.imread…...

蓝桥杯算法心得——字典树考试(贡献度+前缀和)
大家好,我是晴天学长,贡献度的题,找到技巧非常重要,需要的小伙伴可以关注支持一下哦!后续会继续更新的。💪💪💪 1) .字典树考试 字典树考试 问题描述 蓝桥学院最近教学了字典树这一数…...
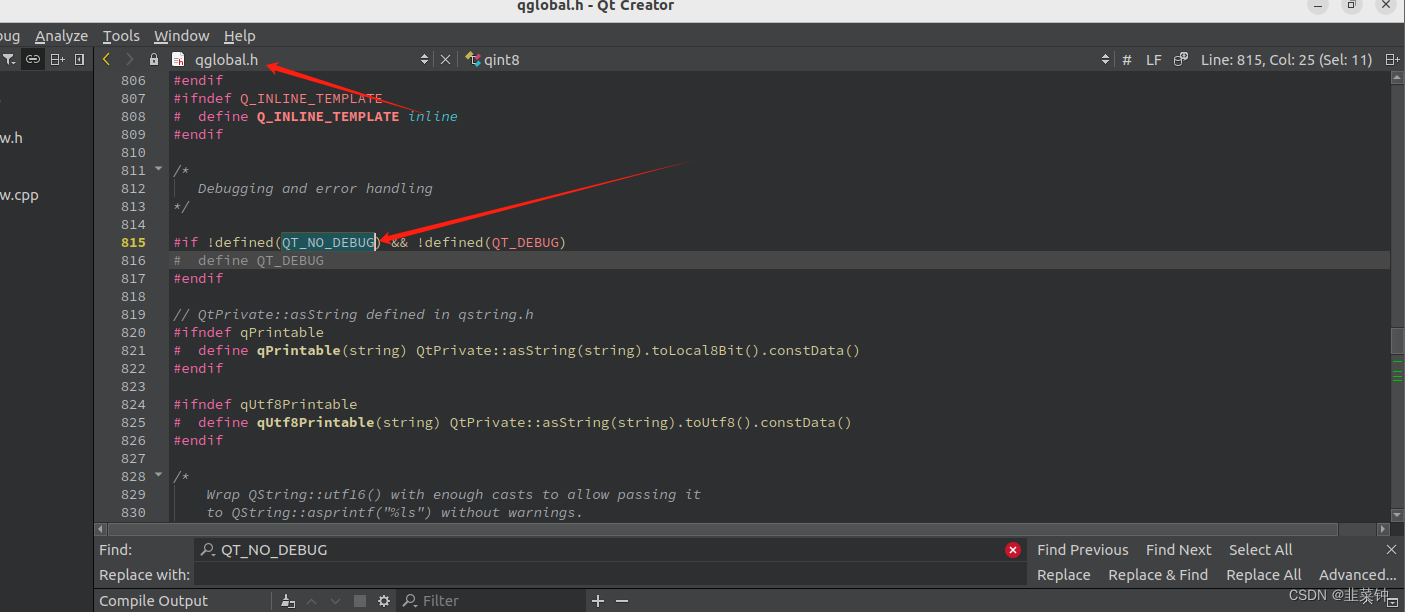
Linux下Qt生成程序崩溃文件
文章目录 1.背景2.Qt编译生成程序2.1.profile模式的本质 3.执行程序,得到core文件4.代码定位4.1.直接使用gdb4.2.使用QtCreator 5.总结6.题外话6.1.profile模式和debug模式的区别 1.背景 在使用Qt时,假如在windows,当软件崩溃时,…...

Go语言中测试和性能
1. 测试:软件开发最重要的方面 测试软件程序可能是软件开发人员能够做的最重要的事情。通过测试代码的功能,开发人员能够在很大程度上确定程序是有效的。另外,每次修改代码后,开发人员都可运行测试,确认没有引入Bug和衰退。通过测试软件,还能够让软件工程师确认程序按期望…...

回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测
回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测 目录 回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab基于CPO-GPR基于冠豪猪算法优化高斯…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
