蓝桥杯第十三届省赛C++B组(未完)
目录
刷题统计
修剪灌木
X进制减法
【前缀和+双指针】统计子矩阵
【DP】积木画
【图+DFS】扫雷
李白打酒加强版
DFS (通过64%,ACwing 3/11);
DFS(AC)
DP(AC)
砍竹子(X)
刷题统计
题目描述
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于 n 题?
输入格式
输入一行包含三个整数 a, b 和 n.
输出格式
输出一个整数代表天数。
样例输入
10 20 99
样例输出
8
提示
对于 50% 的评测用例,1 ≤ a, b, n ≤ 106 . 对于 100% 的评测用例,1 ≤ a, b, n ≤ 10^18 .
#include<iostream>
using namespace std;
typedef long long LL;
const int N=2e5+10,M=1e5+10;
int main(){int T=1;
// cin>>T;while(T--){LL a,b,n;cin>>a>>b>>n;LL t=a*5+b*2;LL ans=0;ans=n/t*7;n%=t;if(n>=a*5){ans+=5;n-=a*5;ans+=(n+b-1)/b;}else{ans+=(n+a-1)/a;}cout<<ans<<endl;}return 0;
}修剪灌木
题目描述
爱丽丝要完成一项修剪灌木的工作。有 N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木。当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。灌木每天从早上到傍晚会长高 1 厘米,而其余时间不会长高。在第一天的早晨,所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
输入格式
一个正整数 N ,含义如题面所述。
输出格式
输出 N 行,每行一个整数,第i行表示从左到右第 i 棵树最高能长到多高。
样例输入
3
样例输出
4 2 4
提示
对于 30% 的数据,N ≤ 10. 对于 100% 的数据,1 < N ≤ 10000.
#include<iostream>
using namespace std;
typedef long long LL;
const int N=2e5+10,M=1e5+10;
int a[10010];
int main(){int T=1;
// cin>>T;while(T--){int n;cin>>n;for(int i=1,j=n;i<=j;i++,j--){a[i]=a[j]=2*(n-i);}for(int i=1;i<=n;i++) cout<<a[i]<<endl;}return 0;
}X进制减法
题目描述
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制,因为其每一数位的进制并不固定!例如说某种 X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则 X 进制数 321 转换为十进制数为 65。
现在有两个 X 进制表示的整数 A 和 B,但是其具体每一数位的进制还不确定,只知道 A 和 B 是同一进制规则,且每一数位最高为 N 进制,最低为二进制。请你算出 A − B 的结果最小可能是多少。
请注意,你需要保证 A 和 B 在 X 进制下都是合法的,即每一数位上的数字要小于其进制。
输入格式
第一行一个正整数 N,含义如题面所述。
第二行一个正整数 Ma,表示 X 进制数 A 的位数。
第三行 Ma 个用空格分开的整数,表示 X 进制数 A 按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数 Mb,表示 X 进制数 B 的位数。
第五行 Mb 个用空格分开的整数,表示 X 进制数 B 按从高位到低位顺序各个数位上的数字在十进制下的表示。
请注意,输入中的所有数字都是十进制的。
输出格式
输出一行一个整数,表示 X 进制数 A − B 的结果的最小可能值转换为十进制后再模 1000000007 的结果。
样例输入
11 3 10 4 0 3 1 2 0
样例输出
94
提示
当进制为:最低位 2 进制,第二数位 5 进制,第三数位 11 进制时,减法得到的差最小。此时 A 在十进制下是 108,B 在十进制下是 14,差值是 94。
对于 30% 的数据,N ≤ 10; Ma, Mb ≤ 8. 对于 100% 的数据,2 ≤ N ≤ 1000; 1 ≤ Ma, Mb ≤ 100000; A ≥ B.
| 1 | 2 | 3 | |
| c(进制数组) | 11 | 5 | 2 |
| a | 10 | 4 | 0 |
A=(a1*c1+a2)*c3+a3;
#include<iostream>
using namespace std;
typedef long long LL;
const int N=1e5+10;
LL mod=1000000007;
LL a[N];
LL b[N];
LL c[N];
int main(){int T=1;
// cin>>T;while(T--){LL N;cin>>N;int ma;cin>>ma;for(int i=1;i<=ma;i++) cin>>a[i];int mb;cin>>mb;for(int i=1;i<=mb;i++) cin>>b[i];int k=ma,j=mb;for(k=ma,j=mb;k>=1&&j>=1;k--,j--){c[k]=max(a[k],b[j])+1;if(c[k]<2) c[k]=2;}while(k>=1){c[k]=max((LL)2,a[k]+1);k--;}LL A=a[1];for(int i=2;i<=ma;i++){A=(A*c[i]%mod+a[i])%mod;}LL B=b[1];j=ma-mb+2;for(int i=2;i<=mb;i++,j++){B=(B*c[j]%mod+b[i])%mod;}// cout<<A<<"---"<<B<<"---"<<endl;cout<<(A-B+mod)%mod<<endl;}return 0;
}【前缀和+双指针】统计子矩阵
给定一个 N × M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 × 1,最大 N × M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式:
第一行包含三个整数 N, M 和 K.
之后 N 行每行包含 M 个整数,代表矩阵 A.
输出格式
一个整数代表答案。
样例输入
3 4 10 1 2 3 4 5 6 7 8 9 10 11 12
样例输出
19
提示
满足条件的子矩阵一共有 19,包含:
大小为 1 × 1 的有 10 个。
大小为 1 × 2 的有 3 个。
大小为 1 × 3 的有 2 个。
大小为 1 × 4 的有 1 个。
大小为 2 × 1 的有 3 个。
对于 30% 的数据,N, M ≤ 20. 对于 70% 的数据,N, M ≤ 100.
对于 100% 的数据,1 ≤ N, M ≤ 500; 0 ≤ Ai j ≤ 1000; 1 ≤ K ≤ 250000000.
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=510;
LL w[N][N];
LL s[N][N];
int main(){int n,m,k;cin>>n>>m>>k;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>w[i][j];//每一列的前缀和(一维)s[i][j]=s[i-1][j]+w[i][j];}}LL sum=0,ans=0;//找j-i+1行,r-l+1列的子矩阵for(int i=1;i<=n;i++){//上边界for(int j=i;j<=n;j++){//下边界sum=0;for(int l=1,r=1;r<=m;r++){sum+=s[j][r]-s[i-1][r];while(l<=r&&sum>k){sum-=s[j][l]-s[i-1][l];l++;}ans+=r-l+1;}}}cout<<ans<<endl;//二维;
// int n,m,k;
// cin>>n>>m>>k;
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// cin>>w[i][j];
// s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+w[i][j];
// }
// }
// LL ans=0;
// for(int x1=1;x1<=n;x1++){
// for(int x2=x1;x2<=n;x2++){
// for(int y1=1,y2=1;y2<=m;y2++){
// while(y1<=y2&&s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]>k) y1++;
// ans+=y2-y1+1;
// }
// }
// }
// cout<<ans<<endl;return 0;
}【DP】积木画
题目描述
小明最近迷上了积木画,有这么两种类型的积木,分别为 I 型(大小为 2 个单位面积)和 L 型(大小为 3 个单位面积):
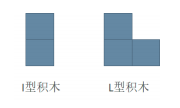
同时,小明有一块面积大小为 2 × N 的画布,画布由 2 × N 个 1 × 1 区域构成。小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式? 积木可以任意旋转,且画布的方向固定。
输入格式
输入一个整数 N,表示画布大小。
输出格式
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 取模后的值。
样例输入
3
样例输出
5
提示
五种情况如下图所示,颜色只是为了标识不同的积木:
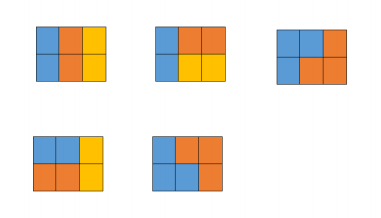
对于所有测试用例,1 ≤ N ≤ 10000000.
f[i][0]:表示第 i 列放满得方法数;
f[i][1]:表示第 i 列放满且第 i+1 列多一个得方案数。
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=1e7+10,mod=1000000007;
LL f[N][2];
int main(){int n;cin>>n;f[1][0]=1,f[1][1]=2,f[2][0]=2,f[2][1]=4;for(int i=3;i<=n;i++){f[i][0]=(f[i-1][0]+f[i-2][0]+f[i-2][1])%mod;f[i][1]=(f[i-1][1]+f[i-1][0]*2)%mod;}cout<<f[n][0]<<endl;return 0;
}【图+DFS】扫雷
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下, 在一个二维平面上放置着 n 个炸雷,第 i 个炸雷 (xi , yi ,ri) 表示在坐标 (xi , yi) 处存在一个炸雷,它的爆炸范围是以半径为 ri 的一个圆。
为了顺利通过这片土地,需要玩家进行排雷。玩家可以发射 m 个排雷火箭,小明已经规划好了每个排雷火箭的发射方向,第 j 个排雷火箭 (xj , yj ,rj) 表示这个排雷火箭将会在 (xj , yj) 处爆炸,它的爆炸范围是以半径为 rj 的一个圆,在其爆炸范围内的炸雷会被引爆。同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?
你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
输入格式
输入的第一行包含两个整数 n、m.
接下来的 n 行,每行三个整数 xi , yi ,ri,表示一个炸雷的信息。
再接下来的 m 行,每行三个整数 xj , yj ,rj,表示一个排雷火箭的信息。
输出格式
输出一个整数表示答案。
样例输入
2 1 2 2 4 4 4 2 0 0 5
样例输出
2
提示
示例图如下,排雷火箭 1 覆盖了炸雷 1,所以炸雷 1 被排除;炸雷 1 又覆盖了炸雷 2,所以炸雷 2 也被排除。
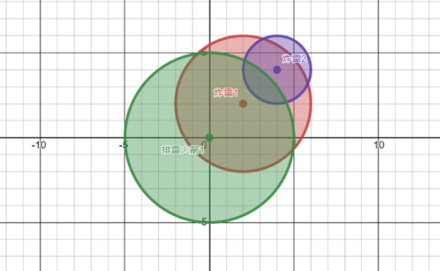
对于 40% 的评测用例:0 ≤ x, y ≤ 10^9 , 0 ≤ n, m ≤ 10^3 , 1 ≤ r ≤ 10.
对于 100% 的评测用例:0 ≤ x, y ≤ 10^9 , 0 ≤ n, m ≤ 5 × 10^4 , 1 ≤ r ≤ 10.
#include<iostream>
#include<algorithm>
#include<map>
#include<vector>
#define int long long
//typedef long long LL;
using namespace std;
const int N=5e4+10;
struct str{int x,y,r;int cnt;bool operator<(str const &m) const{if(x==m.x) return y<m.y;return x<m.x;}
}arr[N];
int n,m;
vector<int> e[N];
bool vis[N];
map<pair<int,int>,int>mp;
int get(int x1,int y1,int x2,int y2){return (x2-x1)*(x2-x1)+(y2-y1)*(y2-y1);
}
void add(int index){for(int i=index-1;i>=1;i--){if(arr[index].x-arr[index].r>arr[i].x) break;if(arr[index].r*arr[index].r>=get(arr[index].x,arr[index].y,arr[i].x,arr[i].y)){e[index].push_back(i);}}for(int i=index+1;i<=n;i++){if(arr[index].x+arr[index].r<arr[i].x) break;if(arr[index].r*arr[index].r>=get(arr[index].x,arr[index].y,arr[i].x,arr[i].y)){e[index].push_back(i);}}
}
int dfs_2(int index){vis[index]=1;int sum=arr[index].cnt;for(int i=0;i<e[index].size();i++){int t=e[index][i];if(!vis[t]) sum+=dfs_2(t);}return sum;
}
int dfs_1(int x,int y,int r){int cnt=0;str str1={x-r,y,r};str str2={x+r,y,r};int ll,rr;ll=lower_bound(arr+1,arr+n+1,str1)-arr;rr=lower_bound(arr+1,arr+n+1,str2)-arr;ll=min(ll,n),rr=min(rr,n);for(int i=ll;i<=rr;i++){if(i==0) continue;if(!vis[i]){if(r*r>=get(x,y,arr[i].x,arr[i].y)){cnt+=dfs_2(i);}}}return cnt;
}
signed main(){scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){int x,y,r;scanf("%lld%lld%lld",&x,&y,&r);int t=mp[{x,y}];if(t){arr[t].cnt++;arr[t].r=max(arr[t].r,r);}else{mp[{x,y}]=i;arr[i]={x,y,r,1};}}sort(arr+1,arr+n+1);for(int i=1;i<=n;i++){add(i);}int ans=0;for(int i=0;i<m;i++){int x,y,r;scanf("%lld%lld%lld",&x,&y,&r);ans+=dfs_1(x,y,r);}cout<<ans<<endl;return 0;
}李白打酒加强版
题目描述
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒 2 斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店 N 次,遇到花 M 次。已知最后一次遇到的是花, 他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
注意:壶里没酒 ( 0 斗) 时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的。
输入格式
第一行包含两个整数 N 和 M.
输出格式
输出一个整数表示答案。由于答案可能很大,输出模 1000000007 的结果。
样例输入
5 10
样例输出
14
提示
如果我们用 0 代表遇到花,1 代表遇到店,14 种顺序如下:
010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100
对于 40% 的评测用例:1 ≤ N, M ≤ 10。
对于 100% 的评测用例:1 ≤ N, M ≤ 100。
DFS (通过64%,ACwing 3/11);
#include<iostream>
using namespace std;
#define int long long
int mod=1000000007;
int n,m;
int ans=0;
void dfs(int cnt,int x,int y){if(cnt<0) return ;if(y==m+1){if(x==n+1&&cnt==0){ans++;ans%=mod;// cout<<cnt<<' '<<m-y<<"---"<<endl;}return ;}if(cnt>m-y+1||n-x>=m-y) return ;if(y>m+1||x>n+1) return ;dfs(cnt*2,x+1,y);dfs(cnt-1,x,y+1);
}
signed main(){scanf("%d%d",&n,&m);dfs(2,1,1);cout<<ans%mod<<endl;return 0;
}DFS(AC)
#include<iostream>
#include<cstring>
using namespace std;
#define int long long
const int N=110;
int mod=1000000007;
int n,m;
int ans=0;
int arr[N][N][N];
int dfs(int n,int m,int cnt){if(m<0||n<0) return 0;if(arr[n][m][cnt]!=-1) return arr[n][m][cnt];if(cnt<0) return 0;if(m==0){if(n==0&&cnt==0) return 1;return 0;}if(cnt>m||n>=m) return 0;ans=dfs(n-1,m,cnt*2)+dfs(n,m-1,cnt-1);ans%=mod;arr[n][m][cnt]=ans;return ans;
}
signed main(){memset(arr,-1,sizeof arr);scanf("%d%d",&n,&m);cout<<dfs(n,m,2)<<endl;return 0;
}DP(AC)
f[i][j][k]:走到了第i个位置,遇到了j个花,还剩k斗酒的合法方案数.
#include<iostream>
using namespace std;
#define int long long
const int N=110;
int f[N*2][N][N*2];
int mod=1000000007;
signed main(){int n,m;cin>>n>>m;f[0][0][2]=1;for(int i=1;i<n+m;i++){for(int j=0;j<m;j++){for(int k=0;k<=m;k++){//k为偶数,第i个可以是店,也可以是花,k为奇数,只能是花if(k%2==0){//店转移f[i][j][k]=(f[i][j][k]+f[i-1][j][k>>1])%mod;}//花转移if(j>=1) f[i][j][k]=(f[i][j][k]+f[i-1][j-1][k+1])%mod;}}}cout<<f[n+m-1][m-1][1]<<endl;return 0;
}砍竹子(X)
相关文章:

蓝桥杯第十三届省赛C++B组(未完)
目录 刷题统计 修剪灌木 X进制减法 【前缀和双指针】统计子矩阵 【DP】积木画 【图DFS】扫雷 李白打酒加强版 DFS (通过64%,ACwing 3/11); DFS(AC) DP(AC) 砍竹子(X) 刷题统计 题目描述 小明决定从下周一开始努力刷题准…...

编程生活day7--明明的随机数、6翻了、吃火锅
明明的随机数 题目描述 明明想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了N个1到1000之间的随机整数(N≤100),对于其中重复的数字,只保留一个,把其余相同的数…...
css酷炫边框
边框一 .leftClass {background: #000;/* -webkit-animation: twinkling 1s infinite ease-in-out; 1秒钟的开始结束都慢的无限次动画 */ } .leftClass::before {content: "";width: 104%;height: 102%;border-radius: 8px;background-image: linear-gradient(var(…...
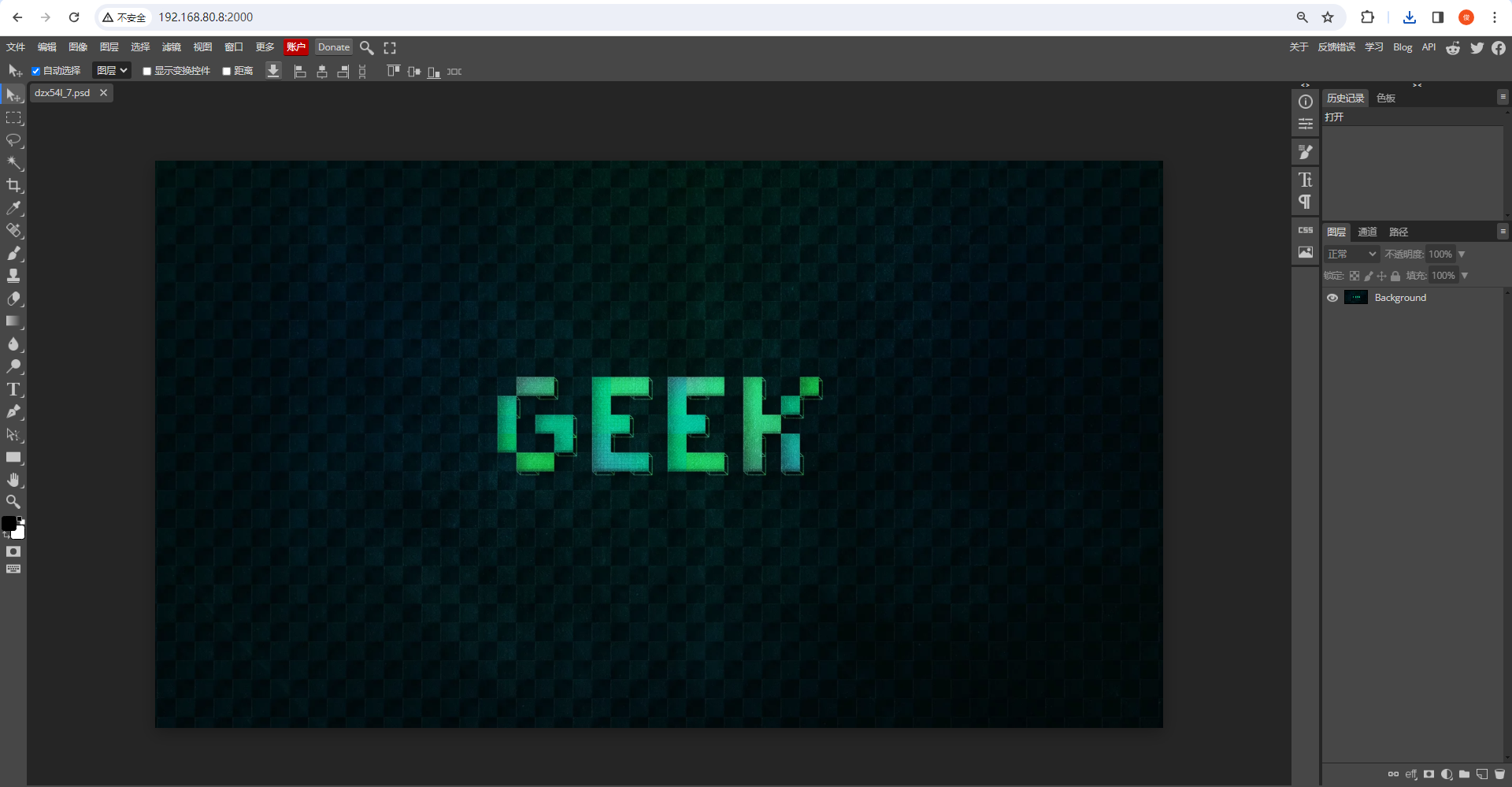
使用 Docker 部署 Photopea 在线 PS 工具
1)Photopea 介绍 GitHub:https://github.com/photopea/photopea 官方手册:https://www.photopea.com/learn/ Adobe 出品的「PhotoShop」想必大家都很熟悉啦,但是「PhotoShop」现在对电脑配置要求越来越高,体积越来越大…...

回溯法(一)——全排列 全组合 子集问题
全排列问题 数字序列 [ l , r ] [l,r] [l,r]区间内元素的全排列问题 extern int ans[],l,r,num;//num:方案数 extern bool flag[]; void dfs(int cl){//cl:current left,即为当前递归轮的首元素if(cl r 1){//数组已越界,本轮递归结束for…...
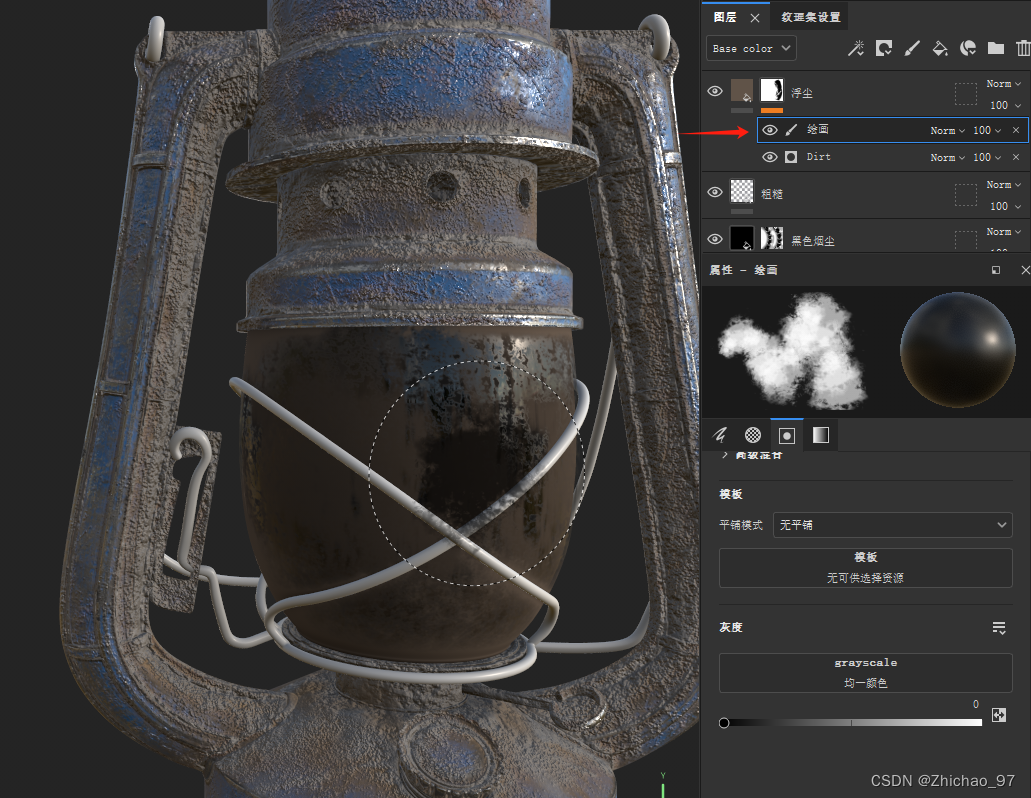
【Pt】马灯贴图绘制过程 04-玻璃脏迹
目录 效果 步骤 一、透明玻璃 二、烟熏痕迹 三、粗糙 四、浮尘 效果 步骤 一、透明玻璃 1. 打开纹理集设置,着色器链接选择“新的着色器链接” 在着色器设置中可以看到此时名称为“Main shader (Copy)” 这里修改名称为“玻璃” 在…...

Rust 程序设计语言学习——枚举模式匹配
枚举(enumerations),也被称作 enums。match 允许我们将一个值与一系列的模式相比较,并根据相匹配的模式执行相应代码。 1 枚举的定义 假设我们要跨省出行,有多种交通工具供选择。常用的交通工具有飞机、火车、汽车和轮…...

正则表达式(1)
文章目录 专栏导读1、match2、匹配目标3、通用匹配4、常用匹配规则表格 专栏导读 ✍ 作者简介:i阿极,CSDN 数据分析领域优质创作者,专注于分享python数据分析领域知识。 ✍ 本文录入于《python网络爬虫实战教学》,本专栏针对大学生…...

nginx + keepalived 搭建教程
1.安装依赖 yum install -y keepalived systemctl start keepalived systemctl enable keepalived 2.配置 a. keepalived.conf配置 global_defs {router_id nginx_server2 # 机器标识(backup节点为nfs_server2) }vrrp_script chk { script "/etc/keepalived/check_po…...

React事件和原生事件的执行顺序
在 React 中,事件处理分为两种类型:React 合成事件(Synthetic Event)和原生 DOM 事件(Native DOM Event)。它们的执行顺序略有不同。 React 合成事件 React 合成事件的执行顺序: React 合成事件…...

为什么在计算查询Q和键K的矩阵乘法时需要转置键矩阵K。示例说明q11,k11代表什么。线性变换矩阵 W_q 用于生成查询,W_k 用于生成键怎么获取的。
目录 为什么在计算查询Q和键K的矩阵乘法时需要转置键矩阵K。 示例说明q11,k11代表什么。...

剑指Offer题目笔记27(动态规划单序列问题)
面试题89: 问题: 输入一个数组表示某条街道上的一排房屋内财产的数量。相邻两栋房屋不能同时被盗,问小偷能偷取到的最多财物。 解决方案一(带缓存的递归): 解决方案: 由于有报警系统&…...

撸代码时,有哪些习惯一定要坚持?
我从2011年开始做单片机开发,一直保持以下撸代码的习惯。 1.做好代码版本管理 有些人,喜欢一个程序干到底,直到实现全部的产品功能,我以前做51单片机的项目就是这样。 如果功能比较多的产品,我不建议这样做࿰…...
)
【leetcode面试经典150题】17.罗马数字转整数(C++)
【leetcode面试经典150题】专栏系列将为准备暑期实习生以及秋招的同学们提高在面试时的经典面试算法题的思路和想法。本专栏将以一题多解和精简算法思路为主,题解使用C语言。(若有使用其他语言的同学也可了解题解思路,本质上语法内容一致&…...
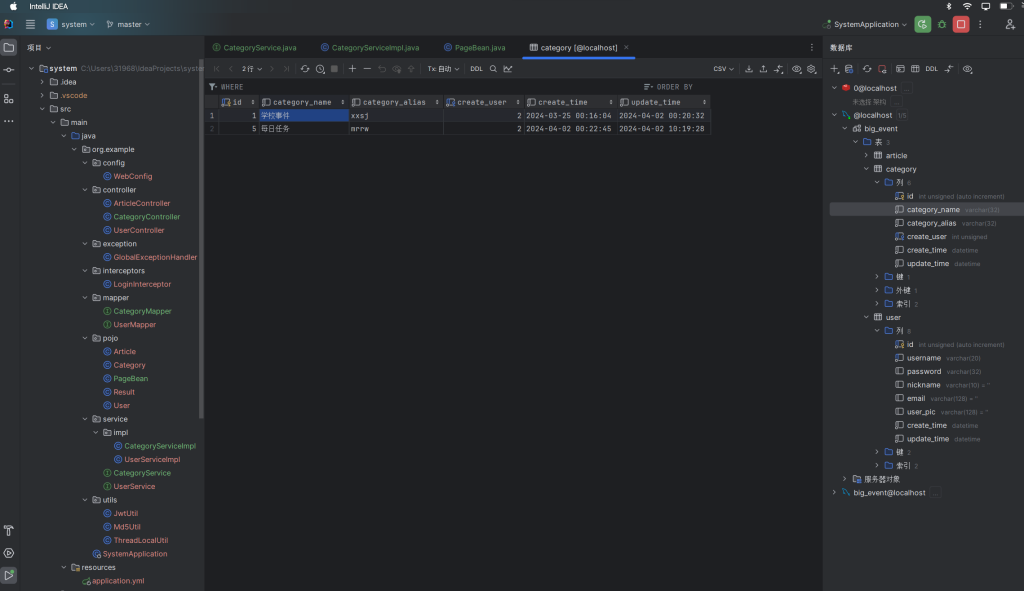
前后端开发之——文章分类管理
原文地址:前后端开发之——文章分类管理 - Pleasure的博客 下面是正文内容: 前言 上回书说到 文章管理系统之添加文章分类。就是通过点击“新建文章分类”按钮从而在服务端数据库中增加一个文章分类。 对于文章分类这个对象,增删改查属于配…...
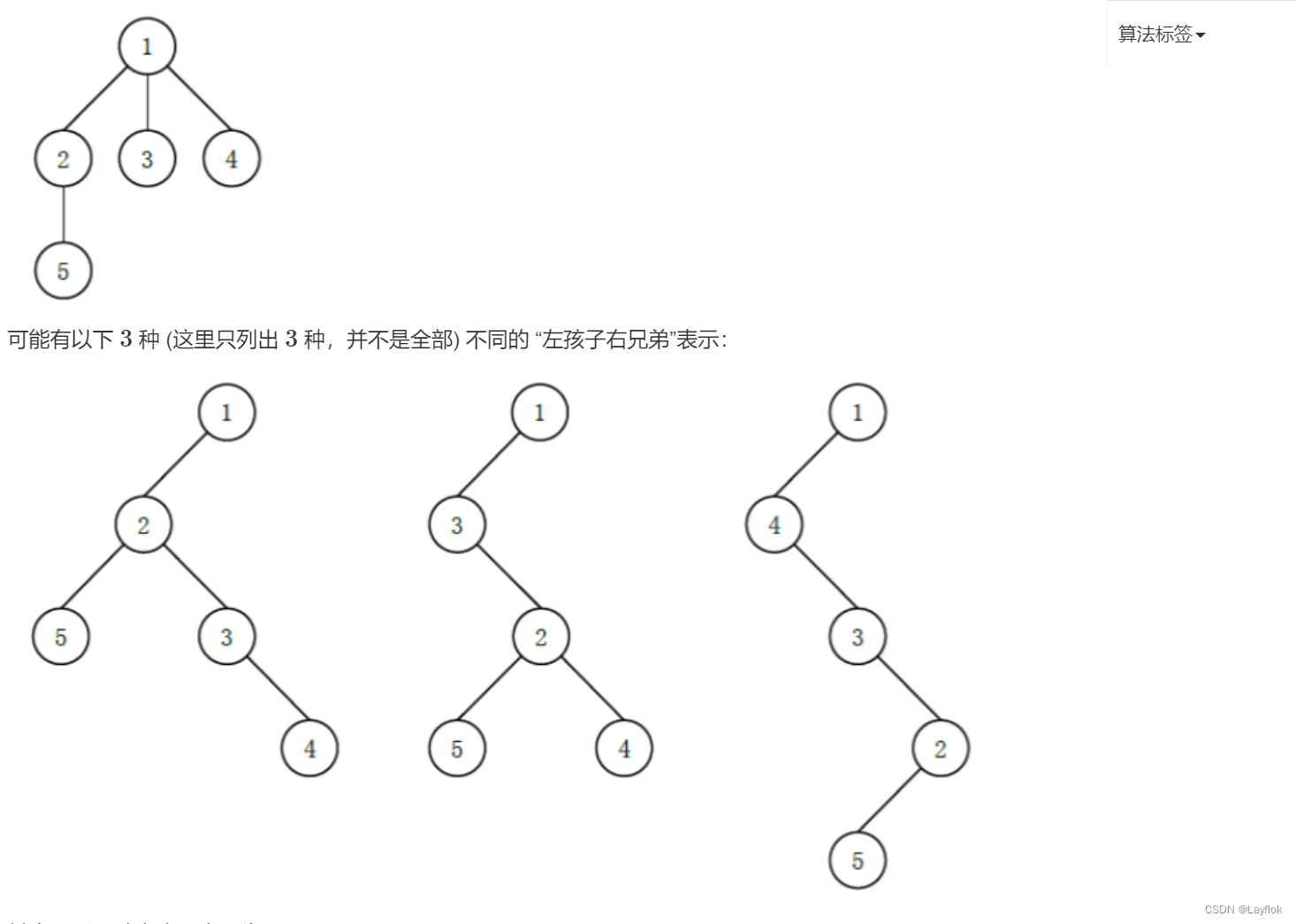
第12届蓝桥杯省赛 ---- C/C++ C组
文章目录 1. ASC2. 空间3. 卡片4. 相乘5. 路径6.时间显示7.最少砝码8. 杨辉三角形9. 左孩子右兄弟 第12届蓝桥杯省赛,C/C C组真题,第10题不是很清楚,题解不敢乱放😁😁😁 1. ASC 额。。。。 #include <i…...
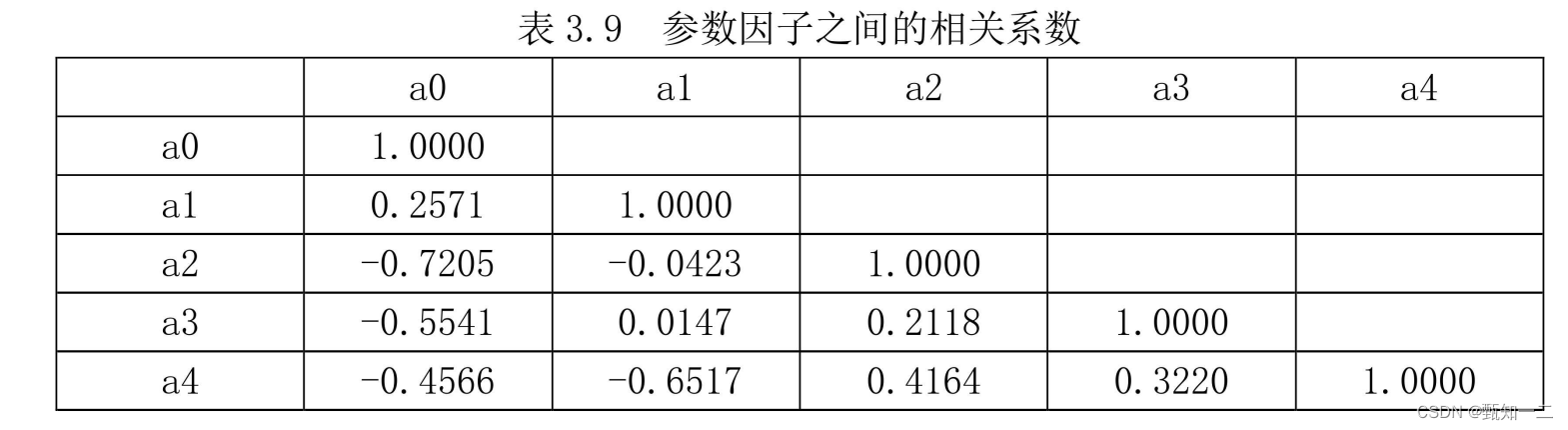
IVS模型解释
核心思路 【Implied volatility surface predictability: The case of commodity markets】 半参数化模型:利用各种参数(或者因子)对隐含波动率进行降维(静态参数化因子模型),对参数化因子的时间序列进行间接的建模 基于非对称…...

通用开发技能系列:Git
云原生学习路线导航页(持续更新中) 本文是 通用开发技能系列 文章,主要对编程通用技能Git进行学习 1.为什么使用版本控制系统 版本控制系统可以解决的问题 代码备份很重要版本控制很重要协同工作很重要责任追溯很重要 常见的版本控制系统 Gi…...
最新怎么订阅OnlyFans上喜欢的博主,详细教程
大家好,本文教大家如何用虚拟信用卡在 Onlyfans 订阅,链接在浏览器打开地址https://bewildcard.com/i/GPT310,虚拟卡开好之后,用支付宝充值就可以进行订阅OnlyFans平台的博主了。 什么是OnlyFans? OnlyFans 是一个提…...
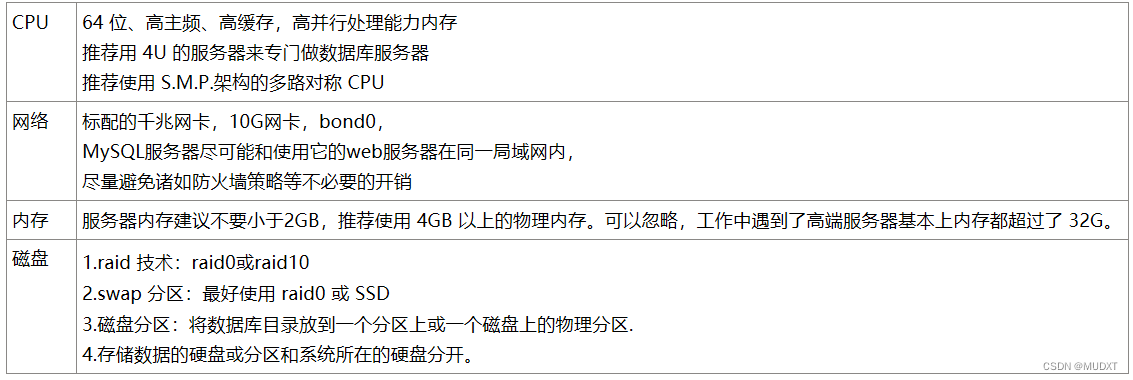
Mysql故障和优化
一、MySQL故障 二、MySQL优化 1.硬件优化: 2.数据库设计与规划 1.提前估计数据量,使用什么存储引擎 2.数据库服务器专机专用,避免额外的服务可能导致的性能下降和不稳定性 3.增加多台服务器,以达到稳定、高效的效果。主从同步、…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
