蓝桥杯23年第十四届省赛-异或和之和|拆位、贡献法
题目链接:
蓝桥杯2023年第十四届省赛真题-异或和之和 - C语言网 (dotcpp.com)
1.异或和之和 - 蓝桥云课 (lanqiao.cn)
参考题解:
蓝桥杯真题讲解:异或和之和 (拆位、贡献法)-CSDN博客
洛谷P9236 [蓝桥杯 2023 省 A] 异或和之和 题解_c加加区间异或问题洛谷ir-CSDN博客
说明:
1.需要知道一个重要的结论(图片来自参考题解):
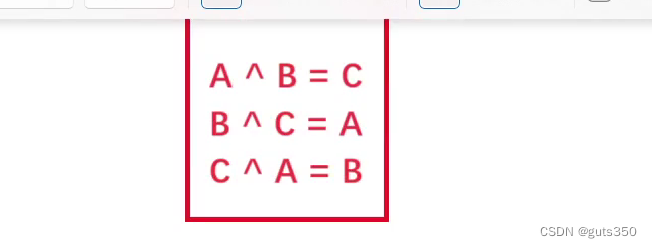
注:为什么A^B=C可以得到B^C=A ?在原式上两边同时异或上一个B,根据异或的性质,B^B=0,与0异或等于本身。
2.那么由前缀和可以得出
(sum(j,i)为i和j这个区间上面的异或和,右下角第二排的式子等号两边同时异或上一个s[j-1]得到第一排的式子):
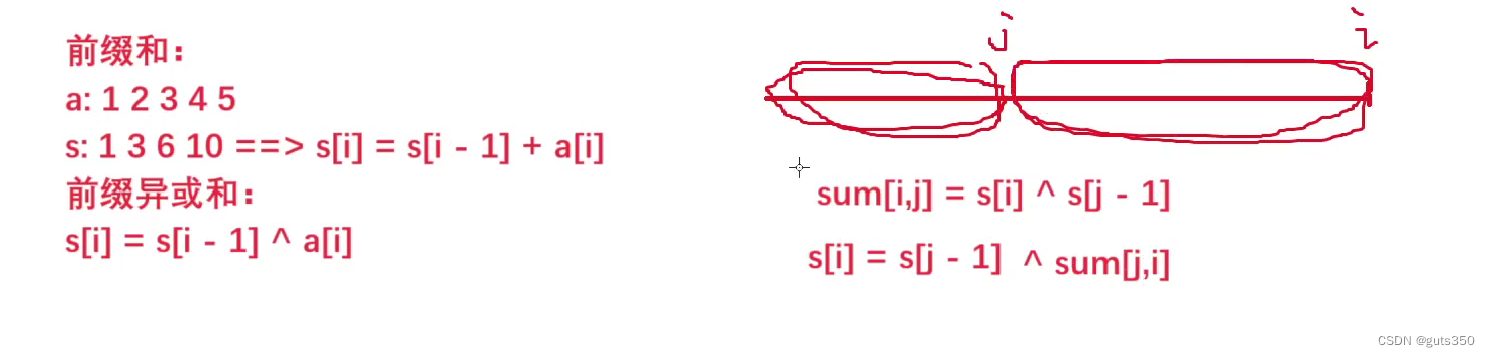
3.从推出的这个式子来看,sum[i,j]=s[i]^s[j-1],(i右端点,j左端点)
说明任意一个区间上面的异或和都可以转化成两个异或前缀和的异或和。再考虑到,对于一个二进制位来说,异或和结果为1的时候才会对结果有影响(贡献),而奇数个1异或为1,偶数个为0,对应到这里的两个数(前缀和)异或,那么就是一个前缀和为0,一个为1,那么把n个数都进行拆位,就可以 对每一个二进制位 做操作数是0或1(只有拆成二进制的0和1才能直接用前面的结论)的异或位运算。
于是统计,在第k位(从0开始数)上,n个数中对应前缀和为0、1的数量,记为n0,n1,那么最后在这一位上的对结果的贡献就是n0*n1* 。
这里注意:需要把S[0]考虑进来,左端点位置为1的时候计算区间需要s[0] ,而S[0]为0 ,所以0的初始数量为1
为什么会是n0 * n1 * ?因为n0是前缀和为0的数量,n1是前缀和为1的数量,我们在n0个位置里面选一个,再在n1个位置里选一个,他们计算出来的区间异或和sum(i,j)是为1的,且这个sum(i,j)不重复,因为你计数的0和1的位置是不重复的,那么计算出来的sum(i,j)的至少由一个端点跟别的sum不一样,那么n0*n1是sum(i,j)为1的个数,乘上这一位上的基数即可。
4.另一种思路:
在参考题解第二个文章里,提出了另一种思路,既然
对于一个二进制位来说,异或和结果为1的时候才会对结果有影响(贡献),而奇数个1异或为1,偶数个为0
那么我统计我当前位置是出现1的奇数次还是偶数次,根据
sum[i,j]=s[i]^s[j-1]
为奇数次,s[i]为1,要求s[j-1]为偶数次;
为偶数次,s[i]为0,要求s[j-1]为奇数次(即要求总的次数为奇数)。
于是很容易去找(记前面为偶数次的 位置数 为 even,奇数次为odd):
s[i]为奇数次,是不是就有 even+1个 为奇数次1 的区间?(因为这even个偶数次的 位置都可以作为s[j-1]的这个j-1位置,还有s[0]=0,0也是偶数次,这个没被计数到,(1,i)也是一个奇数个的区间,所以还要加1)
s[i]为偶数次,是不是就有 odd个 为奇数次1 的区间,因为是要求s[j-1]为奇数次,所以不加1.
或者可以这样考虑:
s[i]为奇数次,even个前面为偶数次的 位置,这些位置第一次出现对应的数肯定是1,且这个1只出现一次(对应这个偶数),否则1的数量就变了,0可以出现无数次,那么就是对应一个偶数o,他出现的第一个位置m,a[m](假设a为第k位上,这n个数的01序列的数组名)为1,s[m-1]肯定只出现了o-1次,这个位置不能组成合法区间,去掉。
而对于一个奇数p,第一次出现的位置r,a[r]为1,s[r-1]为偶数次p-1,需要加上这个位置。
于是合法的区间=even-出现的偶数的数量(若出现2,4,则数量为2)+出现的奇数的数量
当s[i]为奇数次,奇数的数量比偶数数量多1,推出上面同样的式子。
s[i]为偶数次,二者相等,推出上面同样的式子。
5.注意:
数据范围,数组每个数小于等于2的20次方,那么要考虑的二进制位数就是21位,不是20位!!
代码:
仅异或前缀和
要枚举左右端点,时间复杂度 ,会超时。60%数据。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int ans=0;
int a[N];
int s[N];//异或前缀和 //vector<int> num[N];
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];//ans+=a[i];s[i]=s[i-1]^a[i];}for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){int sum=s[j]^s[i-1];// sum(i,j)^s[i-1]=s[j]两百年同时异或s[i-1]消掉左边的 s[i-1]ans+=sum;}}cout<<ans;return 0;
}说明3对应代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int ans=0;
int a[N];
int s[N];
//异或前缀和
int odd,even,cnt=0,radix=1;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i]; }radix=1;for(int i=0;i<=20;i++){//这里同样注意:需要把S[0]考虑进来,左端点位置为1的时候计算区间需要s[0] ,而S[0]为0 //所以0的初始数量为1 int n0=1,n1=0;for(int j=1;j<=n;j++){//求第i位上的二进制前缀和 s[j]=s[j-1]^(a[j]&1);if(s[j]==1){n1++;} else{n0++;}a[j]=a[j]>>1;}ans+=n0*n1*radix;radix=radix<<1;}cout<<ans;return 0;
}
说明4对应代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int ans=0;
int a[N];
int s[N];
//异或前缀和
int odd,even,cnt=0,radix=1;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}// 对二进制的21个位置中的第j个位置算n个数的贡献 //注意:是 0-20位!!!有21个位置 for(int j=0;j<=20;j++){cnt=0;odd=0,even=0;//对第i个数而言,它的二进制形式的第j位(从0开始数),能找到的能贡献1的区间数,//这个区间是i和前i个数组成的。有多少个能贡献1的区间在第i位上结果就加上多少个1 (最后结果要乘上第j位对应的基数:2的j次方) for(int i=1;i<=n;i++){//对n个数计算第j位上的异或和之和 //注意:取出最后一位的方法 int tt=a[i]&1;//取出二进制位 if(tt==1){//计算二进制第j位上,到第i个数是出现了几个1,用前缀和累加可以在O(1)复杂度计算出 s[i]=s[i-1]+1;}else{s[i]=s[i-1];}if(s[i]%2==0){//到第i数出现了偶数个1,那么他能找到 前i项中为奇数次的数量 个贡献1的区间 even++;ans+=(odd)*radix;//注意乘上第j位对应的基数 }else{//到第i数出现了奇数个1,那么他能找到 前i项中为偶数次的数量+1 个贡献1的区间 odd++;ans+=(even+1)*radix;}a[i]=a[i]>>1;//第i个数左移一位,方便下一次取j+1位 }radix=radix<<1;//j+1位,基数变成原来的2倍 }// for(int i=1;i<=n;i++){
// for(int j=i;j<=n;j++){
// int sum=s[j]^s[i-1];// sum(i,j)^s[i-1]=s[j]两百年同时异或s[i-1]消掉左边的 s[i-1]
// ans+=sum;
// }
// }cout<<ans;return 0;
}相关文章:
蓝桥杯23年第十四届省赛-异或和之和|拆位、贡献法
题目链接: 蓝桥杯2023年第十四届省赛真题-异或和之和 - C语言网 (dotcpp.com) 1.异或和之和 - 蓝桥云课 (lanqiao.cn) 参考题解: 蓝桥杯真题讲解:异或和之和 (拆位、贡献法)-CSDN博客 洛谷P9236 [蓝桥杯 2023 省 A]…...
回顾与思考)
Unity进阶之路(1)回顾与思考
首先呢,博主在这里先反思一下自己这几个月,其实并没有多少进步。 在寒假中,博主几乎是独立编写了一个小程序的完整UI和一个Uniapp的雏形。那段时间是博主生产力最高的时间段。几乎是每天8点起来开始编写代码,晚上一直忙到很晚。 …...
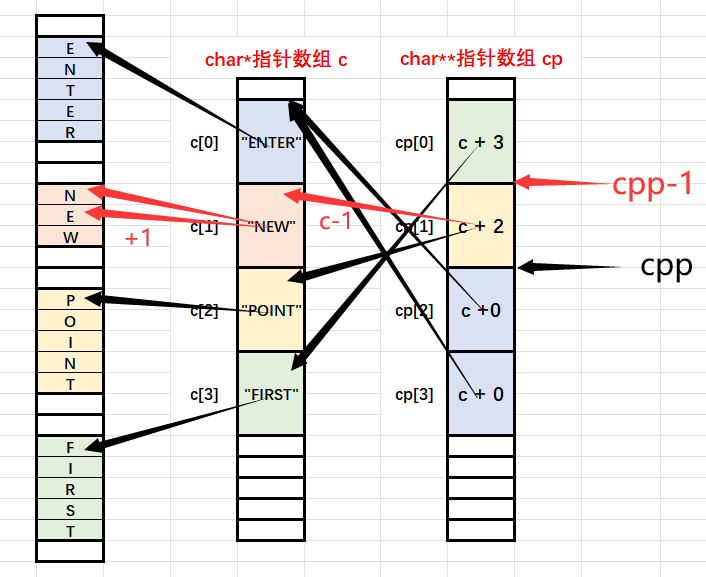
【C语言】——指针八:指针运算笔试题解析
【C语言】——指针八:指针运算笔试题解析 一、题一二、题二三、题三四、题四五、题五六、题六七、题七 一、题一 //程序输出结果是什么 int main() {int a[5] { 1,2,3,4,5 };int* ptr (int*)(&a 1);printf("%d, %d", *(a 1), *(ptr - 1));return…...
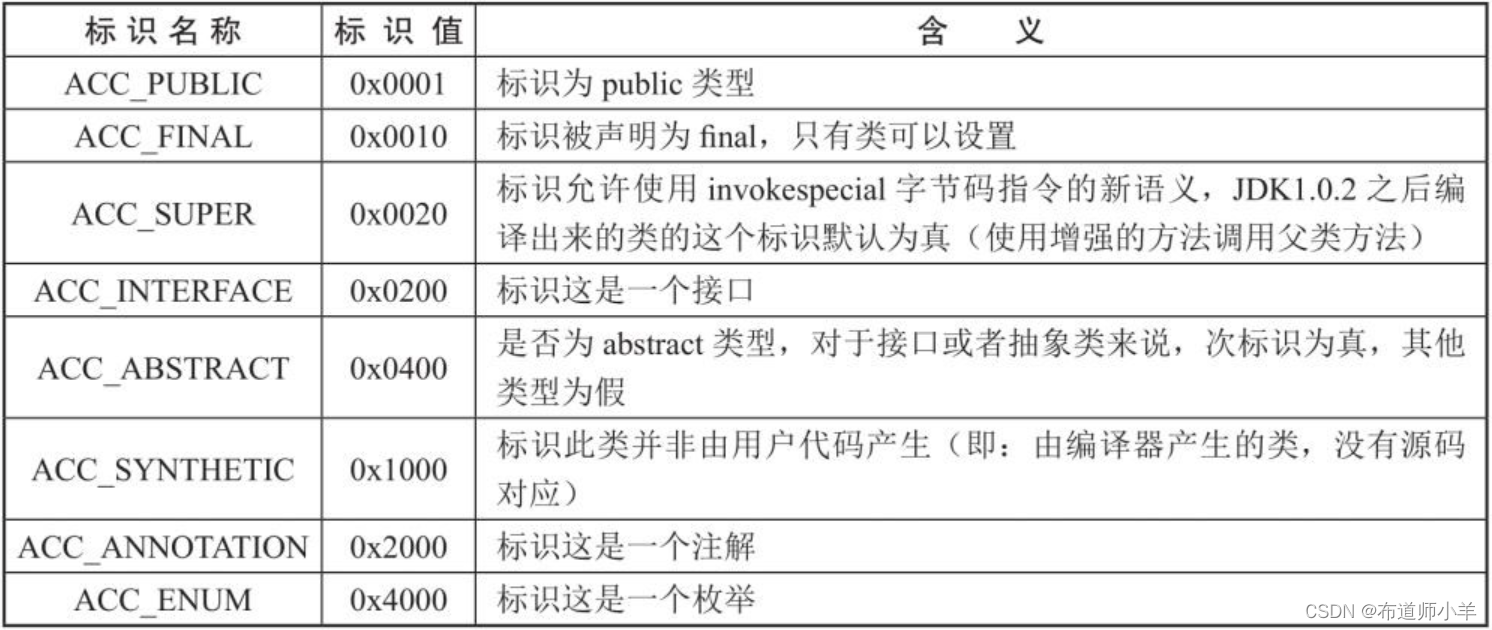
JVM字节码与类的加载——class文件结构
文章目录 1、概述1.1、class文件的跨平台性1.2、编译器分类1.3、透过字节码指令看代码细节 2、虚拟机的基石:class文件2.1、字节码指令2.2、解读字节码方式 3、class文件结构3.1、魔数:class文件的标识3.2、class文件版本号3.3、常量池:存放所…...
小程序如何通过公众号发送新订单提醒
当客户在小程序上下单后,公众号会发送订单通知,这可以让管理员及时获知用户下单情况,方便及时处理订单和提供服务。下面是具体介绍如何设置公众号来发送订单服务通知。 方式一:通过采云公众号发送订单通知 此种方式是默认的通知…...

聊聊公众号最让我不爽的两个痛点
本文首发于 Python猫 微信公众号最让我不爽的地方有两个,而且有很多人虽然也不爽,却不知道原因。 本文想聊聊公众号的两个痛点,因为我经常收到私信问这两个问题,本文算是一次集中的回复吧。 第一个不爽的点是公众号会屏蔽外链&…...

【leetCode】2810. 故障键盘
文章目录 [2810. 故障键盘](https://leetcode.cn/problems/faulty-keyboard/)思路一:模拟代码:思路二:双端队列代码: 2810. 故障键盘 思路一:模拟 用StringBuilder来拼贴字符遍历字符串,如果遇到i,对拼贴好…...

xshell7连接ubuntu18.04
🎡导航小助手🎡 1.查看ubuntu IP2.开启openssh-server3.静态IP设置4.Xshell连接 1.查看ubuntu IP 输入下面命令查看IP ifconfig -a可以看到网卡是ens33,IP为192.168.3.180。 2.开启openssh-server 1、执行下句,下载SSH服务 s…...

真正的力量:实力与人际关系的平衡艺术
在当今社会,人们常常在追求个人发展和建立良好人际关系之间寻找平衡。有一种观点认为,“没有实力,就不要对别人好。不然,很容易被定义为讨好。”这句话在一定程度上揭示了实力与人际关系之间的微妙联系。本文将探讨这一观点的深层…...

Acwing.1388 游戏(区间DP对抗思想)
题目 玩家一和玩家二共同玩一个小游戏。 给定一个包含 N个正整数的序列。 由玩家一开始,双方交替行动。 每次行动可以在数列的两端之中任选一个数字将其取走,并给自己增加相应数字的分数。(双初始分都是 0分) 当所有数字都被…...

Numpy数组转换为csv文件
参考:Converting Numpy Array to CSV 在数据分析和处理中,经常会涉及到将数据从一个形式转换为另一个形式的操作。 其中,将Numpy数组转换为csv文件是一种常见的操作,因为csv文件是一种通用的数据存储格式,方便与其他软…...
 ))
替代安全指标(Surrogate Safety Measures (SSM) )
替代安全措施(Surrogate Safety Measures (SSM) )用于从数据中寻找接近碰撞,或可能发生(但实际没有发生)的碰撞事件。 SSM的两个合格标准: (1)它应该来自与碰撞直接相关的交通冲突&…...

usb_camera传输视频流编码的问题记录!
前言: 大家好,今天给大家分享的内容是,一个vip课程付费的朋友,在学习过程中遇到了一个usb采集的视频数据流,经过ffmpeg编码,出现了问题: 问题分析: 其实这个问题不难,关键…...

Linux安装nginx保姆级教程
文章目录 前言一、nginx安装(保姆级教程)1.安装nginx依赖2.安装wget3.创建nginx安装目录4.下载nginx5.查看下载好的nginx6.解压缩7.查看当前目录下的文件→进入nginx-1.8.0目录→查看当前目录下的文件8.安装nginx9.查看nginx安装目录并启动nginx10.网络请…...
leetcode-判断二分图
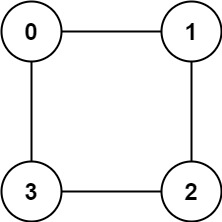
. - 力扣(LeetCode) 存在一个 无向图 ,图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,…...

算法day30 回溯6
332 重新安排行程 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。 所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK …...

分享three.js实现乐高小汽车
前言 Web脚本语言JavaScript入门容易,但是想要熟练掌握却需要几年的学习与实践,还要在弱类型开发语言中习惯于使用模块来构建你的代码,就像小时候玩的乐高积木一样。 应用程序的模块化理念,通过将实现隐藏在一个简单的接口后面&a…...

gpt的构造和原理
gpt是序列预测模型。 问答是通过确定问答格式样本训练出来的!比如“Q:xxxx.A:xxx"本质还是根据前面的序列预测后面的序列。在自回归训练过程中,文本序列(可能包含问题和紧随其后的答案)被视为一个整体输入到模型…...
基于springboot实现教师人事档案管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现IT技术交流和分享平台系统演示 摘要 我国科学技术的不断发展,计算机的应用日渐成熟,其强大的功能给人们留下深刻的印象,它已经应用到了人类社会的各个层次的领域,发挥着重要的不可替换的作用。信息管理作为计算…...

K8S之Job和CronJob控制器
这里写目录标题 Job概念适用场景使用案例 CronJob概念适用场景使用案例 Job 概念 Job控制器用于管理Pod对象运行一次性任务,例如:对数据库备份,可以直接在k8s上启动一个mysqldump备份程序,也可以启动一个pod,这个pod…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
