力扣每日一题:LCR112--矩阵中的最长递增路径
题目
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
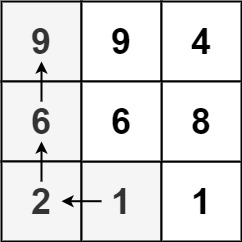
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
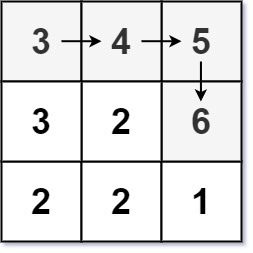
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]] 输出:1
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 231 - 1
注意:本题与主站 329 题相同: . - 力扣(LeetCode)
请问您在哪类招聘中遇到此题?
1/5
社招
校招
实习
未遇到
通过次数
16.3K
提交次数
28.2K
通过率
57.6%
记忆化搜索
遍历所有的点[i][j],求出从[i][j]为起点时的递增路径长度,所有长度的最大值即为所求。正常搜索时会有很多重复操作,所以加上一个记忆化的数组f来记录从[i][j]出发的路径长度,初始化为0,在搜索[i][j]这个点时,如果f[i][j]非零,则直接返回f[i][j]的值。
class Solution {
public:int tx[4]={-1,1,0,0};int ty[4]={0,0,-1,1};int m;int n;int dfs(int x,int y,vector<vector<int>>& matrix,vector<vector<int>>& f){if(f[x][y]!=0){return f[x][y];}++f[x][y];for(int i=0;i<4;i++){int dx=x+tx[i];int dy=y+ty[i];if(dx>=0&&dx<m&&dy>=0&&dy<n&&matrix[dx][dy]>matrix[x][y]){f[x][y]=max(f[x][y],dfs(dx,dy,matrix,f)+1);}}return f[x][y];}int longestIncreasingPath(vector<vector<int>>& matrix) {m=matrix.size();n=matrix[0].size();int maxLen=0;vector<vector<int>> f(m,vector<int>(n,0));for(int i=0;i<m;i++){for(int j=0;j<n;j++){maxLen=max(maxLen,dfs(i,j,matrix,f));}}return maxLen;}
};拓补排序
在一条上升路径中,必须先经过值小的点,才能再经过值大的点。也就是说在这个图中,值更小是值更大的先决条件,并且这个图中所有的路径是不可能构成环的。对于这种存在先决条件的无环有向图,可以用拓补排序来解决。
核心代码模式(官解)
class Solution {
public:static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};int rows, columns;int longestIncreasingPath(vector< vector<int> > &matrix) {if (matrix.size() == 0 || matrix[0].size() == 0) {return 0;}rows = matrix.size();columns = matrix[0].size();auto outdegrees = vector< vector<int> > (rows, vector <int> (columns));for (int i = 0; i < rows; ++i) {for (int j = 0; j < columns; ++j) {for (int k = 0; k < 4; ++k) {int newRow = i + dirs[k][0], newColumn = j + dirs[k][1];if (newRow >= 0 && newRow < rows && newColumn >= 0 && newColumn < columns && matrix[newRow][newColumn] > matrix[i][j]) {++outdegrees[i][j];}}}}queue < pair<int, int> > q;for (int i = 0; i < rows; ++i) {for (int j = 0; j < columns; ++j) {if (outdegrees[i][j] == 0) {q.push({i, j});}}}int ans = 0;while (!q.empty()) {++ans;int size = q.size();for (int i = 0; i < size; ++i) {auto cell = q.front(); q.pop();int row = cell.first, column = cell.second;for (int k = 0; k < 4; ++k) {int newRow = row + dirs[k][0], newColumn = column + dirs[k][1];if (newRow >= 0 && newRow < rows && newColumn >= 0 && newColumn < columns && matrix[newRow][newColumn] < matrix[row][column]) {--outdegrees[newRow][newColumn];if (outdegrees[newRow][newColumn] == 0) {q.push({newRow, newColumn});}}}}}return ans;}
};自己输入数据的模式
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#include<utility>
using namespace std;
int n,m;
int height[105][105];
int outdegrees[105][105];
int tx[]={-1,1,0,0};
int ty[]={0,0,-1,1};
int main()
{cin>>n>>m;queue<pair<int,int>> p;int maxLen=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){cin>>height[i][j];outdegrees[i][j]=0;}}//初始化出度,出度为0的入队for(int i=0;i<n;i++){for(int j=0;j<m;j++){for(int k=0;k<4;k++){int dx=i+tx[k];int dy=j+ty[k];if(dx>=0&&dx<n&&dy>=0&&dy<m&&height[dx][dy]>height[i][j])++outdegrees[i][j];}if(outdegrees[i][j]==0)p.push({i,j});}}//开始拓补排序,类似于广度优先while(!p.empty()){++maxLen;int size=p.size();for(int i=0;i<size;i++){pair<int,int> cur=p.front();p.pop();int x=cur.first,y=cur.second;//更新相邻节点的出度为0的出度for(int k=0;k<4;k++){int dx=x+tx[k];int dy=y+ty[k];if(dx>=0&&dx<n&&dy>=0&&dy<n&&height[dx][dy]<height[x][y]){--outdegrees[dx][dy];if(outdegrees[dx][dy]==0){p.push({dx,dy});}}}}}cout<<maxLen;
}
相关文章:

力扣每日一题:LCR112--矩阵中的最长递增路径
题目 给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。 对于每个单元格,你可以往上,下,左,右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。 示例…...

树莓派部署yolov5实现目标检测(ubuntu22.04.3)
最近两天搞了一下树莓派部署yolov5,有点难搞(这个东西有点老,版本冲突有些包废弃了等等) 最后换到ubuntu系统弄了,下面是我的整体步骤(建议先使能一下ssh(最下面有),结合…...
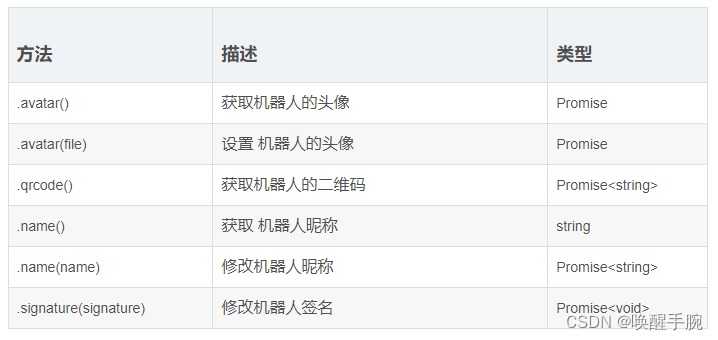
2024 年最新使用 Wechaty 开源框架搭建部署微信机器人(微信群智能客服案例)
读取联系人信息 获取当前机器人账号全部联系人信息 bot.on(ready, async () > {console.log("机器人准备完毕!!!")let contactList await bot.Contact.findAll()for (let index 0; index < contactList.length; index) {…...
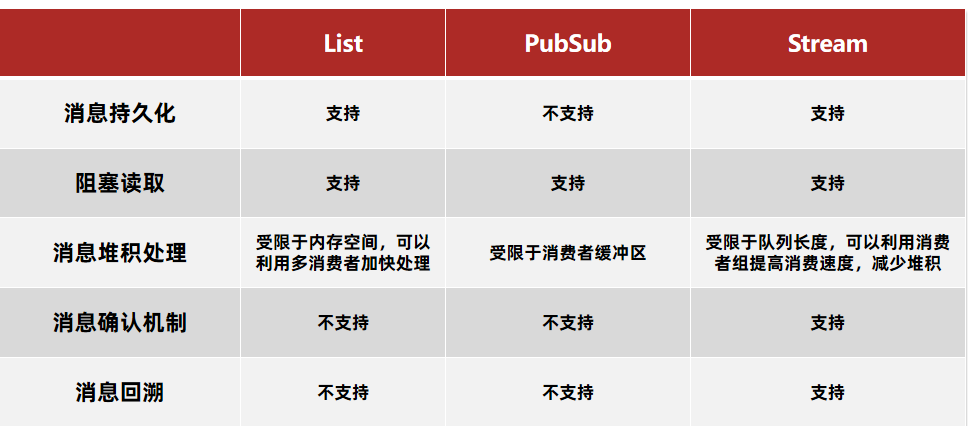
Redis从入门到精通(九)Redis实战(六)基于Redis队列实现异步秒杀下单
↑↑↑请在文章开头处下载测试项目源代码↑↑↑ 文章目录 前言4.5 分布式锁-Redisson4.5.4 Redission锁重试4.5.5 WatchDog机制4.5.5 MutiLock原理 4.6 秒杀优化4.6.1 优化方案4.6.2 完成秒杀优化 4.7 Redis消息队列4.7.1 基于List实现消息队列4.7.2 基于PubSub的消息队列4.7.…...
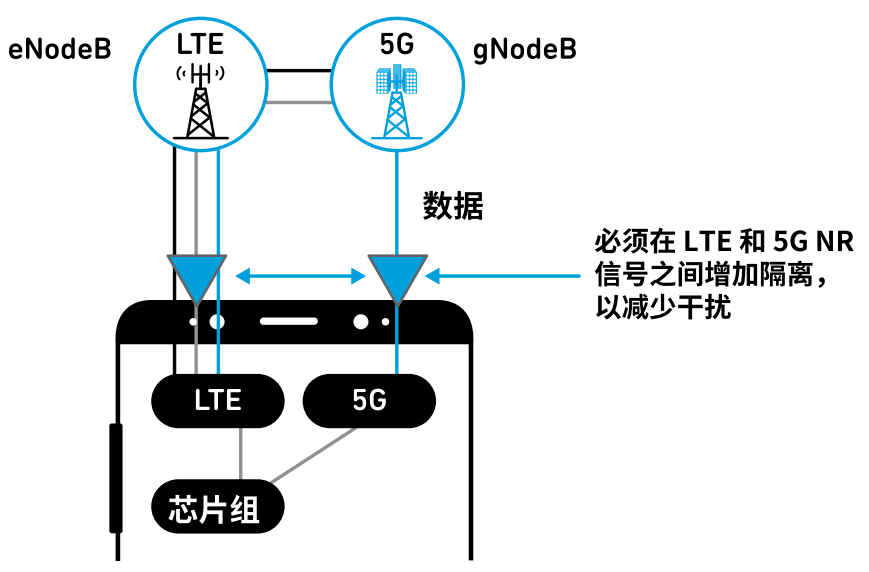
什么是多路复用器滤波器
本章将更深入地介绍多路复用器滤波器,以及它们如何用于各种应用中。您将了解到多路复用器如何帮助设计人员创造出更复杂的无线产品。 了解多路复用器 多路复用器是一组射频(RF)滤波器,它们组合在一起,但不会彼此加载,可以在输出之…...
Severt和tomcat的使用(补充)
打包程序 在pom.xml中添加上述代码之后打包时会生成war包并且包的名称是test 默认情况打的是jar包.jar里量但是tomcat要求的是war包. war包Tomcat专属的压缩包. war里面不光有.class还有一些tomcat要求的配置文件(web.xml等)还有前端的一些代码(html, css, js) 点击其右边的m…...

JavaEE初阶——多线程(一)
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 小比特 大梦想 此篇文章与大家分享多线程的第一部分:引入线程以及创建多线程的几种方式 此文章是建立在前一篇文章进程的基础上的 如果有不足的或者错误的请您指出! 1.认识线程 我们知道现代的cpu大多都是多核心…...

MongoDB主从复制模式基于银河麒麟V10系统
MongoDB主从复制模式基于银河麒麟V10系统 背景介绍 MongoDB自4.0版本开始已经不再建议使用传统的master/slave复制架构,而是全面采用了复制集(Replica Sets)作为标准的复制和高可用性解决方案。 复制集是MongoDB的一种数据复制和高可用性机制,通过异步同步数据至多个服务…...
Vue使用高德地图
1.在高德平台注册账号 2.我的 > 管理管理中添加Key 3.安装依赖 npm i amap/amap-jsapi-loader --save 或 yarn add amap/amap-jsapi-loader --save 4.导入 AMapLoade import AMapLoader from amap/amap-jsapi-loader; 5.直接上代码,做好了注释(初始化…...
)
2024-04-07(复盘前端)
---HTML 1.HTMl骨架 html:整个网页 head:网页头部,用来存放给浏览器看的信息,如css body:网页主体,用来存放给用户看的信息,例如图片和文字 2.标题标签中h1标签只能使用一次,其…...
SpringCloud学习(10)-SpringCloudAlibaba-Nacos服务注册、配置中心
Spring Cloud Alibaba 参考文档 Spring Cloud Alibaba 参考文档 nacos下载Nacos 快速开始 直接进入bin包 运行cmd命令:startup.cmd -m standalone 运行成功后通过http://localhost:8848/nacos进入nacos可视化页面,账号密码默认都是nacos Nacos服务注…...

OKCC外呼中心配置的电话系统规则
OKCC外呼中心配置电话系统规则可能涉及多个方面,包括呼叫路由、自动化流程、电话接听策略等。以下是一般步骤及注意事项: 呼叫路由配置: 确定呼叫中心的呼叫路由策略,包括如何分配呼叫给不同的坐席或部门。设置呼叫路由规则&#…...
:2024.03.31-2024.04.05)
AI推介-大语言模型LLMs论文速览(arXiv方向):2024.03.31-2024.04.05
文章目录~ 1.AutoWebGLM: Bootstrap And Reinforce A Large Language Model-based Web Navigating Agent2.Training LLMs over Neurally Compressed Text3.Unveiling LLMs: The Evolution of Latent Representations in a Temporal Knowledge Graph4.Visualization-of-Thought …...
使用详解)
性能测试工具 ab(Apache Bench)使用详解
Apache Bench (ab) 是一个由 Apache 提供的非常流行的、简单的性能测试工具,用于对 HTTP 服务器进行压力测试。下面是 ab 工具的一些基本使用方法。 安装 在大多数 Unix 系统中,ab 通常作为 Apache HTTP 服务器的一部分预装在系统中。你可以通过在终端…...

智能网联汽车自动驾驶数据记录系统DSSAD数据元素
目录 第一章 数据元素分级 第二章 数据元素分类 第三章 数据元素基本信息表 表1 车辆及自动驾驶数据记录系统基本信息 表2 车辆状态及动态信息 表3 自动驾驶系统运行信息 表4 行车环境信息 表5 驾驶员操作及状态信息 第一章 数据元素分级 自动驾驶数据记录系统记录的数…...

Ubuntu 20.04.06 PCL C++学习记录(十八)
[TOC]PCL中点云分割模块的学习 学习背景 参考书籍:《点云库PCL从入门到精通》以及官方代码PCL官方代码链接,,PCL版本为1.10.0,CMake版本为3.16 学习内容 PCL中实现欧式聚类提取。在点云处理中,聚类是一种常见的任务,它将点云数据划分为多…...

细雨踏春日,新会公安护平安
春雨起,清明至。又是一年春草绿,又是一年清明时。细雨踏春日,思怀故人时,是哀思,亦是相聚。新会公安一抹抹葵乡春日“警”色坚守岗位,确保清明祭扫平稳有序,为人民群众的平安保驾护航。 为确保2…...

3d怎么在一块模型上开个孔---模大狮模型网
在进行3D建模时,有时候需要在模型上创建孔,以实现特定的设计需求或功能。无论是为了添加细节,还是为了实现功能性的要求,创建孔都是常见的操作之一。本文将介绍在3D模型上创建孔的几种常用方法,帮助您轻松实现这一目标…...
Python景区票务人脸识别系统(V2.0),附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

全球化业务的网络安全挑战
随着企业业务的全球化,跨国数据传输和用户跨地域访问成为常态。这不仅带来了巨大的商业机会,也带来了以下网络安全挑战: 数据泄露风险:跨国数据传输增加了数据被截获和泄露的风险。访问限制:某些地区可能对互联网内容…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
