Python | Leetcode Python题解之第14题最长公共前缀
题目:
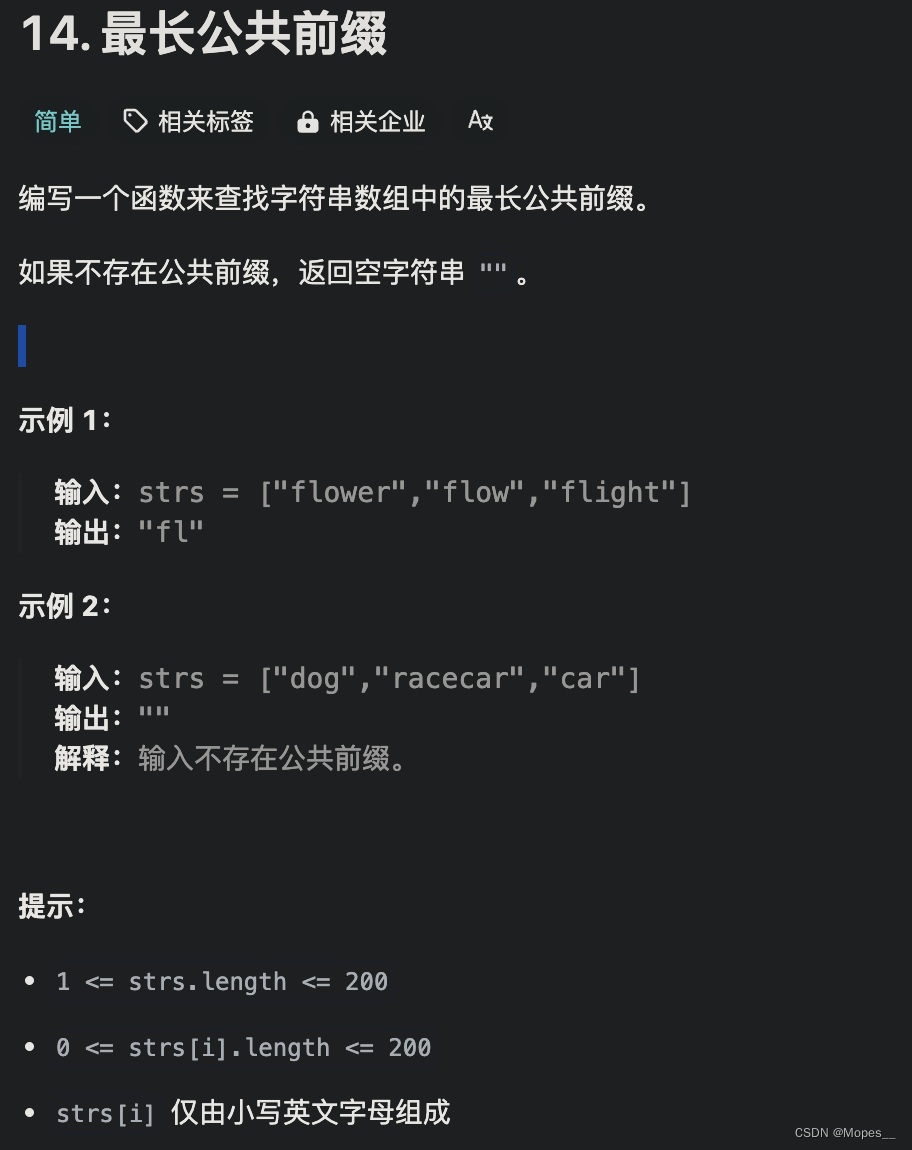
题解:
class Solution:def longestCommonPrefix(self, strs: List[str]) -> str:def isCommonPrefix(length):str0, count = strs[0][:length], len(strs)return all(strs[i][:length] == str0 for i in range(1, count))if not strs:return ""minLength = min(len(s) for s in strs)low, high = 0, minLengthwhile low < high:mid = (high - low + 1) // 2 + lowif isCommonPrefix(mid):low = midelse:high = mid - 1return strs[0][:low]相关文章:

Python | Leetcode Python题解之第14题最长公共前缀
题目: 题解: class Solution:def longestCommonPrefix(self, strs: List[str]) -> str:def isCommonPrefix(length):str0, count strs[0][:length], len(strs)return all(strs[i][:length] str0 for i in range(1, count))if not strs:return &quo…...
烧坏两块单片机,不知道原因?
没有看你的原理图,以下是造成烧毁芯片的几个环节: 1. 最大的可能性是你的单片机电机控制输出与电机驱动电路没有隔离。 我的经验,使用STM32控制电机,无论是直流电机脉宽调制,还是步进电机控制,控制电路与…...
)
SV学习笔记(八)
文章目录 SV入门练习基本数据类型字符串类型数组类型接口的定义与例化类的封装类的继承package的使用随机约束线程的同步线程的控制虚方法方法(任务与函数)SV用于设计 参考资料 SV入门练习 基本数据类型 有符号无符号、四状态双状态、枚举类型、结构体…...

Java反射常用方法
反射 作用: 对于任意一个对象,把对象所有的字段名和值,保存到文件中去利用反射动态的创造对象和运行方法 1. 获取字节码文件对象 方法描述Class.forName(String)通过类的全限定名字符串获取字节码文件对象。类字面量直接使用类的字面量获…...
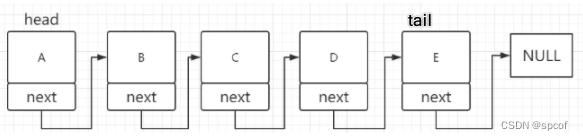
go语言实现无头单向链表
什么是无头单向链表 无头单向链表是一种线性数据结构,它的每个元素都是一个节点,每个节点都有一个指向下一个节点的指针。"无头"意味着这个链表没有一个特殊的头节点,链表的第一个节点就是链表的头。 优点: 动态大小&…...

SpringBoot快速入门笔记(5)
文章目录 一、elemetnUI1、main.js2、App.vue3、fontAwesome 一、elemetnUI 开源前端框架,安装 npm i element-ui -S 建议查看官方文档 Element组件,这里是Vue2搭配elementUI,如果是vue3就搭配elementPlus,这里初学就以Vue2为例子…...

solidity(3)
地址类型 pragma solidity ^0.8.0;contract AddressExample {// 地址address public _address 0x7A58c0Be72BE218B41C608b7Fe7C5bB630736C71;address payable public _address1 payable(_address); // payable address,可以转账、查余额// 地址类型的成员uint256…...

笔记 | 编译原理L1
重点关注过程式程序设计语言编译程序的构造原理和技术 1 程序设计语言 1.1 依据不同范型 过程式(Procedural programming languages–imperative)函数式(Functional programming languages–declarative)逻辑式(Logical programming languages–declarative)对象式(Object-or…...
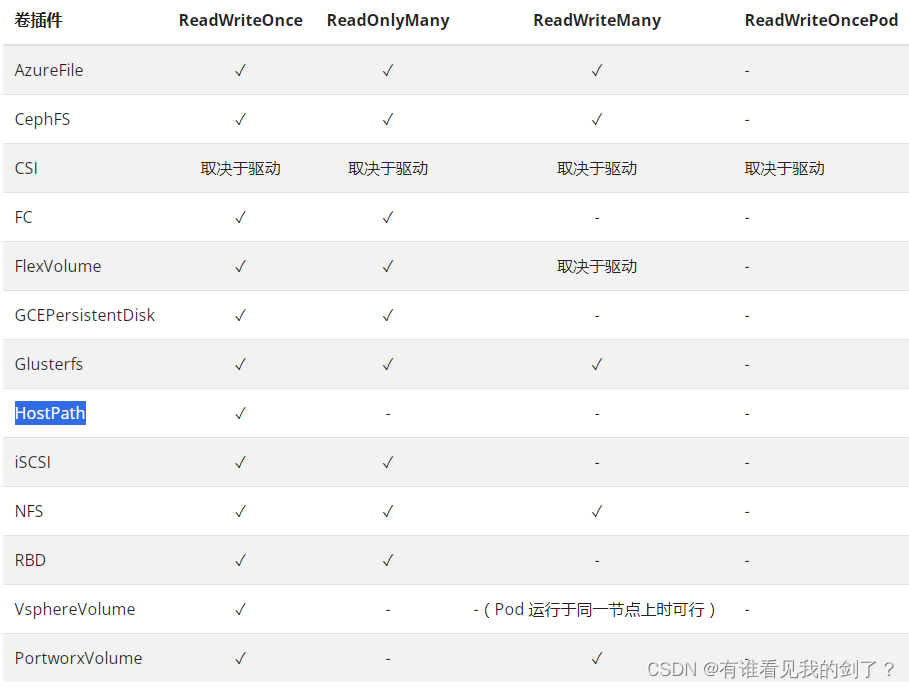
k8s存储卷 PV与PVC 理论学习
介绍 存储的管理是一个与计算实例的管理完全不同的问题。PersistentVolume 子系统为用户和管理员提供了一组 API,将存储如何制备的细节从其如何被使用中抽象出来。为了实现这点,我们引入了两个新的 API 资源:PersistentVolume 和 Persistent…...

【WPF应用32】WPF中的DataGrid控件详解与示例
在WPF(Windows Presentation Foundation)开发中,DataGrid控件是一个强大的数据绑定工具,它以表格的形式展示数据,并支持复杂的编辑、排序、过滤和分组等操作。在本文中,我们将详细介绍DataGrid控件的功能、…...
numpy,matplotilib学习(菜鸟教程)
所有内容均来自于: NumPy 教程 | 菜鸟教程 Matplotlib 教程 | 菜鸟教程 numpy模块 numpy.nditer NumPy 迭代器对象 numpy.nditer 提供了一种灵活访问一个或者多个数组元素的方式。 for x in np.nditer(a, orderF):Fortran order,即是列序优先&#x…...
之日期对象节点操作js插件重绘和回流)
Web API(四)之日期对象节点操作js插件重绘和回流
Web API(四)之日期对象&节点操作&js插件&重绘和回流 日期对象实例化方法时间戳DOM 节点插入节点删除节点查找节点父子关系兄弟关系M端事件js插件重绘和回流进一步学习 DOM 相关知识,实现可交互的网页特效 能够插入、删除和替换元素节点能够依据元素节点关系查找…...

27.WEB渗透测试-数据传输与加解密(1)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:26.WEB渗透测试-BurpSuite(五) BP抓包网站网址:http:…...

山寨windows
我的目标是能够运行windows 下的大部分PE格式的程序,这一点通过实验已经证明完全是可行的。 PE格式主要有exe dll sys等文件,这三个文件可以用相同的函数解析, 主要有以下段组成, 1、文件头,包含DOS文件头、PE文件头…...

unity工程输出的log在哪里?
在编辑器里进行活动输出的log位置: C:\Users\username\AppData\Local\Unity\Editor\Editor.log ------------------------------------ 已经打包完成,形成的exe运行后的log位置: C:\Users\xxx用户\AppData\LocalLow\xx公司\xx项目...

【力扣】7. 整数反转
7. 整数反转 题目描述 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 …...

Android Apk签名算法使用SHA256
Android apk签名算法使用SHA256 本文不介绍复杂的签名过程,说一下Android签名算法使用SHA256。 但是SHA1不是相对安全签名算法,SHA256更加安全一些。 一般大公司才会有这种细致的安全要求。 如何查看apk签名是否是SHA1还是SHA256 1、拿到apk文件&…...

2024.3.13力扣每日一题——最大二进制奇数
2024.3.13 题目来源我的题解方法一 贪心 题目来源 力扣每日一题;题序:2864 我的题解 方法一 贪心 统计1的个数,满足要求的字符串的末尾一位一定是1,所以需要将一位1放到末尾,然后将剩余的1从最高位开始放࿰…...

2024.4.1力扣每日一题——故障键盘
2024.4.1 题目来源我的题解方法一 直接利用StringBuilder的反转函数方法二 字符数组 题目来源 力扣每日一题;题序:2810 我的题解 方法一 直接利用StringBuilder的反转函数 使用StringBuilder构造结果,并利用其反转函数进行翻转 时间复杂度…...

第十四届蓝桥杯C/C++大学B组题解(一)
1、日期统计 #include <bits/stdc.h> using namespace std; int main() {int array[100] {5, 6, 8, 6, 9, 1, 6, 1, 2, 4, 9, 1, 9, 8, 2, 3, 6, 4, 7, 7,5, 9, 5, 0, 3, 8, 7, 5, 8, 1, 5, 8, 6, 1, 8, 3, 0, 3, 7, 9,2, 7, 0, 5, 8, 8, 5, 7, 0, 9, 9, 1, 9, 4, 4, 6,…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...
