买卖股票的最佳时机III
题目链接
买卖股票的最佳时机III
题目描述
注意点
- 1 <= prices.length <= 100000
- 0 <= prices[i] <= 100000
- 不能同时参与多笔交易(必须在再次购买前出售掉之前的股票)
- 最多可以完成 两笔 交易
解答思路
- 本题最多可以完成两笔交易,所以在任意一天,都会有五种状态,分别是无操作、第一次买入、第一次卖出、第二次买入、第二次卖出。需要注意的是,当天同时买入卖出是无意义的,利润不会改变,仅仅是增加了交易次数,不在考虑范围之内。同时无操作的利润始终为0,可以忽略不记,所以将每一天都分割成其余四种状态
- 关键是怎么通过第i - 1天推出第i天四种状态的最大利润,可以分为以下几种
- 当处于第一次买入的状态,其可能是当天购入也可能是之前就已经购入,取决于哪天购买的成本更低,所以dp[i][0] = Math.max(dp[i - 1][0], -prices[i]),注意当天购入的话需要花费prices[i]的成本,所以为负数
- 当处于第一次卖出的状态,其可能是当天买出也可能是之前就已经卖出,取决于哪天卖出的利润更高,所以dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]),dp[i - 1][0]是第一次购买最低的成本,其可以保证当天卖出在前i天当中所得到的利润是最大的
- 当处于第二次买入的状态,其与第一次买入的状态类似,区别是第一次已经交易成功了,所以如果当天买入的话dp[i][2]的值还要加上第一次交易所得到的最大利润,也就是dp[i - 1][1],所以dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] - prices[i])
- 当处于第二次卖入的状态,其与第二次卖出的状态类似,dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] + prices[i])
- 需要注意的是,dp[0][2]与dp[0][0]一样,初始需要给默认值-prices[0],在第一次交易未完成时,dp[i][2]实际上始终与dp[i][0]相同,dp[i][3]与dp[i][1]也是如此,实际上此时第二次交易也是第一次交易(因为dp[i - 1][1]始终都为0,此时dp[i][2] = Math.max(dp[i - 1][2], - prices[i]))。当第一次交易完成时,dp[i][2]就需要在第一次交易获得利润的基础上进行考虑,其购买的成本会变为dp[i - 1][1] - prices[i]
代码
class Solution {public int maxProfit(int[] prices) {int n = prices.length;// 二维数组,dp[i][j]表示第i天时处于第j中状态的最大利润/*** j有以下四种状态* 0:第一次买入股票* 1:第一次卖出股票(也就是完成第一次交易)* 2:第二次买入股票* 3:第二次卖出股票(也就是完成第二次交易)* 不做任何操作也是一种状态,但是对结果无影响不考虑*/int[][] dp = new int[n][4];dp[0][0] = -prices[0];dp[0][2] = -prices[0];for (int i = 1; i < n; i++) {// 第i天购买或者之前就已购买,取购买花费更低的成本dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);// 第i天卖出或者之前就已卖出,取卖出得到更高的利润dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);// 第i天购买或者之前就已购买,取购买花费更低的成本,第二次交易还要加上第一次交易所得的利润dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] - prices[i]);// 第i天卖出或者之前就已卖出,取卖出得到更高的利润dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] + prices[i]);}return Math.max(dp[n - 1][1], dp[n - 1][3]);}
}
关键点
- 动态规划的思想
- 每天买卖股票的四种状态
- 怎么根据dp[i - 1][j]推出dp[i][j]
相关文章:
买卖股票的最佳时机III
题目链接 买卖股票的最佳时机III 题目描述 注意点 1 < prices.length < 1000000 < prices[i] < 100000不能同时参与多笔交易(必须在再次购买前出售掉之前的股票)最多可以完成 两笔 交易 解答思路 本题最多可以完成两笔交易,…...

fastlio2 保存每帧的点云和每帧的里程计为单独的文件做后端回环优化和手动回环优化
为了 提供数据做后端回环优化和手动回环优化,需要保存每帧的点云和每帧的里程计为单独的文件,并且需要保存的名字为ros时间戳。 效果很好,比我自己写的手动回环模块好用 // This is an advanced implementation of the algorithm described in the // following paper: /…...

【线段树】【前缀和】:1687从仓库到码头运输箱子
本题简单解法 C前缀和算法的应用:1687从仓库到码头运输箱子 本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 线段树 LeetCode1687从仓库到码头运输箱子 你有一辆货运卡车,你需要用这一辆车…...

[AIGC] 实现博客平台的推荐排行榜
推荐排行榜是许多网站和平台的重要特性,它可以把最受欢迎或最具价值的内容展示给用户。本文将详细介绍如何为博客网站实现一个推荐排行榜。 文章目录 一、选择推荐指标二、收集数据三、设计排行榜算法四、显示推荐排行榜五、demo总结 一、选择推荐指标 实现推荐排行…...

C++利用键值对计算某一个数对应的最值及其索引位置
目录 一、算法概述二、代码实现1、计算最值2、计算最值及其索引 三、结果展示 本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法概述 类似下图所示,计算第一列中1或2对应的最…...
conda修改默认安装python版本为指定版本
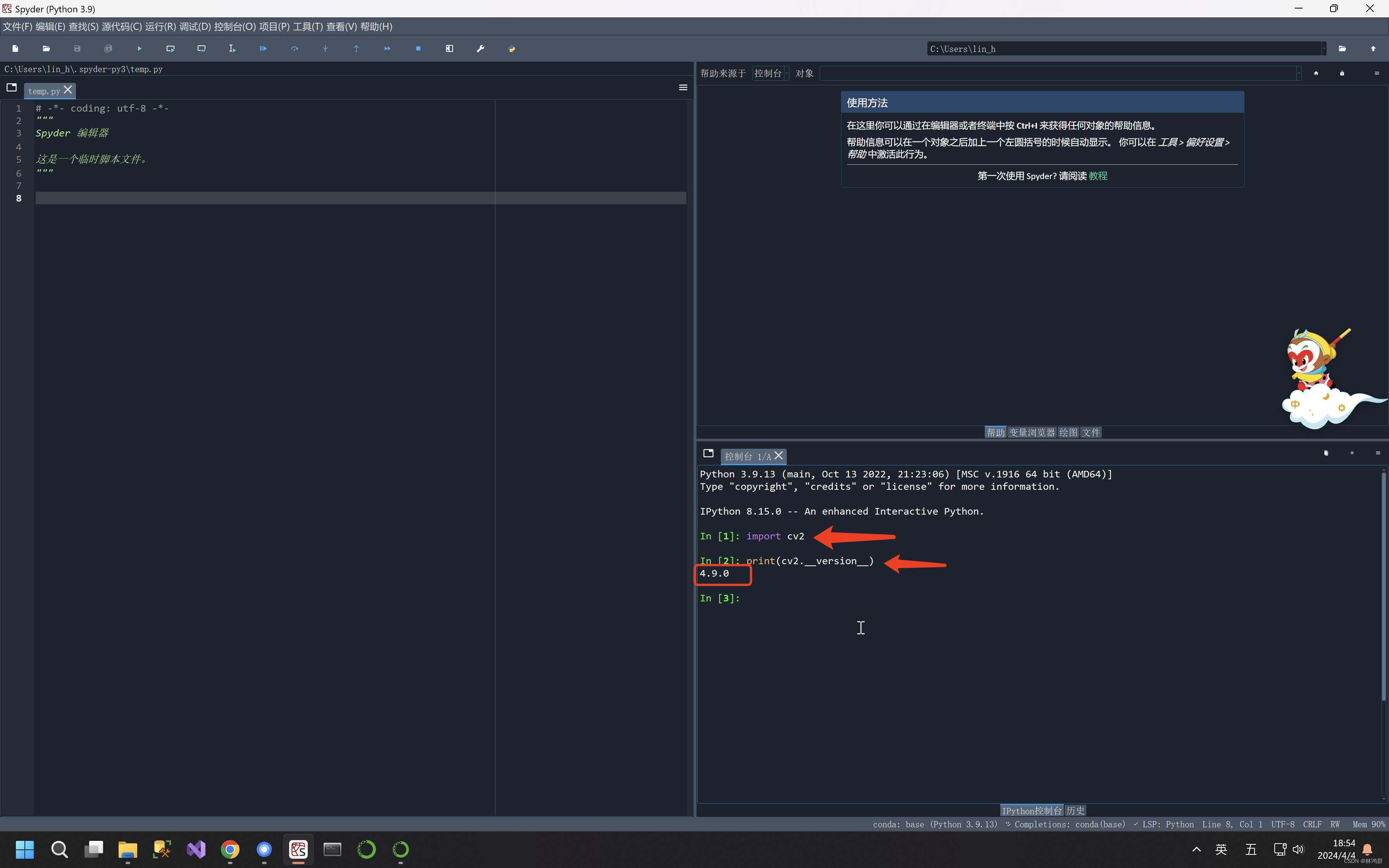
1.查看conda中当前的python版本号: 打开Anaconda Powershell Prompt 输入python -V 回车会输出版本号 2.查看conda所支持的python版本,并选择指定版本安装 选择一个3.9.13版本的进行安装 安装命令: conda install python3.9.13 如果一直卡在这个画面,请使用管理员权限运行…...
 -- 游戏(TODO))
显示学习番外篇(基于树莓派Pico) -- 游戏(TODO)
来自:11.4. 飞行小鸟 — mPython掌控 2.2.0 documentation (TODO)...

顺序表实战——基于顺序表的通讯录
前言:本篇文章主要是利用顺序表作为底层, 实现一个通讯录。偏向于应用, 对于已经学习过c的友友们可能没有难度了已经。没有学习过c的友友, 如果顺序表不会写, 或者说没有自己实现过, 请移步学习顺序表相关内…...

创建型模式--1.单例模式【巴基速递】
1. 巴基的订单 在海贼世界中,巴基速递是巴基依靠手下强大的越狱犯兵力,组建的集团海贼派遣公司,它的主要业务是向世界有需要的地方输送雇佣兵(其实是不干好事儿)。 自从从特拉法尔加罗和路飞同盟击败了堂吉诃德家族 &…...
用 Wireshark 解码 H.264
H264,你不知道的小技巧-腾讯云开发者社区-腾讯云 这篇文章写的非常好 这里仅做几点补充 init.lua内容: -- Set enable_lua to false to disable Lua support. enable_lua trueif not enable_lua thenreturn end-- If false and Wireshark was start…...

鸿蒙TypeScript学习第10天:【String(字符串)】
1、TypeScript String(字符串) String 对象用于处理文本(字符串)。 语法 var txt new String("string"); 或者更简单方式: var txt "string"; 2、String 对象属性 下表列出了 String 对象支…...

【201】Java8读取JSON树形结构并插入到MySQL数据库表中
我写了一个 maven 项目的 Demo,用来演示 JAVA8 如何读取 JSON 文件树形结构,并将这种树形结构保存到 MySQL 中。 json文件 city.json {"name": "山东省","sub": [{"name": "青岛市","sub"…...

AI“复活”:慰藉心灵还是触碰禁忌?一文看懂技术与伦理的较量|TodayAI
随着人工智能(AI)技术的迅猛发展,其应用领域也越来越广泛,不仅仅局限于数据分析、机器人自动化等传统领域,更是延伸到了一些人们曾经认为只存在于科幻小说中的领域。近年来,使用AI技术“复活”逝者的概念&a…...
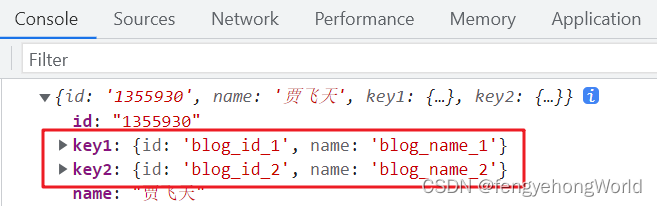
Jackson @JsonUnwrapped注解扁平化 序列化反序列化数据
参考资料 Jackson 2.x 系列【7】注解大全篇三JsonUnwrapped 以扁平的数据结构序列化/反序列化属性Jackson扁平化处理对象 目录 一. 前期准备1.1 前端1.2 实体类1.3 Controller层 二. 扁平化序列反序列化数据2.1 序列化数据2.2 反序列化数据 三. 前缀后缀处理属性同名四. Map数…...

日期时间相关的类
分界线jdk8 jdk8之前和之后分别提供了一些日期和时间的类,推荐使用jdk8之后的日期和时间类 Date类型 这是一个jdk8之前的类型,其中有很多方法已经过时了,选取了一些没有过时的API //jdk1.8之前的日期 Date Date date new Date(); // 从1970年…...

微信小程序脚本的执行顺序
在小程序中的脚本执行顺序和浏览器中有所不同。 小程序的执行的入口文件是 app.js 。 并且会根据其中 require 的模块顺序决定文件的运行顺序,代码是一个 app.js 示例。 app.js /* a.js console.log(a.js) */ var a require(./a.js) console.log(app.js)/* b.js co…...

zabbix监控警告
监控概述 对服务的管理,不能仅限于可用性。 还需要服务可以安全、稳定、高效地运行。 监控的目的:早发现、早治疗。 被监控的资源类型: 公开数据:对外开放的,不需要认证即可获取的数据 私有数据:对外不…...
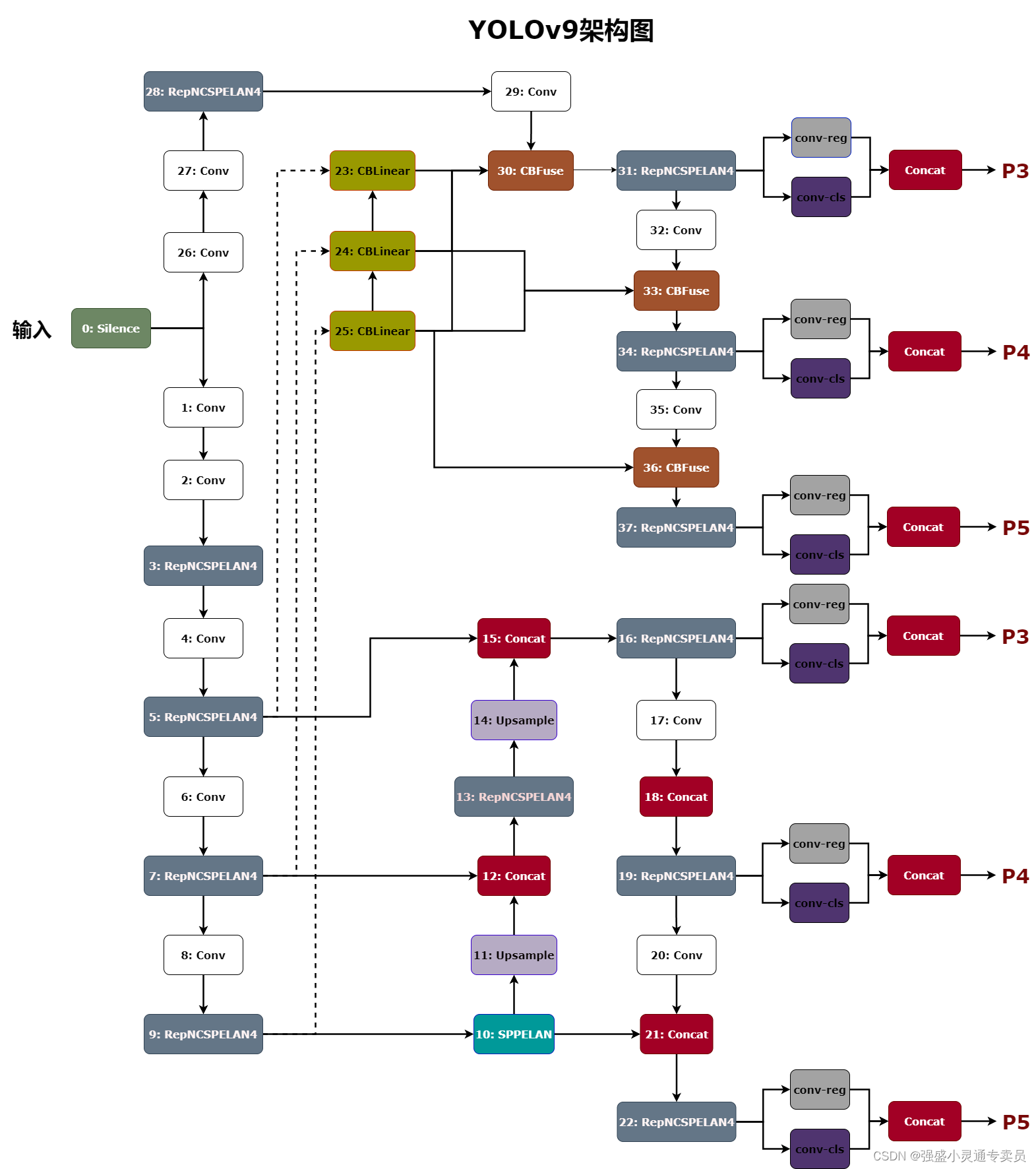
YOLOv9架构图分享
YOLOv9是YOLO (You Only Look Once)系列实时目标检测系统的最新迭代。它建立在以前的版本之上,结合了深度学习技术和架构设计的进步,以在目标检测任务中实现卓越的性能。通过将可编程梯度信息(PGI)概念与广义ELAN (GELAN)架构相结合,YOLOv9在…...

全自动封箱机的工作原理:科技与效率的完美结合
随着科技的不断发展,越来越多的自动化设备走进了我们的日常生活和工业生产中。其中,全自动封箱机作为物流包装领域的重要一环,凭借其高效、精准的工作性能,正逐渐成为提升生产效率、降低劳动成本的得力助手。星派就来与大家深入探…...
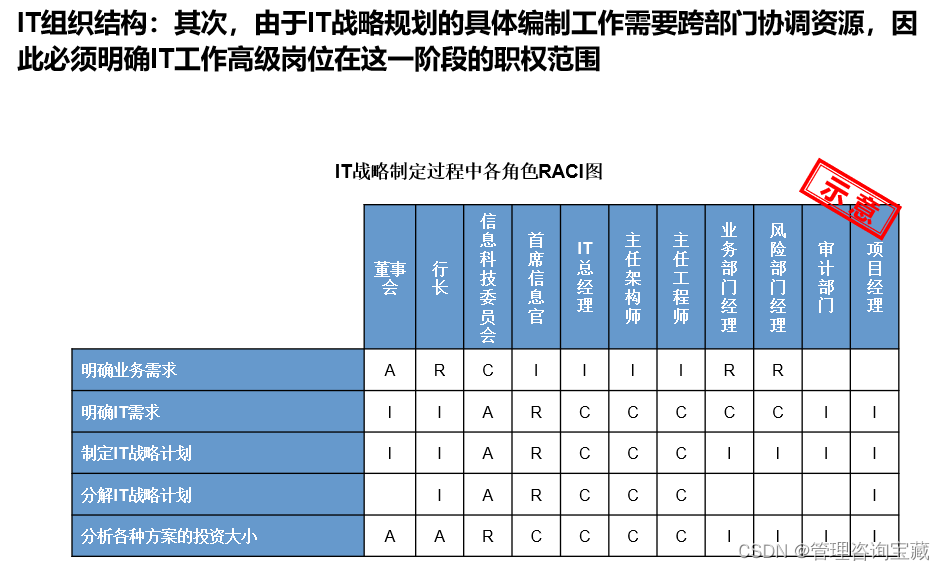
【管理咨询宝藏48】AA银行信息科技提升分析报告
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏48】AA银行信息科技提升分析报告 【格式】PPT版本,可编辑 【关键词】战略规划、商业分析、管理咨询 【强烈推荐】这是一套市面上非常…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...

