浏览器禁用cookie后session还能用吗?
1.背景
最近有朋友问我其面试时遇到的一个不常见的问题:浏览器禁用cookie后session还能用吗?,怎么解答。
2.cookie与session联系入手
2.1 理论基础
一般默认情况下,在会话中,服务器存储 session 的 sessionid ,而sessionid 是通过 cookie 存在浏览器里的。如果浏览器禁用了 cookie,那么浏览器请求服务器时将无法携带 sessionid,进而服务器无法识别请求中的用户身份,所以,session失效,不能正常使用。
2.2 具体解释
服务器端调用了requet.getSession()的时候, 产生session对象。创建session的同时 生成sessionId(代表唯一sesssion的字符串), 服务器自动通过Cookie的方式写给浏览器。下次浏览器携带cookie(SessionId)找到对应的session使用。如果用户禁用cookie,则cookie(SessionId)无法存储,浏览器每次访问都不携带任何cookie,包括cookie(SessionId)。
相关文章:

浏览器禁用cookie后session还能用吗?
1.背景 最近有朋友问我其面试时遇到的一个不常见的问题:浏览器禁用cookie后session还能用吗?,怎么解答。 2.cookie与session联系入手 2.1 理论基础 一般默认情况下,在会话中,服务器存储 session 的 sessionid &…...
C语言——顺序表
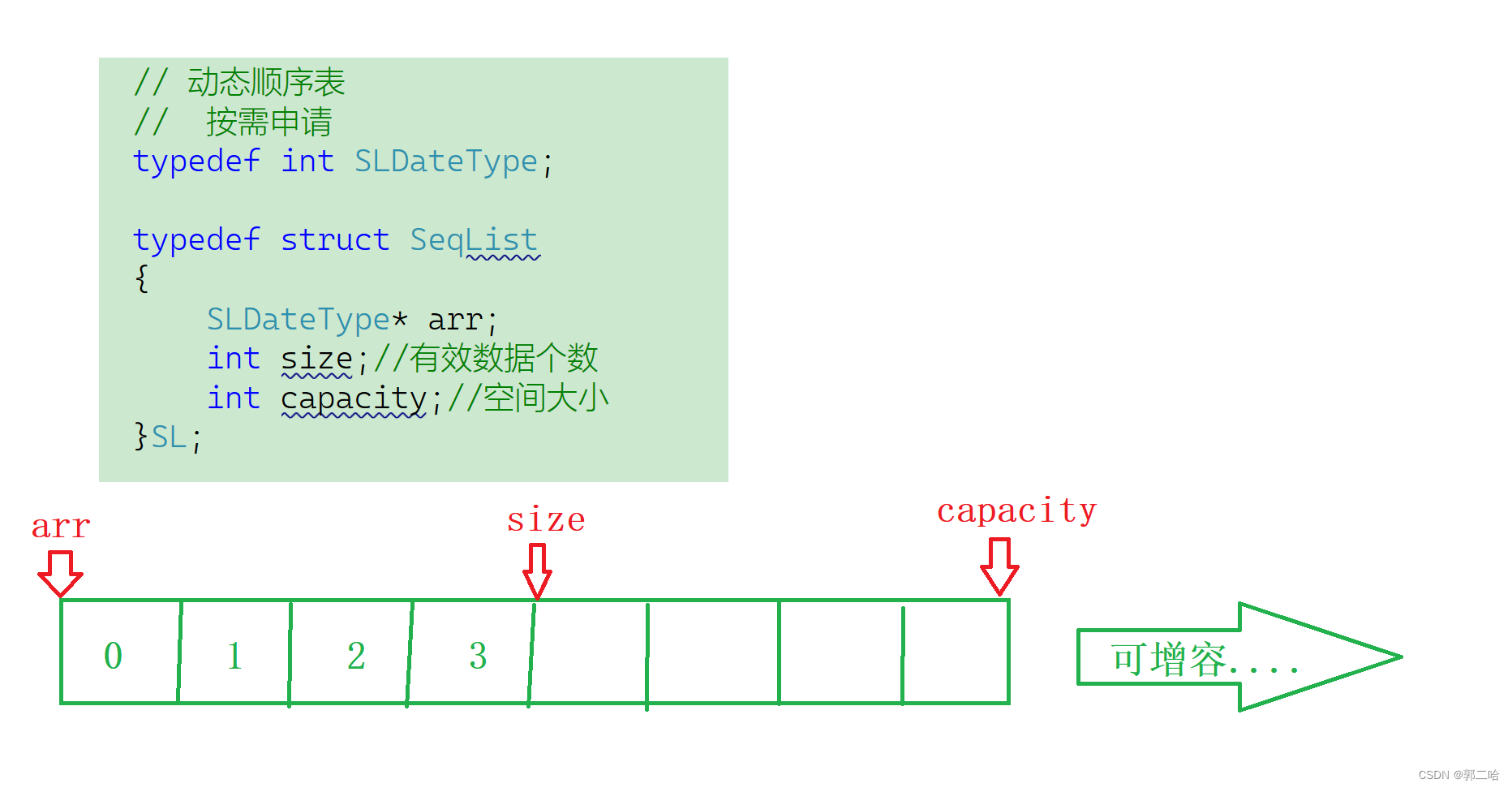
文章目录 一、线性表二、顺序表顺序表和数组的区别顺序表的分类1.静态顺序表2.动态顺序表 三、动态顺序表的实现1.动态顺序表头文件2.动态顺序表源文件3.测试源文件 一、线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。线性表是⼀种…...

CentOS7安装Docker及禅道
https://blog.csdn.net/weixin_46453070/article/details/136183615?ops_request_misc%257B%2522request%255Fid%2522%253A%2522171246925816800222886233%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id171246925816800222886233&biz_i…...
如何在社交媒体中使用增强现实来提高客户参与度?
目录 1. 增强现实在社交媒体中的应用是如何发展的 2. 社交媒体营销和广告中的增强现实 3. 社交媒体上的增强现实滤镜和镜头 4. 社交媒体平台上的增强现实购物 5. 利用社交媒体的增强现实事件和品牌激活 6. 增强现实在社交媒体中的未来是什么 7. 社交媒体中的增强现实常见…...

Autodesk AutoCAD 2025 (macOS, Windows) - 自动计算机辅助设计软件
Autodesk AutoCAD 2025 (macOS, Windows) - 自动计算机辅助设计软件 AutoCAD 2024 开始原生支持 Apple Silicon,性能提升至 2 倍 请访问原文链接:https://sysin.org/blog/autodesk-autocad/,查看最新版。原创作品,转载请保留出处…...
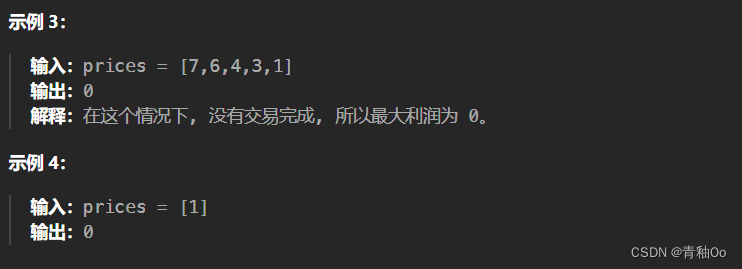
买卖股票的最佳时机III
题目链接 买卖股票的最佳时机III 题目描述 注意点 1 < prices.length < 1000000 < prices[i] < 100000不能同时参与多笔交易(必须在再次购买前出售掉之前的股票)最多可以完成 两笔 交易 解答思路 本题最多可以完成两笔交易,…...

fastlio2 保存每帧的点云和每帧的里程计为单独的文件做后端回环优化和手动回环优化
为了 提供数据做后端回环优化和手动回环优化,需要保存每帧的点云和每帧的里程计为单独的文件,并且需要保存的名字为ros时间戳。 效果很好,比我自己写的手动回环模块好用 // This is an advanced implementation of the algorithm described in the // following paper: /…...

【线段树】【前缀和】:1687从仓库到码头运输箱子
本题简单解法 C前缀和算法的应用:1687从仓库到码头运输箱子 本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 线段树 LeetCode1687从仓库到码头运输箱子 你有一辆货运卡车,你需要用这一辆车…...

[AIGC] 实现博客平台的推荐排行榜
推荐排行榜是许多网站和平台的重要特性,它可以把最受欢迎或最具价值的内容展示给用户。本文将详细介绍如何为博客网站实现一个推荐排行榜。 文章目录 一、选择推荐指标二、收集数据三、设计排行榜算法四、显示推荐排行榜五、demo总结 一、选择推荐指标 实现推荐排行…...

C++利用键值对计算某一个数对应的最值及其索引位置
目录 一、算法概述二、代码实现1、计算最值2、计算最值及其索引 三、结果展示 本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法概述 类似下图所示,计算第一列中1或2对应的最…...
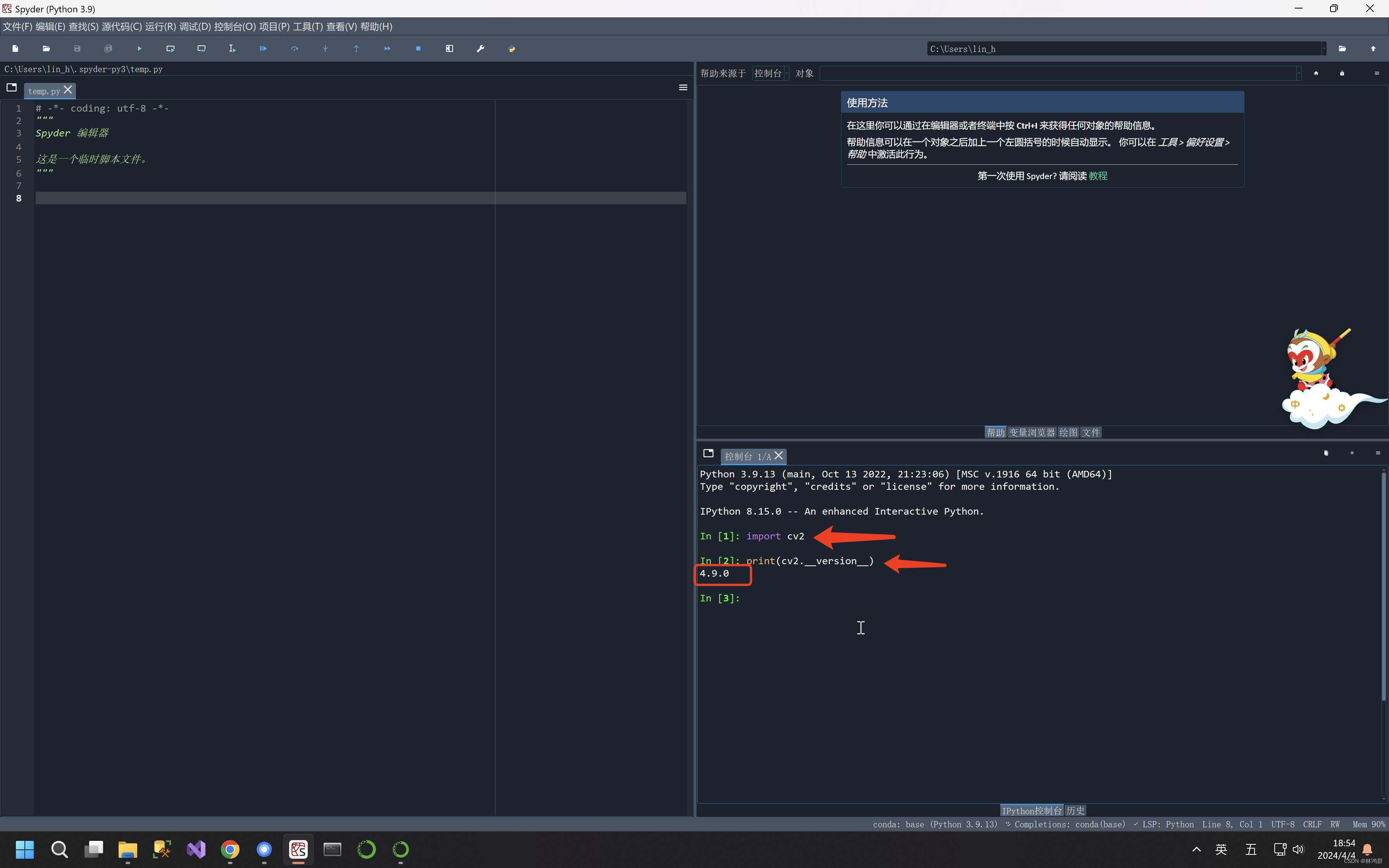
conda修改默认安装python版本为指定版本
1.查看conda中当前的python版本号: 打开Anaconda Powershell Prompt 输入python -V 回车会输出版本号 2.查看conda所支持的python版本,并选择指定版本安装 选择一个3.9.13版本的进行安装 安装命令: conda install python3.9.13 如果一直卡在这个画面,请使用管理员权限运行…...
 -- 游戏(TODO))
显示学习番外篇(基于树莓派Pico) -- 游戏(TODO)
来自:11.4. 飞行小鸟 — mPython掌控 2.2.0 documentation (TODO)...

顺序表实战——基于顺序表的通讯录
前言:本篇文章主要是利用顺序表作为底层, 实现一个通讯录。偏向于应用, 对于已经学习过c的友友们可能没有难度了已经。没有学习过c的友友, 如果顺序表不会写, 或者说没有自己实现过, 请移步学习顺序表相关内…...

创建型模式--1.单例模式【巴基速递】
1. 巴基的订单 在海贼世界中,巴基速递是巴基依靠手下强大的越狱犯兵力,组建的集团海贼派遣公司,它的主要业务是向世界有需要的地方输送雇佣兵(其实是不干好事儿)。 自从从特拉法尔加罗和路飞同盟击败了堂吉诃德家族 &…...
用 Wireshark 解码 H.264
H264,你不知道的小技巧-腾讯云开发者社区-腾讯云 这篇文章写的非常好 这里仅做几点补充 init.lua内容: -- Set enable_lua to false to disable Lua support. enable_lua trueif not enable_lua thenreturn end-- If false and Wireshark was start…...

鸿蒙TypeScript学习第10天:【String(字符串)】
1、TypeScript String(字符串) String 对象用于处理文本(字符串)。 语法 var txt new String("string"); 或者更简单方式: var txt "string"; 2、String 对象属性 下表列出了 String 对象支…...

【201】Java8读取JSON树形结构并插入到MySQL数据库表中
我写了一个 maven 项目的 Demo,用来演示 JAVA8 如何读取 JSON 文件树形结构,并将这种树形结构保存到 MySQL 中。 json文件 city.json {"name": "山东省","sub": [{"name": "青岛市","sub"…...

AI“复活”:慰藉心灵还是触碰禁忌?一文看懂技术与伦理的较量|TodayAI
随着人工智能(AI)技术的迅猛发展,其应用领域也越来越广泛,不仅仅局限于数据分析、机器人自动化等传统领域,更是延伸到了一些人们曾经认为只存在于科幻小说中的领域。近年来,使用AI技术“复活”逝者的概念&a…...
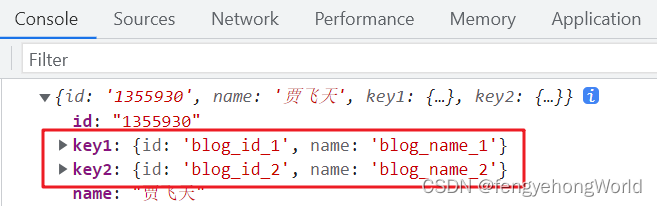
Jackson @JsonUnwrapped注解扁平化 序列化反序列化数据
参考资料 Jackson 2.x 系列【7】注解大全篇三JsonUnwrapped 以扁平的数据结构序列化/反序列化属性Jackson扁平化处理对象 目录 一. 前期准备1.1 前端1.2 实体类1.3 Controller层 二. 扁平化序列反序列化数据2.1 序列化数据2.2 反序列化数据 三. 前缀后缀处理属性同名四. Map数…...

日期时间相关的类
分界线jdk8 jdk8之前和之后分别提供了一些日期和时间的类,推荐使用jdk8之后的日期和时间类 Date类型 这是一个jdk8之前的类型,其中有很多方法已经过时了,选取了一些没有过时的API //jdk1.8之前的日期 Date Date date new Date(); // 从1970年…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
