0203逆矩阵-矩阵及其运算-线性代数
文章目录
- 一、逆矩阵的定义、性质和求法
- 二、逆矩阵的初步应用
- 结语
一、逆矩阵的定义、性质和求法
定义7 对于 n n n阶矩阵A,如果有一个 n n n阶矩阵B,使
A B = B A = E AB=BA=E AB=BA=E
则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆阵。
定理1 若矩阵A可逆,则 ∣ A ∣ ≠ 0 \vert A\vert \not = 0 ∣A∣=0
证明: A 可逆,即有 A − 1 ,使得 A A − 1 = E ∣ A A − 1 ∣ = ∣ A ∣ ∣ A − 1 ∣ = ∣ E ∣ = 1 ∴ ∣ A ∣ ≠ 0 证明:\\ A可逆,即有A^{-1},使得AA^{-1}=E\\ |AA^{-1}|=|A||A^{-1}|=|E|=1\\ \therefore |A|\not=0 证明:A可逆,即有A−1,使得AA−1=E∣AA−1∣=∣A∣∣A−1∣=∣E∣=1∴∣A∣=0
定理2 若 ∣ A ∣ ≠ 0 |A|\not=0 ∣A∣=0,则矩阵A可逆,且
A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{|A|}A^* A−1=∣A∣1A∗
其中 A ∗ A^{*} A∗为矩阵A的伴随矩阵。
证明: 由例 10 知 A A ∗ = A ∗ A = ∣ A ∣ E ∵ ∣ A ∣ ≠ 0 ∴ A A ∗ ∣ A ∣ = A ∗ ∣ A ∣ A = E 按逆矩阵的定义,有矩阵 A 可逆,且 A − 1 = A ∗ ∣ A ∣ 证明:\\ 由例10知\\ AA^{*}=A^{*}A=|A|E\\ \because |A|\not=0\\ \therefore A\frac{A^{*}}{|A|}=\frac{A^{*}}{|A|}A=E\\ 按逆矩阵的定义,有矩阵A可逆,且\\ A^{-1}=\frac{A^{*}}{|A|} 证明:由例10知AA∗=A∗A=∣A∣E∵∣A∣=0∴A∣A∣A∗=∣A∣A∗A=E按逆矩阵的定义,有矩阵A可逆,且A−1=∣A∣A∗
当 ∣ A ∣ = 0 |A|=0 ∣A∣=0时,A称为奇异矩阵。哟路上面两定理知:A是可逆矩阵的充分必要条件是 ∣ A ∣ ≠ 0 |A|\not=0 ∣A∣=0,即可逆矩阵就是非奇异矩阵。
推论 若 A B = E ( 或者 B A = E ) ,则 B = A − 1 AB=E(或者BA=E),则B=A^{-1} AB=E(或者BA=E),则B=A−1
逆矩阵满足下述运算规律:
- 若A可逆,则 A − 1 A^{-1} A−1亦可逆,且 ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A;
- 若A可逆,输入 λ ≠ 0 \lambda\not=0 λ=0,则 λ A \lambda A λA可逆,且 ( λ A ) − 1 = 1 λ A − 1 (\lambda A)^{-1}=\frac{1}{\lambda}A^{-1} (λA)−1=λ1A−1
- 若A、B为同阶矩阵且均可逆,则AB亦可逆,且 ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
- 若A可逆,则 A T A^{T} AT可逆,且 ( A T ) − 1 = ( A − 1 ) T (A^{T})^{-1}=(A^{-1})^{T} (AT)−1=(A−1)T
当A可逆时,还可定义
A 0 = E , A − k = ( A − 1 ) k A^0=E,A^{-k}=(A^{-1})^k A0=E,A−k=(A−1)k
其中k为正整数,这样当A可逆 λ , μ \lambda,\mu λ,μ为整数时,有
A λ A μ = A λ + μ , ( A λ ) μ = A λ μ A^{\lambda}A^{\mu}=A^{\lambda+\mu},(A^{\lambda})^{\mu}=A^{\lambda\mu} AλAμ=Aλ+μ,(Aλ)μ=Aλμ
例11 求二阶矩阵
A = ( a b c d ) A=\begin{pmatrix} a&b\\ c&d \end{pmatrix} A=(acbd)
的逆矩阵。
解: ∣ A ∣ = a d − b c A ∗ = ( d − b − c a ) 当 ∣ A ∣ ≠ 0 使 , A − 1 = 1 ∣ A ∣ A ∗ = 1 a d − b c ( d − b − c a ) 解:\\ |A|=ad-bc\\ A*=\begin{pmatrix} d&-b\\ -c&a \end{pmatrix}\\ 当|A|\not=0使, A^{-1}=\frac{1}{|A|}A^{*}\\ =\frac{1}{ad-bc}\begin{pmatrix} d&-b\\ -c&a \end{pmatrix} 解:∣A∣=ad−bcA∗=(d−c−ba)当∣A∣=0使,A−1=∣A∣1A∗=ad−bc1(d−c−ba)
二、逆矩阵的初步应用
可逆矩阵在线性代数中占有重要的地位,它的应用是多方面的,下面举几个例子。
例13 设
A = ( 1 2 3 2 2 1 3 4 3 ) , B = ( 2 1 5 3 ) , C = ( 1 3 2 0 3 1 ) A=\begin{pmatrix} 1&2&3\\ 2&2&1\\ 3&4&3\\ \end{pmatrix} ,B=\begin{pmatrix} 2&1\\ 5&3\\ \end{pmatrix} ,C=\begin{pmatrix} 1&3\\ 2&0\\ 3&1\\ \end{pmatrix}\\ A= 123224313 ,B=(2513),C= 123301
求矩阵X使其满足 A X B = C AXB=C AXB=C
解: 若 A − 1 , B − 1 存在,则 C = A A − 1 C B − 1 B 有 X = A − 1 C B − 1 ∣ A ∣ = 2 , ∣ B ∣ = 1 , 所以 A − 1 , B − 1 存在 A − 1 = ( 1 3 − 2 − 3 2 − 3 5 2 1 1 − 1 ) , B − 1 = ( 3 − 1 − 5 2 ) X = A − 1 C B − 1 = ( 1 3 − 2 − 3 2 − 3 5 2 1 1 − 1 ) ( 1 3 2 0 3 1 ) ( 3 − 1 − 5 2 ) = ( 1 1 0 − 2 0 2 ) ( 3 − 1 − 5 2 ) = ( − 2 1 10 − 4 − 10 4 ) 解:\\ 若A^{-1},B^{-1}存在,则\\ C=AA^{-1}CB^{-1}B\\ 有X=A^{-1}CB^{-1}\\ |A|=2,|B|=1,所以A^{-1},B^{-1}存在\\ A^{-1}=\begin{pmatrix} 1&3&-2\\ -\frac{3}{2}&-3&\frac{5}{2}\\ 1&1&-1 \end{pmatrix} ,B^{-1}=\begin{pmatrix} 3&-1\\ -5&2\\ \end{pmatrix}\\ X=A^{-1}CB^{-1}= \begin{pmatrix} 1&3&-2\\ -\frac{3}{2}&-3&\frac{5}{2}\\ 1&1&-1 \end{pmatrix} \begin{pmatrix} 1&3\\ 2&0\\ 3&1\\ \end{pmatrix} \begin{pmatrix} 3&-1\\ -5&2\\ \end{pmatrix}\\ =\begin{pmatrix} 1&1\\ 0&-2\\ 0&2 \end{pmatrix} \begin{pmatrix} 3&-1\\ -5&2\\ \end{pmatrix}\\ =\begin{pmatrix} -2&1\\ 10&-4\\ -10&4\\ \end{pmatrix} 解:若A−1,B−1存在,则C=AA−1CB−1B有X=A−1CB−1∣A∣=2,∣B∣=1,所以A−1,B−1存在A−1= 1−2313−31−225−1 ,B−1=(3−5−12)X=A−1CB−1= 1−2313−31−225−1 123301 (3−5−12)= 1001−22 (3−5−12)= −210−101−44
例14 设
P = ( 1 2 1 4 ) , Λ = ( 1 0 0 2 ) , A P = P Λ , 求 A n P=\begin{pmatrix} 1&2\\ 1&4 \end{pmatrix} ,\Lambda=\begin{pmatrix} 1&0\\ 0&2 \end{pmatrix} ,AP=P\Lambda,求A^n P=(1124),Λ=(1002),AP=PΛ,求An
解 : ∣ P ∣ = 2 p − 1 = 1 2 ( 4 − 2 − 1 1 ) A = P Λ P − 1 , A 2 = P Λ P − 1 P Λ P − 1 = P Λ 2 P − 1 , ⋯ , A n = P Λ n P − 1 Λ = = ( 1 0 0 2 ) , Λ 2 = = ( 1 0 0 2 2 ) , ⋯ , Λ n = ( 1 0 0 2 n ) A n = P Λ n P − 1 = ( 1 2 1 4 ) ( 1 0 0 2 n ) 1 2 ( 4 − 2 − 1 1 ) = ( 2 − 2 n 2 n − 1 2 − 2 n + 1 2 n + 1 − 1 ) 解:\\ |P|=2\\ p^{-1}=\frac{1}{2}\begin{pmatrix} 4&-2\\ -1&1\\ \end{pmatrix}\\ A=P\Lambda P^{-1},A^2=P\Lambda P^{-1}P\Lambda P^{-1}=P\Lambda^2 P^{-1},\cdots,A^{n}=P\Lambda^{n} P^{-1}\\ \Lambda==\begin{pmatrix} 1&0\\ 0&2 \end{pmatrix} ,\Lambda^2==\begin{pmatrix} 1&0\\ 0&2^2 \end{pmatrix} ,\cdots,\Lambda^n=\begin{pmatrix} 1&0\\ 0&2^n\\ \end{pmatrix}\\ A^n=P\Lambda^n P^{-1}=\begin{pmatrix} 1&2\\ 1&4 \end{pmatrix} \begin{pmatrix} 1&0\\ 0&2^n\\ \end{pmatrix} \frac{1}{2}\begin{pmatrix} 4&-2\\ -1&1\\ \end{pmatrix}\\ =\begin{pmatrix} 2-2^n&2^n-1\\ 2-2^{n+1}&2^{n+1}-1\\ \end{pmatrix}\\ 解:∣P∣=2p−1=21(4−1−21)A=PΛP−1,A2=PΛP−1PΛP−1=PΛ2P−1,⋯,An=PΛnP−1Λ==(1002),Λ2==(10022),⋯,Λn=(1002n)An=PΛnP−1=(1124)(1002n)21(4−1−21)=(2−2n2−2n+12n−12n+1−1)
设 ϕ ( x ) = a 0 + a 1 x + ⋯ + a m x m 为 x 的 m \phi(x)=a_0+a_1x+\cdots+a_mx^m为x的m ϕ(x)=a0+a1x+⋯+amxm为x的m次多项式,A为 n n n阶矩阵,记
ϕ ( A ) = a 0 E + a 1 A + ⋯ + a m A m \phi(A)=a_0E+a_1A+\cdots+a_mA^m ϕ(A)=a0E+a1A+⋯+amAm
ϕ ( A ) \phi(A) ϕ(A)为矩阵A的m次多项式。
矩阵 A k 、 A l 和 E A^k、A^l和E Ak、Al和E都是可交换的,所以矩阵A的两个多项式 ϕ ( A ) 和 f ( A ) \phi(A)和f(A) ϕ(A)和f(A)也是可交换的,即总有
ϕ ( A ) f ( A ) = f ( A ) ϕ ( A ) \phi(A)f(A)=f(A)\phi(A) ϕ(A)f(A)=f(A)ϕ(A)
从而A的几个多项式可以像数 x x x的多项式一样相乘或者分解因式。
-
如果 A = P Λ P − 1 ,则 A k = P Λ k P − 1 A=P\Lambda P^{-1},则A^k=P\Lambda^kP^{-1} A=PΛP−1,则Ak=PΛkP−1,从而 ϕ ( A ) = P a 0 E P − 1 + P a 1 Λ P − 1 + ⋯ + P a m Λ m P − 1 = P ϕ ( Λ ) P − 1 \phi(A)=Pa_0EP^{-1}+Pa_1\Lambda P^{-1}+\cdots+Pa_m\Lambda^mP^{-1}=P\phi(\Lambda)P^{-1} ϕ(A)=Pa0EP−1+Pa1ΛP−1+⋯+PamΛmP−1=Pϕ(Λ)P−1
-
如果 Λ = d i a g ( λ 1 , λ 2 , ⋯ , λ n ) \Lambda=diag(\lambda_1,\lambda_2,\cdots,\lambda_n) Λ=diag(λ1,λ2,⋯,λn)为对角矩阵,则 Λ k = d i a g ( λ 1 k , λ 2 k , ⋯ , λ n k ) \Lambda^k=diag(\lambda_1^k,\lambda_2^k,\cdots,\lambda_n^k) Λk=diag(λ1k,λ2k,⋯,λnk),从而
ϕ ( Λ ) = a 0 E + a 1 Λ + ⋯ + a m Λ m = d i a g ( ϕ ( λ 1 ) , ϕ ( λ 2 ) , ⋯ , ϕ ( λ n ) ) \phi(\Lambda)=a_0E+a_1\Lambda+\cdots+a_m\Lambda^m\\ =diag(\phi(\lambda_1),\phi(\lambda_2),\cdots,\phi(\lambda_n)) ϕ(Λ)=a0E+a1Λ+⋯+amΛm=diag(ϕ(λ1),ϕ(λ2),⋯,ϕ(λn))
例15 设
P = ( − 1 1 1 1 0 2 1 1 − 1 ) , Λ = ( 1 2 − 3 ) , A P = P Λ P=\begin{pmatrix} -1&1&1\\ 1&0&2\\ 1&1&-1 \end{pmatrix} ,\Lambda=\begin{pmatrix} 1&&\\ &2&\\ &&-3 \end{pmatrix} ,AP=P\Lambda\\ P= −11110112−1 ,Λ= 12−3 ,AP=PΛ
求 ϕ ( A ) = A 3 + 2 A 2 − 3 A \phi(A)=A^3+2A^2-3A ϕ(A)=A3+2A2−3A
解: ∣ P ∣ = 6 A = P Λ P − 1 ϕ ( A ) = P ϕ ( Λ ) P − 1 , ϕ ( Λ ) = d i a g ( ϕ ( λ 1 k ) , ϕ ( λ 2 ) k , ⋯ , ϕ ( λ n k ) ) ϕ ( 1 ) = 0 , ϕ ( 2 ) = 10 , ϕ ( − 3 ) = 0 ϕ ( A ) = P ϕ ( Λ ) P − 1 = ( − 1 1 1 1 0 2 1 1 − 1 ) ( 0 10 0 ) 1 ∣ P ∣ P ∗ 5 ( 1 0 1 0 0 0 1 0 1 ) 解:\\ |P|=6\\ A=P\Lambda P^{-1}\\ \phi(A)=P\phi(\Lambda) P^{-1},\phi(\Lambda)=diag(\phi(\lambda_1^k),\phi(\lambda_2)^k,\cdots,\phi(\lambda_n^k))\\ \phi(1)=0,\phi(2)=10,\phi(-3)=0\\ \phi(A)=P\phi(\Lambda)P^{-1}=\begin{pmatrix} -1&1&1\\ 1&0&2\\ 1&1&-1 \end{pmatrix} \begin{pmatrix} 0&&\\ &10&\\ &&0\\ \end{pmatrix} \frac{1}{|P|}P^*\\ 5\begin{pmatrix} 1&0&1\\ 0&0&0\\ 1&0&1\\ \end{pmatrix} 解:∣P∣=6A=PΛP−1ϕ(A)=Pϕ(Λ)P−1,ϕ(Λ)=diag(ϕ(λ1k),ϕ(λ2)k,⋯,ϕ(λnk))ϕ(1)=0,ϕ(2)=10,ϕ(−3)=0ϕ(A)=Pϕ(Λ)P−1= −11110112−1 0100 ∣P∣1P∗5 101000101
结语
❓QQ:806797785
⭐️文档笔记地址 https://github.com/gaogzhen/math
参考:
[1]同济大学数学系.工程数学.线性代数 第6版 [M].北京:高等教育出版社,2014.6.p39-44.
[2]同济六版《线性代数》全程教学视频[CP/OL].2020-02-07.p10.
相关文章:

0203逆矩阵-矩阵及其运算-线性代数
文章目录 一、逆矩阵的定义、性质和求法二、逆矩阵的初步应用结语 一、逆矩阵的定义、性质和求法 定义7 对于 n n n阶矩阵A,如果有一个 n n n阶矩阵B,使 A B B A E ABBAE ABBAE 则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆…...
加州大学欧文分校英语基础语法专项课程03:Simple Past Tense 学习笔记(完结)
Learn English: Beginning Grammar Specialization Specialization Certificate course 3: Simple Past Tense Course Certificate 本文是学习 https://www.coursera.org/learn/simple-past-tense 这门课的学习笔记,如有侵权,请联系删除。…...
基于Java微信小程序的医院挂号小程序,附源码
博主介绍:✌IT徐师兄、7年大厂程序员经历。全网粉丝15W、csdn博客专家、掘金/华为云//InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇dz…...

7.网络编程-安全
目录 引言 Session Cookie JWT (JSON Web Token) 网络攻击 CSRF DDoS 其他常见网络攻击类型及应对措施 引言 Session、Cookie 和 JWT 都是Web开发中用于实现用户状态管理和身份验证的技术。它们各自有不同的特点和应用场景: Session Session 是一种服务器…...

信息泄露漏洞的JS整改方案
引言 🛡️ 日常工作中,我们经常会面临线上环境被第三方安全厂商扫描出JS信息泄露漏洞的情况,这给我们的系统安全带来了潜在威胁。但幸运的是,对于这类漏洞的整改并不复杂。本文将介绍几种可行的整改方法,以及其中一种…...

WKWebView的使用
一、简介 在iOS中,WKWebView是WebKit框架提供的一个用于展示网页内容的控件,相比UIWebView有更好的性能和功能。 以下是在iOS中使用WKWebView的基本步骤: 1.1 导入WebKit框架 import WebKit1.2 创建WKWebView实例 let webView WKWebVie…...

iOS MT19937随机数生成,结合AES-CBC加密算法实现。
按处理顺序说明: 1. 生成随机数序列字符串函数 生成方法MT19937,初始种子seed,利用C库方法,生成: #include <random> //C 库头文件引入NSString * JKJMT19937Seed(uint32_t seed) {NSLog("MT19937Seed种…...

阿里云2024年优惠券获取方法及使用教程详解
阿里云是阿里巴巴集团旗下的云计算服务提供商,是全球领先的云计算及人工智能科技公司之一。提供免费试用、云服务器、云数据库、云安全、云企业应用等云计算服务,以及大数据、人工智能服务、精准定制基于场景的行业解决方案。 阿里云2024年优惠券的获取方…...

hadoop中hdfs的fsimage文件与edits文件
hadoop中hdfs的fsimage文件与edits文件的作用 首先,我们抛出fsimage和edits文件的功能描述。 Fsimage文件: HDFS文件系统元数据的一个永久性的检查点,其中包含HDFS文件系统的 所有目录和文件inode的序列化信息。 Edits文件:存放HDFS文件系统的所有更…...

最新版两款不同版SEO超级外链工具PHP源码
可根据个人感觉喜好自行任意选择不同版本使用(版V1或版V2) 请将zip文件全部解压缩即可访问! 源码全部开源,支持上传二级目录访问 已更新增加大量高质量外链(若需要增加修改其他外链请打开txt文件)修复优…...

.net框架和c#程序设计第二次测试
一、实验内容 1、设计一个用户登录页面webform1.aspx,效果如下图所示: 2、点击webform1.aspx中“还未注册”连接进入register.aspx,注册页面效果如下图所示:点击用户注册信息到usershow.aspx页面,并显示注册的用户信息…...
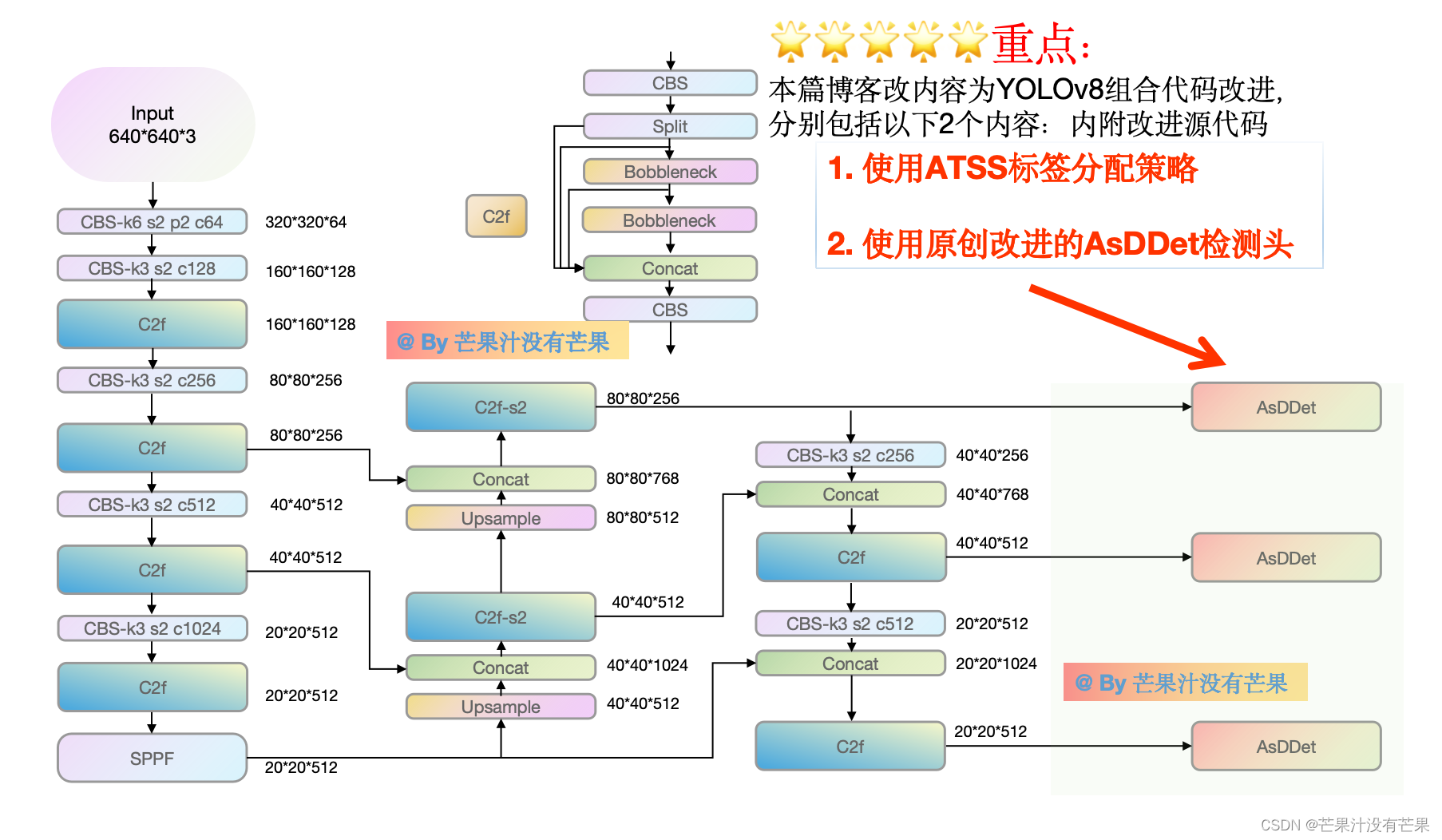
芒果YOLOv8改进组合157:动态标签分配ATSS+新颖高效AsDDet检测头组合改进,共同助力VisDrone涨点1.8%,小目标高效涨点
💡本篇内容:【芒果YOLOv8改进ATSS标签分配策略|第三集】芒果YOLOv8改进组合157:动态标签分配ATSS+新颖高效AsDDet检测头组合改进,共同助力VisDrone涨点1.8%,小目标高效涨点 💡🚀🚀🚀本博客 标签分配策略ATSS改进+ 新颖高效AsDDet检测头组合改进,适用于 YOLOv8 …...

自媒体内容创作助手:7款必备ai写作工具一览! #学习方法#科技#其他
这些工具不仅可以快速生成高质量的文本内容,还可以根据用户的需求进行个性化定制。它们可以帮助我们节省大量的时间和精力,让我们更加专注于创意和细节的打磨。本文将为大家详细介绍几个AI写作工具,让你在写作领域更上一层楼。 1.七燕写作 这…...

文心一言 vs GPT-4 -- 全面横向比较
文心一言和GPT-4都是当前非常先进的自然语言处理模型,它们在语言理解、生成和翻译等方面都展现出了出色的能力。以下是对这两个模型的全面横向比较: 核心技术基础: 文心一言:是基于BERT(Bidirectional Encoder Repre…...

Leetcode C语言习题
Leetcode习题27:移除元素 题目: 说明: 示例: 题解: 方法一:(开辟额外的数组空间) 我们可以创建一个新的数组,然后用循环来遍历原数组,将原数组中不为 val…...
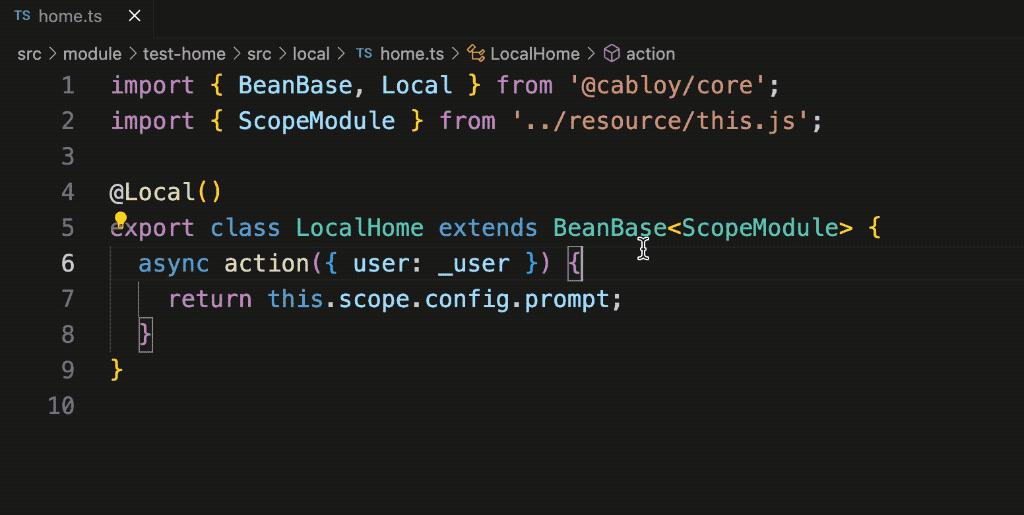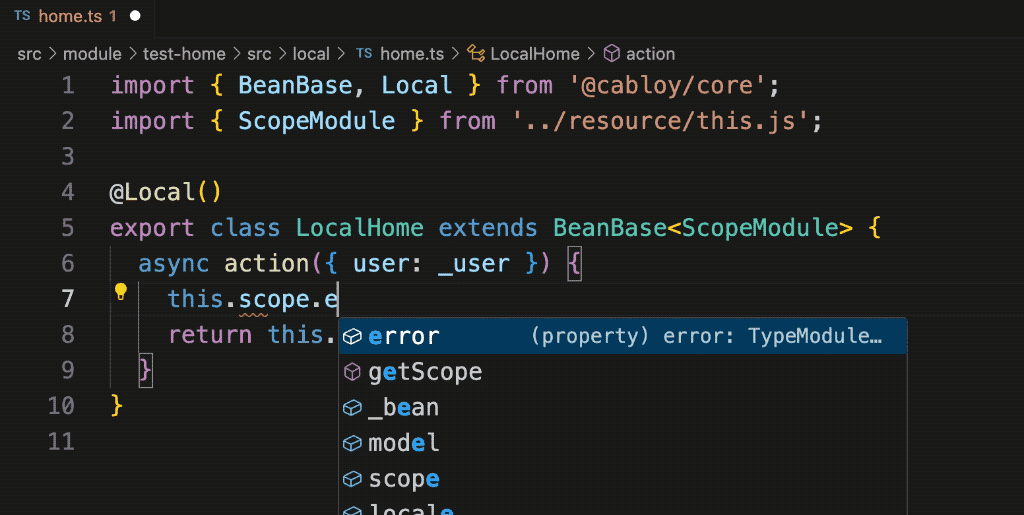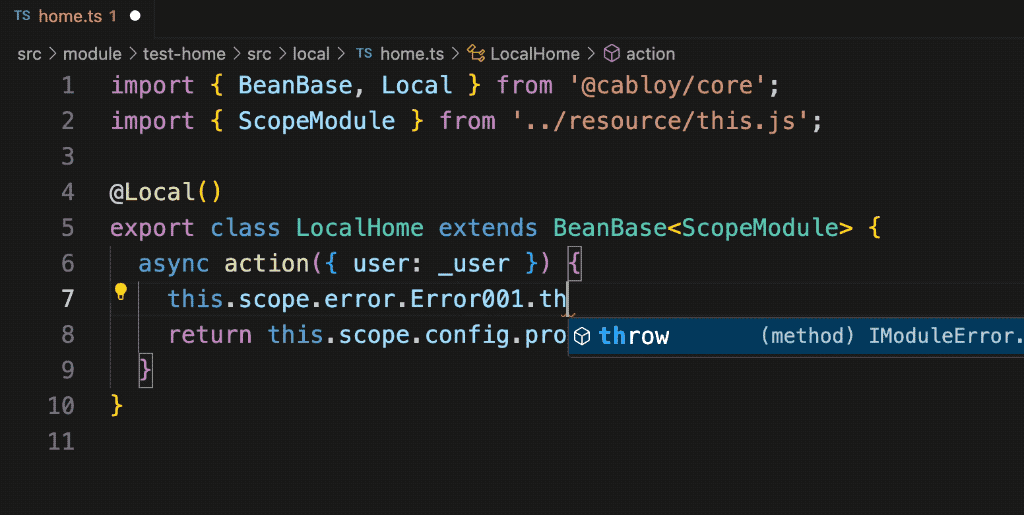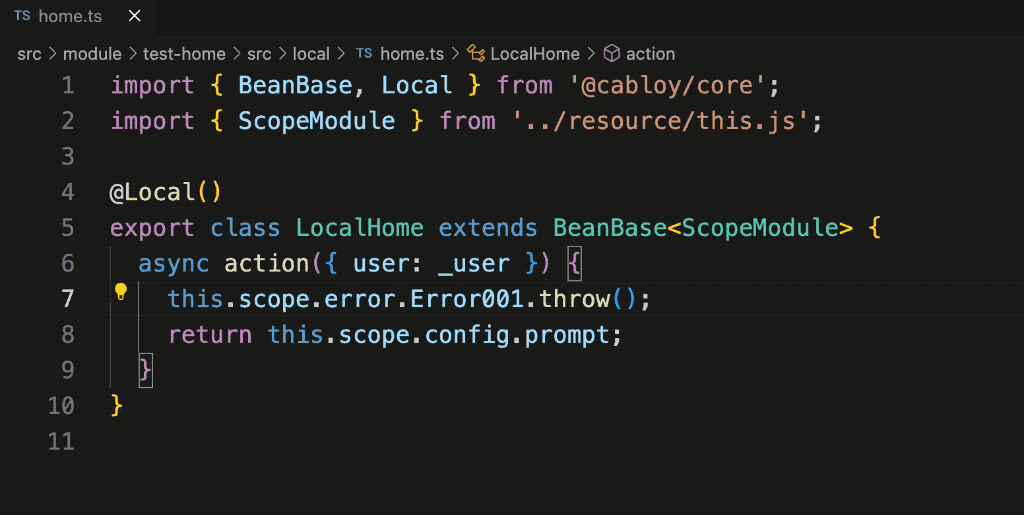
比 Nest.js 更优雅的 TS 控制反转策略 - 依赖查找
一、Cabloy5.0 内测预告 Cabloy5.0 采用 TS 对整个全栈框架进行了脱胎换骨般的大重构,并且提供了更加优雅的 ts 控制反转策略,让我们的业务开发更加快捷顺畅 1. 新旧技术栈对比: 后端前端旧版js、egg2.0、mysqljs、vue2、framework7新版ts…...

java算法day43 | 动态规划part05 ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的…...

STM32无刷电机全套开发资料(源码、原理图、PCB工程及说明文档)
目录 1、原理图、PCB、BOOM表 2、设计描述 2.1 前言 2.2 设计电路规范 3、代码 4、资料清单 资料下载地址:STM32无刷电机全套开发资料(源码、原理图、PCB工程及说明文档) 1、原理图、PCB、BOOM表 2、设计描述 2.1 前言 经过一个星期的画PCB,今…...

工地安全监测识别摄像机
工地安全监测识别摄像机是一种在建筑工地和施工现场广泛使用的智能监控设备,主要用于监测施工过程中可能出现的安全隐患和违规行为,以确保工地人员和设备的安全。通过高清摄像头、智能算法和远程监控系统的结合,该摄像机可以实时监测工地各个…...
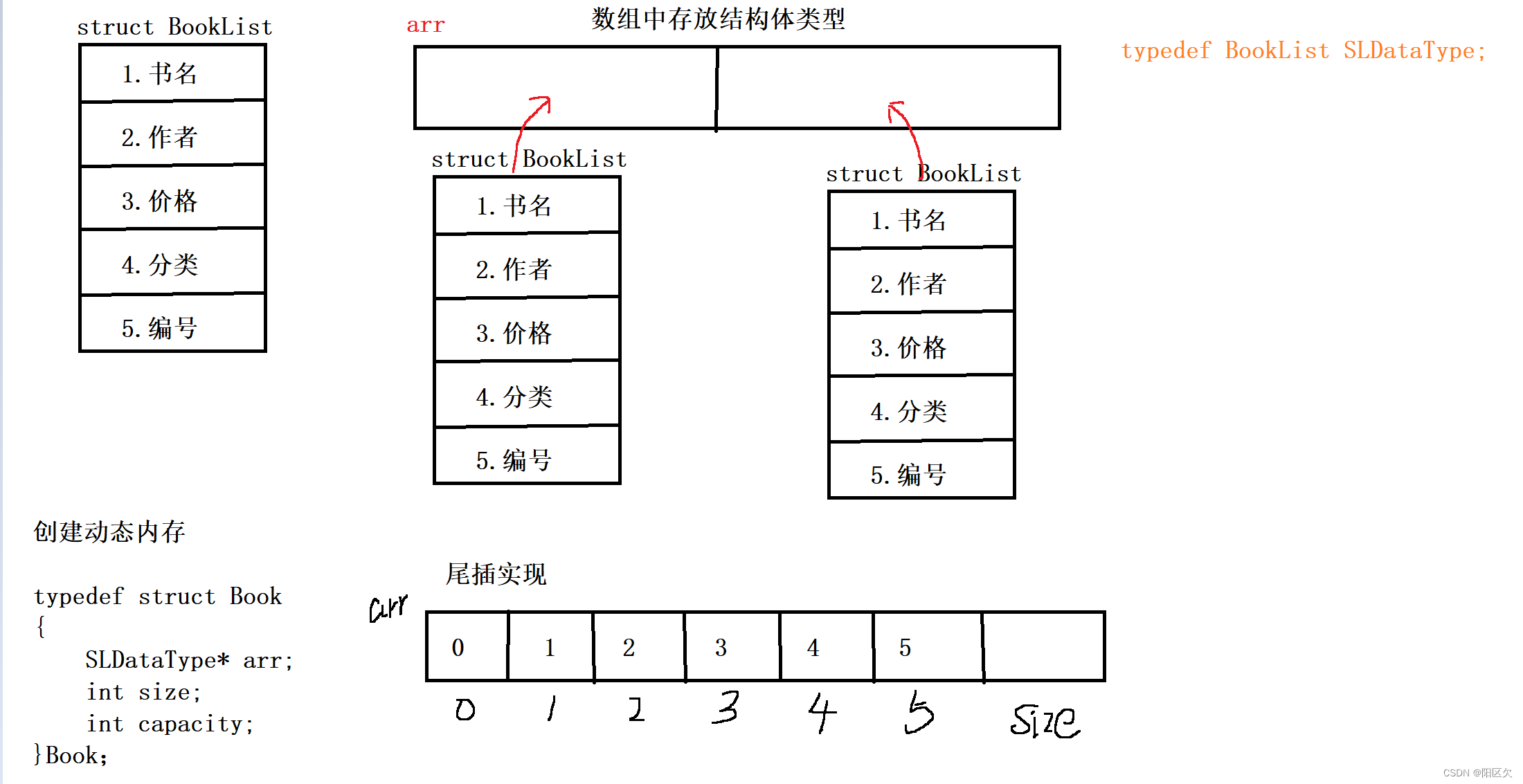
【零基础学数据结构】顺序表实现书籍存储
目录 书籍存储的实现规划 编辑 前置准备: 书籍结构体: 书籍展示的初始化和文件加载 书籍展示的销毁和文件保存 书籍展示的容量检查 书籍展示的尾插实现 书籍展示的书籍增加 书籍展示的书籍打印 书籍删除展示数据 书籍展示修改数据 在指定位置之前…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
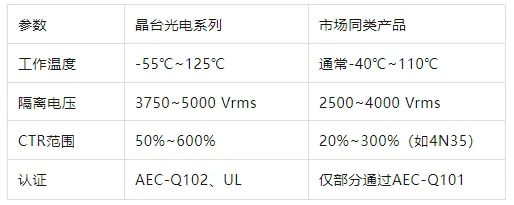
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
