java算法day43 | 动态规划part05 ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II


核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
class Solution {public int lastStoneWeightII(int[] stones) {int sum=0;for(int i=0;i<stones.length;i++){sum+=stones[i];}int target=sum/2;int dp[]=new int[target+1];//1、定义dp数组 3、第一列初始化为0for(int i=0;i<stones.length;i++){for(int j=target;j>=stones[i];j--){//4、遍历顺序dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);//2.递推公式}}return sum-dp[target]-dp[target];//最终的返回结果}
}
时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
空间复杂度:O(m)
494. 目标和


思路: 这道题的dp数组的含义变了。具体看代码随想录的讲解
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int i=0;i<nums.length;i++){sum+=nums[i];}//如果不能满足(target+sum)/2为整数的条件或target的绝对值大于sum的绝对值,直接返回0if((target+sum)%2!=0 || Math.abs(target)>Math.abs(sum)) return 0;int size=(target+sum)/2;int[] dp=new int[size+1];//1、定义dp数组,表示j容量时的表达式数目dp[0]=1;//3、初始化for(int i=0;i<nums.length;i++){for(int j=size;j>=nums[i];j--){//4、因为是01背包,所以反向遍历dp[j]=dp[j]+dp[j-nums[i]];//2、递推公式}}return dp[size];}
}
时间复杂度:O(n × m),n为正数个数,m为背包容量
空间复杂度:O(m),m为背包容量
474.一和零

思路: 这道题是一个二维的背包问题,和普通的背包相比只需要多一层对容量的循环。

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp=new int[m+1][n+1];//1、定义dp数组,表示当0的容量为x,1的容量为n时,最大子集的长度for(int i=0;i<strs.length;i++){//4、遍历顺序,物品正序遍历int weightm=0;int weightn=0;for(int j=0;j<strs[i].length();j++){if(strs[i].charAt(j)=='0') weightm++; else weightn++;}for(int x=m;x>=weightm;x--){//4、物品的空间占用逆序遍历for(int y=n;y>=weightn;y--){dp[x][y]=Math.max(dp[x][y],dp[x-weightm][y-weightn]+1);//2、递推公式,注意value是1}}}return dp[m][n];}
}
时间复杂度: O(kmn),k 为strs的长度
空间复杂度: O(mn)
相关文章:

java算法day43 | 动态规划part05 ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的…...

STM32无刷电机全套开发资料(源码、原理图、PCB工程及说明文档)
目录 1、原理图、PCB、BOOM表 2、设计描述 2.1 前言 2.2 设计电路规范 3、代码 4、资料清单 资料下载地址:STM32无刷电机全套开发资料(源码、原理图、PCB工程及说明文档) 1、原理图、PCB、BOOM表 2、设计描述 2.1 前言 经过一个星期的画PCB,今…...

工地安全监测识别摄像机
工地安全监测识别摄像机是一种在建筑工地和施工现场广泛使用的智能监控设备,主要用于监测施工过程中可能出现的安全隐患和违规行为,以确保工地人员和设备的安全。通过高清摄像头、智能算法和远程监控系统的结合,该摄像机可以实时监测工地各个…...
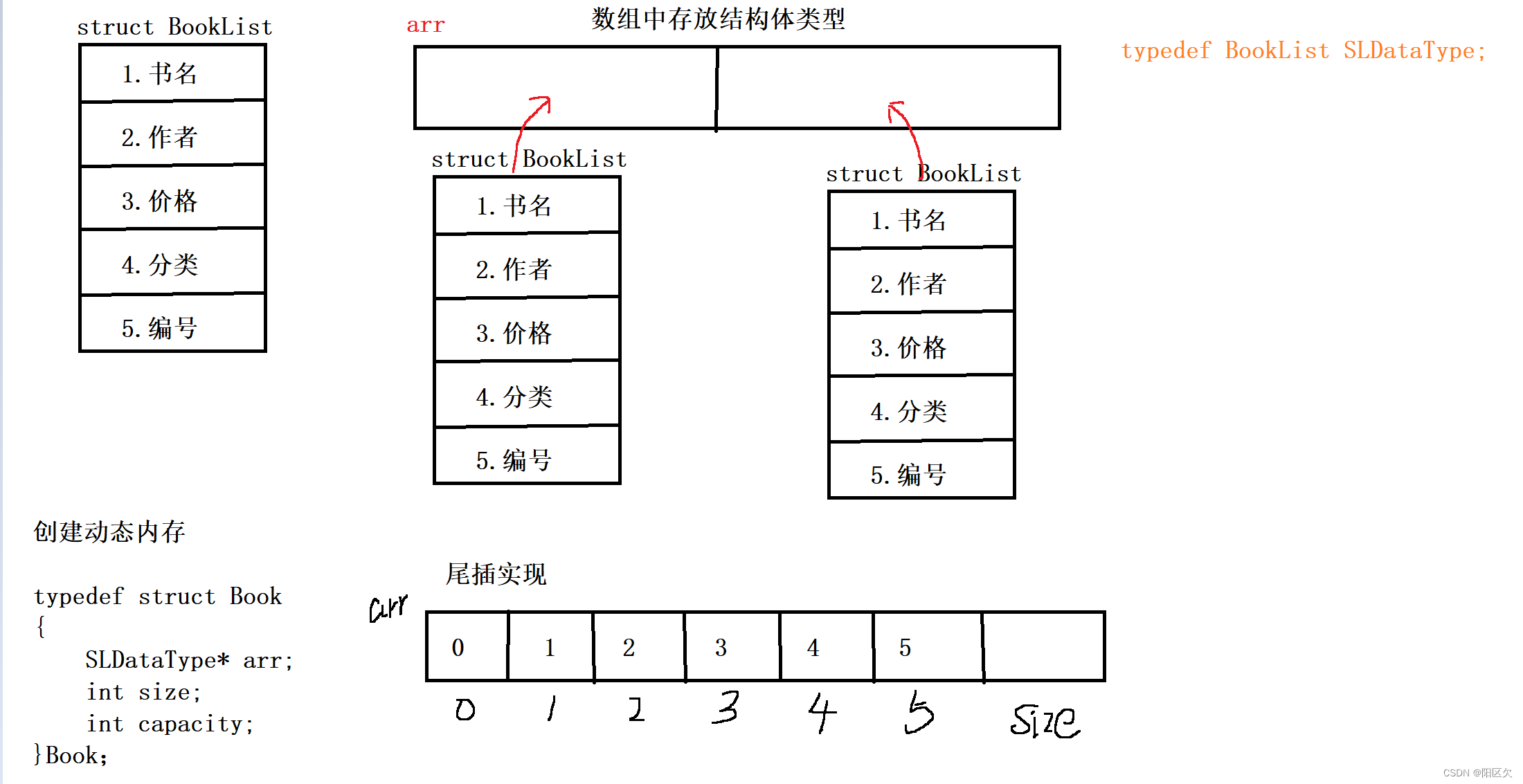
【零基础学数据结构】顺序表实现书籍存储
目录 书籍存储的实现规划 编辑 前置准备: 书籍结构体: 书籍展示的初始化和文件加载 书籍展示的销毁和文件保存 书籍展示的容量检查 书籍展示的尾插实现 书籍展示的书籍增加 书籍展示的书籍打印 书籍删除展示数据 书籍展示修改数据 在指定位置之前…...
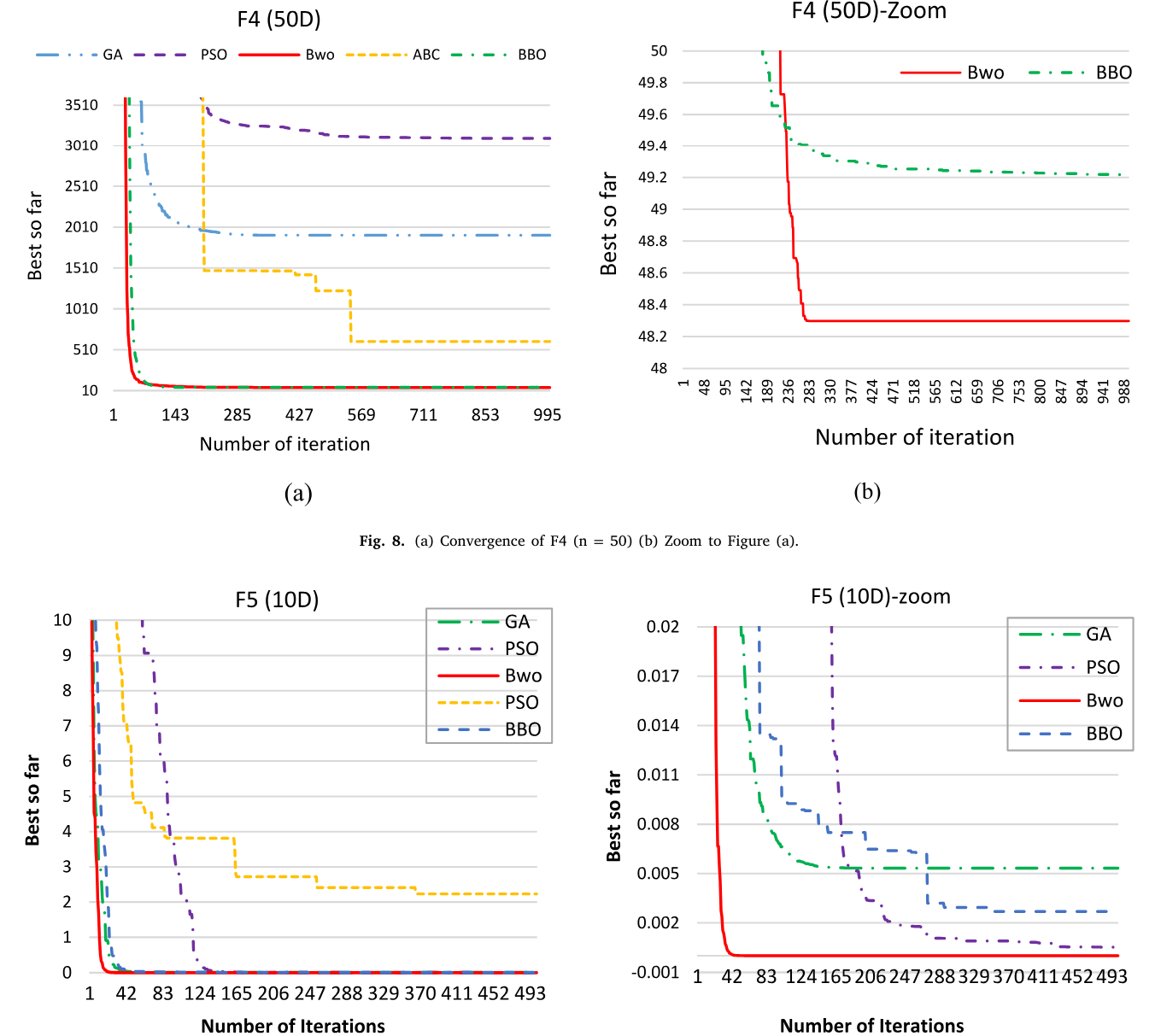
【智能算法】黑寡妇优化算法(BWO)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2020年,V Hayyolalam等人受到自然界黑寡妇交配行为启发,提出了黑寡妇优化算法(Black Widow Optimization Agorithm, BWO)。 2.算法原理 2.1算法思想…...

C#-非托管代码
非托管代码是指不受.NET运行时(CLR)的管理和控制,而是直接由操作系统或其他本机执行环境(如C/C编译的代码)所执行的代码。以下是一些常见的非托管代码的例子: C/C代码:通过使用C或C等编程语言编…...

计算机视觉之三维重建(7)---多视图几何(下)
文章目录 一、透视结构恢复问题1.1 概述1.2 透视结构恢复歧义1.3 代数方法1.4 捆绑调整 二、P3P问题三、随机采样一致性 一、透视结构恢复问题 1.1 概述 1. 透视结构恢复问题:摄像机为透视相机,内外参数均未知。 2. 问题:已知 n n n 个三维…...
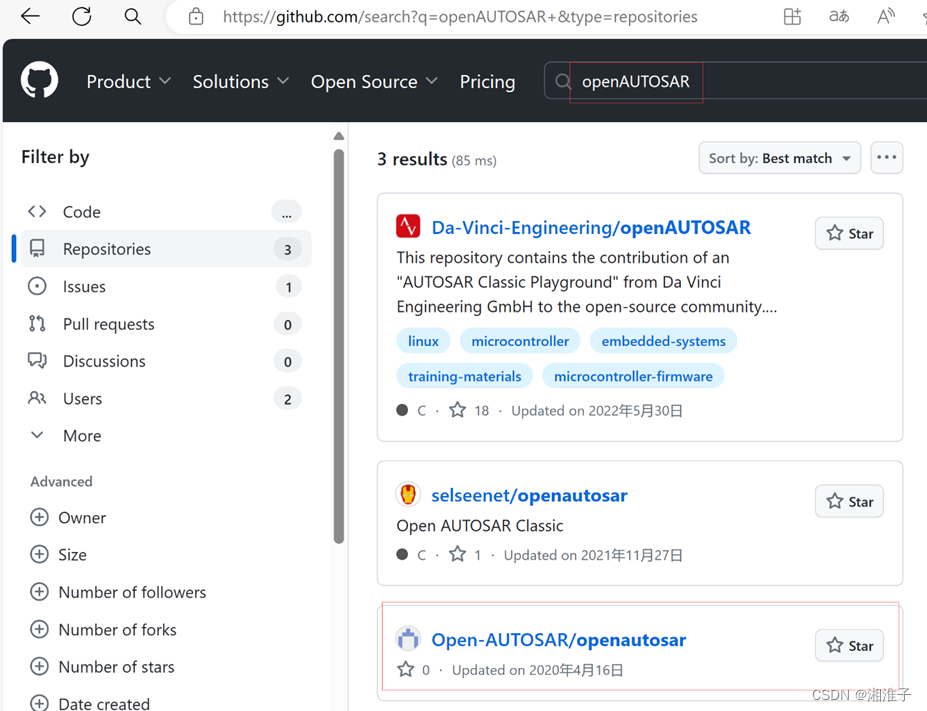
AUTOSAR配置工具开发教程 - 开篇
简介 本系列的教程,主要讲述如何自己开发一套简单的AUTOSAR ECU配置工具。适用于有C# WPF基础的人员。 简易介绍见:如何打造AUTOSAR工具_autosar_mod_ecuconfigurationparameters-CSDN博客 实现版本 AUTOSAR 4.0.3AUTOSAR 4.2.2AUTOSAR 4.4.0 效果 …...
配置VM开机自启动
1. 在此电脑-右键选择“管理”-服务和应用程序-服务中找到VMware Workstation Server服务(新版名称也可能是VMware自启动服务,自己找一下,服务属性里有描述信息的),将其启用并选择开机自动启动 新版参考官方文档&…...
工作的第四天
推荐一个软件分配软件 我们看一下如何使用 连接信息 AOC中国官方网站 发现打开 还是这个页面信息,发现最后出现了页面重新定向的问题 我服了 我的码 怎么解决 我想用这个软件 来看看这个软件下载就可以使用 一听到钱我使用的情绪不是很高了 算了不使用 使用…...

前端开发语言概览:从HTML、CSS到JavaScript
随着互联网的发展,前端开发领域涌现出了许多不同的编程语言和技术,用于构建各种类型的网页和应用程序。本文将介绍几种主流的前端开发语言,包括 HTML、CSS 和 JavaScript,并简要讨论它们在前端开发中的作用和特点。 1. HTML&…...

《Java面试自救指南》(专题二)计算机网络
文章目录 力推的计网神课get请求和post请求的区别在浏览器网址输入一个url后直到浏览器显示页面的过程常用状态码session 和 cookie的区别TCP的三次握手和四次挥手七层OSI模型(TCP/IP协议模型)各种io模型的知识http协议和tcp协议的区别https和http的区别…...
)
Android14音频进阶之<进阶调试>:Perfetto定位系统音频问题(六十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒体系统工程师系列【原创干货持续更新中……】🚀 优质视频课程:AAOS车载系统+AOSP…...
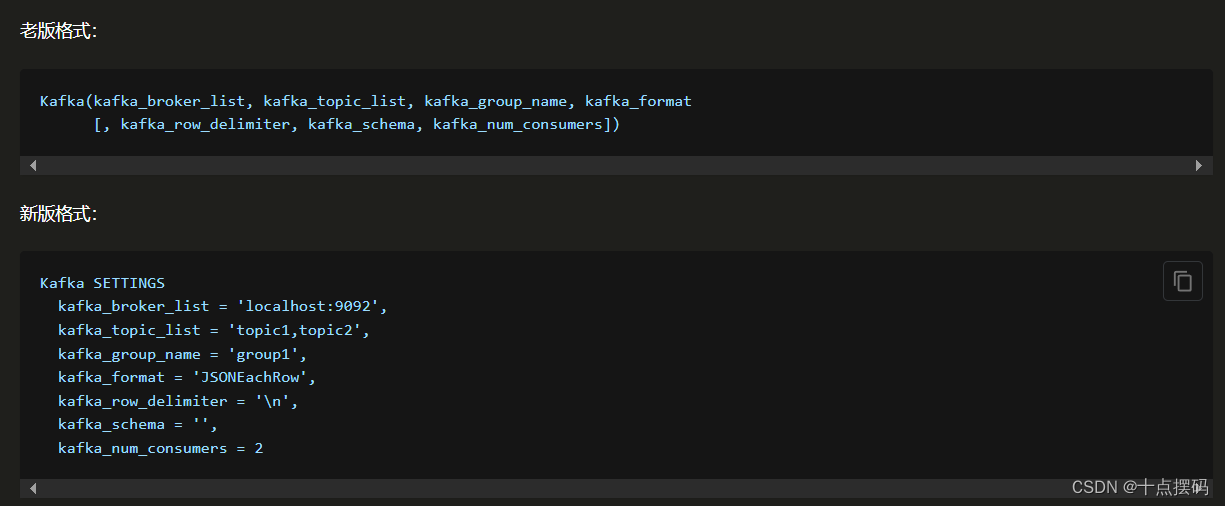
使用 Clickhouse 集成的表引擎同步数据方式详解
Clickhouse作为一个列式存储分析型数据库,提供了很多集成其他组件的表引擎数据同步方案。 官网介绍 一 Kafka 表引擎 使用Clickhouse集成的Kafka表引擎消费Kafka写入Clickhouse表中。 1.1 流程图 1.2 建表 根据上面的流程图需要建立三张表,分别Click…...
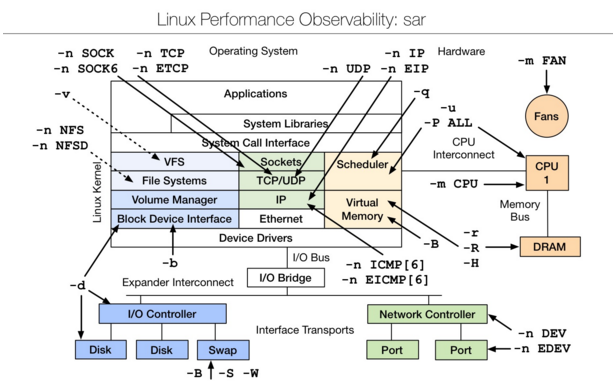
Linux 性能分析工具大全
vmstat--虚拟内存统计 vmstat(VirtualMeomoryStatistics,虚拟内存统计)是 Linux 中监控内存的常用工具,可对操作系统的虚拟内存、进程、CPU 等的整体情况进行监视。vmstat 的常规用法:vmstat interval times 即每隔 interval 秒采…...

FME学习之旅---day21
我们付出一些成本,时间的或者其他,最终总能收获一些什么。 教程:AutoCAD 变换 相关的文章 为您的 DWG 赋予一些样式:使用 DWGStyler、模板文件、块等 FME数据检查器在显示行的方式上受到限制。它只能显示线条颜色,而…...
volta(轻松切换管理Node.js版本)
Node.js版本管理 Volta提供了一个简单直观的命令行界面,可以轻松地安装、卸载、更新和切换Node.js版本。 Volta 既可以全局使用,也可以在项目级别使用,可以为每个项目单独设置node版本,nvm不行。 下载安装Volta 参考: …...

机器学习知识点
1鸢尾花分类 鸢尾花分类问题是一个经典的机器学习问题,旨在根据鸢尾花的花萼长度、花萼宽度、花瓣长度和花瓣宽度等特征,将鸢尾花分成三个品种:山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚…...

SQL注入利用学习-Union联合注入
联合注入的原理 在SQL语句中查询数据时,使用select 相关语句与where 条件子句筛选符合条件的记录。 select * from person where id 1; #在person表中,筛选出id1的记录如果该id1 中的1 是用户可以控制输入的部分时,就有可能存在SQL注入漏洞…...

zookeeper源码(12)命令行客户端
zkCli.sh脚本 这个命令行脚本在bin目录下: ZOOBIN"${BASH_SOURCE-$0}" ZOOBIN"$(dirname "${ZOOBIN}")" ZOOBINDIR"$(cd "${ZOOBIN}"; pwd)"# 加载zkEnv.sh脚本 if [ -e "$ZOOBIN/../libexec/zkEnv.sh&qu…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
