计算机视觉之三维重建(7)---多视图几何(下)
文章目录
- 一、透视结构恢复问题
- 1.1 概述
- 1.2 透视结构恢复歧义
- 1.3 代数方法
- 1.4 捆绑调整
- 二、P3P问题
- 三、随机采样一致性
一、透视结构恢复问题
1.1 概述
1. 透视结构恢复问题:摄像机为透视相机,内外参数均未知。
2. 问题:已知 n n n 个三维点 X j X_j Xj 在 m m m 张图像中的对应点的像素坐标为 x i j x_{ij} xij,且 x i j = M i X j x_{ij}=M_iX_j xij=MiXj,其中 M i M_i Mi 为第 i i i 张图片对应的摄像机投影矩阵,求解 n n n 个三维点 X j X_j Xj 的坐标以及 m m m 个摄像机投影矩阵 M i M_i Mi。

1.2 透视结构恢复歧义
1. 透视结构与仿射结构的区别在于,透视结构计算得到的投影矩阵 M i M_i Mi,与真实投影矩阵差一个 4 ∗ 4 4*4 4∗4 的可逆矩阵 H H H,也就是差了一个透视变换关系。

2. 对于给定 m m m 个相机, n n n 个三维点,我们将有 2 m n 2mn 2mn 个等式, 11 m + 3 n − 15 11m+3n-15 11m+3n−15 个未知量。

1.3 代数方法
1. 求解步骤:(1) 求解基础矩阵 F F F (归一化八点法)。 (2) 基于 F F F 估计摄像机矩阵 F → M 1 , M 2 F \rightarrow M_1,M_2 F→M1,M2。 (3) 三角化。
关键是第二步的求解。
2. (1)令 M 1 ∗ = [ I ∣ 0 ] M_1^*=[I|0] M1∗=[I∣0], M 2 ∗ = [ A ∣ b ] M_2^*=[A|b] M2∗=[A∣b]。推导出基础矩阵 F F F 与 A A A 和 b b b 的关系: F = [ b x ] A F=[b_x]A F=[bx]A。注:同方向的向量叉乘为 0 0 0。

(2)如何计算 A A A 和 b b b:

1.4 捆绑调整
1. 捆绑调整(Bundle Adjustment):捆绑调整使用最小化重投影误差,可以进行多次迭代,使重构点足够拟合真实值,可以应用于欧式结构、仿射结构和透视结构多种情况,是一个恢复结构和运动的非线性方法。
2. 代数法与分解法的局限性:(1) 因式分解法:假定所有点都是可见的,所以对于存在遮挡,建立对应点关系失败的情况将不得不删除该对应点关系。 (2) 代数法:应用于 2 2 2 视图重建,多视图容易出现误差累积。
3. 最小化重投影误差: m i n ( E ( M , X ) ) = ∑ i = 1 m ∑ j = 1 n D ( x i j , M i X j ) 2 min(E(M,X))=\sum_{i=1}^m \sum_{j=1}^nD(x_{ij},M_iX_j)^2 min(E(M,X))=∑i=1m∑j=1nD(xij,MiXj)2

4. 捆绑调整的优势:同时处理大量视图,处理丢失的数据。局限性:大量参数的最小化问题,需要良好的初始条件(即初始 M i M_i Mi)。一般来说,捆绑调整作为运动恢复问题的最后一步,首先通过分解或代数方法先求出优化问题的初始 M i M_i Mi。
二、P3P问题
1. (1) PnP 问题:指通过世界中 N N N 个三维点坐标及其在图像中 N N N 个像点坐标,计算出相机或物体位姿的问题。 (2) P3P 问题:我们只讨论世界中 3 3 3 个三维点和图像中 3 3 3 个像点的关系,计算欧式结构恢复相机位姿的问题,也就是计算出摄像机的外参数 R R R、 T T T。 (3) 相比于之前求 F F F 和三角化得到摄像机外参数的方法,该方法误差更小。
2. P3P 问题解法如下所示。其中步骤 1 1 1 的计算方法:由于 a = K [ I 0 ] P a a=K[I \hspace{0.2cm} 0]P_a a=K[I0]Pa,则 K − 1 a = [ I 0 ] P a K^{-1}a=[I \hspace{0.2cm} 0]P_a K−1a=[I0]Pa,所极点到像点 a a a 的方向向量为: o a → = K − 1 a ∣ ∣ K − 1 a ∣ ∣ \overrightarrow{oa}=\frac{K^{-1}a}{||K^{-1}a||} oa=∣∣K−1a∣∣K−1a,同理可以计算出 o b → \overrightarrow{ob} ob 和 o c → \overrightarrow{oc} oc。


三、随机采样一致性
1. 随机采样(Random sample consensus):一种适用于数据受到异常值污染的模型拟合方法,通过选择随机均匀采样一定的点,估计模型参数,并输出模型分数最高的模型。
2. 算法流程:
(1) 随机均匀采样获取模型求解所需的最小子集。
(2) 适用该子集估计模型参数。
(3) 计算剩余样本与当前模型的一致性,统计满足当前模型的内点(在正确拟合模型上的点为内点,负样本点为外点)个数,作为当前模型分数。
(4) 按照设定次数重复(1)-(3)步,最终输出分数最高的模型。

相关文章:

计算机视觉之三维重建(7)---多视图几何(下)
文章目录 一、透视结构恢复问题1.1 概述1.2 透视结构恢复歧义1.3 代数方法1.4 捆绑调整 二、P3P问题三、随机采样一致性 一、透视结构恢复问题 1.1 概述 1. 透视结构恢复问题:摄像机为透视相机,内外参数均未知。 2. 问题:已知 n n n 个三维…...
AUTOSAR配置工具开发教程 - 开篇
简介 本系列的教程,主要讲述如何自己开发一套简单的AUTOSAR ECU配置工具。适用于有C# WPF基础的人员。 简易介绍见:如何打造AUTOSAR工具_autosar_mod_ecuconfigurationparameters-CSDN博客 实现版本 AUTOSAR 4.0.3AUTOSAR 4.2.2AUTOSAR 4.4.0 效果 …...
配置VM开机自启动
1. 在此电脑-右键选择“管理”-服务和应用程序-服务中找到VMware Workstation Server服务(新版名称也可能是VMware自启动服务,自己找一下,服务属性里有描述信息的),将其启用并选择开机自动启动 新版参考官方文档&…...
工作的第四天
推荐一个软件分配软件 我们看一下如何使用 连接信息 AOC中国官方网站 发现打开 还是这个页面信息,发现最后出现了页面重新定向的问题 我服了 我的码 怎么解决 我想用这个软件 来看看这个软件下载就可以使用 一听到钱我使用的情绪不是很高了 算了不使用 使用…...

前端开发语言概览:从HTML、CSS到JavaScript
随着互联网的发展,前端开发领域涌现出了许多不同的编程语言和技术,用于构建各种类型的网页和应用程序。本文将介绍几种主流的前端开发语言,包括 HTML、CSS 和 JavaScript,并简要讨论它们在前端开发中的作用和特点。 1. HTML&…...

《Java面试自救指南》(专题二)计算机网络
文章目录 力推的计网神课get请求和post请求的区别在浏览器网址输入一个url后直到浏览器显示页面的过程常用状态码session 和 cookie的区别TCP的三次握手和四次挥手七层OSI模型(TCP/IP协议模型)各种io模型的知识http协议和tcp协议的区别https和http的区别…...
)
Android14音频进阶之<进阶调试>:Perfetto定位系统音频问题(六十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒体系统工程师系列【原创干货持续更新中……】🚀 优质视频课程:AAOS车载系统+AOSP…...
使用 Clickhouse 集成的表引擎同步数据方式详解
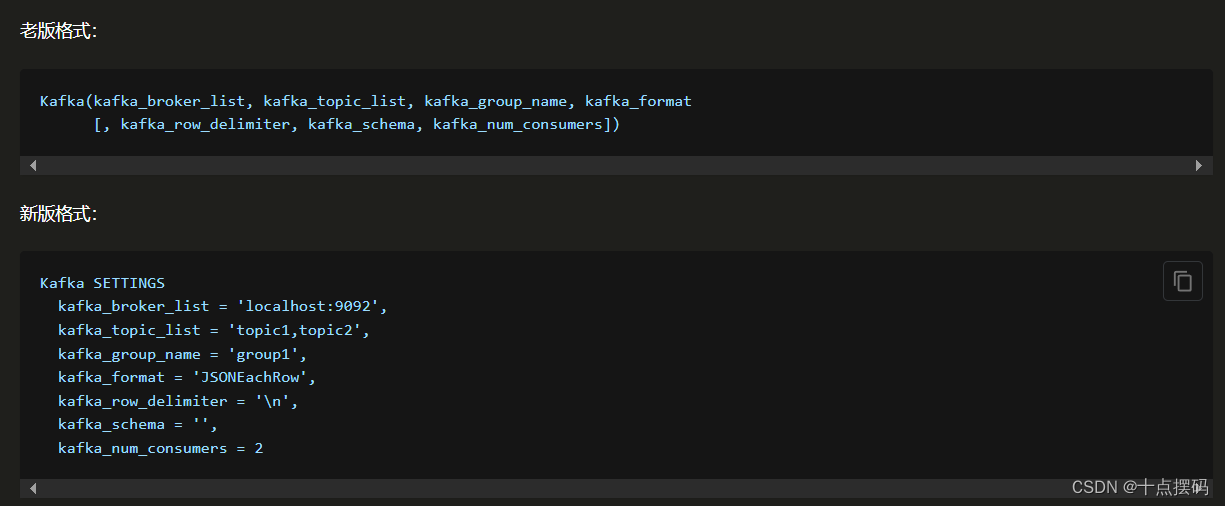
Clickhouse作为一个列式存储分析型数据库,提供了很多集成其他组件的表引擎数据同步方案。 官网介绍 一 Kafka 表引擎 使用Clickhouse集成的Kafka表引擎消费Kafka写入Clickhouse表中。 1.1 流程图 1.2 建表 根据上面的流程图需要建立三张表,分别Click…...
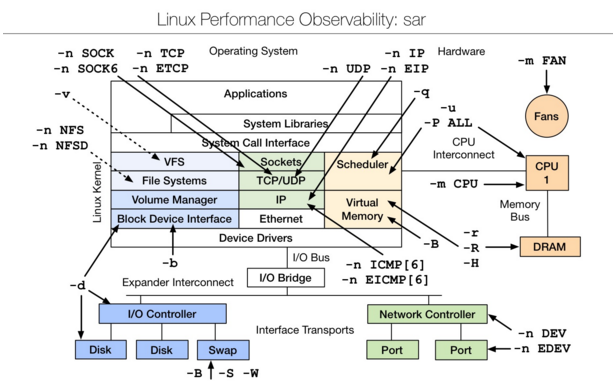
Linux 性能分析工具大全
vmstat--虚拟内存统计 vmstat(VirtualMeomoryStatistics,虚拟内存统计)是 Linux 中监控内存的常用工具,可对操作系统的虚拟内存、进程、CPU 等的整体情况进行监视。vmstat 的常规用法:vmstat interval times 即每隔 interval 秒采…...

FME学习之旅---day21
我们付出一些成本,时间的或者其他,最终总能收获一些什么。 教程:AutoCAD 变换 相关的文章 为您的 DWG 赋予一些样式:使用 DWGStyler、模板文件、块等 FME数据检查器在显示行的方式上受到限制。它只能显示线条颜色,而…...
volta(轻松切换管理Node.js版本)
Node.js版本管理 Volta提供了一个简单直观的命令行界面,可以轻松地安装、卸载、更新和切换Node.js版本。 Volta 既可以全局使用,也可以在项目级别使用,可以为每个项目单独设置node版本,nvm不行。 下载安装Volta 参考: …...

机器学习知识点
1鸢尾花分类 鸢尾花分类问题是一个经典的机器学习问题,旨在根据鸢尾花的花萼长度、花萼宽度、花瓣长度和花瓣宽度等特征,将鸢尾花分成三个品种:山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚…...

SQL注入利用学习-Union联合注入
联合注入的原理 在SQL语句中查询数据时,使用select 相关语句与where 条件子句筛选符合条件的记录。 select * from person where id 1; #在person表中,筛选出id1的记录如果该id1 中的1 是用户可以控制输入的部分时,就有可能存在SQL注入漏洞…...

zookeeper源码(12)命令行客户端
zkCli.sh脚本 这个命令行脚本在bin目录下: ZOOBIN"${BASH_SOURCE-$0}" ZOOBIN"$(dirname "${ZOOBIN}")" ZOOBINDIR"$(cd "${ZOOBIN}"; pwd)"# 加载zkEnv.sh脚本 if [ -e "$ZOOBIN/../libexec/zkEnv.sh&qu…...

深度学习的数学基础--Homework2
学习资料:https://www.bilibili.com/video/BV1mg4y187qv/?spm_id_from333.788.recommend_more_video.1&vd_sourced6b1de7f052664abab680fc242ef9bc1 神经网络的特点:它不是一个解析模型,它的储存在一堆参数里面(确定一个超平…...

什么是HW,企业如何进行HW保障?
文章目录 一、什么是HW二、HW行动具体采取了哪些攻防演练措施三、攻击方一般的攻击流程和方法四、企业HW保障方案1.建意识2.摸家底3.固城池4.配神器5.增值守 一、什么是HW 网络安全形势近年出现新变化,网络安全态势变得越来越复杂,黑客攻击入侵、勒索病…...

【Redis系列】Spring Boot 集成 Redis 实现缓存功能
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
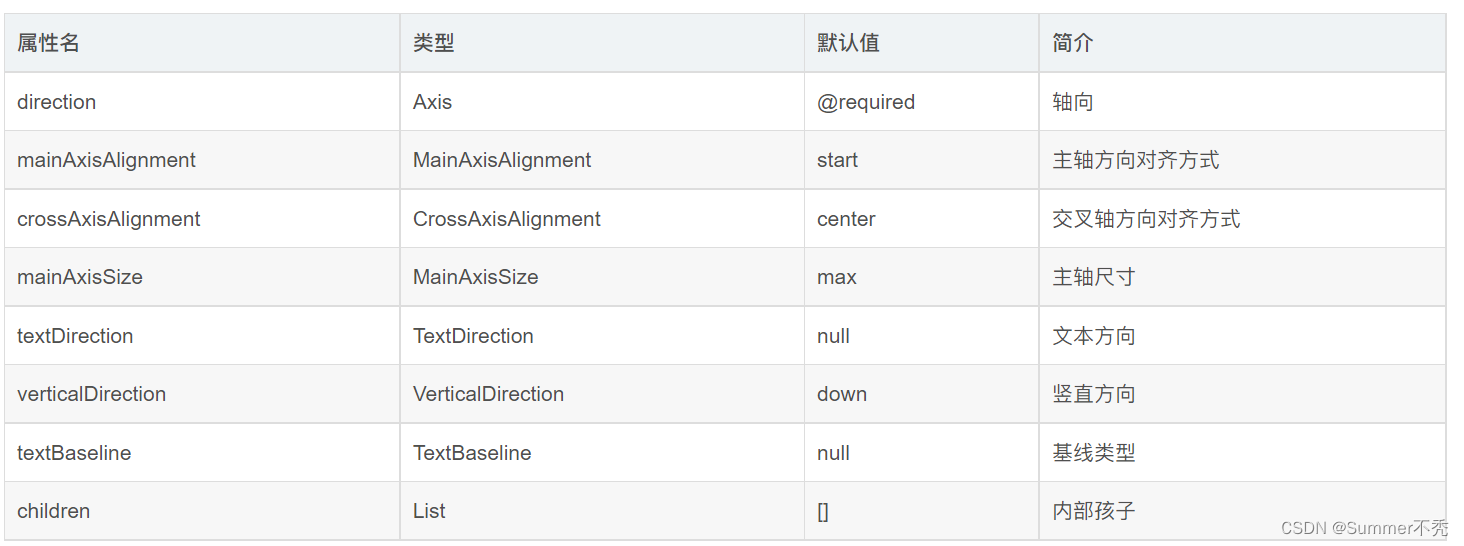
Flutter之Flex组件布局
目录 Flex属性值 轴向:direction:Axis.horizontal 主轴方向:mainAxisAlignment:MainAxisAlignment.center 交叉轴方向:crossAxisAlignment:CrossAxisAlignment 主轴尺寸:mainAxisSize 文字方向:textDirection:TextDirection 竖直方向排序:verticalDirection:VerticalDir…...
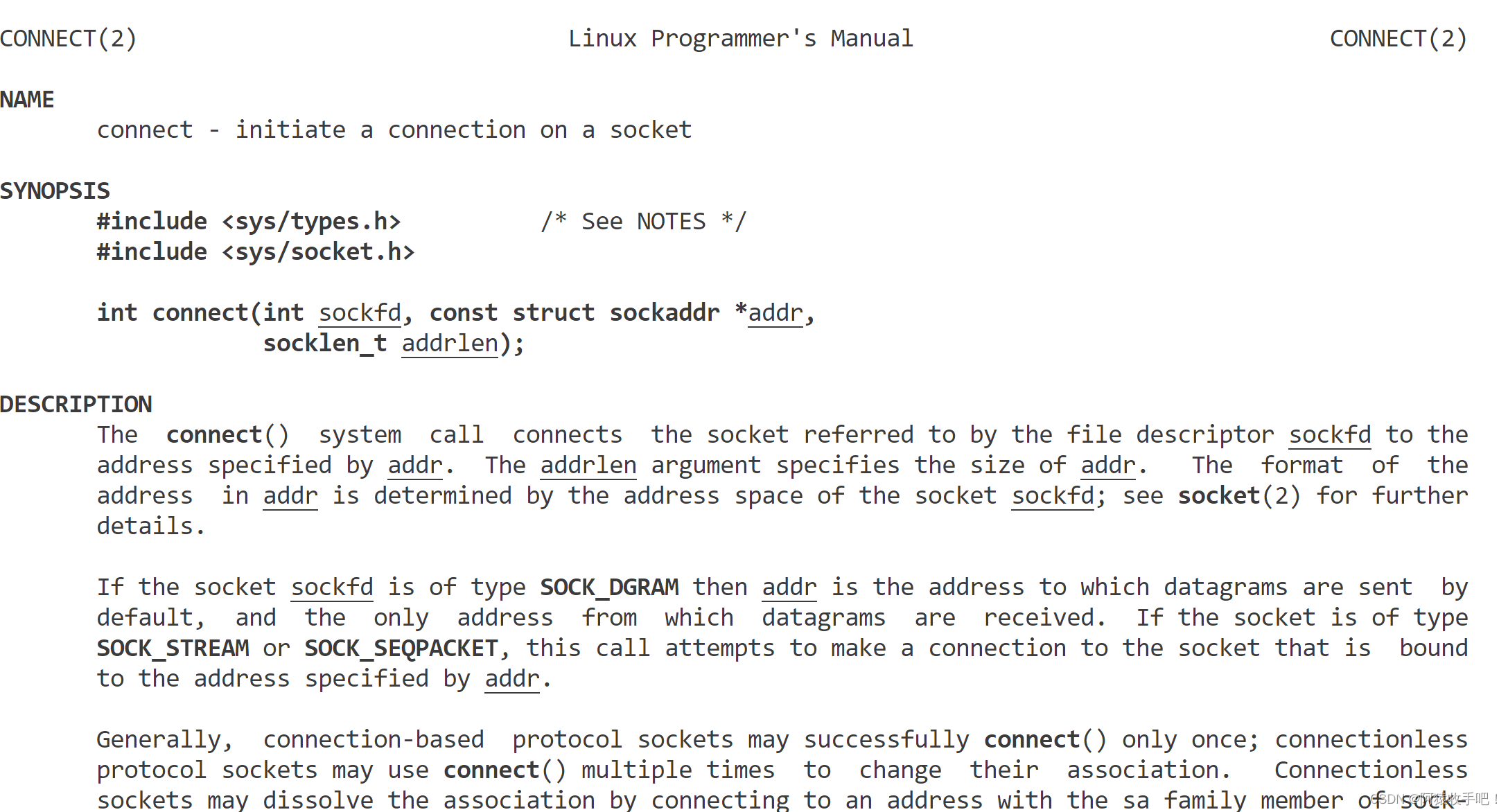
【Linux】TCP编程{socket/listen/accept/telnet/connect/send}
文章目录 1.TCP接口1.1socket文档 1.2listen拓:端口号8080 1.3accept拓:今天全局函数 1.4读写接口1.5telnet1.一个客户端2.两个客户端 1.6ulimit -a1.7常识回顾1.8connect1.9拓:客户端的ip和地址什么时候被分配?1.10拓:…...

【WPF应用33】WPF基本控件-TabControl的详解与示例
在Windows Presentation Foundation(WPF)中,TabControl控件是一个强大的界面元素,它允许用户在多个标签页之间切换,每个标签页都可以显示不同的内容。这种控件在组织信息、提供选项卡式界面等方面非常有用。在本篇博客…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
