深度学习的数学基础--Homework2
学习资料:https://www.bilibili.com/video/BV1mg4y187qv/?spm_id_from=333.788.recommend_more_video.1&vd_source=d6b1de7f052664abab680fc242ef9bc1
神经网络的特点:它不是一个解析模型,它的储存在一堆参数里面(确定一个超平面),很难解释物理意义是什么,不能直观看出来。
评价网络的好坏:主要看的不是它的精度,而是看它是否具有很好的泛化能力(测试集)。
1943 M-P模型的3种形式(文字、公式、图形描述神经元)->1958 单层感知器->1986 误差反向传播(解决隐层权重求解)作为多层感知器的算法
Note:
1.数学模型是抽象出来的,所以把不方便考虑到可以简化掉
2.加权求和–实际上是对神经元接收到的信号进行空间整合(为什么没有时间整合,因为模型假设认为信号同时到达的)
3.为什么要有阈值:并不是膜电位改变后一定有输出,有输出的一定是膜电位改变超过了阈值,超过阈值以后才产生一个输出,这个【输出】和【改变后超出阈值的膜电位变化值】之间是一个函数关系,f是输出函数/转移函数/激活函数 ,x(t)是输入信号
4.多层感知器(又称三层BP网),因为大部分多层感知器的算法是BP算法,但实际上还有其它算法。此处三层包括了输入层,实际上具有信号处理能力的层只有两层。
5.误差信号 δ j y \delta_{j}^{y} δjy, δ k o \delta_{k}^{o} δko≠误差 Δ v \Delta{v} Δv, Δ w \Delta{w} Δw。为什么引入误差信号的概念呢?从网络前向传播角度看,可以方便表示权值修正公式;从网络反向传播角度看,将误差信号作为输入层可以计算隐藏层的误差。
误差信号的构成有三个部分。
6.为什么要进行误差反传:由于只有输出层有教师信号(监督信号),输出层误差可以计算,而中间层并没有教师信号,所以这导致隐藏层的误差无法计算,因此也无法得到权值调整公式 Δ v \Delta{v} Δv。
为了能够调整初始化的权值参数/让婴儿的大脑习得知识,我们用输出层的误差信号反传(反传过程中,误差信号相当于一个输入向量,需要对输入向量加权求和),从而得到隐藏层的误差信号。一旦隐藏层的误差信号有了,就可以算出来权值调整公式即隐藏层的误差。简言之,为了反传时可以根据误差信号获得隐藏层的误差)

单层感知器的功能:线性分类器分类的原理:把分类的知识分布式地存储在权向量(参数)里面
调参:就是调整分类界面的位置
相关文章:

深度学习的数学基础--Homework2
学习资料:https://www.bilibili.com/video/BV1mg4y187qv/?spm_id_from333.788.recommend_more_video.1&vd_sourced6b1de7f052664abab680fc242ef9bc1 神经网络的特点:它不是一个解析模型,它的储存在一堆参数里面(确定一个超平…...

什么是HW,企业如何进行HW保障?
文章目录 一、什么是HW二、HW行动具体采取了哪些攻防演练措施三、攻击方一般的攻击流程和方法四、企业HW保障方案1.建意识2.摸家底3.固城池4.配神器5.增值守 一、什么是HW 网络安全形势近年出现新变化,网络安全态势变得越来越复杂,黑客攻击入侵、勒索病…...

【Redis系列】Spring Boot 集成 Redis 实现缓存功能
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
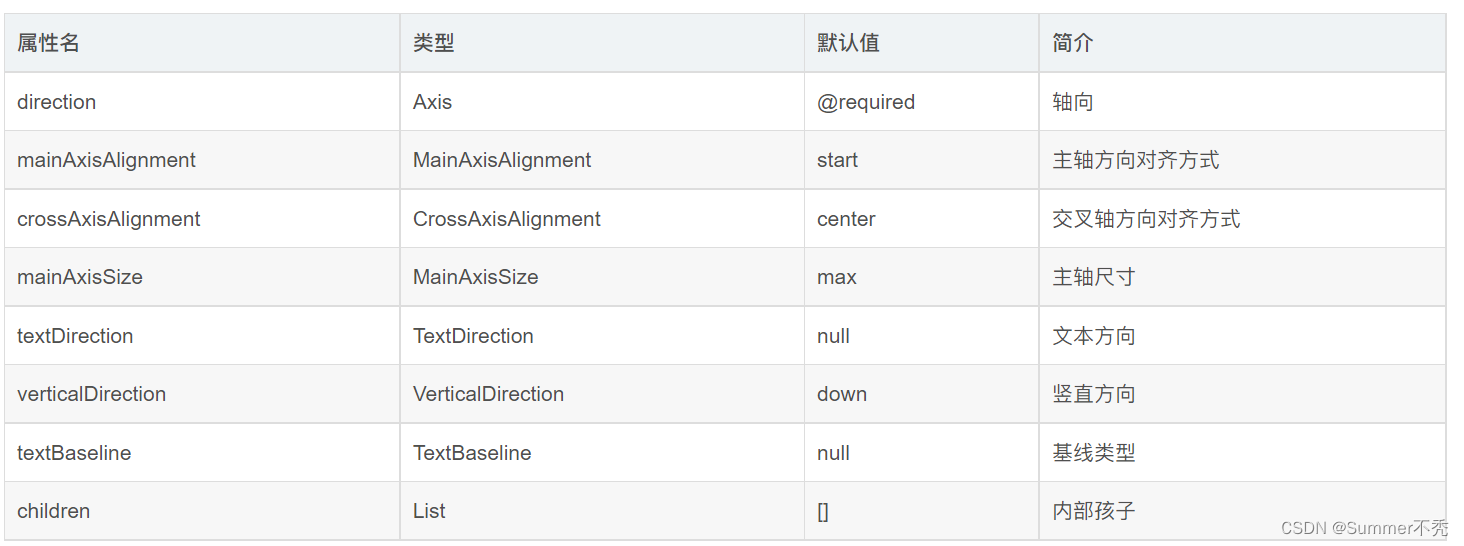
Flutter之Flex组件布局
目录 Flex属性值 轴向:direction:Axis.horizontal 主轴方向:mainAxisAlignment:MainAxisAlignment.center 交叉轴方向:crossAxisAlignment:CrossAxisAlignment 主轴尺寸:mainAxisSize 文字方向:textDirection:TextDirection 竖直方向排序:verticalDirection:VerticalDir…...
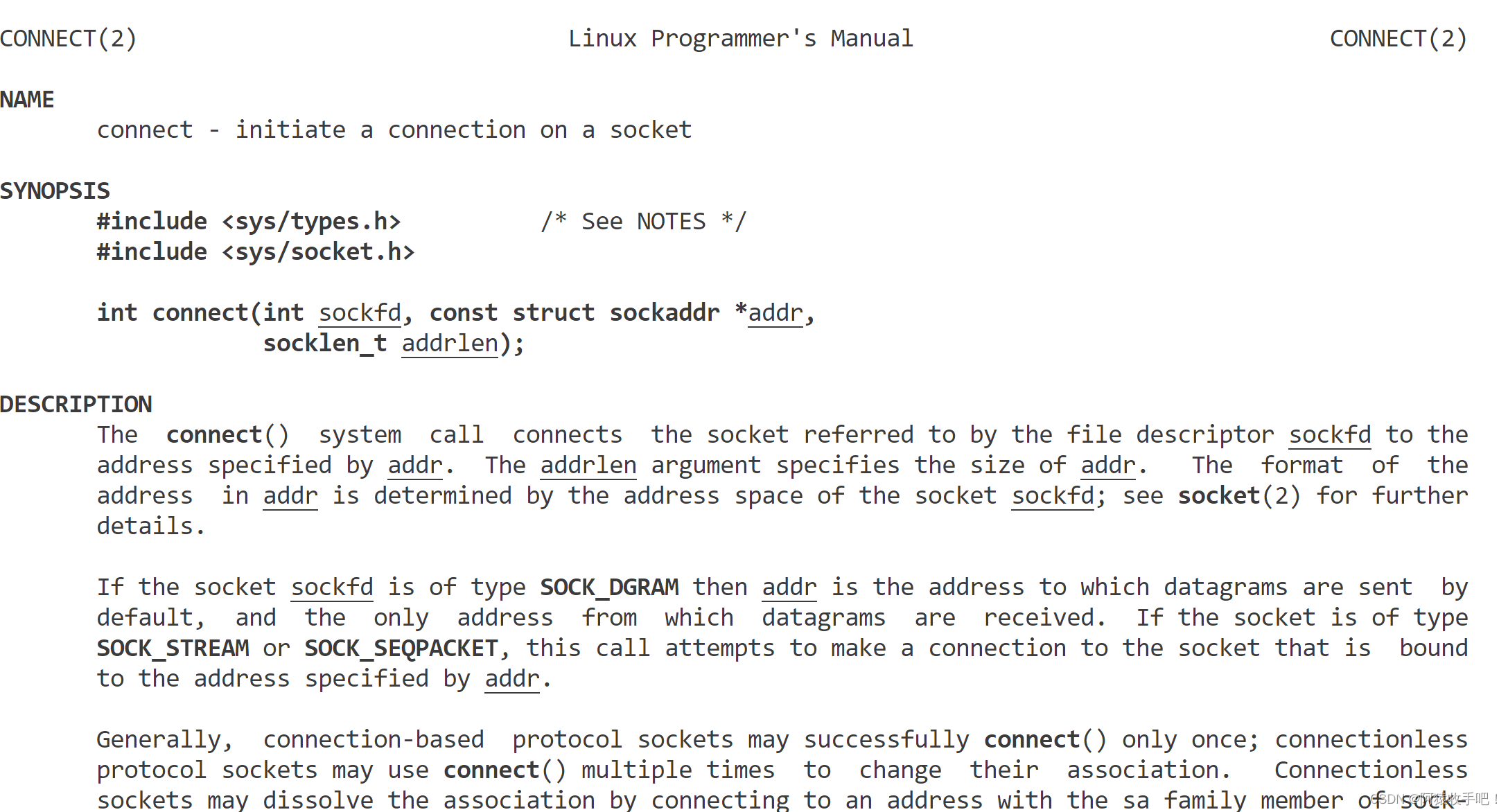
【Linux】TCP编程{socket/listen/accept/telnet/connect/send}
文章目录 1.TCP接口1.1socket文档 1.2listen拓:端口号8080 1.3accept拓:今天全局函数 1.4读写接口1.5telnet1.一个客户端2.两个客户端 1.6ulimit -a1.7常识回顾1.8connect1.9拓:客户端的ip和地址什么时候被分配?1.10拓:…...

【WPF应用33】WPF基本控件-TabControl的详解与示例
在Windows Presentation Foundation(WPF)中,TabControl控件是一个强大的界面元素,它允许用户在多个标签页之间切换,每个标签页都可以显示不同的内容。这种控件在组织信息、提供选项卡式界面等方面非常有用。在本篇博客…...

[C语言]——动态内存管理
目录 一.为什么要有动态内存分配 二.malloc和free 1.malloc 2.free 三.calloc和realloc 1.calloc 2.realloc 3.空间的释放编辑 四.常见的动态内存的错误 1.对NULL指针的解引用操作 2.对动态开辟空间的越界访问 3.对非动态开辟内存使用free释放 4.使用free释放⼀块…...
C++ 学习笔记
文章目录 【 字符串相关 】C 输入输出流strcpy_s() 字符串复制输出乱码 【 STL 】各个 STL 支持的常见方法 ? : 运算符switch case 运算符 switch(expression) {case constant-expression :statement(s);break; // 可选的case constant-expression :statement(s);break; //…...

本科生学深度学习一残差网络,解决梯度消失和爆炸
看到订阅的激励还在继续,今天写下残差网络 1、梯度爆炸和梯度消失 梯度爆炸和梯度消失是两种常见的问题,由神经网络的结构和参数初始化方式引起。它们都与深度神经网络中的反向传播过程相关。 梯度爆炸:这是指在反向传播期间,梯度逐渐增大并最终超出了有效范围。这通常发…...

初识SpringMVC
一、什么是MVC MVC是一种软件架构模式(是一种软件架构设计思想,不止Java开发中用到,其它语言也需要用到),它将应用分为三块: M:Model(模型)V:View(…...

【Leetcode】2009. 使数组连续的最少操作数
文章目录 题目思路代码复杂度分析时间复杂度空间复杂度 结果总结 题目 题目链接🔗 给你一个整数数组 n u m s nums nums 。每一次操作中,你可以将 n u m s nums nums 中 任意 一个元素替换成 任意 整数。 如果 n u m s nums nums 满足以下条件&…...

LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】
LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】 题目描述:解题思路一:哈希表记录出现次数,然后用最小堆取,因为每次都是弹出最小的,剩下的一定是K…...

K8S Deployment HA
文章目录 K8S Deployment HA1.机器规划2.前期准备2.1 安装ansible2.2 修改 hostname2.3 配置免密2.4 时间同步2.5 系统参数调整2.6 安装 Docker2.7 部署 HaproxyKeepalived 3. 部署 K8S3.1 安装 k8s命令3.2 k8s初始化3.3 添加其他master节点3.4 添加 Node节点3.5 安装 CNI3.6 查…...

【Linux】linux 在指定根目录下,查找wav文件并删除
要在Linux的指定根目录下查找.wav文件并删除它们,您可以使用find命令结合-exec选项来执行删除操作。请注意,这个操作是不可逆的,所以在执行之前请确保您知道自己在做什么,并且已经备份了重要数据。 以下是一个示例命令࿰…...
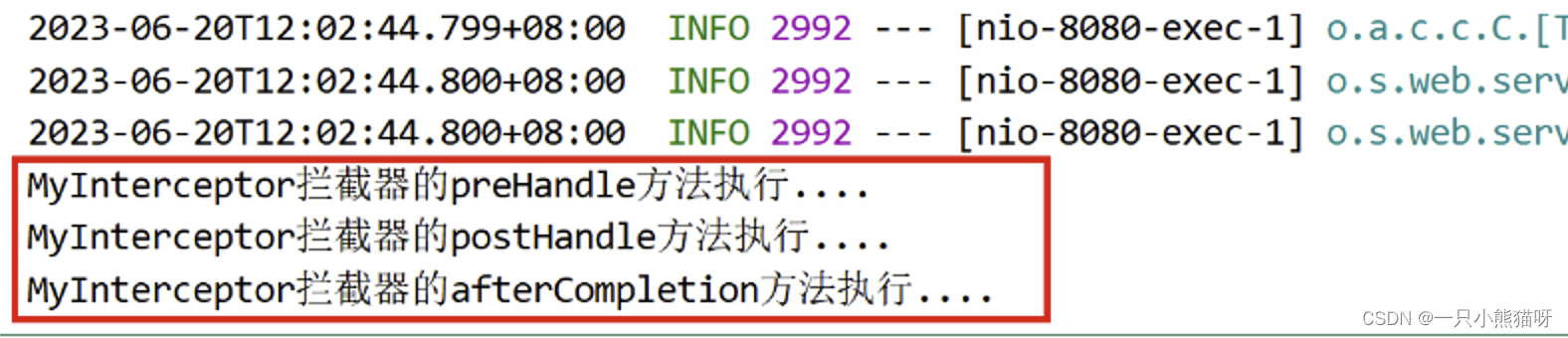
三、SpringBoot3 整合 SpringMVC
本章概要 实现过程web 相关配置静态资源处理自定义拦截器(SpringMVC 配置) 3.1 实现过程 创建程序引入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www…...
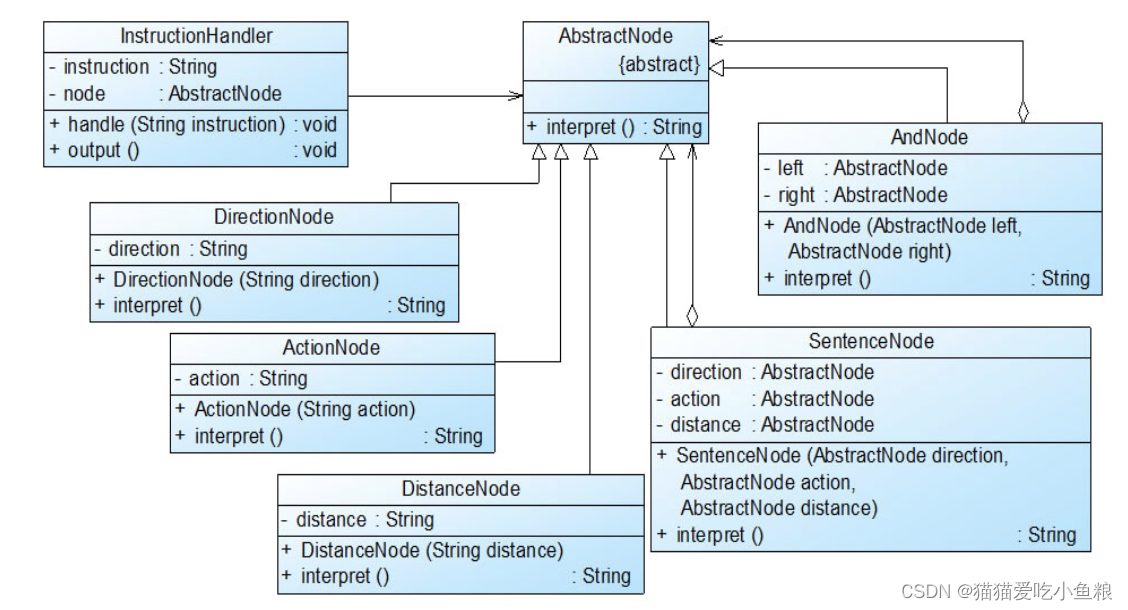
设计模式之解释器模式(上)
解释器模式 1)概述 1.定义 定义一个语言的文法,并且建立一个解释器来解释该语言中的句子,这里的“语言”是指使用规定格式和语法的代码。 2.结构图 3.角色 AbstractExpression(抽象表达式):在抽象表达…...

[23年蓝桥杯] 买二赠一
题目描述 【问题描述】 某商场有 N 件商品,其中第 i 件的价格是 A i 。现在该商场正在进行 “ 买二 赠一” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P (如果两件商品价格一样, 则…...

PgSQL的with as语法
returning 返回的这一些字段,然后进行汇总为remove_alarms 然后select一下remove_alarms 出来的数据然后保存到tb_alarm_his 里面 with remove_alarms as( delete fromtb_alarm whereid in (508) returning 0,now(),admin,alarmadvice,alarmadvicecn,alarmarises…...

六、c++代码中的安全风险-fopen
(misc) fopen: Check when opening files - can an attacker redirect it (via symlinks), force the opening of special file type (e.g., device files), move things around to create a race condition, control its ancestors, or change its contents? (CWE-362). 为…...
uniapp项目问题及解决(前后端互联)
1.路由跳转的问题 uni.navigateTo() 保留当前页面,跳转到应用内的某个页面,使用uni.navigateBack可以返回到原页面 uni.redirectTo() 关闭当前页面,跳转到应用内的某个页面。 uni.reLaunch&…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
