【Leetcode】2009. 使数组连续的最少操作数
文章目录
- 题目
- 思路
- 代码
- 复杂度分析
- 时间复杂度
- 空间复杂度
- 结果
- 总结
题目
题目链接🔗
给你一个整数数组 n u m s nums nums 。每一次操作中,你可以将 n u m s nums nums 中 任意 一个元素替换成 任意 整数。
如果 n u m s nums nums 满足以下条件,那么它是 连续的 :
n u m s nums nums 中所有元素都是 互不相同 的。
n u m s nums nums 中 最大 元素与 最小 元素的差等于 n u m s . l e n g t h − 1 nums.length - 1 nums.length−1 。
比方说, n u m s = [ 4 , 2 , 5 , 3 ] nums = [4, 2, 5, 3] nums=[4,2,5,3] 是 连续的 ,但是 n u m s = [ 1 , 2 , 3 , 5 , 6 ] nums = [1, 2, 3, 5, 6] nums=[1,2,3,5,6] 不是连续的 。
请你返回使 nums 连续 的 最少 操作次数。
示例 1:
输入:nums = [4,2,5,3]
输出:0
解释:nums 已经是连续的了。
示例 2:
输入:nums = [1,2,3,5,6]
输出:1
解释:一个可能的解是将最后一个元素变为 4 。
结果数组为 [1,2,3,5,4] ,是连续数组。
示例 3:
输入:nums = [1,10,100,1000]
输出:3
解释:一个可能的解是:
- 将第二个元素变为 2 。
- 将第三个元素变为 3 。
- 将第四个元素变为 4 。
结果数组为 [1,2,3,4] ,是连续数组。
提示:
- 1 ≤ n u m s . l e n g t h ≤ 1 0 5 1 \leq nums.length \leq 10^5 1≤nums.length≤105
- 1 ≤ n u m s [ i ] ≤ 1 0 9 1 \leq nums[i] \leq 10^9 1≤nums[i]≤109
思路
- 对数组进行排序,这样相邻的元素就可以保证是连续的。然后去除重复元素,确保数组中的元素互不相同。对于数组中的每个元素 n u m s [ i ] nums[i] nums[i],我们需要找到满足条件的最大元素 n u m s [ j ] nums[j] nums[j],使得 n u m s [ j ] − n u m s [ i ] = n u m s . s i z e ( ) − 1 nums[j] - nums[i] = nums.size() - 1 nums[j]−nums[i]=nums.size()−1。
- 使用二分查找来寻找满足条件的最大元素。具体地,可以遍历数组中的每个元素 n u m s [ i ] nums[i] nums[i],然后使用二分查找找到最大值不超过 n u m s [ i ] + n u m s . s i z e ( ) − 1 nums[i] + nums.size() - 1 nums[i]+nums.size()−1 的元素,即 n u m s [ j ] ≤ n u m s [ i ] + n u m s . s i z e ( ) − 1 nums[j] \leq nums[i] + nums.size() - 1 nums[j]≤nums[i]+nums.size()−1。
- 对于每个元素 n u m s [ i ] nums[i] nums[i],可以计算需要的操作次数为 n u m s . s i z e ( ) − ( j − i + 1 ) nums.size() - (j - i + 1) nums.size()−(j−i+1),其中 j j j 是满足条件的最大元素的下标。
代码
class Solution {
public:int minOperations(vector<int>& nums) {ranges::sort(nums);int n = nums.size();nums.resize(unique(nums.begin(), nums.end()) - nums.begin());int m = nums.size();int res = INT_MAX;for(int i = 0; i < m; i++) {int x = nums[i];int y = x + n - 1;int l = i, r = m - 1;while(l < r) {int mid = (l + r + 1) / 2;if(nums[mid] > y) r = mid - 1;else l = mid;}res = min(res, n - (l - i + 1));} return res;}
};
复杂度分析
时间复杂度
O ( n log n ) O(n \log n) O(nlogn)
空间复杂度
O ( 1 ) O(1) O(1)
结果

总结
关键在于如何通过排序和遍历找到满足条件的最小操作次数。我们通过排序数组并去除重复元素,然后对每个元素进行遍历,通过二分查找找到最大值不超过 y y y 的元素,并计算需要的操作次数,最后选择操作次数最小的那个作为结果。
相关文章:

【Leetcode】2009. 使数组连续的最少操作数
文章目录 题目思路代码复杂度分析时间复杂度空间复杂度 结果总结 题目 题目链接🔗 给你一个整数数组 n u m s nums nums 。每一次操作中,你可以将 n u m s nums nums 中 任意 一个元素替换成 任意 整数。 如果 n u m s nums nums 满足以下条件&…...

LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】
LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】 题目描述:解题思路一:哈希表记录出现次数,然后用最小堆取,因为每次都是弹出最小的,剩下的一定是K…...

K8S Deployment HA
文章目录 K8S Deployment HA1.机器规划2.前期准备2.1 安装ansible2.2 修改 hostname2.3 配置免密2.4 时间同步2.5 系统参数调整2.6 安装 Docker2.7 部署 HaproxyKeepalived 3. 部署 K8S3.1 安装 k8s命令3.2 k8s初始化3.3 添加其他master节点3.4 添加 Node节点3.5 安装 CNI3.6 查…...

【Linux】linux 在指定根目录下,查找wav文件并删除
要在Linux的指定根目录下查找.wav文件并删除它们,您可以使用find命令结合-exec选项来执行删除操作。请注意,这个操作是不可逆的,所以在执行之前请确保您知道自己在做什么,并且已经备份了重要数据。 以下是一个示例命令࿰…...
三、SpringBoot3 整合 SpringMVC
本章概要 实现过程web 相关配置静态资源处理自定义拦截器(SpringMVC 配置) 3.1 实现过程 创建程序引入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www…...
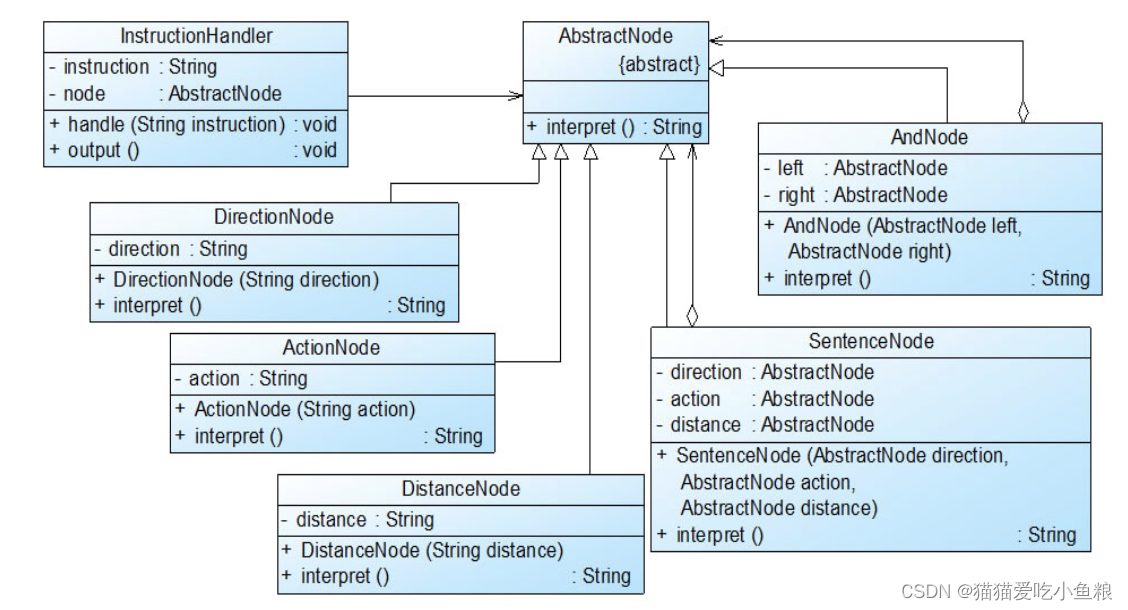
设计模式之解释器模式(上)
解释器模式 1)概述 1.定义 定义一个语言的文法,并且建立一个解释器来解释该语言中的句子,这里的“语言”是指使用规定格式和语法的代码。 2.结构图 3.角色 AbstractExpression(抽象表达式):在抽象表达…...

[23年蓝桥杯] 买二赠一
题目描述 【问题描述】 某商场有 N 件商品,其中第 i 件的价格是 A i 。现在该商场正在进行 “ 买二 赠一” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P (如果两件商品价格一样, 则…...

PgSQL的with as语法
returning 返回的这一些字段,然后进行汇总为remove_alarms 然后select一下remove_alarms 出来的数据然后保存到tb_alarm_his 里面 with remove_alarms as( delete fromtb_alarm whereid in (508) returning 0,now(),admin,alarmadvice,alarmadvicecn,alarmarises…...

六、c++代码中的安全风险-fopen
(misc) fopen: Check when opening files - can an attacker redirect it (via symlinks), force the opening of special file type (e.g., device files), move things around to create a race condition, control its ancestors, or change its contents? (CWE-362). 为…...
uniapp项目问题及解决(前后端互联)
1.路由跳转的问题 uni.navigateTo() 保留当前页面,跳转到应用内的某个页面,使用uni.navigateBack可以返回到原页面 uni.redirectTo() 关闭当前页面,跳转到应用内的某个页面。 uni.reLaunch&…...
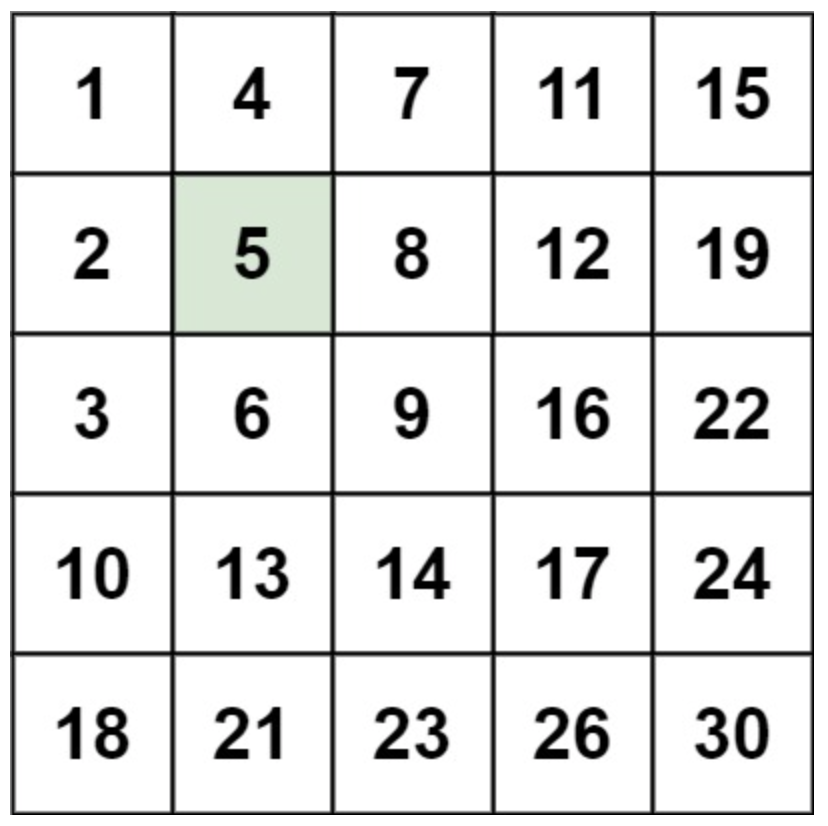
面试算法-154-搜索二维矩阵 II
题目 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。 每列的元素从上到下升序排列。 示例 1: 输入:matrix [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,…...

Java中Stream流介绍
Java 8引入的Stream API是Java中处理集合的一种高效方式,它提供了一种高级的迭代方式,允许你以声明式方式处理数据。Stream API可以对数据执行复杂的查询操作,而不需要编写冗长且复杂的循环语句。下面是一些使用Stream API的常见场景和示例&a…...

深度学习的层、算子和函数空间
目录 一、层、算子和函数空间概念 二、层(Layers) 三、算子(Operators) 3.1常见算子 3.2常见算子的性质 四、函数空间(Function Space) 一、层、算子和函数空间概念 层(Layers)…...

Pillow教程11:九宫格切图的实现方法(安排!!!)
---------------Pillow教程集合--------------- Python项目18:使用Pillow模块,随机生成4位数的图片验证码 Python教程93:初识Pillow模块(创建Image对象查看属性图片的保存与缩放) Pillow教程02:图片的裁…...

Macos 部署自己的privateGpt(2024-0404)
Private Chatgpt 安装指引 https://docs.privategpt.dev/installation/getting-started/installation#base-requirements-to-run-privategpt 下载源码 git clone https://github.com/imartinez/privateGPT cd privateGPT安装软件 安装: Homebrew /bin/bash -c…...

先安装CUDA后安装Visual Studio的额外配置
VS新建项目中增加CUDA选项 以vs2019 cuda 11.3为例 关闭vs2019解压cuda的windows安装包cuda_11.3.0_465.89_win10.exe进入路径cuda_11.3.0_465.89_win10\visual_studio_integration\CUDAVisualStudioIntegration\extras\visual_studio_integration\CudaProjectVsWizards\拷贝…...

2024 蓝桥打卡Day35
20240407蓝桥杯备赛 1、学习蓝桥云课省赛冲刺课 【3-搜索算法】【4-枚举与尺度法】2、学习蓝桥云课Java省赛无忧班 【1-语言基础】3、代码练习数字反转数字反转优化算法sort排序相关String字符串相关StringBuilder字符串相关HashSet相关 1、学习蓝桥云课省赛冲刺课 【3-搜索算法…...
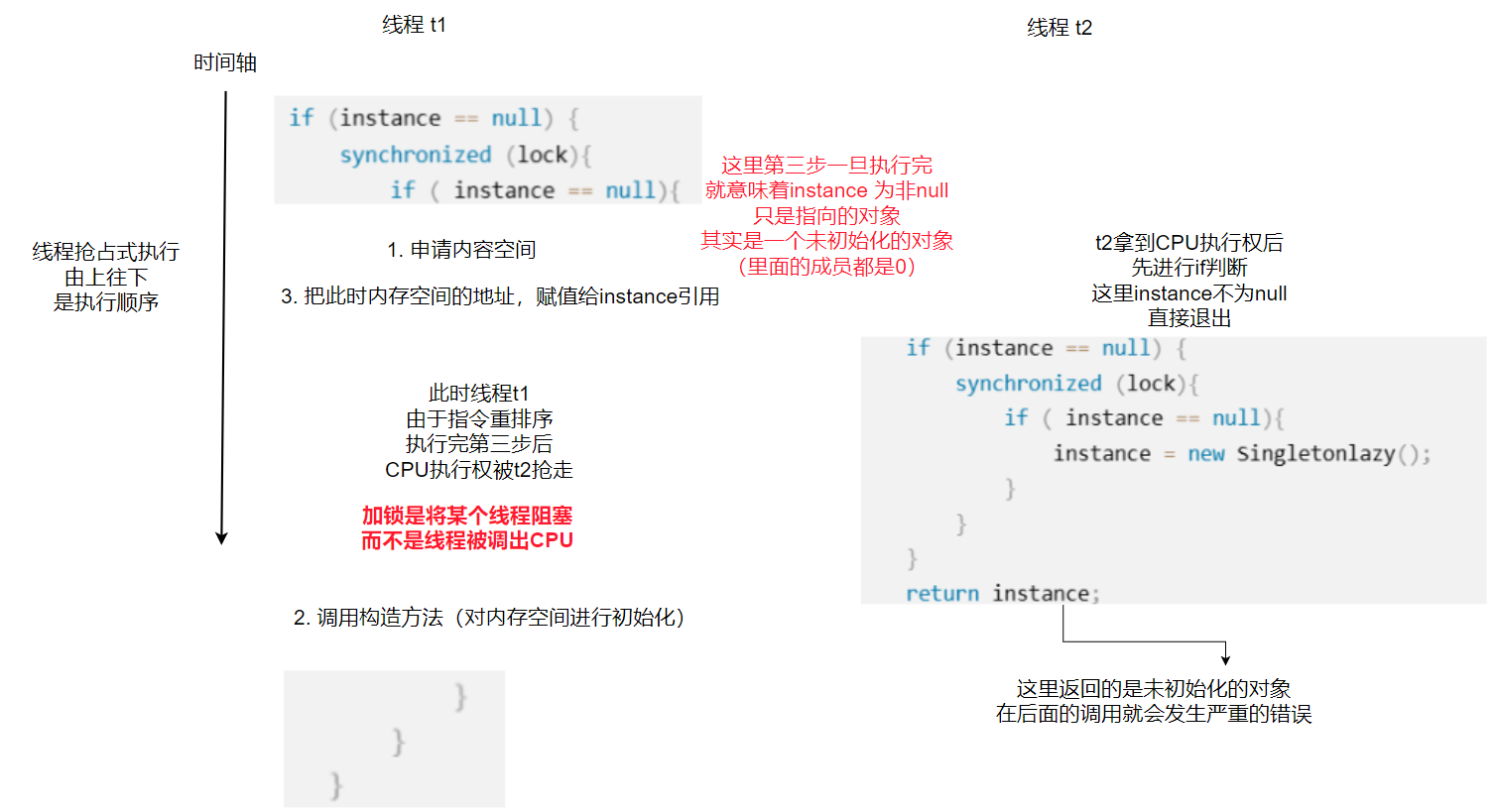
【Java】单例模式
单例模式是面试中常考的设计模式之一 在面试中,面试官常常会要求写出两种类型的单例模式并解释原理 本文中,将从0到1的介绍单例模式究竟是什么 文章目录 ✍一、什么是设计模式?✍二、单例模式是什么?✍三、单例模式的类型**1.饿汉…...

Linux|从 STDIN 读取 Awk 输入
简介 在之前关于 Awk 工具的系列文章中,主要探讨了如何从文件中读取数据。但如果你希望从标准输入(STDIN)中读取数据,又该如何操作呢? 在本文中,将介绍几个示例,展示如何使用 Awk 来过滤其他命令…...

关于K8S集群中maste节点r和worker节点的20道面试题
1. 什么是Kubernetes(K8S)? Kubernetes(通常简称为K8S)是一种开源的容器编排平台,用于自动化部署、扩展和管理容器化应用程序。以下是Kubernetes的一些核心特性和优势: 自动化部署和扩展&…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
