LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】
LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】
- 题目描述:
- 解题思路一:哈希表记录出现次数,然后用最小堆取,因为每次都是弹出最小的,剩下的一定是K个最大的。
- 解题思路二:直接排序
- 解题思路三:堆
- 解题思路三:快速排序
题目描述:
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
1 <= nums.length <= 105
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的
进阶:你所设计算法的时间复杂度 必须 优于 O(n log n) ,其中 n 是数组大小。
解题思路一:哈希表记录出现次数,然后用最小堆取,因为每次都是弹出最小的,剩下的一定是K个最大的。
import heapq # 默认是最小堆
class Solution:def topKFrequent(self, nums: List[int], k: int) -> List[int]:map_ = {}for i in range(len(nums)):map_[nums[i]] = map_.get(nums[i], 0) + 1pri_que = []for key, freq in map_.items():heapq.heappush(pri_que, (freq, key))if len(pri_que) > k: heapq.heappop(pri_que)result = [0] * kfor i in range(k-1, -1, -1):result[i] = heapq.heappop(pri_que)[1]return result
时间复杂度:O(nlogk)
空间复杂度:O(n)
解题思路二:直接排序
class Solution:def topKFrequent(self, nums: List[int], k: int) -> List[int]:count = collections.Counter(nums)return [item[0] for item in count.most_common(k)]
时间复杂度:O(nlogn)
空间复杂度:O(n)
解题思路三:堆
class Solution:def topKFrequent(self, nums: List[int], k: int) -> List[int]:count = collections.Counter(nums)heap = [(val, key) for key, val in count.items()]return [item[1] for item in heapq.nlargest(k, heap)]
时间复杂度:O(nlogn)
空间复杂度:O(n)
解题思路三:快速排序

class Solution:def topKFrequent(self, nums: List[int], k: int) -> List[int]:count = collections.Counter(nums)num_cnt = list(count.items())topKs = self.findTopK(num_cnt, k, 0, len(num_cnt) - 1)return [item[0] for item in topKs]def findTopK(self, num_cnt, k, low, high):pivot = random.randint(low, high)num_cnt[low], num_cnt[pivot] = num_cnt[pivot], num_cnt[low]base = num_cnt[low][1]i = lowfor j in range(low + 1, high + 1):if num_cnt[j][1] > base:num_cnt[i + 1], num_cnt[j] = num_cnt[j], num_cnt[i + 1]i += 1num_cnt[low], num_cnt[i] = num_cnt[i], num_cnt[low]if i == k - 1:return num_cnt[:k]elif i > k - 1:return self.findTopK(num_cnt, k, low, i - 1)else:return self.findTopK(num_cnt, k, i + 1, high)
时间复杂度:O(n)
空间复杂度:O(n)
相关文章:

LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】
LeetCode-347. 前 K 个高频元素【数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)】 题目描述:解题思路一:哈希表记录出现次数,然后用最小堆取,因为每次都是弹出最小的,剩下的一定是K…...

K8S Deployment HA
文章目录 K8S Deployment HA1.机器规划2.前期准备2.1 安装ansible2.2 修改 hostname2.3 配置免密2.4 时间同步2.5 系统参数调整2.6 安装 Docker2.7 部署 HaproxyKeepalived 3. 部署 K8S3.1 安装 k8s命令3.2 k8s初始化3.3 添加其他master节点3.4 添加 Node节点3.5 安装 CNI3.6 查…...

【Linux】linux 在指定根目录下,查找wav文件并删除
要在Linux的指定根目录下查找.wav文件并删除它们,您可以使用find命令结合-exec选项来执行删除操作。请注意,这个操作是不可逆的,所以在执行之前请确保您知道自己在做什么,并且已经备份了重要数据。 以下是一个示例命令࿰…...
三、SpringBoot3 整合 SpringMVC
本章概要 实现过程web 相关配置静态资源处理自定义拦截器(SpringMVC 配置) 3.1 实现过程 创建程序引入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www…...
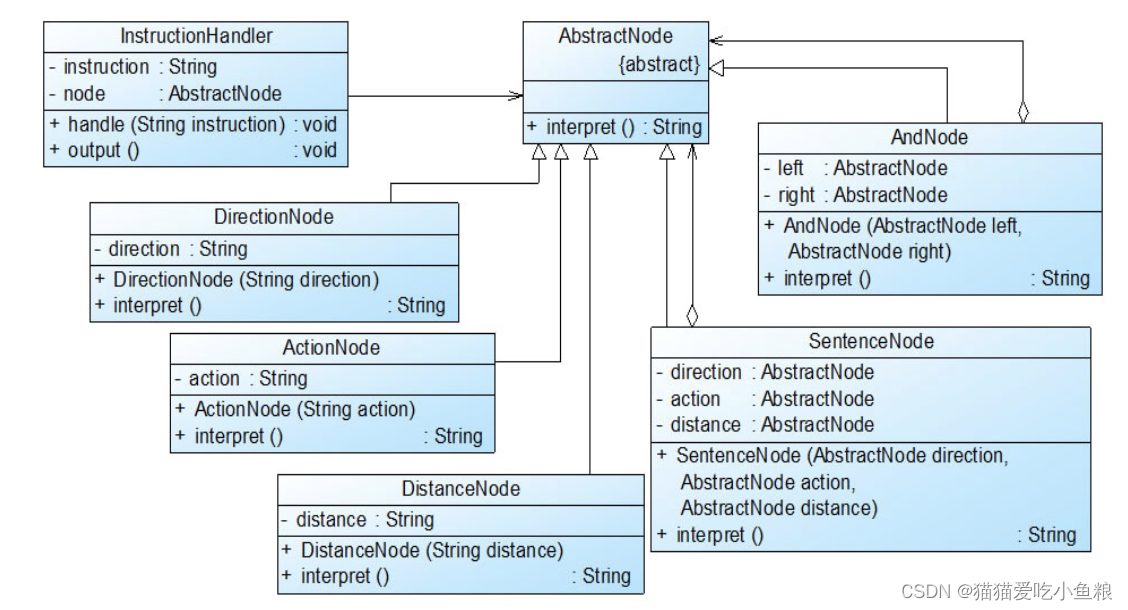
设计模式之解释器模式(上)
解释器模式 1)概述 1.定义 定义一个语言的文法,并且建立一个解释器来解释该语言中的句子,这里的“语言”是指使用规定格式和语法的代码。 2.结构图 3.角色 AbstractExpression(抽象表达式):在抽象表达…...

[23年蓝桥杯] 买二赠一
题目描述 【问题描述】 某商场有 N 件商品,其中第 i 件的价格是 A i 。现在该商场正在进行 “ 买二 赠一” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P (如果两件商品价格一样, 则…...

PgSQL的with as语法
returning 返回的这一些字段,然后进行汇总为remove_alarms 然后select一下remove_alarms 出来的数据然后保存到tb_alarm_his 里面 with remove_alarms as( delete fromtb_alarm whereid in (508) returning 0,now(),admin,alarmadvice,alarmadvicecn,alarmarises…...

六、c++代码中的安全风险-fopen
(misc) fopen: Check when opening files - can an attacker redirect it (via symlinks), force the opening of special file type (e.g., device files), move things around to create a race condition, control its ancestors, or change its contents? (CWE-362). 为…...
uniapp项目问题及解决(前后端互联)
1.路由跳转的问题 uni.navigateTo() 保留当前页面,跳转到应用内的某个页面,使用uni.navigateBack可以返回到原页面 uni.redirectTo() 关闭当前页面,跳转到应用内的某个页面。 uni.reLaunch&…...
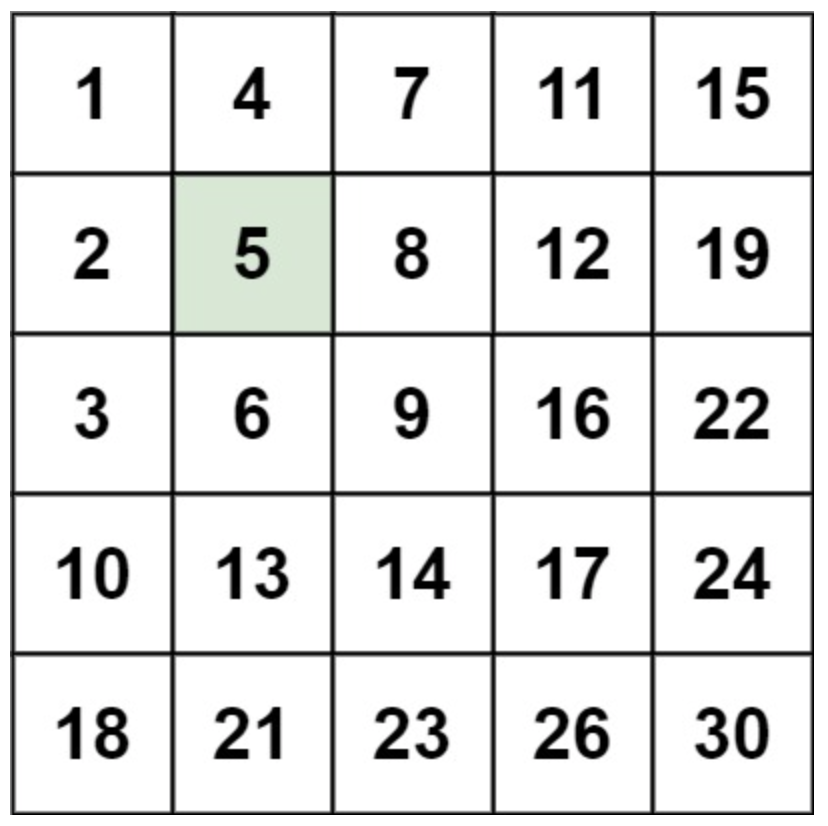
面试算法-154-搜索二维矩阵 II
题目 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。 每列的元素从上到下升序排列。 示例 1: 输入:matrix [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,…...

Java中Stream流介绍
Java 8引入的Stream API是Java中处理集合的一种高效方式,它提供了一种高级的迭代方式,允许你以声明式方式处理数据。Stream API可以对数据执行复杂的查询操作,而不需要编写冗长且复杂的循环语句。下面是一些使用Stream API的常见场景和示例&a…...

深度学习的层、算子和函数空间
目录 一、层、算子和函数空间概念 二、层(Layers) 三、算子(Operators) 3.1常见算子 3.2常见算子的性质 四、函数空间(Function Space) 一、层、算子和函数空间概念 层(Layers)…...

Pillow教程11:九宫格切图的实现方法(安排!!!)
---------------Pillow教程集合--------------- Python项目18:使用Pillow模块,随机生成4位数的图片验证码 Python教程93:初识Pillow模块(创建Image对象查看属性图片的保存与缩放) Pillow教程02:图片的裁…...

Macos 部署自己的privateGpt(2024-0404)
Private Chatgpt 安装指引 https://docs.privategpt.dev/installation/getting-started/installation#base-requirements-to-run-privategpt 下载源码 git clone https://github.com/imartinez/privateGPT cd privateGPT安装软件 安装: Homebrew /bin/bash -c…...

先安装CUDA后安装Visual Studio的额外配置
VS新建项目中增加CUDA选项 以vs2019 cuda 11.3为例 关闭vs2019解压cuda的windows安装包cuda_11.3.0_465.89_win10.exe进入路径cuda_11.3.0_465.89_win10\visual_studio_integration\CUDAVisualStudioIntegration\extras\visual_studio_integration\CudaProjectVsWizards\拷贝…...

2024 蓝桥打卡Day35
20240407蓝桥杯备赛 1、学习蓝桥云课省赛冲刺课 【3-搜索算法】【4-枚举与尺度法】2、学习蓝桥云课Java省赛无忧班 【1-语言基础】3、代码练习数字反转数字反转优化算法sort排序相关String字符串相关StringBuilder字符串相关HashSet相关 1、学习蓝桥云课省赛冲刺课 【3-搜索算法…...
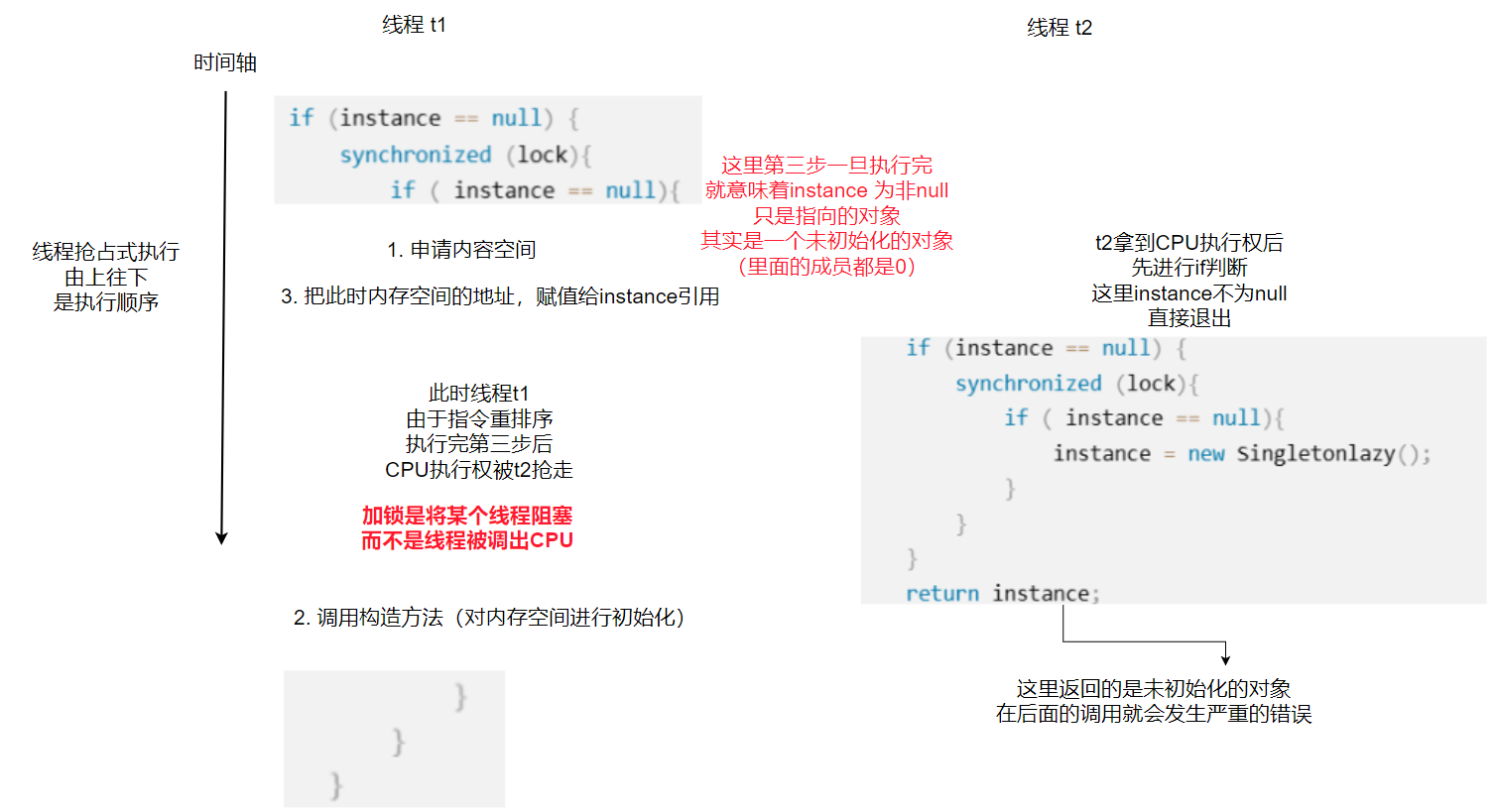
【Java】单例模式
单例模式是面试中常考的设计模式之一 在面试中,面试官常常会要求写出两种类型的单例模式并解释原理 本文中,将从0到1的介绍单例模式究竟是什么 文章目录 ✍一、什么是设计模式?✍二、单例模式是什么?✍三、单例模式的类型**1.饿汉…...

Linux|从 STDIN 读取 Awk 输入
简介 在之前关于 Awk 工具的系列文章中,主要探讨了如何从文件中读取数据。但如果你希望从标准输入(STDIN)中读取数据,又该如何操作呢? 在本文中,将介绍几个示例,展示如何使用 Awk 来过滤其他命令…...

关于K8S集群中maste节点r和worker节点的20道面试题
1. 什么是Kubernetes(K8S)? Kubernetes(通常简称为K8S)是一种开源的容器编排平台,用于自动化部署、扩展和管理容器化应用程序。以下是Kubernetes的一些核心特性和优势: 自动化部署和扩展&…...

基于 OpenHarmony HistogramComponent 柱状图开发指南
1. HistogramComponent 组件功能介绍 1.1. 功能介绍 应用开发过程,用鸿蒙提供的 Component 自定义柱状图效果。 HistogramComponent 组件可以更快速实现一个简单的柱状图功能。 HistogramComponent 对外提供数据源,修改柱状图颜色,间距的…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
