算法刷题应用知识补充--基础算法、数据结构篇
这里写目录标题
- 枚举
- 结
- 排序
- 结
- 模拟
- 结
- 二分
- 题
- 结
- 高精度
- 加、乘
- 题
- 结
- 减
- 题
- 结
- 除
- 题
- 结
- 结
- 位运算(均是拷贝运算,不会影响原数据,这点要注意)
- &、|、^
- 位运算特性+细节
- 知识补充
- 对于n-1的理解
- 异或来实现数字交换
- 找到只出现一次的数据,其余数据出现偶数次
- >> 、<<
- 二进制中相邻的位的特点
- 找出某个排列的所有子集
- 栈
- 题
- 结
- 单链表
- 题
- 结
- 双链表
- 题
- 结
- 队列
- 二级目录
- 二级目录
- 哈希表
- 题
- 结
- 字符串哈希
- 题
- 结
枚举
结
此类题就是暴力解法即可,大部分需要枚举题目范围的所有情况
排序
结
使用算法sort即可
模拟
结
题目说啥,我们做啥,就按照题目描述来
二分
题

结
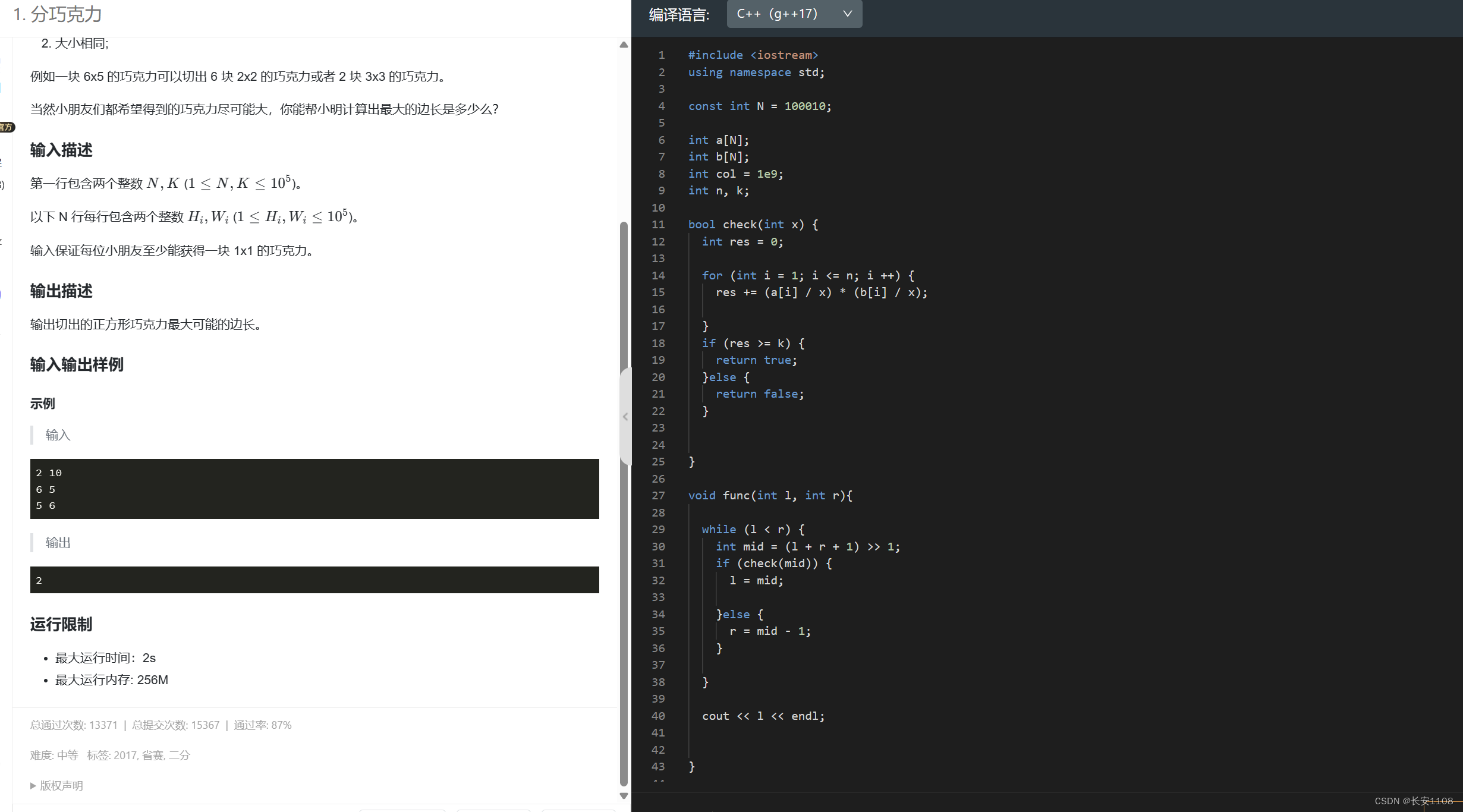
二分,就是对于一组单调的数据,两边的性质不同,二分可以找到某一边性质的最值,
如果找红色区间,则会找到满足红色性质的最大值(如果是红色区间,mid =( l + r + 1) >> 1)
如果找绿色区间,则会找到满足绿色性质的最小值(绿色区间则正常,mid = (l + r) >> 1)
补充:如果出错了,考虑check函数是否写错,是否疏忽了一些情况,比如此题,题目并没有说所有的巧克力原料都要用,所以,直接判断遍历所有的边长,如果有些边长比x小,则算出来是0,表示不使用该巧克力
注意点:最后 L == R 跳出循环,注意,最后有用的不是在循环中定义的那个mid,而是L R 或者num[L] num[R]
高精度
加、乘
题


结
二者的核心思想都是根据遍历,将当前位的运算都加到 t 身上,之后push(t % 10),然后更新 t = t / 10(这一步很精妙,表示如果 t
小于10,那么就不用进位,如果不是,那么就拿出其十位,加到 t ,为下一位的计算储备材料)
不同的是:加法最后如果 t 不为0,则补1,乘法则补 t
减
题

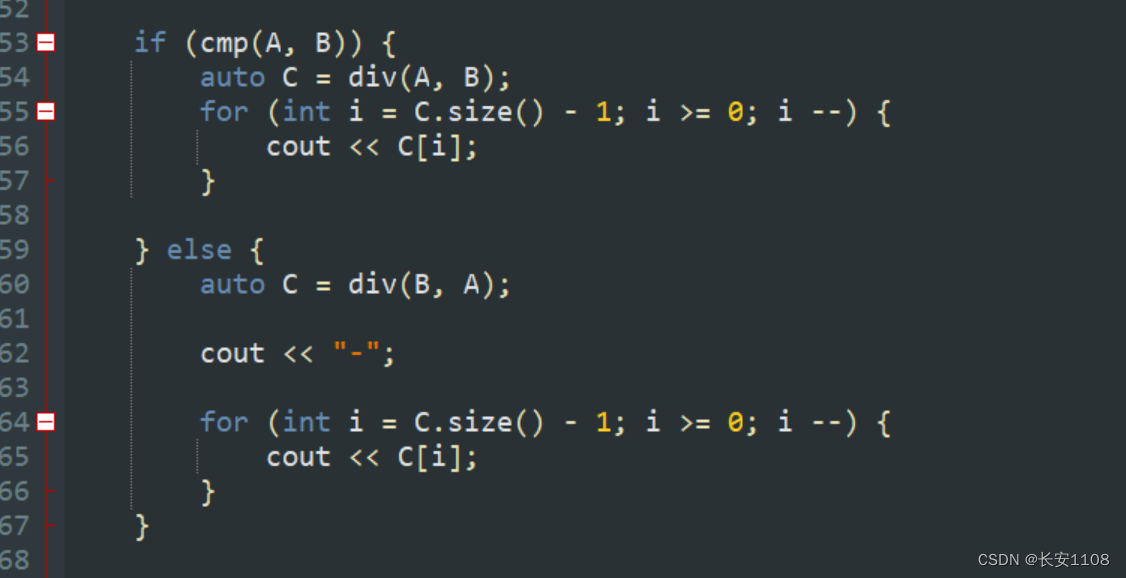
减法要先进行A 和 B的大小判断,看是A大还是B大,我们统一假设A大,也就是A大的话返回true,所以才会有上面的函数,且最后如果if和for都没有返回的话,最后返回true,表示A==B,所以相等的情况我们也是返回true,所以,该函数是判断是否A>=B
将大的传入div函数:(且如果题目规定求A-B,但是我们判断出B比A大,那么我们还是将B、A传入,最后输出的时候输出负号即可)
结
该题目也是,每次根据情况,将当前位的数 全部给到 t ,之后压入直接压t小于0的情况:(t + 10)% 10
之后判断t是不是真的小于0,如果是,那么 t 赋值为1,如果不是,那么 t 拨乱反正,改回0
最后要去除前导0
除
题

除法有三个参数,第三个参数是余数,且是引用,说明可以通过引用来返回余数是多少
且除法与其他不同,其他的函数内都是从0开始,这里是从后面开始,因为存入时,数据的高位在后面,除法要从高位开始
之后,是将所有的当前的数据加到 r 身上,然后push(r / b),且更新 r = r % b(更新余数)
最后要将其倒序,要将数据的高位放到容器末尾,这样方便去除前导0

传入时,由于第三个参数是传出参数,所以直接传入一个int型变量即可
结
且除法与其他不同,其他的函数内都是从0开始,这里是从后面开始,因为存入时,数据的高位在后面,除法要从高位开始
之后,是将所有的当前的数据加到 r 身上,然后push(r / b),且更新 r = r % b(更新余数)
最后要将其倒序,要将数据的高位放到容器末尾,这样方便去除前导0
main函数传参时:传入时,由于第三个参数是传出参数,所以直接传入一个int型变量即可
结
知识点1:他们都是根据具体情况,将当前的运算,全部存入 t 或者 r 中,然后拿着 t 或者 r 进行结果的压入,并更新 t 和 r,为下一次做准备
知识点2:加和乘法要额外注意,判断最后的 t ,如果循环结束,t还存在,那么要压入 1或者t
知识点3:减法和除法要额外注意,for循环之后,进行前导0的去除
知识点4:为了方便记忆以及前导0的去除,所以,我们统一在main函数,压入数据时,将数据的低位,先压入。也就是从string的末尾开始压入,表现为vector与string是反着的。
而输出时,由于我们统一将个位放在了C容器的栈底,所以,输出时,是从C容器的尾部开始输出
知识点五:在函数中,加减乘都是从个位开始计算,也就是for循环从0开始,而除是从高位开始计算,也就是从容器的末尾开始for循环,所以,在for循环结束后,要将其倒序,一方面是因为这样方便记忆,另一方面,这是去除前导0的前提要求
位运算(均是拷贝运算,不会影响原数据,这点要注意)
&、|、^
位运算特性+细节

首先,我们尝试不使用递归来解决这道题,他让我们判断是一个数是否为2的次幂。
尝试往位运算方面靠,位运算是通过二进制来解决问题的,而二进制就是2的次幂的表示,且,二进制从低位向高位,依次是2的012345…次方,所以,我们可以知道二进制表示为10000的数,(即第一位是1,后面全是0的数)是2的次幂数
所以,初步的认知已经建立了。之后寻找位运算的特性,如果一个数是1000的话,那么0111 + 1 就是 1000,而1000与0111做位与运算,可以得到0000,所以可以通过该性质找到10000特点的数
注意点1:小于等于0的数,可以直接排除
注意点2:进行位运算时,要在做完位运算之后,加一层括号,因为位运算的优先级低于==
知识补充
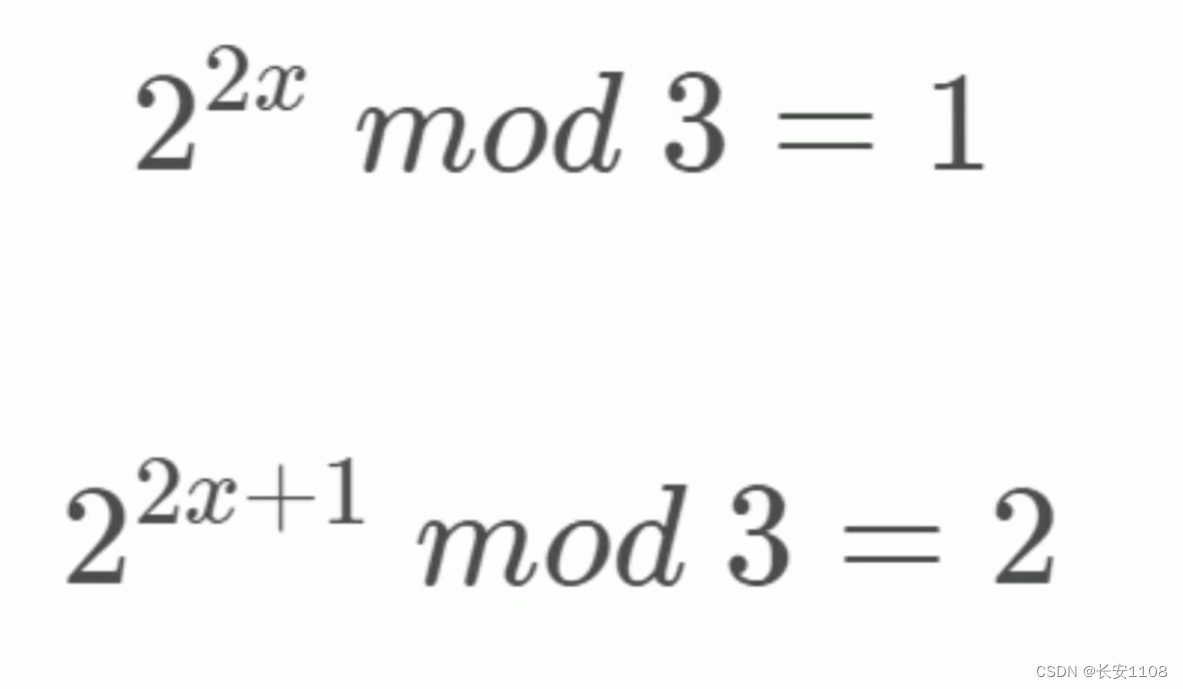
2的偶数次幂mod3等于1,例如4、16等,mod3 等于 1
而2的奇数次幂,就是2的偶数次幂再乘2,此时如8、32,mod3等于2
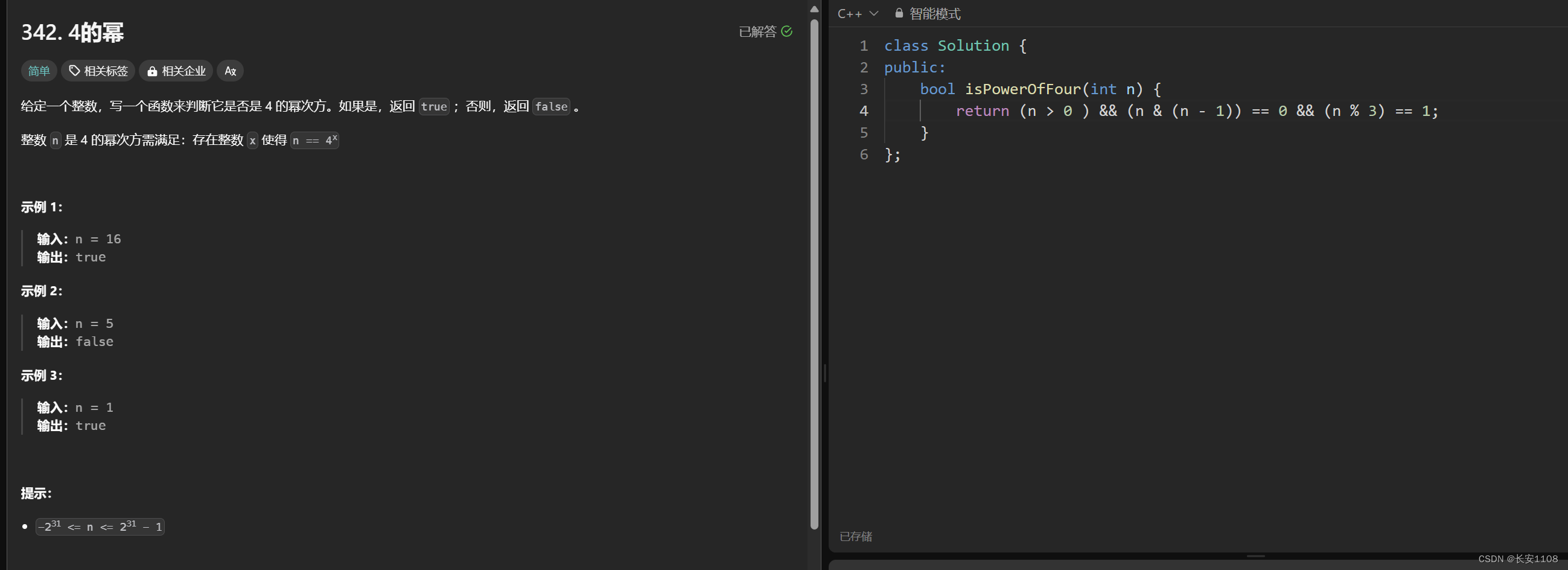
所以在求4的次幂时,因为2的偶次幂,一定是4的次幂,所以,我们在找到2的次幂数的基础上,再找到那些是2的偶次幂的数,那些数mod3==1
对于n-1的理解
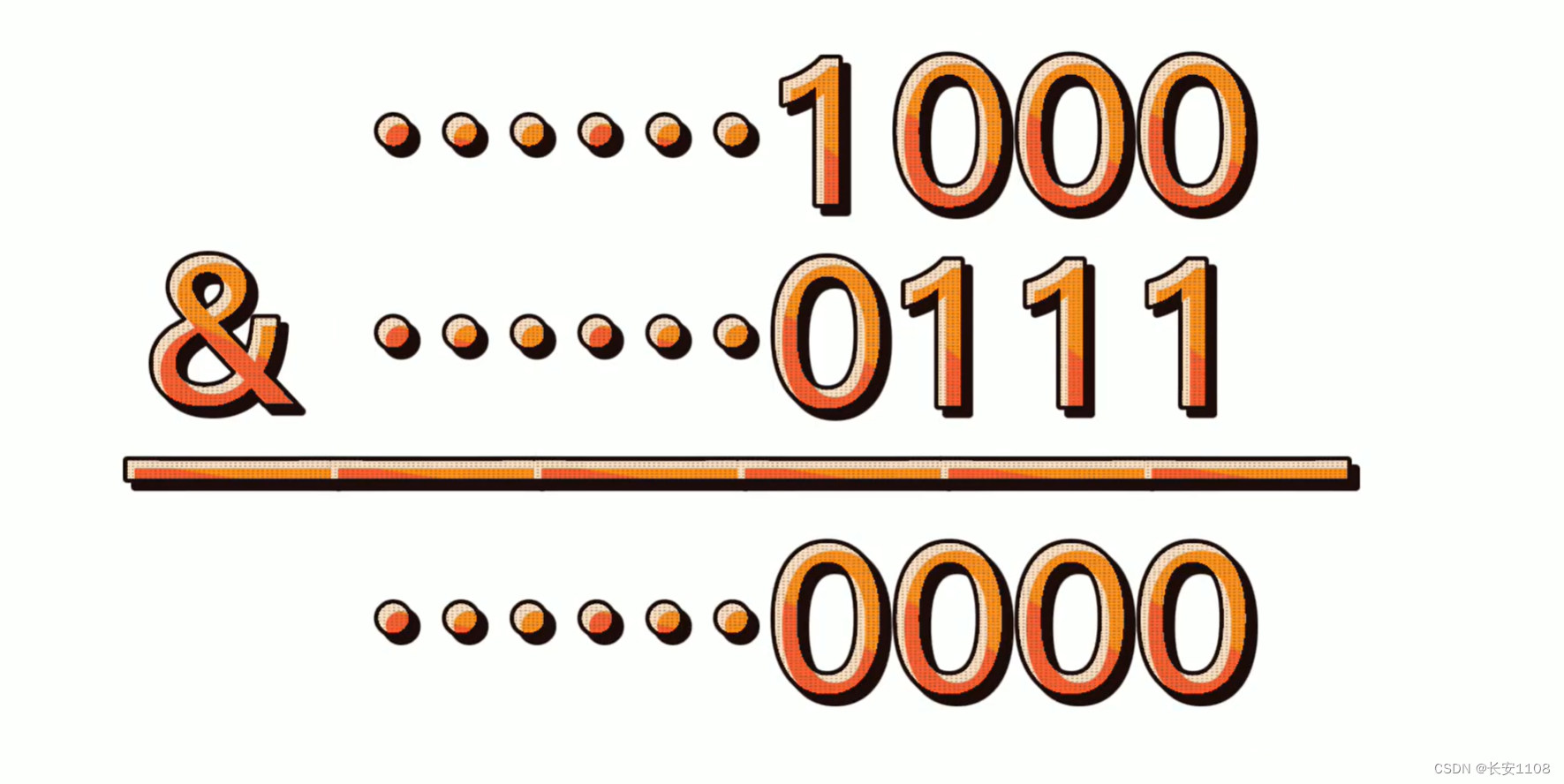
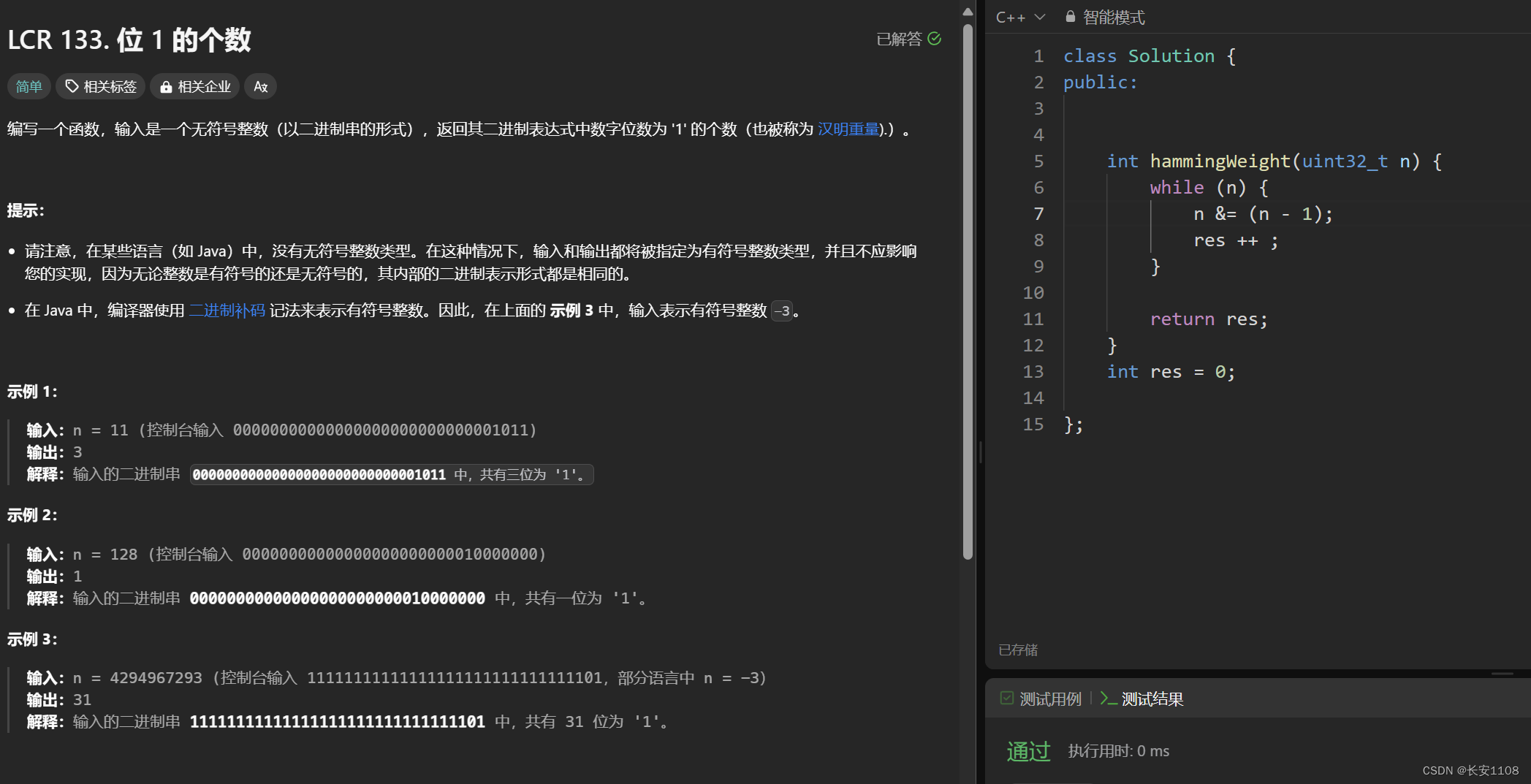
对于一个二进制 n = 10000010000101010,n - 1 = 10000010000101000,n - 1会将一个数的二进制表达最右边的1变为0,而其他不变,利用该特点可以得到1的个数
或者使用lowbit,见算法一栏“基础算法”(lowbit的时间复杂度更低)

异或来实现数字交换

首先,a = a ^ b,此后我们可以将一个a看成是变化之后的a,而如果a^b,则是原数据a、b
b = a ^ b,此时a是变化之后的a,将其拆开:a ^ b ^ b,此时a是变化之前的a,所以,就等于a ^ 0,最终等于原来的a
而到此时,a除了在第一行做出了改变,其他地方均无改变,所以,还是第一行的结论:可以将一个a看成是变化之后的a,而如果a^b,则是原数据a、b
所以,a = a ^ b,a是第一行代码执行后变化的a,b是原来的a,所以,将a拆开(得到原来的a 和 b)并且将b换成原来的a:a ^ b ^ a,再使用交换律,得到a ^ a ^ b,最后等于原来的b

找到只出现一次的数据,其余数据出现偶数次

首先定义res = 0;
之后将res与数组中的每个数进行异或运算
用到的知识点:
1、0^a = a
2、b^b = 0;
>> 、<<
二进制中相邻的位的特点


判断相邻位数是否交替为0、1
也就是相邻的位数上不能是相同的,即不能是00或者11,
而00对应于十进制是0,11对应于十进制是3
所以,如果 n&3 == 3,则表示当前n的右边两位是11
如果n&3 = = 0,则表示当前n的右边是00,(注意,此处还是&3,即00&11结果为00。逻辑上,他还有个等价式是00&00结果为11,也就是n&0 = = 3,但是如果&0的话,可能转为二进制就变成&一位0,而&3的话,铁定在二进制是&两位,所以,&0会导致某些数据点报错)
每次判断完之后,将n>>1右移一位,并覆盖到n,注意每次右移一位,如果右移两位,可能会出现0110,这样的数据,会出错
注意点1:&运算一次进行多位二进制判断时,尽量避免&0,尽可能找其等效式
注意点2:从此处我们也可以看出,我们之前的x&1,就是利用&的原始定义来求的,最终求出x二进制的个位,因为1表示成二进制就是…00001
找出某个排列的所有子集

我们以一个存有三个数的数组为例,那么nums.size()就等于3,而他的子集可能会是没有元素,或者一个元素,或者两个,或者三个,如果我们挨个遍历的话,时间复杂度肯定会剧增,所以,我们利用二进制,即利用位运算

我们可以将某个数在or不在,表示为二进制上的1or0,现在我们已经有了不同的子集与二进制的对应,那么如何进行遍历呢,我们可以让
i 从 0 遍历到 小于(1 << size()),因为1左移size位,就变成了1000,他正好就是四位的第一个数,所以小于他的,就是所有0位1位2位3位的二进制,也就是下图所示情况。这样,每个 i 的二进制,都标识了一种数组子集的情况


有了这些 i 的循环,我们如何判断当前是哪个二进制位上为1呢,我们可以在每个i循环步内,定义一个 j 循环,j 从 0 到小于size,
他实际上数组下标,判断 i & (1 << j)是否为1,而(1 << j)的循环是 001、010、100,如果结果不为0,那么就是为1,即当前循环步的 i的二进制标识,与当前 j 二进制中为1的那一位,都是1,即表明,i 中对应 j 为1 的位置是1,则nums[ size - j - 1 ]就是当前子集的元素之一
但是注意,他的顺序不是“先是单个元素,然后两个,三个”,他会先输出两个单元素,再输出一个双元素,再输出一个单元素,…无规则的,因为3对应二进制11,肯定会得到两个数
如果想要从左边开始判断,适当修改 i 和 j 的循环方向
栈
题

结
知识点1:tt初始化为0,那么栈顶元素就是从1开始,所以栈不为空的话,就是tt>0,而下标0的位置没有被使用
当然我们也可以使得tt初始化为-1,那么栈顶元素就是从0开始,tt>=0时,不空
知识点2:栈可以解决那些,需要一边进行输入一边进行匹配的问题
知识点3:注意特判,要保证 i > 0时,再进行check。所以说,有时候并不一定要设计出多优雅全能的代码,哪里有问题就解决哪里就好了
单链表
题

结
知识点1:主要就是将一些插入手法(头插、随机插),删除,初始化等等操作熟悉起来
知识点2:要注意初始化,如果一道题中,已知了链表的全貌,那么在一开始就可以把链表构造出来,head表示头指针,是头结点的下标。然后最后一个结点的ne数组值是-1
知识点3:如果后续还要有新的节点加入进来,那么初始化时,head就可以初始化为-1。后续有节点插入后,就会自然形成尾节点的ne数组值是-1
知识点4:注意遍历方式
知识点5:ne等这些与其他节点有联系的操作,都是通过下标联系,即地址,只有少数情况会用到e数值
注意点1:本题是在原本的链表内操作,在把x插到头结点的同时,还会把x从原来的地方删除,所以,每次操作涉及插入和删除两个动作
双链表
题

结
知识点1:因为链表的优越性,也就是其在物理位置上的顺序无所大谓,他的顺序是由指针域决定的,所以,我们会将e数组的0号位置设置为头结点,1号位置是尾节点,但是这两个点在e数组上并没有值,他们仅仅代表头指针和尾指针所指的位置,且对于双链表,我们设置了l【】和r【】数组,所以,初始化时,r[0] = 1, l[1] = 0,表示头指针位置指向尾指针位置,尾指针位置指向头指针位置
知识点2:

在k的右边插入:顺序是:
先新建一个结点,之后设置新节点的r 和 l (因为这个比较好设置)
其次,就是选择更新旧结点的r 和 l 了,但是如何选呢,有个好的记忆方法是,因为让我们在k的右边插入,所以,r[k] 是我们拿到右边旧结点的关键信息,他会贯穿整个过程,所以,他应该最后一个被更新,所以,在k的右边插入,就最后更新r[k]
知识点3:对于双向链表,插入是需要注意顺序的,但是删除不需要注意顺序
知识点4:对于双链表的遍历,从 i = r[0]开始,当 i != 1时,i = r[ i ]
注意循环条件不要写成r[ i ] != 1,这样的话,最后一个元素将不会输出
知识点5:至于要不要构建循环双链表,则视题目情况而定(构建方式,加一个l[0] = 1, r[1] = 0,其他操作不变)
队列
二级目录
二级目录
哈希表
题
结
可能是用于,处理一些集合,该集合的特点是,数据少,但是数据有很大的也有很小的,将其哈希到一个比较紧凑的区域,节省空间和效率
思考:有没有可能可以使用set or multiset代替?
字符串哈希
题

结
他主要是将前 i 个字符组成的子串哈希成一个ULL值,再根据【l, r】的哈希值是h[r] - h[l - 1]*p[r-(l - 1)]这个公式,从而可以迅速的求出任意一段子串
知识点1:该计算公式用于字符串从1位置开始存储,所以,我们在写程序时,要写从1开始输入字符串,但是如果题目要求从0开始输入,且题目据此规则进行查询,那么无需改动其他的,只需要在读入l1,r1,l2,r2后,传入get函数l1 + 1,r1 + 1,l2 + 1,r2 + 1,即可
知识点2:要注意大写P=131,小写p是数组,表示p的某次方
知识点3:预处理:初始化在全局位置,所以p[]和h[]都是0,在预处理之前,我们要修改p[0] = 1,不然所有的p都是0,h不用修改,预处理时,处理 i 从1到N(或者题目若给出了字符串长度n,则是到等于n,如果拿不准,直接N也可以),注意p和h的预处理都建立在i - 1之上,别写错了
知识点4:h数组和p数组都是ULL,对于无符号整形的变量,如果超出了其表示范围,那么会对其进行自动取模,所以,这里存入ULL类型,是为了自动取模2的64次方(该自动取模只会使用与无符号整型,且如果遇到负数 则还会将其先加上模数变为整数 再取模)
相关文章:

算法刷题应用知识补充--基础算法、数据结构篇
这里写目录标题 枚举结 排序结 模拟结 二分题结 高精度加、乘题结 减题结 除题结 结 位运算(均是拷贝运算,不会影响原数据,这点要注意)&、|、^位运算特性细节知识补充对于n-1的理解异或来实现数字交换找到只出现一次的数据&am…...

ngnix的反向代理是什么?有什么作用?
1、Nginx的反向代理是什么? Nginx的反向代理是一种网络架构模式,其中Nginx服务器作为前端服务器,接收客户端的请求,然后将这些请求转发给后端服务器(例如Java应用程序服务器)。在这个过程中,客…...

Windows程序设计课程作业-1
文章目录 1. 作业内容2. 设计思路分析与难点3. 代码实现3.1 接口定义3.2 工厂类实现3.3 委托和事件3.4 主函数3.5 代码运行结果 4. 代码地址5. 总结&改进思路6. 阅读参考 1. 作业内容 使用 C# 编码(涉及类、接口、委托等关键知识点),实现…...

2024年河北省网络建设与运维-省赛-nginx 和tomcat 服务服务步骤
题目: 5.nginx 和tomcat 服务 任务描述:利用系统自带tomcat,搭建 Tomcat网站。 (1)配置 linux2 为 nginx 服务器,网站目录为/www/nginx,默认文档 index.html 的内容为“HelloNginx”…...
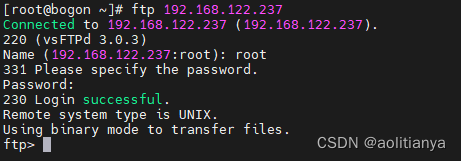
CentOS下部署ftp服务
要在linux部署ftp服务首先需要安装vsftpd服务 yum install vsftpd -y 安装完成后需要启动vsftpd服务 systemctl start vsftpd 为了能够访问ftp的端口,需要在防火墙中开启ftp的端口21,否则在使用ftp连接的时候会报错No route to host. 执行如下命令为f…...
伦敦银几点开盘?为什么交易不了?
近期是西方的假期,伦敦银市场因而休市。很多朋友看到之前伦敦银上涨那么厉害,正摩拳擦掌准备入场大展拳脚,然而现在却吃了一个大瘪:怎么我刚准备好大展拳脚,结果却没有开盘呢?到底伦敦银几点开盘࿱…...

快手开放平台对接内容管理demo
其中包括用户授权,获取accessToken,获取用户信息,自动上传视频,发布视频,视频列表,删除视频等 <?php namespace app\controller;use app\BaseController; use think\Exception; use think\facade\App;…...

2024年32款数据分析工具分五大类总览
数据分析工具在现代商业和科学中扮演着不可或缺的角色,为组织和个人提供了深入洞察和明智决策的能力。这些工具不仅能够处理大规模的数据集,还能通过强大的分析和可视化功能揭示隐藏在数据背后的模式和趋势。数据分析工具软件主要可以划分为以下五个类别…...
WPS的JS宏如何批量实现文字的超链接
表格中需要对文字进行超链接,每个链接指引到不同的地址。例如: 实现如下表格中,文件名称超级链接到对应的文件路径上,点击对应的文件名称,即可打开对应的文件。 序号文件名称文件路径1变更申请与处理表.xls文档\系统…...

0203逆矩阵-矩阵及其运算-线性代数
文章目录 一、逆矩阵的定义、性质和求法二、逆矩阵的初步应用结语 一、逆矩阵的定义、性质和求法 定义7 对于 n n n阶矩阵A,如果有一个 n n n阶矩阵B,使 A B B A E ABBAE ABBAE 则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆…...
加州大学欧文分校英语基础语法专项课程03:Simple Past Tense 学习笔记(完结)
Learn English: Beginning Grammar Specialization Specialization Certificate course 3: Simple Past Tense Course Certificate 本文是学习 https://www.coursera.org/learn/simple-past-tense 这门课的学习笔记,如有侵权,请联系删除。…...
基于Java微信小程序的医院挂号小程序,附源码
博主介绍:✌IT徐师兄、7年大厂程序员经历。全网粉丝15W、csdn博客专家、掘金/华为云//InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇dz…...

7.网络编程-安全
目录 引言 Session Cookie JWT (JSON Web Token) 网络攻击 CSRF DDoS 其他常见网络攻击类型及应对措施 引言 Session、Cookie 和 JWT 都是Web开发中用于实现用户状态管理和身份验证的技术。它们各自有不同的特点和应用场景: Session Session 是一种服务器…...

信息泄露漏洞的JS整改方案
引言 🛡️ 日常工作中,我们经常会面临线上环境被第三方安全厂商扫描出JS信息泄露漏洞的情况,这给我们的系统安全带来了潜在威胁。但幸运的是,对于这类漏洞的整改并不复杂。本文将介绍几种可行的整改方法,以及其中一种…...

WKWebView的使用
一、简介 在iOS中,WKWebView是WebKit框架提供的一个用于展示网页内容的控件,相比UIWebView有更好的性能和功能。 以下是在iOS中使用WKWebView的基本步骤: 1.1 导入WebKit框架 import WebKit1.2 创建WKWebView实例 let webView WKWebVie…...

iOS MT19937随机数生成,结合AES-CBC加密算法实现。
按处理顺序说明: 1. 生成随机数序列字符串函数 生成方法MT19937,初始种子seed,利用C库方法,生成: #include <random> //C 库头文件引入NSString * JKJMT19937Seed(uint32_t seed) {NSLog("MT19937Seed种…...

阿里云2024年优惠券获取方法及使用教程详解
阿里云是阿里巴巴集团旗下的云计算服务提供商,是全球领先的云计算及人工智能科技公司之一。提供免费试用、云服务器、云数据库、云安全、云企业应用等云计算服务,以及大数据、人工智能服务、精准定制基于场景的行业解决方案。 阿里云2024年优惠券的获取方…...

hadoop中hdfs的fsimage文件与edits文件
hadoop中hdfs的fsimage文件与edits文件的作用 首先,我们抛出fsimage和edits文件的功能描述。 Fsimage文件: HDFS文件系统元数据的一个永久性的检查点,其中包含HDFS文件系统的 所有目录和文件inode的序列化信息。 Edits文件:存放HDFS文件系统的所有更…...

最新版两款不同版SEO超级外链工具PHP源码
可根据个人感觉喜好自行任意选择不同版本使用(版V1或版V2) 请将zip文件全部解压缩即可访问! 源码全部开源,支持上传二级目录访问 已更新增加大量高质量外链(若需要增加修改其他外链请打开txt文件)修复优…...

.net框架和c#程序设计第二次测试
一、实验内容 1、设计一个用户登录页面webform1.aspx,效果如下图所示: 2、点击webform1.aspx中“还未注册”连接进入register.aspx,注册页面效果如下图所示:点击用户注册信息到usershow.aspx页面,并显示注册的用户信息…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
