LeetCode笔记——1042.不邻接植花
题目
有 n 个花园,按从 1 到 n 标记。另有数组 paths ,其中 paths[i] = [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中,你打算种下四种花之一。
另外,所有花园 最多 有 3 条路径可以进入或离开.
你需要为每个花园选择一种花,使得通过路径相连的任何两个花园中的花的种类互不相同。
以数组形式返回 任一 可行的方案作为答案 answer,其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1、2、3、4 表示。保证存在答案。
示例 1:
输入:n = 3, paths = [[1,2],[2,3],[3,1]]
输出:[1,2,3]
解释:
花园 1 和 2 花的种类不同。
花园 2 和 3 花的种类不同。
花园 3 和 1 花的种类不同。
因此,[1,2,3] 是一个满足题意的答案。其他满足题意的答案有 [1,2,4]、[1,4,2] 和 [3,2,1]
示例 2:
输入:n = 4, paths = [[1,2],[3,4]]
输出:[1,2,1,2]
思路
1.暴力遍历所有花园的路径,顺序选择花直到出现可选的花。
2.利用哈希表存储花园的路径,顺序遍历n个花园,选择相邻花园已种的下一种花。
C#源码
方法一
public class Solution {public int[] GardenNoAdj(int n, int[][] paths) {int[] arrAns = new int[n];int floweTypes = 4;//遍历花园for (int i = 0; i < n; i++) {//尝试选择for (int j = 1; j <= floweTypes; j++) {if (IsTryChoose(i, j, arrAns, paths)) {arrAns[i] = j; // 选择成功break;}}}return arrAns;}bool IsTryChoose(int garden, int type, int[] arrAns, int[][] paths){foreach (int[] path in paths) {int now = path[0] - 1, next = path[1] - 1;//判断相邻花园是否已选该花,已选则返回falseif (now == garden && arrAns[next] == type)return false;if (next == garden && arrAns[now] == type) return false;}return true;}
}
方法二
public class Solution {public int[] GardenNoAdj(int n, int[][] paths) {Dictionary<int, List<int>> dicGardens = new Dictionary<int, List<int>>();for(int i = 0; i < n; i++){dicGardens[i] = new List<int>(); //创建每个花园记录路径列表,key:花园,value:路径}foreach(int[] path in paths){//记录路径int start = path[0] - 1, end = path[1] - 1;if(start < end)dicGardens[end].Add(start);elsedicGardens[start].Add(end);}//遍历相邻花园计算可选的花int[] arrAns = new int[n];foreach (var item in dicGardens) {int garden = item.Key;List<int> listGardenPath = item.Value;bool[] arrIsTypeUsed = new bool[5]; //1-4代表不同种花foreach(int currentGarden in listGardenPath){int tempType = arrAns[currentGarden]; //记录已选的花arrIsTypeUsed[tempType] = true;}int chooseType = 1;//判断相邻花园是否已选该花,已选则选择下一种花,避免相邻花园同样花while(arrIsTypeUsed[chooseType]){chooseType++;}arrAns[garden] = chooseType;}return arrAns;}
}
来源:力扣(LeetCode)
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
相关文章:

LeetCode笔记——1042.不邻接植花
题目 有 n 个花园,按从 1 到 n 标记。另有数组 paths ,其中 paths[i] [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中,你打算种下四种花之一。 另外,所有花园 最多 有 3 条路径可以进入或离开. 你需要为每个花园…...

Centos7搭建 Skywalking 单机版
介绍 Skywalking是应用性能监控平台,可用于分布式系统,支持微服务、云原生、Docker、Kubernetes 等多种架构场景。 整体架构如图 Agent :在应用中,收集 Trace、Log、Metrics 等监控数据,使用 RPC、RESTful API、Kafk…...

定制您的设备体验:如何更改Android启动动画
“bootanim"通常是指在操作系统启动过程中显示的动画,尤其是在移动设备或某些定制的Linux发行版中较为常见。这个术语并不是一个标准的命令或工具名称,而是通常用来描述"启动动画”(boot animation)的简称。在Android设备中,启动动…...

Docker日常系列
一、如何build双架构(AMDRAM)镜像 (1) 需求描述 当k8s集群的硬件资源为ARMAMD混合架构时,镜像需要同时支持2种架构,如何构建镜像。 (2) 操作 准备工作:需要将代码在不同架构下build为镜像,以下默认我们…...

Midjourney该怎么用?从零基础到落地实践
前言 从注册登录到基本的操作界面,提示词组成后缀介绍,到主流的生成图片的方式,以及最重要的提示词咒语分享,还有一些我的使用心得,希望对大家有帮助! 喜欢的话欢迎关注我,欢迎点赞收藏评论&am…...
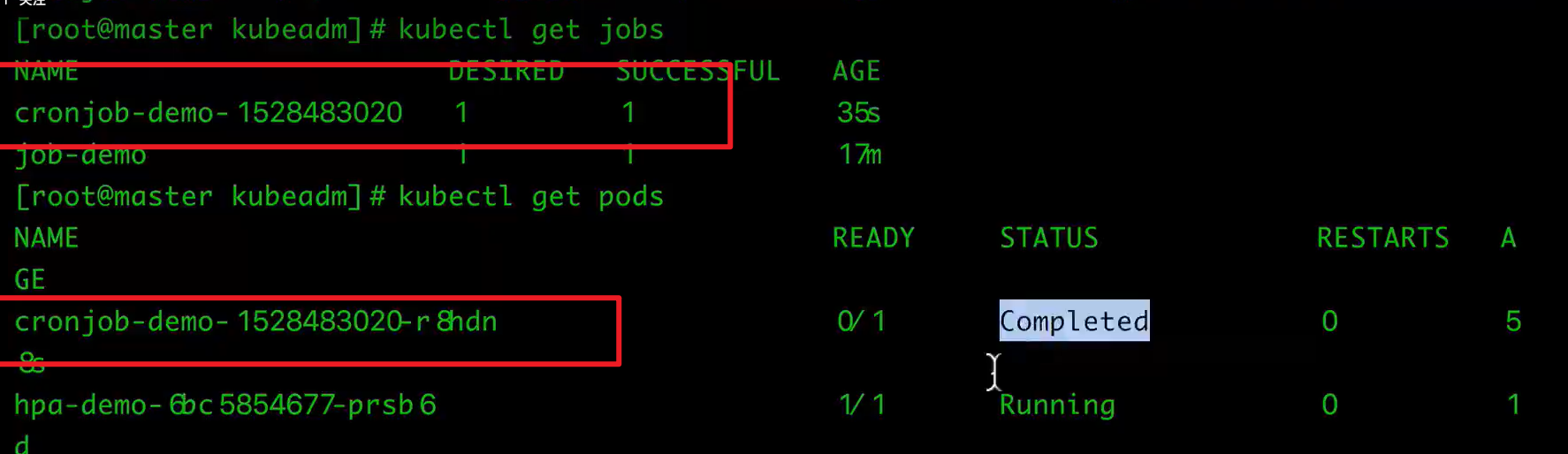
K8S:常用资源对象操作
文章目录 一、使用Replication Controller(RC)、Replica Set(RS) 管理Pod1 Replication Controller(RC)2 Replication Set(RS) 二、Deployment的使用1 创建2 滚动升级3 回滚Deployment三、 Pod 自动扩缩容HPA1 使用kubectl autosc…...

算法刷题应用知识补充--基础算法、数据结构篇
这里写目录标题 枚举结 排序结 模拟结 二分题结 高精度加、乘题结 减题结 除题结 结 位运算(均是拷贝运算,不会影响原数据,这点要注意)&、|、^位运算特性细节知识补充对于n-1的理解异或来实现数字交换找到只出现一次的数据&am…...

ngnix的反向代理是什么?有什么作用?
1、Nginx的反向代理是什么? Nginx的反向代理是一种网络架构模式,其中Nginx服务器作为前端服务器,接收客户端的请求,然后将这些请求转发给后端服务器(例如Java应用程序服务器)。在这个过程中,客…...

Windows程序设计课程作业-1
文章目录 1. 作业内容2. 设计思路分析与难点3. 代码实现3.1 接口定义3.2 工厂类实现3.3 委托和事件3.4 主函数3.5 代码运行结果 4. 代码地址5. 总结&改进思路6. 阅读参考 1. 作业内容 使用 C# 编码(涉及类、接口、委托等关键知识点),实现…...

2024年河北省网络建设与运维-省赛-nginx 和tomcat 服务服务步骤
题目: 5.nginx 和tomcat 服务 任务描述:利用系统自带tomcat,搭建 Tomcat网站。 (1)配置 linux2 为 nginx 服务器,网站目录为/www/nginx,默认文档 index.html 的内容为“HelloNginx”…...
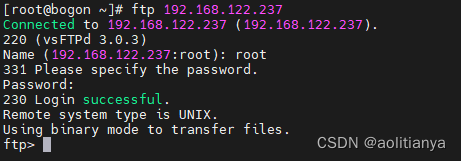
CentOS下部署ftp服务
要在linux部署ftp服务首先需要安装vsftpd服务 yum install vsftpd -y 安装完成后需要启动vsftpd服务 systemctl start vsftpd 为了能够访问ftp的端口,需要在防火墙中开启ftp的端口21,否则在使用ftp连接的时候会报错No route to host. 执行如下命令为f…...
伦敦银几点开盘?为什么交易不了?
近期是西方的假期,伦敦银市场因而休市。很多朋友看到之前伦敦银上涨那么厉害,正摩拳擦掌准备入场大展拳脚,然而现在却吃了一个大瘪:怎么我刚准备好大展拳脚,结果却没有开盘呢?到底伦敦银几点开盘࿱…...

快手开放平台对接内容管理demo
其中包括用户授权,获取accessToken,获取用户信息,自动上传视频,发布视频,视频列表,删除视频等 <?php namespace app\controller;use app\BaseController; use think\Exception; use think\facade\App;…...

2024年32款数据分析工具分五大类总览
数据分析工具在现代商业和科学中扮演着不可或缺的角色,为组织和个人提供了深入洞察和明智决策的能力。这些工具不仅能够处理大规模的数据集,还能通过强大的分析和可视化功能揭示隐藏在数据背后的模式和趋势。数据分析工具软件主要可以划分为以下五个类别…...
WPS的JS宏如何批量实现文字的超链接
表格中需要对文字进行超链接,每个链接指引到不同的地址。例如: 实现如下表格中,文件名称超级链接到对应的文件路径上,点击对应的文件名称,即可打开对应的文件。 序号文件名称文件路径1变更申请与处理表.xls文档\系统…...

0203逆矩阵-矩阵及其运算-线性代数
文章目录 一、逆矩阵的定义、性质和求法二、逆矩阵的初步应用结语 一、逆矩阵的定义、性质和求法 定义7 对于 n n n阶矩阵A,如果有一个 n n n阶矩阵B,使 A B B A E ABBAE ABBAE 则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆…...
加州大学欧文分校英语基础语法专项课程03:Simple Past Tense 学习笔记(完结)
Learn English: Beginning Grammar Specialization Specialization Certificate course 3: Simple Past Tense Course Certificate 本文是学习 https://www.coursera.org/learn/simple-past-tense 这门课的学习笔记,如有侵权,请联系删除。…...
基于Java微信小程序的医院挂号小程序,附源码
博主介绍:✌IT徐师兄、7年大厂程序员经历。全网粉丝15W、csdn博客专家、掘金/华为云//InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇dz…...

7.网络编程-安全
目录 引言 Session Cookie JWT (JSON Web Token) 网络攻击 CSRF DDoS 其他常见网络攻击类型及应对措施 引言 Session、Cookie 和 JWT 都是Web开发中用于实现用户状态管理和身份验证的技术。它们各自有不同的特点和应用场景: Session Session 是一种服务器…...

信息泄露漏洞的JS整改方案
引言 🛡️ 日常工作中,我们经常会面临线上环境被第三方安全厂商扫描出JS信息泄露漏洞的情况,这给我们的系统安全带来了潜在威胁。但幸运的是,对于这类漏洞的整改并不复杂。本文将介绍几种可行的整改方法,以及其中一种…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
