AcWing---乌龟棋---线性dp

312. 乌龟棋 - AcWing题库
思路:
原来没有碰到过类似的题:
- dp数组为思维:dp[i][j][k][r],分别表示用了i个第一类型卡片,j个第二类型卡片...所到的格子数的最大分数,为啥不用记录乌龟到了哪里呢?因为i*1+j*2+k*3+r*4已经表明了小乌龟的终点位置了。
- 状态转移方程式dp[i][j][k][r]=max(dp[i-1][j][k][r],dp[i][j-1][k][r],...)+a[i*1+j*2+k*3+r*4]
- 数组初始化:dp[0][1][2][3]=0
C++代码:
#include<bits/stdc++.h>
using namespace std;int g[41][41][41][41];
int n,m;
int a[400];
int b[5];int main(){cin>>n>>m;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<m;i++){int temp;cin>>temp;b[temp]++;}g[0][0][0][0]=a[0];for(int i=0;i<=b[1];i++){for(int j=0;j<=b[2];j++){for(int k=0;k<=b[3];k++){for(int r=0;r<=b[4];r++){if(i-1>=0){g[i][j][k][r]=max(g[i][j][k][r],g[i-1][j][k][r]+a[i+2*j+3*k+4*r]);}if(j-1>=0){g[i][j][k][r]=max(g[i][j][k][r],g[i][j-1][k][r]+a[i+2*j+3*k+4*r]);}if(k-1>=0){g[i][j][k][r]=max(g[i][j][k][r],g[i][j][k-1][r]+a[i+2*j+3*k+4*r]);}if(r-1>=0){g[i][j][k][r]=max(g[i][j][k][r],g[i][j][k][r-1]+a[i+2*j+3*k+4*r]);}}}}}cout<<g[b[1]][b[2]][b[3]][b[4]];return 0;
}python代码:
n,m=map(int,input().split())
a=list(map(int,input().split()))
b_temp=list(map(int,input().split()))
b=[0]*5
for i in b_temp:b[i]+=1g=[[[[0 for _ in range(41)] for _ in range(41)] for _ in range(41)] for _ in range(41)]
g[0][0][0][0]=a[0]
for i in range(b[1]+1):for j in range(b[2]+1):for k in range(b[3]+1):for r in range(b[4]+1):if i-1>=0:g[i][j][k][r]=max(g[i][j][k][r],g[i-1][j][k][r]+a[i+j*2+k*3+r*4]);if j-1>=0:g[i][j][k][r]=max(g[i][j][k][r],g[i][j-1][k][r]+a[i+j*2+k*3+r*4]);if k-1>=0:g[i][j][k][r]=max(g[i][j][k][r],g[i][j][k-1][r]+a[i+j*2+k*3+r*4]);if r-1>=0:g[i][j][k][r]=max(g[i][j][k][r],g[i][j][k][r-1]+a[i+j*2+k*3+r*4]);
print(g[b[1]][b[2]][b[3]][b[4]])相关文章:

AcWing---乌龟棋---线性dp
312. 乌龟棋 - AcWing题库 思路: 原来没有碰到过类似的题: dp数组为思维:dp[i][j][k][r],分别表示用了i个第一类型卡片,j个第二类型卡片...所到的格子数的最大分数,为啥不用记录乌龟到了哪里呢࿱…...

python代码使用过程中使用快捷键注释时报错
1.代码 2.代码报错 3.代码注释后的结果 4. 原因...

go之web框架gin
介绍 Gin 是一个用 Go (Golang) 编写的 Web 框架。 它具有类似 martini 的 API,性能要好得多,多亏了 httprouter,速度提高了 40 倍。 如果您需要性能和良好的生产力,您一定会喜欢 Gin。 安装 go get -u github.com/gin-gonic/g…...
SpringBoot 定时任务实践、定时任务按指定时间执行
Q1. springboot怎样创建定时任务? 很显然,人人都知道,Scheduled(cron ".....") Q2. 如上所示创建了定时任务却未能执行是为什么? 如果你的cron确定没写错的话 cron表达式是否合法,可参考此处,…...

MYSQL数据库故障排除与优化
目录 MySQL 单实例故障排查 MySQL 主从故障排查 MySQL 优化 MySQL 单实例故障排查 故障现象 1 ERROR 2002 (HY000): Cant connect to local MySQL server through socket /data/mysql/mysql.sock (2) 问题分析:以上这种情况一般都…...
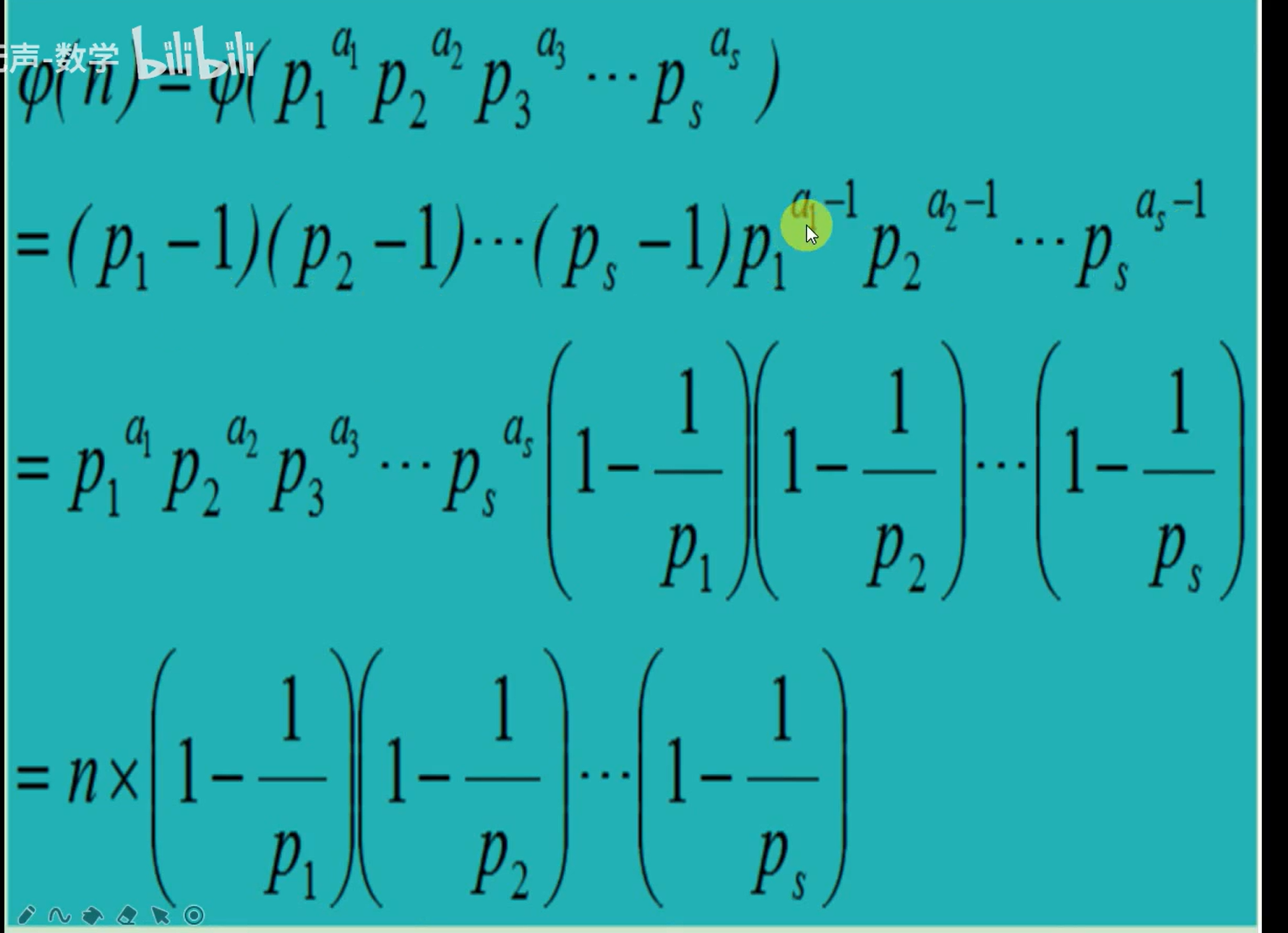
算法-数论-蓝桥杯
算法-数论 1、最大公约数 def gcd(a,b):if b 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b ! 0:cur aa bb cur%bpassreturn a欧几里得算法 a可以表示成a kb r(a,b,k,…...

222.完全二叉树节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最…...

C++中的string类操作详解
引言 针对C中的string,本文主要讲解如何对其进行插入、删除、查找、比较、截断、分割以及与数字之间的相互转换等。 字符串插入 1. append方法 std::string str "hello"; str.append(7, w); // 在末尾添加7个字符w str.append("wwwwwww");…...

Java绘图坐标体系
一、介绍 下图说明了Java坐标系。坐标原点位于左上角,以像素为单位。在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐…...
【MATLAB源码-第38期】基于OFDM的块状导频和梳状导频误码率性能对比,以及LS/LMMSE两种信道估计方法以及不同调制方式对比。
操作环境: MATLAB 2022a 1、算法描述 块状导频和梳状导频都是用于无线通信系统中信道估计的方法。 块状导频: 定义: 在频域上,块状导频是连续放置的一组导频符号。这意味着所有的导频符号都集中在一个短的时间段内发送。 优点…...
javaWeb车辆管理系统设计与实现
摘 要 随着经济的日益增长,车辆作为最重要的交通工具,在企事业单位中得以普及,单位的车辆数目已经远远不止简单的几辆,与此同时就产生了车辆资源的合理分配使用问题。 企业车辆管理系统运用现代化的计算机管理手段,不但可以对车辆的使用进行合理的管理,…...
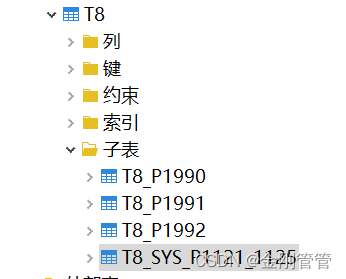
【DM8】间隔分区
是范围分区的一个扩展 如果使用了间隔函数做分区,在数据插入的时候,如果没有合适的分区,数据库会自动创建一个新的分区。 –year往后推两年 SELECT SYSDATE numtoyminterval(2,‘YEAR’); –month往后推两年 SELECT SYSDATE numtoyminterv…...

0基础如何进入IT行业?
目录 0基础如何进入IT行业? 一、学习路径 二、技能培养 三、实践经验 0基础如何进入IT行业? 对于没有任何相关背景知识的人来说,成功进入IT行业可能看起来是一个遥不可及的目标。然而,只要有正确的方法和坚持不懈的努力&#…...
C#将Console写至文件,且文件固定最大长度
参考文章 将C#的Console.Write同步到控制台和log文件输出 业务需求 在生产环境中,控制台窗口不便展示出来。 为了在生产环境中,完整记录控制台应用的输出,选择将其输出到文件中。 但是,一次性存储所有输出的话,文件会…...

《CSS 知识点》仅在文本有省略号时添加 tip 信息
html <div ref"btns" class"btns"><div class"btn" >这是一段很短的文本.</div><div class"btn" >这是一段很短的文本.</div><div class"btn" >这是一段很长的文本.有省略号和tip.<…...

彩虹聚合DNS管理系统v1.0全新发布
聚合DNS管理系统(https://github.com/netcccyun/dnsmgr)可以实现在一个网站内管理多个平台的域名解析,目前已支持的域名平台有:阿里云、腾讯云、华为云、西部数码、CloudFlare。本系统支持多用户,每个用户可分配不同的…...

3.10 Python数据类型转换
Python类型转换,Python数据类型转换函数大全 虽然 Python 是弱类型编程语言,不需要像Java或 C 语言那样还要在使用变量前声明变量的类型,但在一些特定场景中,仍然需要用到类型转换。 比如说,我们想通过使用 print() …...

Kotlin基础学习
Kotlin基础学习主要涵盖安装Kotlin编译器、了解基础语法、学习变量声明、类型推断、函数定义以及控制结构等方面。以下是一个简要的Kotlin基础学习指南: 一、安装Kotlin 首先,你需要从JetBrains的官方网站下载并安装Kotlin编译器。同时,你也…...
配置交换机 SSH 管理和端口安全——实验1:配置交换机基本安全和 SSH管理
实验目的 通过本实验可以掌握: 交换机基本安全配置。SSH 的工作原理和 SSH服务端和客户端的配置。 实验拓扑 交换机基本安全和 SSH管理实验拓扑如图所示。 交换机基本安全和 SSH管理实验拓扑 实验步骤 (1)配置交换机S1 Switch>enab…...

海山数据库(He3DB)原理剖析:浅析Doris跨源分析能力
Doris湖仓分析背景: Doris多数据源功能演进 Doris的生态近年来围绕湖仓分析做了较多工作,Doris一直在积极拓宽大数据生态的OLAP分析市场,Doris2.0之后为了满足湖仓分析场景,围绕multi-catalog、数据缓存、容错、pipeline资源管理…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
