算法-数论-蓝桥杯
算法-数论
1、最大公约数
def gcd(a,b):if b == 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b != 0:cur = aa = bb = cur%bpassreturn a
欧几里得算法
a可以表示成a = kb + r(a,b,k,r皆为正整数,且r不为0)
假设d是a,b的一个公约数,记作d|a,d|b,即a和b都可以被d整除。
而r = a - kb,两边同时除以d,r/d=a/d-kb/d,由等式右边可知m=r/d为整数,因此d|r
因此d也是b,a mod b的公约数。
因(a,b)和(b,a mod b)的公约数相等,则其最大公约数也相等,得证。
例题:
1、蓝桥杯2019年第十届省赛真题-等差数列 - C语言网 (dotcpp.com)
import math
n=int(input())
arr=list(map(int,input().split()))if arr[0] > arr[1]:max_ = arr[0]min_ = arr[1]
else:max_ = arr[1]min_ = arr[0]
sub = max_ -min_
for i in range(2, n):sub = math.gcd(sub, abs(arr[i]-arr[i-1]))min_ = min(min_, arr[i])max_ = max(max_, arr[i])
if max_ == min_ : print(n)
else:print((max_ - min_) // sub + 1)
2、1223. 最大比例 - AcWing题库
辗转相减法
n = int(input())
arr = list(map(int, input().split()))
arr.sort()def gcd(a,b):if b == 0:return areturn gcd(b, a%b)
top, bot = 0,0
def gcd_sub(a, b):if a < b:a,b = b,aif b==1:return areturn gcd_sub(b, a//b)
i = 1
while i < n:if arr[i] != arr[0]:gcd_ = gcd(arr[i], arr[0])top = arr[i]//gcd_bot = arr[0]//gcd_breaki += 1
if i == n:print(1)
else:for i in range(i, n):gcd_ = gcd(arr[i], arr[0])a = arr[i]//gcd_b = arr[0]//gcd_top = gcd_sub(a, top)bot = gcd_sub(b, bot)print(f'{top}/{bot}')1.1 扩展欧几里得定律
def ext_euclid(a, b): if b == 0: return 1, 0, a else: x, y, q = ext_euclid(b, a % b) # q = gcd(a, b) = gcd(b, a%b) x, y = y, (x - (a // b) * y) return x, y, q
扩展欧几里得算法求系数x,y_哔哩哔哩_bilibili

例题:1299. 五指山 - AcWing题库
def olai(a, b):if b == 0:return 1,0,ax, y, gcd = olai(b, a%b)x, y = y, x-(a//b)*yreturn x, y, gcddef funt(n, d, x, y):x1, y1, gcd = olai(n, d)if (y-x)%gcd != 0:print('Impossible')else:d = y1*(y-x)//gcdn //= gcd # ax+by = n; x = x+k*(b/gcd(a,b)); y = y+k*(a/gcd(a,b))print((d%n+n)%n)for _ in range(int(input())):n, d, x, y = map(int, input().split())funt(n, d, x, y)
2、最小公倍数
def funt(a,b):return a*b//gcd(a,b)
最小公倍数 * 最大公约数 == a*b
3、质数筛
def getPrimes(n):is_primes = [True]*(n+1) # 初始化一个布尔数组,表示从2到n的所有数都是质数primes = [] # 存储质数for i in range(2, int(n**(1/2))+1):if is_primes[i]:primes.append(i)# 将当前质数的所有倍数标记为非质数for j in range(i*i, n+1, i): is_primes[j] = False# 后面的质数的倍数一定会超for i in range(int(n**(1/2))+1, n+1):if is_primes[i]:primes.append(i)return primes
4、区间质数筛
import mathdef simple_sieve(limit):primes = []sieve = [True] * (limit + 1)# 0和1不是质数,所以标记为Falsesieve[0] = sieve[1] = False# 从2到根号limit遍历数字for num in range(2, int(math.sqrt(limit)) + 1):if sieve[num]:primes.append(num)for multiple in range(num * num, limit + 1, num):sieve[multiple] = Falsefor num in range(int(math.sqrt(limit)) + 1, limit + 1):if sieve[num]:primes.append(num)return primesdef segmented_sieve(start, end):# 计算质数的上限limit = int(math.sqrt(end)) + 1primes = simple_sieve(limit)primes_count = len(primes)# 创建一个布尔数组,用于标记区间内的数字是否为质数,初始化为Truesieve = [True] * (end - start + 1)# 对于每一个小于等于根号end的质数for i in range(primes_count):# 计算刚好大于等于start的primes[i]的数base = max(primes[i]*primes[i], ((start + primes[i] - 1) // primes[i]) * primes[i])# 将当前质数的倍数标记为非质数for j in range(base, end + 1, primes[i]):sieve[j - start] = False# 生成区间内的质数列表segmented_primes = [start + i for i in range(end - start + 1) if sieve[i]]return segmented_primesstart = 10
end = 50
segmented_sieve(start, end)
5、欧拉函数
def funt(n):count = np = 2while p*p <= n:# 找到质因子if n % p == 0:while n % p == 0:n //= pcount -= count//p # n*(1-p)p += 1if n > 1:count -= count//nreturn count
funt(20)
欧拉函数公式证明_哔哩哔哩_bilibili
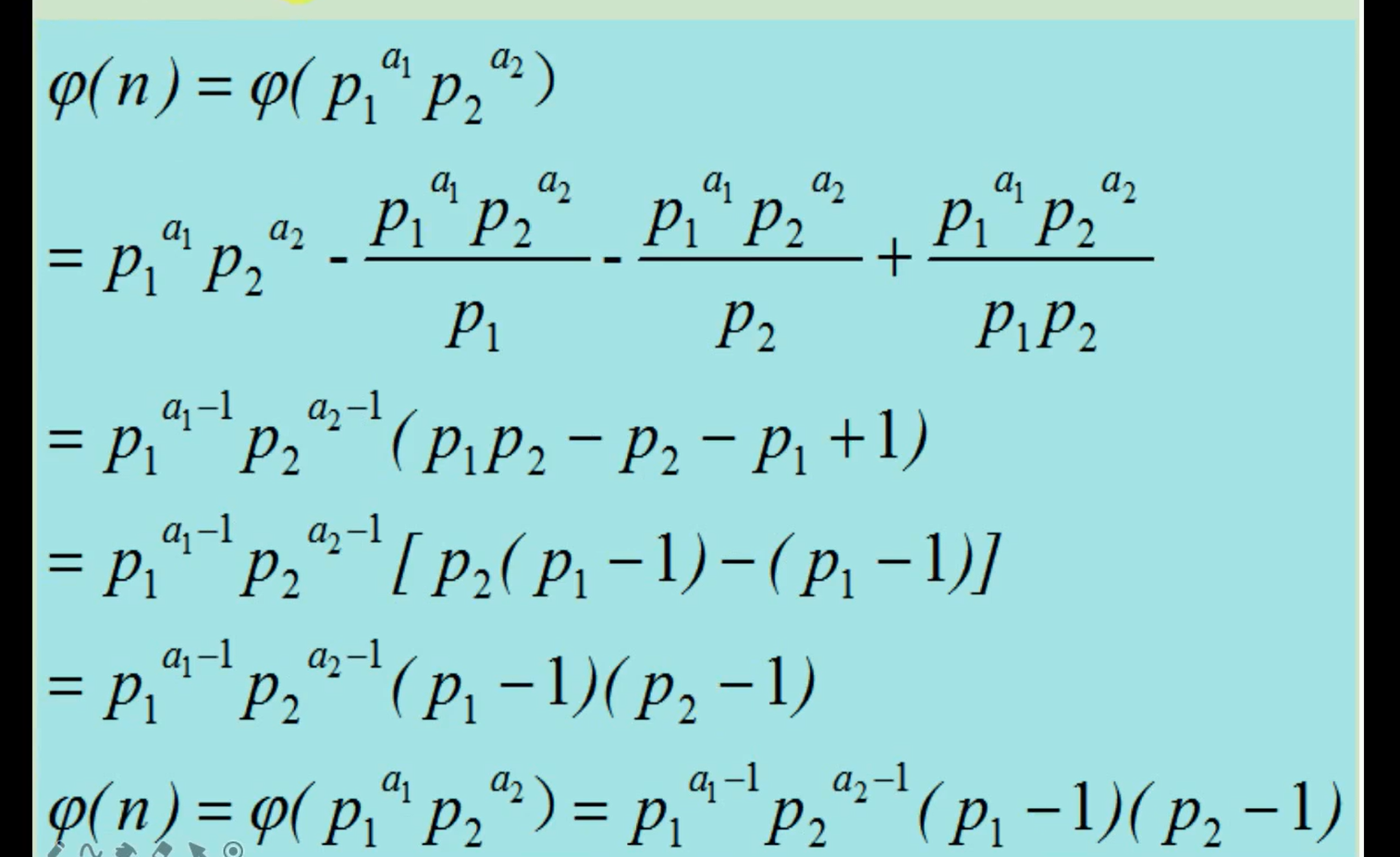
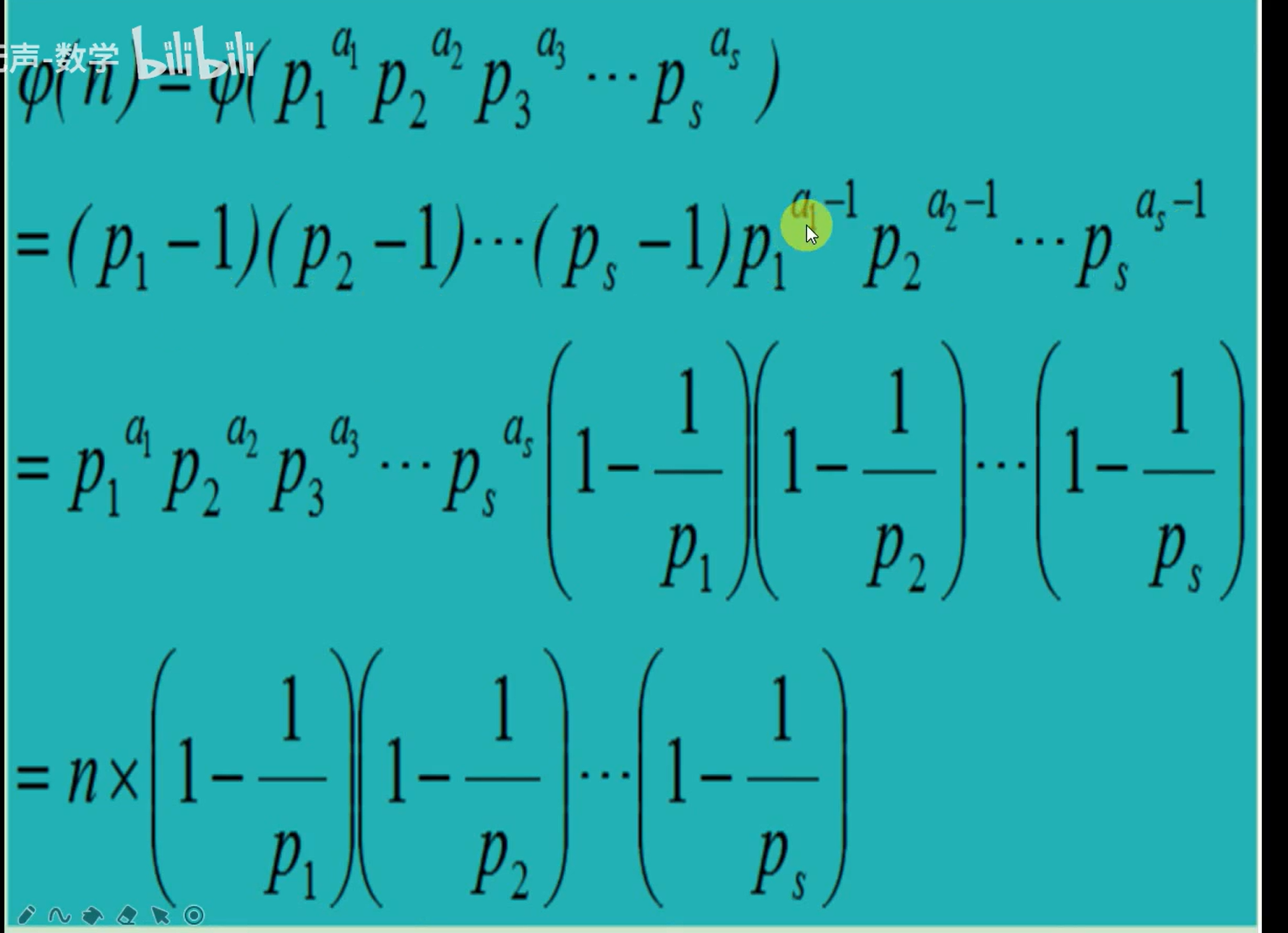
6、计算质因子个数
def funt(n):count = 0p = 2while p * p <= n:if n % p == 0:count += 1while n % p == 0:n //= pp += 1if n > 1:count += 1return count
funt(12)
7、计算所有约数个数
约数,又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数,就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。
def funt(n):count = 1p = 2while p*p <= n:cnt = 0while n%p == 0:cnt += 1n //= pcount *= (cnt+1)if n>1:count *= 2return count
funt(12)
如12:12可以写成2 ** 2 *3,所以 对于2的选择有3种,幂为0、1、2;3的选择有两种,幂为0、1.
相乘即为约数和
8、计算所有约数和
def funt(n):cnt = 0p = 1while p*p <= n:# 一次算两个约数if n%p == 0:cnt += p# 平方就只用算一次if p*p != n:cnt += n//pp += 1return cnt
funt(12)
例题
1295. X的因子链 - AcWing题库
# 方法一 动规
def funt(n):primes = [n]p = 2while p*p <= n:if n%p == 0:primes.append(p)if p*p != n:primes.append(n//p)p += 1if n>1 and n != primes[0]:primes.append(n)primes.sort()dp = [[1]*len(primes) for _ in range(2)]for i in range(1, len(primes)):max_ = cnt = 0for j in range(i):if primes[i] % primes[j] == 0:if dp[0][j] > max_:cnt = dp[1][j]max_ = dp[0][j]elif dp[0][j] == max_:cnt += dp[1][j]dp[0][i],dp[1][i] = max_+1, cnt if cnt else 1print(dp[0][-1], dp[1][-1])
while True:try:n = int(input())funt(n)except EOFError:break# 数学!!! https://www.acwing.com/solution/content/97535/ 具体请看题解,我实在不知道怎么表达o(´^`)o
def A(a, b):cnt = 1while b > 0:cnt *= aa -= 1b -= 1return cntdef funt(n):cnt = []p = 2while p*p <= n:if n%p == 0:cnt_ = 0while n%p == 0:cnt_ += 1n //= pcnt.append(cnt_)p += 1if n>1:cnt.append(1)sum_ = sum(cnt)a = 1for i in cnt:if i > 1:a *= A(i,i)times = A(sum_, sum_)//aprint(sum_, times)
while True:try:n = int(input())funt(n)except EOFError:break9、快速幂
# n为负数则最终结果返回 1/pow(x,-n)
def pow(x, n):if n < 2:return x**nret = pow(x, n//2)if n%2:return ret*ret*xreturn ret*ret
pow(2, 10)
1:
a *= A(i,i)
times = A(sum_, sum_)//a
print(sum_, times)
while True:
try:
n = int(input())
funt(n)
except EOFError:
break
## 9、快速幂```Python
# n为负数则最终结果返回 1/pow(x,-n)
def pow(x, n):if n < 2:return x**nret = pow(x, n//2)if n%2:return ret*ret*xreturn ret*ret
pow(2, 10)
相关文章:
算法-数论-蓝桥杯
算法-数论 1、最大公约数 def gcd(a,b):if b 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b ! 0:cur aa bb cur%bpassreturn a欧几里得算法 a可以表示成a kb r(a,b,k,…...

222.完全二叉树节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最…...

C++中的string类操作详解
引言 针对C中的string,本文主要讲解如何对其进行插入、删除、查找、比较、截断、分割以及与数字之间的相互转换等。 字符串插入 1. append方法 std::string str "hello"; str.append(7, w); // 在末尾添加7个字符w str.append("wwwwwww");…...

Java绘图坐标体系
一、介绍 下图说明了Java坐标系。坐标原点位于左上角,以像素为单位。在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐…...
【MATLAB源码-第38期】基于OFDM的块状导频和梳状导频误码率性能对比,以及LS/LMMSE两种信道估计方法以及不同调制方式对比。
操作环境: MATLAB 2022a 1、算法描述 块状导频和梳状导频都是用于无线通信系统中信道估计的方法。 块状导频: 定义: 在频域上,块状导频是连续放置的一组导频符号。这意味着所有的导频符号都集中在一个短的时间段内发送。 优点…...
javaWeb车辆管理系统设计与实现
摘 要 随着经济的日益增长,车辆作为最重要的交通工具,在企事业单位中得以普及,单位的车辆数目已经远远不止简单的几辆,与此同时就产生了车辆资源的合理分配使用问题。 企业车辆管理系统运用现代化的计算机管理手段,不但可以对车辆的使用进行合理的管理,…...
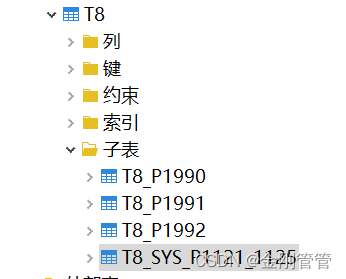
【DM8】间隔分区
是范围分区的一个扩展 如果使用了间隔函数做分区,在数据插入的时候,如果没有合适的分区,数据库会自动创建一个新的分区。 –year往后推两年 SELECT SYSDATE numtoyminterval(2,‘YEAR’); –month往后推两年 SELECT SYSDATE numtoyminterv…...

0基础如何进入IT行业?
目录 0基础如何进入IT行业? 一、学习路径 二、技能培养 三、实践经验 0基础如何进入IT行业? 对于没有任何相关背景知识的人来说,成功进入IT行业可能看起来是一个遥不可及的目标。然而,只要有正确的方法和坚持不懈的努力&#…...
C#将Console写至文件,且文件固定最大长度
参考文章 将C#的Console.Write同步到控制台和log文件输出 业务需求 在生产环境中,控制台窗口不便展示出来。 为了在生产环境中,完整记录控制台应用的输出,选择将其输出到文件中。 但是,一次性存储所有输出的话,文件会…...

《CSS 知识点》仅在文本有省略号时添加 tip 信息
html <div ref"btns" class"btns"><div class"btn" >这是一段很短的文本.</div><div class"btn" >这是一段很短的文本.</div><div class"btn" >这是一段很长的文本.有省略号和tip.<…...

彩虹聚合DNS管理系统v1.0全新发布
聚合DNS管理系统(https://github.com/netcccyun/dnsmgr)可以实现在一个网站内管理多个平台的域名解析,目前已支持的域名平台有:阿里云、腾讯云、华为云、西部数码、CloudFlare。本系统支持多用户,每个用户可分配不同的…...

3.10 Python数据类型转换
Python类型转换,Python数据类型转换函数大全 虽然 Python 是弱类型编程语言,不需要像Java或 C 语言那样还要在使用变量前声明变量的类型,但在一些特定场景中,仍然需要用到类型转换。 比如说,我们想通过使用 print() …...

Kotlin基础学习
Kotlin基础学习主要涵盖安装Kotlin编译器、了解基础语法、学习变量声明、类型推断、函数定义以及控制结构等方面。以下是一个简要的Kotlin基础学习指南: 一、安装Kotlin 首先,你需要从JetBrains的官方网站下载并安装Kotlin编译器。同时,你也…...
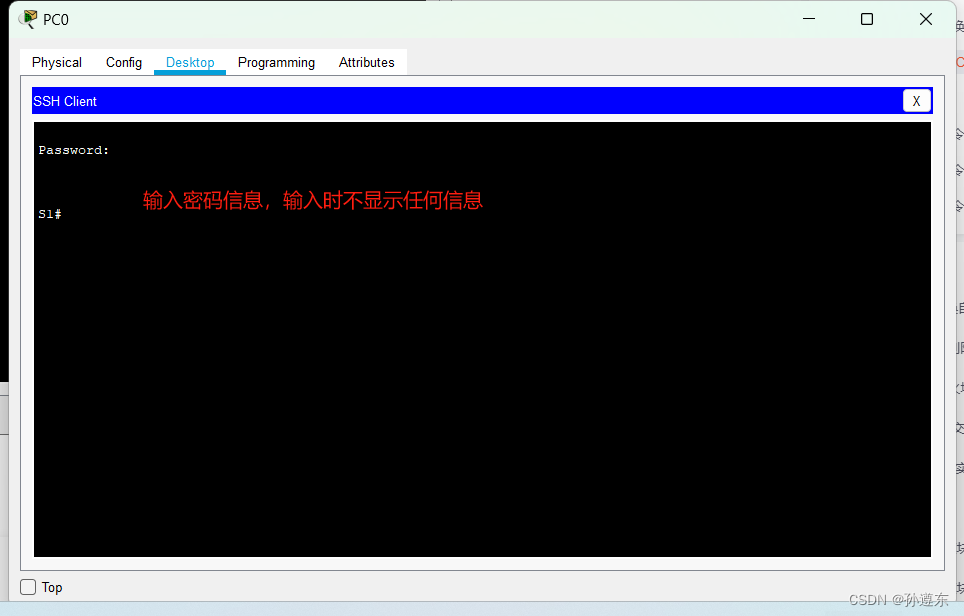
配置交换机 SSH 管理和端口安全——实验1:配置交换机基本安全和 SSH管理
实验目的 通过本实验可以掌握: 交换机基本安全配置。SSH 的工作原理和 SSH服务端和客户端的配置。 实验拓扑 交换机基本安全和 SSH管理实验拓扑如图所示。 交换机基本安全和 SSH管理实验拓扑 实验步骤 (1)配置交换机S1 Switch>enab…...

海山数据库(He3DB)原理剖析:浅析Doris跨源分析能力
Doris湖仓分析背景: Doris多数据源功能演进 Doris的生态近年来围绕湖仓分析做了较多工作,Doris一直在积极拓宽大数据生态的OLAP分析市场,Doris2.0之后为了满足湖仓分析场景,围绕multi-catalog、数据缓存、容错、pipeline资源管理…...

第十三届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组 题解
VP比赛链接 : 数据加载中... - 蓝桥云课 1 . 九进制 转 十进制 直接模拟就好了 #include <iostream> using namespace std; int main() {// 请在此输入您的代码int x 22*92*81*9;cout << x << endl ;return 0; } 2 . 顺子日期 枚举出每个情况即可 : …...

20240324-1-集成学习面试题EnsembleLearning
集成学习面试题 1. 什么是集成学习算法? 集成学习算法是一种优化手段或者策略,将多个较弱的模型集成模型组,一般的弱分类器可以是决策树,SVM,KNN等构成。其中的模型可以单独进行训练,并且它们的预测能以某…...

默克尔(Merkle)树 - 原理及用途
默克尔(Merkle)树的原理以及用途 引言 在当今数字化时代,确保数据的完整性是至关重要的。默克尔树作为一种高效的数据结构,被广泛应用于网络安全、分布式系统以及加密货币等领域,用于验证大量数据的完整性和一致性 数…...

设计模式:迭代器模式
迭代器模式的示例可以涵盖各种数据结构的遍历,包括数组、列表、树、图等。下面是一些不同场景下迭代器模式的示例及其代码实现。 示例 1: 数组遍历 使用迭代器模式遍历数组。 // 迭代器接口 interface Iterator<T> {boolean hasNext();T next(); }// 数组迭…...

Navicat Premium 16常用快捷键
打开一个新的查询窗口: Ctrl Q 关闭当前窗口: Ctrl W 运行当前窗口的SQL语句: Ctrl R 运行选中的SQL语句: Ctrl Shift R 注释选中的SQL语句: Ctrl / 取消注释SQL: Ctrl Shift / 保存连接&…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
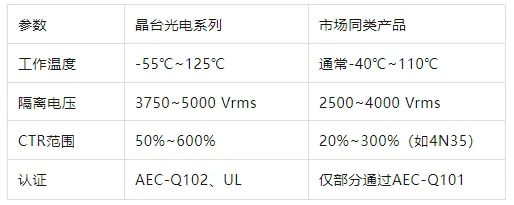
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
