20240324-1-集成学习面试题EnsembleLearning
集成学习面试题

1. 什么是集成学习算法?
集成学习算法是一种优化手段或者策略,将多个较弱的模型集成模型组,一般的弱分类器可以是决策树,SVM,KNN等构成。其中的模型可以单独进行训练,并且它们的预测能以某种方式结合起来去做出一个总体预测。
2. 集成学习主要有哪几种框架?
集成学习从集成思想的架构分为Bagging,Boosting,Stacking三种。
3. 简单介绍一下bagging,常用bagging算法有哪些?
-
Bagging
- 多次采样,训练多个分类器,集体投票,旨在减小方差,
-
基于数据随机重抽样的分类器构建方法。从训练集中进行子抽样组成每个基模型所需要的子训练集,对所有基模型预测的结果进行综合产生最终的预测结果。
-
算法流程:
- 输入为样本集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) … ( x m , y m ) D={(x_1,y_1),(x_2,y_2) \dots (x_m,y_m)} D=(x1,y1),(x2,y2)…(xm,ym),弱学习器算法,弱分类器迭代次数 T T T。
- 输出为最终的强分类器 f ( x ) f(x) f(x)
-
对于 t = 1 , 2 … T t=1,2 \dots T t=1,2…T
- 对训练集进行第t次随机采样,共采集 T T T次,得到包含 T T T个样本的采样集 D t D_t Dt
- 用采样集 D t D_t Dt训练第 t t t个弱学习器 G t ( x ) G_t(x) Gt(x)
-
如果是分类算法预测,则 T T T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法, T T T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
-
常用bagging算法:随机森林算法
4. 简单介绍一下boosting,常用boosting算法有哪些?
-
Boosting
- 基分类器层层叠加,聚焦分错的样本,旨在减小方差
-
训练过程为阶梯状,基模型按次序进行训练(实现上可以做到并行),基模型的训练集按照某种策略每次都进行一定的转化,每次都是提高前一次分错了的数据集的权值,最后对所有基模型预测的结果进行线性组合产生最终的预测结果。
-
算法流程:
-
给定初始训练数据,由此训练出第一个基学习器;
-
根据基学习器的表现对样本进行调整,在之前学习器做错的样本上投入更多关注;
-
用调整后的样本,训练下一个基学习器;
-
重复上述过程T次,将T个学习器加权结合。
-
-
常用boosting算法:
- Adaboost
- GBDT
- XGBoost
5. boosting思想的数学表达式是什么?
f ( x ) = w 0 + ∑ m = 1 M w m ϕ m ( x ) f(x)=w_{0}+\sum_{m=1}^{M} w_{m} \phi_{m}(x) f(x)=w0+m=1∑Mwmϕm(x)
其中 w w w是权重, ϕ \phi ϕ是弱分类器的集合,可以看出最终就是基函数的线性组合。
6. 简单介绍一下stacking
-
Stacking
- 多次采样,训练多个分类器,将输出作为最后的输入特征
-
将训练好的所有基模型对训练集进行预测,第个 i i i基模型对第 i i i个训练样本的预测值将作为新的训练集中第 i i i个样本的第 i i i个特征值,最后基于新的训练集进行训练。同理,预测的过程也要先经过所有基模型的预测形成新的测试集,最后再对测试集进行预测。
-
stacking常见的使用方式:
- 由k-NN、随机森林和朴素贝叶斯基础分类器组成,它的预测结果由作为元分类器的逻回归组合。
7. 你意识到你的模型受到低偏差和高方差问题的困扰,应该使用哪种算法来解决问题呢?为什么?
低偏差意味着模型的预测值接近实际值。换句话说,该模型有足够的灵活性,以模仿训练数据的分布。貌似很好,但是别忘了,一个灵活的模型没有泛化能力。这意味着,当这个模型用在对一个未曾见过的数据集进行测试的时候,它会令人很失望。
在这种情况下,我们可以使用bagging算法(如随机森林),以解决高方差问题。bagging算法把数据集分成重复随机取样形成的子集。然后,这些样本利用单个学习算法生成一组模型。接着,利用投票(分类)或平均(回归)把模型预测结合在一起。另外,为了应对大方差,我们可以:
- 使用正则化技术,惩罚更高的模型系数,从而降低了模型的复杂性。
- 使用可变重要性图表中的前n个特征。
- 可以用于当一个算法在数据集中的所有变量里很难寻找到有意义信号的时候。
8. 常用的基分类器是什么?
最常用的基分类器是决策树,原因:
- 决策树可以较为方便地将样本的权重整合到训练过程中,而不需要使用过采样的方法来调整样本权重。
- 决策树的表达能力和泛化能力,可以通过调节树的层数来做折中。
- 数据样本的扰动对于决策树的影响较大,因此不同子样本集合生成的决策树基分类器随机性较大,这样的“不稳定学习器”更适合作为基分类器。此外,在决策树节点分裂的时候,随机地选择一个特征子集,从中找出最优分裂属性,很好地引入了随机性。
9. 可否将随机森林中的基分类器,由决策树替换为线性分类器或K-近邻?请解释为什么?
不能:
-
Bagging的主要好处是集成后的分类器的方差,比基分类器的方差小。
-
随机森林属于Bagging类的集成学习,对样本分布较为敏感的分类器更适用于Bagging。
-
线性分类器或者K-近邻都是较为稳定的分类器,本身方差就不大。
-
线性分类器或者K-近邻可能会由于Bagging的采样,导致在训练中更难收敛,增大偏差。
10. GBDT和RF如何计算特征重要性
- RF有两种方法:
- 通过计算Gini系数的减少量VIm=GI−(GIL+GIR)判断特征重要性,越大越重要。
- 对于一颗树,先使用袋外错误率(OOB)样本计算测试误差a,再随机打乱OOB样本中第i个特征(上下打乱特征矩阵第i列的顺序)后计算测试误差b,a与b差距越大特征i越重要。
-
GBDT计算方法:
- 所有回归树中通过特征i分裂后平方损失的减少值的和/回归树数量 得到特征重要性。 在sklearn中,GBDT和RF的特征重要性计算方法是相同的,都是基于单棵树计算每个特征的重要性,探究每个特征在每棵树上做了多少的贡献,再取个平均值。
-
Xgb主要有三种计算方法:
- importance_type=weight(默认值),特征重要性使用特征在所有树中作为划分属性的次数。
- mportance_type=gain,特征重要性使用特征在作为划分属性时loss平均的降低量。
- importance_type=cover,特征重要性使用特征在作为划分属性时对样本的覆盖度。
相关文章:

20240324-1-集成学习面试题EnsembleLearning
集成学习面试题 1. 什么是集成学习算法? 集成学习算法是一种优化手段或者策略,将多个较弱的模型集成模型组,一般的弱分类器可以是决策树,SVM,KNN等构成。其中的模型可以单独进行训练,并且它们的预测能以某…...

默克尔(Merkle)树 - 原理及用途
默克尔(Merkle)树的原理以及用途 引言 在当今数字化时代,确保数据的完整性是至关重要的。默克尔树作为一种高效的数据结构,被广泛应用于网络安全、分布式系统以及加密货币等领域,用于验证大量数据的完整性和一致性 数…...

设计模式:迭代器模式
迭代器模式的示例可以涵盖各种数据结构的遍历,包括数组、列表、树、图等。下面是一些不同场景下迭代器模式的示例及其代码实现。 示例 1: 数组遍历 使用迭代器模式遍历数组。 // 迭代器接口 interface Iterator<T> {boolean hasNext();T next(); }// 数组迭…...

Navicat Premium 16常用快捷键
打开一个新的查询窗口: Ctrl Q 关闭当前窗口: Ctrl W 运行当前窗口的SQL语句: Ctrl R 运行选中的SQL语句: Ctrl Shift R 注释选中的SQL语句: Ctrl / 取消注释SQL: Ctrl Shift / 保存连接&…...

LeetCode笔记——1042.不邻接植花
题目 有 n 个花园,按从 1 到 n 标记。另有数组 paths ,其中 paths[i] [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中,你打算种下四种花之一。 另外,所有花园 最多 有 3 条路径可以进入或离开. 你需要为每个花园…...

Centos7搭建 Skywalking 单机版
介绍 Skywalking是应用性能监控平台,可用于分布式系统,支持微服务、云原生、Docker、Kubernetes 等多种架构场景。 整体架构如图 Agent :在应用中,收集 Trace、Log、Metrics 等监控数据,使用 RPC、RESTful API、Kafk…...

定制您的设备体验:如何更改Android启动动画
“bootanim"通常是指在操作系统启动过程中显示的动画,尤其是在移动设备或某些定制的Linux发行版中较为常见。这个术语并不是一个标准的命令或工具名称,而是通常用来描述"启动动画”(boot animation)的简称。在Android设备中,启动动…...

Docker日常系列
一、如何build双架构(AMDRAM)镜像 (1) 需求描述 当k8s集群的硬件资源为ARMAMD混合架构时,镜像需要同时支持2种架构,如何构建镜像。 (2) 操作 准备工作:需要将代码在不同架构下build为镜像,以下默认我们…...

Midjourney该怎么用?从零基础到落地实践
前言 从注册登录到基本的操作界面,提示词组成后缀介绍,到主流的生成图片的方式,以及最重要的提示词咒语分享,还有一些我的使用心得,希望对大家有帮助! 喜欢的话欢迎关注我,欢迎点赞收藏评论&am…...
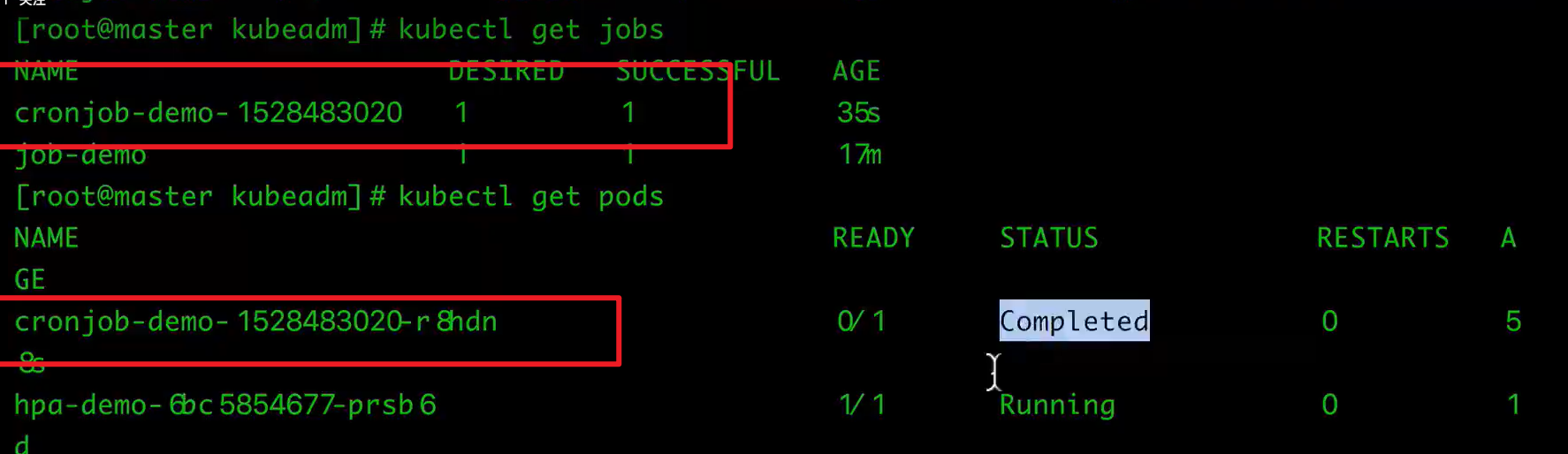
K8S:常用资源对象操作
文章目录 一、使用Replication Controller(RC)、Replica Set(RS) 管理Pod1 Replication Controller(RC)2 Replication Set(RS) 二、Deployment的使用1 创建2 滚动升级3 回滚Deployment三、 Pod 自动扩缩容HPA1 使用kubectl autosc…...

算法刷题应用知识补充--基础算法、数据结构篇
这里写目录标题 枚举结 排序结 模拟结 二分题结 高精度加、乘题结 减题结 除题结 结 位运算(均是拷贝运算,不会影响原数据,这点要注意)&、|、^位运算特性细节知识补充对于n-1的理解异或来实现数字交换找到只出现一次的数据&am…...

ngnix的反向代理是什么?有什么作用?
1、Nginx的反向代理是什么? Nginx的反向代理是一种网络架构模式,其中Nginx服务器作为前端服务器,接收客户端的请求,然后将这些请求转发给后端服务器(例如Java应用程序服务器)。在这个过程中,客…...

Windows程序设计课程作业-1
文章目录 1. 作业内容2. 设计思路分析与难点3. 代码实现3.1 接口定义3.2 工厂类实现3.3 委托和事件3.4 主函数3.5 代码运行结果 4. 代码地址5. 总结&改进思路6. 阅读参考 1. 作业内容 使用 C# 编码(涉及类、接口、委托等关键知识点),实现…...

2024年河北省网络建设与运维-省赛-nginx 和tomcat 服务服务步骤
题目: 5.nginx 和tomcat 服务 任务描述:利用系统自带tomcat,搭建 Tomcat网站。 (1)配置 linux2 为 nginx 服务器,网站目录为/www/nginx,默认文档 index.html 的内容为“HelloNginx”…...
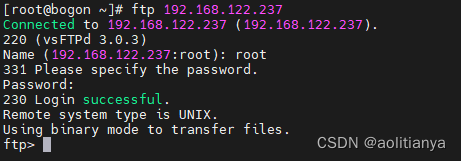
CentOS下部署ftp服务
要在linux部署ftp服务首先需要安装vsftpd服务 yum install vsftpd -y 安装完成后需要启动vsftpd服务 systemctl start vsftpd 为了能够访问ftp的端口,需要在防火墙中开启ftp的端口21,否则在使用ftp连接的时候会报错No route to host. 执行如下命令为f…...
伦敦银几点开盘?为什么交易不了?
近期是西方的假期,伦敦银市场因而休市。很多朋友看到之前伦敦银上涨那么厉害,正摩拳擦掌准备入场大展拳脚,然而现在却吃了一个大瘪:怎么我刚准备好大展拳脚,结果却没有开盘呢?到底伦敦银几点开盘࿱…...

快手开放平台对接内容管理demo
其中包括用户授权,获取accessToken,获取用户信息,自动上传视频,发布视频,视频列表,删除视频等 <?php namespace app\controller;use app\BaseController; use think\Exception; use think\facade\App;…...

2024年32款数据分析工具分五大类总览
数据分析工具在现代商业和科学中扮演着不可或缺的角色,为组织和个人提供了深入洞察和明智决策的能力。这些工具不仅能够处理大规模的数据集,还能通过强大的分析和可视化功能揭示隐藏在数据背后的模式和趋势。数据分析工具软件主要可以划分为以下五个类别…...
WPS的JS宏如何批量实现文字的超链接
表格中需要对文字进行超链接,每个链接指引到不同的地址。例如: 实现如下表格中,文件名称超级链接到对应的文件路径上,点击对应的文件名称,即可打开对应的文件。 序号文件名称文件路径1变更申请与处理表.xls文档\系统…...

0203逆矩阵-矩阵及其运算-线性代数
文章目录 一、逆矩阵的定义、性质和求法二、逆矩阵的初步应用结语 一、逆矩阵的定义、性质和求法 定义7 对于 n n n阶矩阵A,如果有一个 n n n阶矩阵B,使 A B B A E ABBAE ABBAE 则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
