区块链与数字身份:探索Facebook的新尝试
在数字化时代,随着区块链技术的崛起,数字身份成为了一个备受关注的话题。作为全球最大的社交媒体平台之一,Facebook一直在探索如何利用区块链技术来改善数字身份管理和用户数据安全。本文将深入探讨Facebook在这一领域的新尝试,探索其对数字身份的创新和发展。

1. 区块链技术在数字身份管理中的应用
区块链技术以其去中心化、不可篡改、可追溯的特性,为数字身份管理提供了全新的解决方案。Facebook意识到了区块链在用户数据安全和身份验证方面的潜力,并开始探索其在平台上的应用。通过将用户的身份信息和数据存储在区块链上,可以有效防止数据被篡改或盗用,提高用户的数字身份安全性。
2. 数字身份验证与去中心化身份标识
传统的身份验证方式往往需要依赖中心化的机构或第三方服务提供商,存在着数据泄露和信息滥用的风险。而基于区块链的去中心化身份标识系统,则可以让用户拥有自主控制自己身份信息的权利。Facebook正在研究如何利用区块链技术构建去中心化的数字身份验证系统,让用户可以安全地管理和控制自己的身份信息。
3. 数据所有权和隐私保护
随着区块链技术的发展,数字所有权和隐私保护成为了一个重要的议题。Facebook意识到用户对于个人数据的所有权和隐私保护的重要性,开始探索利用区块链技术来实现用户数据的自主控制和隐私保护。通过区块链技术,用户可以拥有自己数据的完全所有权,并且可以选择与其他用户共享或销毁自己的数据,从而实现了数据的真正意义上的隐私保护。
4. 社交身份和数字资产交换
除了数字身份管理外,Facebook还在研究如何利用区块链技术来实现社交身份和数字资产的交换。通过区块链技术,用户可以拥有独一无二的数字身份,同时也可以在平台上进行数字资产的交易和转移。这种基于区块链的社交身份和数字资产交换系统,可以为用户提供更加安全、高效和便捷的社交和交易体验。
5.加密通信保障
IPRockets提供的代理服务采用先进的加密技术,可以确保用户与Facebook平台之间的通信得到安全保障。通过加密通信通道,用户可以更安全地传输敏感数据和个人信息,有效防止信息被窃取或篡改。
6. 挑战与展望
尽管Facebook在区块链和数字身份方面的尝试具有潜力和前景,但也面临着一些挑战和障碍。例如,区块链技术的性能和扩展性问题、法律法规的不确定性、用户接受程度等方面都是需要克服的难题。然而,随着技术的不断进步和社会的不断变革,Facebook对于区块链和数字身份的探索将会继续深入,为数字化社会的发展和进步做出更多贡献。
结语
Facebook正在积极探索利用区块链技术改善数字身份管理和用户数据安全的新途径。通过区块链技术,Facebook希望为用户提供更加安全、高效和便捷的数字身份管理和社交体验。尽管还面临着一些挑战和难题,但Facebook对于区块链和数字身份的未来充满了信心和期待,相信这一领域将会为数字化社会带来更多的创新和进步。
相关文章:

区块链与数字身份:探索Facebook的新尝试
在数字化时代,随着区块链技术的崛起,数字身份成为了一个备受关注的话题。作为全球最大的社交媒体平台之一,Facebook一直在探索如何利用区块链技术来改善数字身份管理和用户数据安全。本文将深入探讨Facebook在这一领域的新尝试,探…...
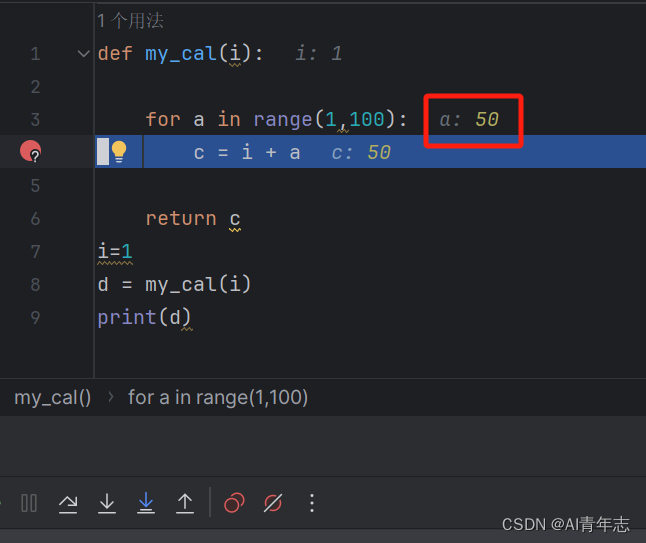
【pycharm】在debug循环时,如何快速debug到指定循环次数
【pycharm】在debug循环时,如何快速debug到指定循环次数 【先赞后看养成习惯】求关注收藏点赞😀 在 PyCharm 中,可以使用条件断点来实现在特定循环次数后停止调试。这可以通过在断点处右键单击,然后选择 “Add Breakpoint” -&g…...

【蓝桥杯每日一题】4.8 公约数
题目来源: 4199. 公约数 - AcWing题库 问题描述: 找到最大整数x,需满足下面两个条件 x x x是 a a a, b b b的公约数 l < x < r l<x<r l<x<r 思路: 找到 a a a, b b b两个数的最大公约数 g c g c d (…...

【MySQL学习】MySQL的慢查询日志和错误日志
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...

# C++之functional库用法整理
C之functional库用法整理 注:整理一些突然学到的C知识,随时mark一下 例如:忘记的关键字用法,新关键字,新数据结构 C 的function库用法整理 C之functional库用法整理一、functional库的内建仿函数1. 存储和调用函数2. 存…...
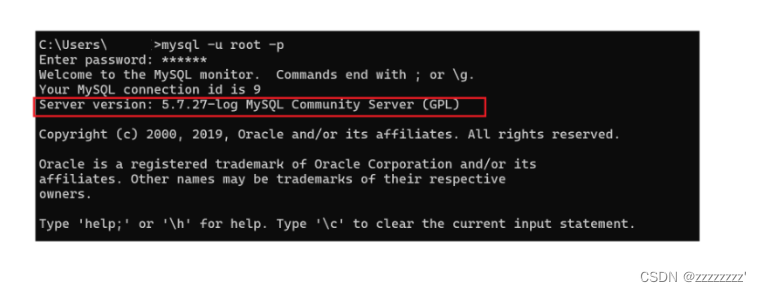
查看MySQL版本的方式
文章目录 一、使用cmd输入命令行查看二、在mysql客户端服务器里查询 一、使用cmd输入命令行查看 1、打开 cmd ,输入命令行: mysql --version 2、还是打开cmd,输入命令行:mysql -V (注意了,此时的V是个大写的V) 二、…...

k8s_入门_命令详解
命令详解 kubectl是官方的CLI命令行工具,用于与 apiserver进行通信,将用户在命令行输入的命令,组织并转化为 apiserver能识别的信息,进而实现管理k8s各种资源的一种有效途径 1. 帮助 2. 查看版本信息 3. 查看资源对象等 查看No…...

腾讯、阿里、字节….等大厂都更喜欢什么样的简历?
我985毕业,为什么筛选简历时输给了一个普通一本? 我投了20份简历,为什么没有一个大厂回我? 每次HR收到简历就没下文了,是我的简历有问题吗? 诚然,在求职时,简历往往就是我们给予H…...

OpenHarmony实战:帆移植案例(中)
OpenHarmony实战:帆移植案例(上) Audio服务介绍 服务节点 基于ADM框架的audio驱动对HDI层提供三个服务hdf_audio_render、hdf_audio_capture、hdf_audio_control。 开发板audio驱动服务节点如下: console:/dev # ls -al hdf_au…...

武汉星起航:创始人张振邦智慧领航,孵化伙伴共绘跨境新蓝图!
在风起云涌的跨境电商行业中,武汉星起航电子商务有限公司如同一颗璀璨的明星,引领着众多创业者迈向成功的彼岸。而这一切的背后,都离不开公司创始人张振邦先生的卓越领导与深厚经验。他凭借着在电子商务行业多年的深耕与积累,为武…...

上下收缩、折叠面板
效果: 上下收缩、折叠面板,类似QQ好友列表那种。原理就是在一个布局中,通过button来实现一个独立widget的visible/disable 实现: 1.分组按钮 #ifndef EXPANDPANEL_H #define EXPANDPANEL_H#include <QWidget>class…...

XC7A35T-2FGG484 嵌入式FPGA现场可编程门阵列 Xilinx
XC7A35T-2FGG484 是一款由Xilinx(赛灵思)制造的FPGA(现场可编程门阵列)芯片 以下是XC7A35T-2FGG484 的主要参数: 1. 系列:Artix-7 2. 逻辑单元数量:33280个 3. 工艺技术:28nm 4. …...

淘宝订单API接口:电商业务自动化的新选择
淘宝订单API接口在电商业务自动化中扮演了至关重要的角色。首先,通过API接口,商家可以自动化地查询、创建、修改和删除订单,极大地提高了订单处理效率,减少了人工操作,降低了错误率。其次,商家可以实时获取…...

识典百科词条创建技巧,教你如何轻松创建热门识典百科词条!
网络已经成为人们获取知识和信息的主要途径。在这样一个背景下,识典百科作为一个综合性的网络百科全书,在为读者们提供各种知识的同时,也给广大用户提供了一个创建、编辑和分享知识的平台。如何在识典百科上创建一个高质量的词条,…...

iOS 开发中上传 IPA 文件的方法(无需 Mac 电脑)
引言 在 iOS 开发中,将 IPA 文件上传到苹果开发者中心是一个重要的步骤。通常情况下,我们需要使用 Mac 电脑上的 Xcode 或 Application Loader 工具来完成这个任务。然而,如果你没有 Mac 电脑,也没有关系,本文将介绍一…...

2024-04-08 问AI: 介绍一下AI 大神 吴恩达
文心一言 吴恩达(Andrew Ng)是AI领域的一位重要人物,他的贡献和影响力在学术界、工业界以及在线教育领域都极为显著。 吴恩达出生于1976年,是一位华裔美国人,他在斯坦福大学担任计算机科学系和电子工程系的副教授&am…...

Leetcode面试经典150_Q12整数转罗马数字
题目: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...

Docker-compose部署Alertmanager+Dingtalk+Prometheus+Grafana实现钉钉报警
部署监控 version: 3.7services: #dingtalkdingtalk:image: timonwong/prometheus-webhook-dingtalk:latestcontainer_name: dingtalkrestart: alwayscommand:- --config.file/etc/prometheus-webhook-dingtalk/config.ymlvolumes:- /data/monitor/dingtalk/config.yml:/etc/p…...

算法刷题记录 Day40
算法刷题记录 Day40 Date: 2024.04.06 kamma 56. 多重背包 #include<bits/stdc.h> using namespace std;int main(){int n, c;while(cin>>c>>n){vector<int> weights(n, 0);vector<int> values(n, 0);vector<int> knums(n, 0);for(int …...
Android JNI基础
目录 一、JNI简介1.1 什么是JNI1.2 用途1.3 优点 二、初探JNI2.1 新建cpp\cmake2.2 build.gradle配置2.3 java层配置2.4 cmake和c 三、API详解3.1 JNI API3.1.1 数据类型3.1.2 方法 3.2 CMake脚本 四、再探JNI 一、JNI简介 1.1 什么是JNI JNI(Java Native Interfa…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
