武汉星起航:创始人张振邦智慧领航,孵化伙伴共绘跨境新蓝图!
在风起云涌的跨境电商行业中,武汉星起航电子商务有限公司如同一颗璀璨的明星,引领着众多创业者迈向成功的彼岸。而这一切的背后,都离不开公司创始人张振邦先生的卓越领导与深厚经验。他凭借着在电子商务行业多年的深耕与积累,为武汉星起航的发展奠定了坚实的基础。
创始人张振邦先生是一位极具远见的电子商务专家。他早在跨境电商发展的红利期便洞察到了其中的巨大潜力,并果断决定投身于这一领域。凭借着自己丰富的电子商务运营经验,他创立了武汉星起航电子商务有限公司,旨在利用自营亚马逊店铺的丰富经验,帮助那些想要在跨境电商领域大展拳脚的伙伴们实现梦想。

武汉星起航电子商务有限公司在张振邦先生的领导下,迅速成为跨境电商行业的佼佼者。公司不仅专注于自营亚马逊跨境电商业务,还致力于为广大初入行业的创业者提供全方位的孵化服务。张振邦先生深知,跨境电商的成功并非一蹴而就,需要深厚的行业洞察、精准的市场定位和高效的运营策略。因此,他带领团队深入研究亚马逊平台的运营规则,不断优化选品策略,提升店铺曝光率和转化率。同时,他们还积极分享自己的经验和资源,帮助刚起步或未起步的伙伴们快速融入跨境电商市场,实现业务增长与品牌提升。
武汉星起航电子商务有限公司在张振邦先生的带领下,不仅自身在跨境电商领域取得了显著成就,更通过一站式卖家孵化服务,帮助无数创业者实现了跨境电商梦想。他们的成功故事成为了行业内的佳话,激励着更多有志之士投身这一充满机遇与挑战的领域。
张振邦先生的成功并非偶然,而是他多年深耕电子商务行业的必然结果。他用自己的智慧和努力,为武汉星起航电子商务有限公司的发展注入了强大的动力。同时,他也用自己的实际行动,为跨境电商行业的繁荣与发展贡献了自己的力量。
未来,武汉星起航电子商务有限公司将继续在张振邦先生的领导下,深耕跨境电商领域,不断创新和进步。他们将继续发挥自身的专业优势和资源优势,为广大创业者提供更加优质、高效的孵化服务。同时,他们也将积极参与行业交流与合作,推动跨境电商行业的持续繁荣与发展。
相关文章:

武汉星起航:创始人张振邦智慧领航,孵化伙伴共绘跨境新蓝图!
在风起云涌的跨境电商行业中,武汉星起航电子商务有限公司如同一颗璀璨的明星,引领着众多创业者迈向成功的彼岸。而这一切的背后,都离不开公司创始人张振邦先生的卓越领导与深厚经验。他凭借着在电子商务行业多年的深耕与积累,为武…...

上下收缩、折叠面板
效果: 上下收缩、折叠面板,类似QQ好友列表那种。原理就是在一个布局中,通过button来实现一个独立widget的visible/disable 实现: 1.分组按钮 #ifndef EXPANDPANEL_H #define EXPANDPANEL_H#include <QWidget>class…...

XC7A35T-2FGG484 嵌入式FPGA现场可编程门阵列 Xilinx
XC7A35T-2FGG484 是一款由Xilinx(赛灵思)制造的FPGA(现场可编程门阵列)芯片 以下是XC7A35T-2FGG484 的主要参数: 1. 系列:Artix-7 2. 逻辑单元数量:33280个 3. 工艺技术:28nm 4. …...

淘宝订单API接口:电商业务自动化的新选择
淘宝订单API接口在电商业务自动化中扮演了至关重要的角色。首先,通过API接口,商家可以自动化地查询、创建、修改和删除订单,极大地提高了订单处理效率,减少了人工操作,降低了错误率。其次,商家可以实时获取…...

识典百科词条创建技巧,教你如何轻松创建热门识典百科词条!
网络已经成为人们获取知识和信息的主要途径。在这样一个背景下,识典百科作为一个综合性的网络百科全书,在为读者们提供各种知识的同时,也给广大用户提供了一个创建、编辑和分享知识的平台。如何在识典百科上创建一个高质量的词条,…...

iOS 开发中上传 IPA 文件的方法(无需 Mac 电脑)
引言 在 iOS 开发中,将 IPA 文件上传到苹果开发者中心是一个重要的步骤。通常情况下,我们需要使用 Mac 电脑上的 Xcode 或 Application Loader 工具来完成这个任务。然而,如果你没有 Mac 电脑,也没有关系,本文将介绍一…...

2024-04-08 问AI: 介绍一下AI 大神 吴恩达
文心一言 吴恩达(Andrew Ng)是AI领域的一位重要人物,他的贡献和影响力在学术界、工业界以及在线教育领域都极为显著。 吴恩达出生于1976年,是一位华裔美国人,他在斯坦福大学担任计算机科学系和电子工程系的副教授&am…...

Leetcode面试经典150_Q12整数转罗马数字
题目: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...

Docker-compose部署Alertmanager+Dingtalk+Prometheus+Grafana实现钉钉报警
部署监控 version: 3.7services: #dingtalkdingtalk:image: timonwong/prometheus-webhook-dingtalk:latestcontainer_name: dingtalkrestart: alwayscommand:- --config.file/etc/prometheus-webhook-dingtalk/config.ymlvolumes:- /data/monitor/dingtalk/config.yml:/etc/p…...

算法刷题记录 Day40
算法刷题记录 Day40 Date: 2024.04.06 kamma 56. 多重背包 #include<bits/stdc.h> using namespace std;int main(){int n, c;while(cin>>c>>n){vector<int> weights(n, 0);vector<int> values(n, 0);vector<int> knums(n, 0);for(int …...
Android JNI基础
目录 一、JNI简介1.1 什么是JNI1.2 用途1.3 优点 二、初探JNI2.1 新建cpp\cmake2.2 build.gradle配置2.3 java层配置2.4 cmake和c 三、API详解3.1 JNI API3.1.1 数据类型3.1.2 方法 3.2 CMake脚本 四、再探JNI 一、JNI简介 1.1 什么是JNI JNI(Java Native Interfa…...

裙边挡边带是什么
裙边挡边带:了解其功能与应用 在日常生活和工业生产中,我们经常会遇到各种形状和功能的带子。其中,裙边挡边带是一种特殊类型的带子,它具有独特的结构和功能,被广泛应用于各种场合。本文将介绍裙边挡边带的基本概念、…...
chabot项目介绍
项目介绍 整体的目录如下所示: 上述的项目结构中出了model是必须的外,其他的都可以根据训练的代码参数传入进行调整,有些不需要一定存在data train.pkl:对原始训练语料进行tokenize之后的文件,存储一个list对象,list的每条数据表…...
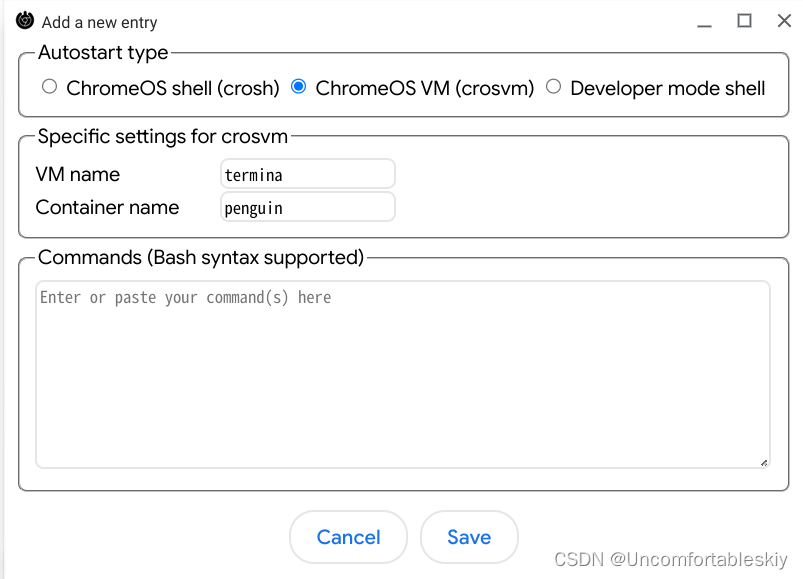
ChromeOS 中自启动 Fcitx5 和托盘 stalonetray
ChromeOS 更新的飞快,旧文章的方法也老是不好用,找遍了也没找到很好的可以开机自启动 Linux VM 和输入法、托盘的方法。 研究了一下(不,是很久),终于找到个丑陋的实现。 方法基于 ChromeOS 123.0.6312.94…...
画图理解JVM相关内容
文章目录 1. JVM视角下,内存划分2. 类内存分布硬核详解1. 获取堆内存参数2. 扫描堆内存,定位实例3. 查看实例所在地址的数据4. 找到实例所指向的类信息的地址5. 查看class信息6. 结论 3. Java的对象创建流程4. 垃圾判别算法4.1 引用计数法4.2 可达性分析…...

Scikit-Learn K均值聚类
Scikit-Learn K均值聚类 1、K均值聚类1.1、K均值聚类及原理1.2、K均值聚类的优缺点1.3、聚类与分类的区别2、Scikit-Learn K均值聚类2.1、Scikit-Learn K均值聚类API2.2、K均值聚类初体验(寻找最佳K)2.3、K均值聚类案例1、K均值聚类 K-均值(K-Means)是一种聚类算法,属于无…...

蓝桥杯 - 受伤的皇后
解题思路: 递归 回溯(n皇后问题的变种) 在 N 皇后问题的解决方案中,我们是从棋盘的顶部向底部逐行放置皇后的,这意味着在任何给定时间,所有未来的行(即当前行之下的所有行)都还没…...

AcWing---乌龟棋---线性dp
312. 乌龟棋 - AcWing题库 思路: 原来没有碰到过类似的题: dp数组为思维:dp[i][j][k][r],分别表示用了i个第一类型卡片,j个第二类型卡片...所到的格子数的最大分数,为啥不用记录乌龟到了哪里呢࿱…...

python代码使用过程中使用快捷键注释时报错
1.代码 2.代码报错 3.代码注释后的结果 4. 原因...

go之web框架gin
介绍 Gin 是一个用 Go (Golang) 编写的 Web 框架。 它具有类似 martini 的 API,性能要好得多,多亏了 httprouter,速度提高了 40 倍。 如果您需要性能和良好的生产力,您一定会喜欢 Gin。 安装 go get -u github.com/gin-gonic/g…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
