Scikit-Learn K均值聚类
Scikit-Learn K均值聚类
- 1、K均值聚类
- 1.1、K均值聚类及原理
- 1.2、K均值聚类的优缺点
- 1.3、聚类与分类的区别
- 2、Scikit-Learn K均值聚类
- 2.1、Scikit-Learn K均值聚类API
- 2.2、K均值聚类初体验(寻找最佳K)
- 2.3、K均值聚类案例
1、K均值聚类
K-均值(K-Means)是一种聚类算法,属于无监督学习。K-Means在机器学习知识结构中的位置如下:

1.1、K均值聚类及原理
聚类(Clustering)是指将一个数据对象集合划分成簇(子集),使得簇内对象彼此相似,簇间对象不相似。通俗来说,就是将数据划分到不同组中
根据算法原理,常用的聚类算法可分为:基于划分的聚类算法K-Means、基于层次的聚类算法HC、基于密度的聚类算法。本文主要介绍K-Means聚类
K-Means算法起源于1967年,由James MacQueen和J.B.Hartigan提出。K-Means中的K指的是类的数量,Means指均值
K-Means算法的基本原理是:根据样本特征的相似度或距离远近,将样本(N个点)划分成若干个类(K个集群),使得每个点都属于离其最近的中心点(均值)对应的类(集群)
其中,相似度通常使用欧几里得距离来度量,用于计算数据点与质心之间的距离(使用平方):
d ( X i , C j ) = ∣ ∣ X i − C j ∣ ∣ 2 d(X_i,C_j)=||X_i-C_j||^2 d(Xi,Cj)=∣∣Xi−Cj∣∣2
其中, X i X_i Xi是数据点, C j C_j Cj是质心
K-Means假设一个样本属于一个类,K-Means的类别是样本的中心(均值);K-Means的损失函数是样本与其所属类的中心之间的距离平方和(SSE):
J = ∑ j = 1 K ∑ i = 1 N j ∣ ∣ X i − C j ∣ ∣ 2 J=\sum_{j=1}^{K}\sum_{i=1}^{N_j}||X_i-C_j||^2 J=
相关文章:

Scikit-Learn K均值聚类
Scikit-Learn K均值聚类 1、K均值聚类1.1、K均值聚类及原理1.2、K均值聚类的优缺点1.3、聚类与分类的区别2、Scikit-Learn K均值聚类2.1、Scikit-Learn K均值聚类API2.2、K均值聚类初体验(寻找最佳K)2.3、K均值聚类案例1、K均值聚类 K-均值(K-Means)是一种聚类算法,属于无…...

蓝桥杯 - 受伤的皇后
解题思路: 递归 回溯(n皇后问题的变种) 在 N 皇后问题的解决方案中,我们是从棋盘的顶部向底部逐行放置皇后的,这意味着在任何给定时间,所有未来的行(即当前行之下的所有行)都还没…...

AcWing---乌龟棋---线性dp
312. 乌龟棋 - AcWing题库 思路: 原来没有碰到过类似的题: dp数组为思维:dp[i][j][k][r],分别表示用了i个第一类型卡片,j个第二类型卡片...所到的格子数的最大分数,为啥不用记录乌龟到了哪里呢࿱…...

python代码使用过程中使用快捷键注释时报错
1.代码 2.代码报错 3.代码注释后的结果 4. 原因...

go之web框架gin
介绍 Gin 是一个用 Go (Golang) 编写的 Web 框架。 它具有类似 martini 的 API,性能要好得多,多亏了 httprouter,速度提高了 40 倍。 如果您需要性能和良好的生产力,您一定会喜欢 Gin。 安装 go get -u github.com/gin-gonic/g…...
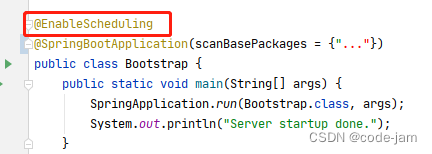
SpringBoot 定时任务实践、定时任务按指定时间执行
Q1. springboot怎样创建定时任务? 很显然,人人都知道,Scheduled(cron ".....") Q2. 如上所示创建了定时任务却未能执行是为什么? 如果你的cron确定没写错的话 cron表达式是否合法,可参考此处,…...

MYSQL数据库故障排除与优化
目录 MySQL 单实例故障排查 MySQL 主从故障排查 MySQL 优化 MySQL 单实例故障排查 故障现象 1 ERROR 2002 (HY000): Cant connect to local MySQL server through socket /data/mysql/mysql.sock (2) 问题分析:以上这种情况一般都…...
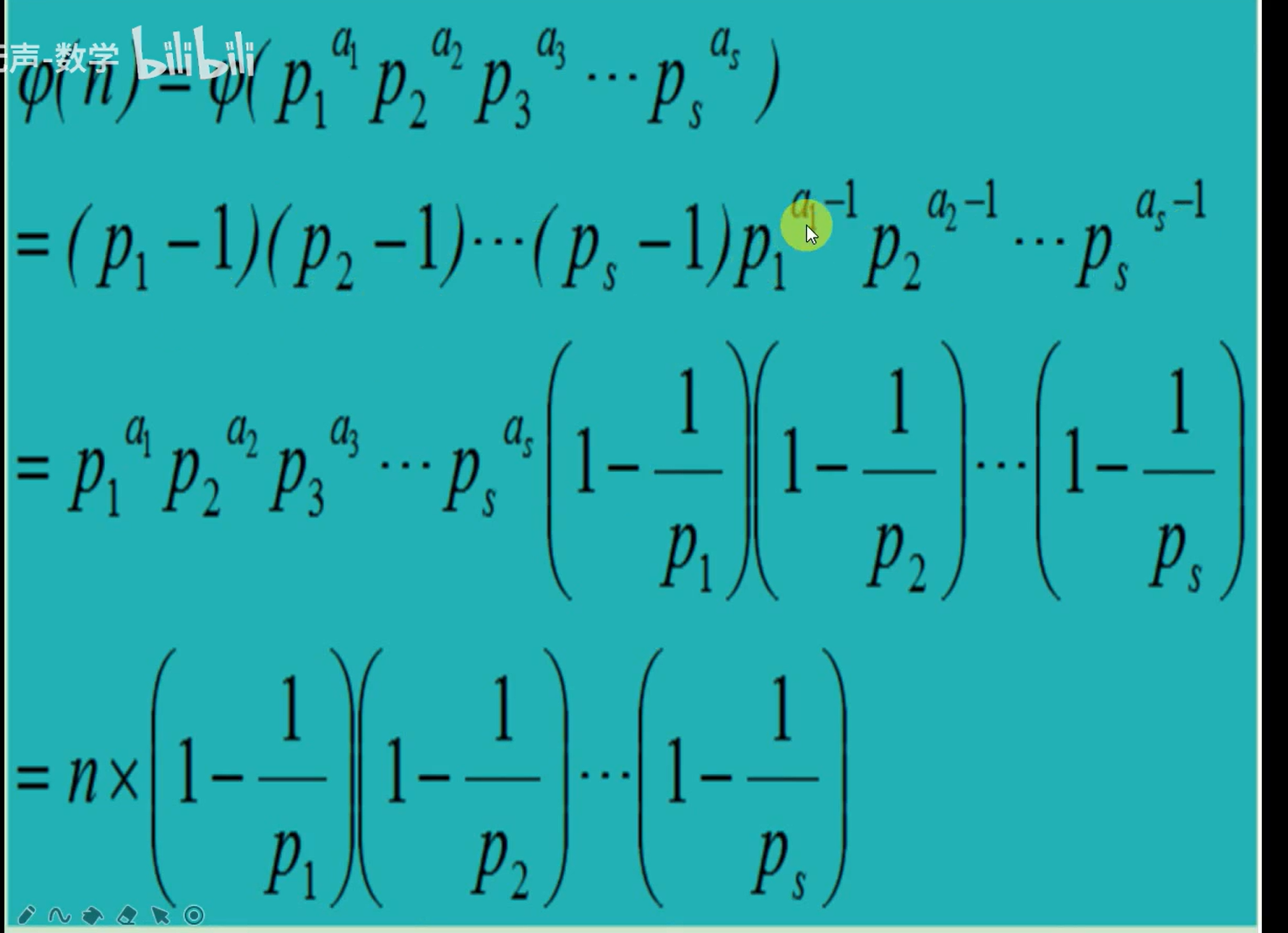
算法-数论-蓝桥杯
算法-数论 1、最大公约数 def gcd(a,b):if b 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b ! 0:cur aa bb cur%bpassreturn a欧几里得算法 a可以表示成a kb r(a,b,k,…...

222.完全二叉树节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最…...

C++中的string类操作详解
引言 针对C中的string,本文主要讲解如何对其进行插入、删除、查找、比较、截断、分割以及与数字之间的相互转换等。 字符串插入 1. append方法 std::string str "hello"; str.append(7, w); // 在末尾添加7个字符w str.append("wwwwwww");…...

Java绘图坐标体系
一、介绍 下图说明了Java坐标系。坐标原点位于左上角,以像素为单位。在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐…...
【MATLAB源码-第38期】基于OFDM的块状导频和梳状导频误码率性能对比,以及LS/LMMSE两种信道估计方法以及不同调制方式对比。
操作环境: MATLAB 2022a 1、算法描述 块状导频和梳状导频都是用于无线通信系统中信道估计的方法。 块状导频: 定义: 在频域上,块状导频是连续放置的一组导频符号。这意味着所有的导频符号都集中在一个短的时间段内发送。 优点…...
javaWeb车辆管理系统设计与实现
摘 要 随着经济的日益增长,车辆作为最重要的交通工具,在企事业单位中得以普及,单位的车辆数目已经远远不止简单的几辆,与此同时就产生了车辆资源的合理分配使用问题。 企业车辆管理系统运用现代化的计算机管理手段,不但可以对车辆的使用进行合理的管理,…...
【DM8】间隔分区
是范围分区的一个扩展 如果使用了间隔函数做分区,在数据插入的时候,如果没有合适的分区,数据库会自动创建一个新的分区。 –year往后推两年 SELECT SYSDATE numtoyminterval(2,‘YEAR’); –month往后推两年 SELECT SYSDATE numtoyminterv…...

0基础如何进入IT行业?
目录 0基础如何进入IT行业? 一、学习路径 二、技能培养 三、实践经验 0基础如何进入IT行业? 对于没有任何相关背景知识的人来说,成功进入IT行业可能看起来是一个遥不可及的目标。然而,只要有正确的方法和坚持不懈的努力&#…...
C#将Console写至文件,且文件固定最大长度
参考文章 将C#的Console.Write同步到控制台和log文件输出 业务需求 在生产环境中,控制台窗口不便展示出来。 为了在生产环境中,完整记录控制台应用的输出,选择将其输出到文件中。 但是,一次性存储所有输出的话,文件会…...

《CSS 知识点》仅在文本有省略号时添加 tip 信息
html <div ref"btns" class"btns"><div class"btn" >这是一段很短的文本.</div><div class"btn" >这是一段很短的文本.</div><div class"btn" >这是一段很长的文本.有省略号和tip.<…...

彩虹聚合DNS管理系统v1.0全新发布
聚合DNS管理系统(https://github.com/netcccyun/dnsmgr)可以实现在一个网站内管理多个平台的域名解析,目前已支持的域名平台有:阿里云、腾讯云、华为云、西部数码、CloudFlare。本系统支持多用户,每个用户可分配不同的…...

3.10 Python数据类型转换
Python类型转换,Python数据类型转换函数大全 虽然 Python 是弱类型编程语言,不需要像Java或 C 语言那样还要在使用变量前声明变量的类型,但在一些特定场景中,仍然需要用到类型转换。 比如说,我们想通过使用 print() …...

Kotlin基础学习
Kotlin基础学习主要涵盖安装Kotlin编译器、了解基础语法、学习变量声明、类型推断、函数定义以及控制结构等方面。以下是一个简要的Kotlin基础学习指南: 一、安装Kotlin 首先,你需要从JetBrains的官方网站下载并安装Kotlin编译器。同时,你也…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
