iOS 开发中上传 IPA 文件的方法(无需 Mac 电脑)
引言
在 iOS 开发中,将 IPA 文件上传到苹果开发者中心是一个重要的步骤。通常情况下,我们需要使用 Mac 电脑上的 Xcode 或 Application Loader 工具来完成这个任务。然而,如果你没有 Mac 电脑,也没有关系,本文将介绍一些无需 Mac 电脑的方法来实现 IPA 文件的上传。

1. 使用在线工具
有一些在线工具可以帮助你将 IPA 文件上传到苹果开发者中心。其中比较常用的工具是appuploder-iPA在线上传小工具。使用这些工具的步骤如下:
- 打开浏览器,并搜索 “iPA在线上传小工具-百度搜索:appuploder”。
- 在appuploder的网页上,提供你的 IPA 文件和开发者账号等必要信息。
- 点击上传按钮,等待上传完成。
这些在线工具通常会将你的 IPA 文件上传到开发者后台,构造文件并完成上传过程。

2. 使用第三方工具
除了在线工具,还有一些第三方工具可以帮助你将 IPA 文件上传到苹果开发者中心。以下是两个常用的工具示例:
- Transporter:
Transporter 是苹果官方提供的一个命令行工具,它可以帮助你将 IPA 文件上传到苹果开发者中心。与 fastlane 不同,Transporter 不需要连接到 Mac 电脑,因此你可以在 PC 或安卓设备上使用它。使用 Transporter 需要一定的技术知识和配置。
综上所述,虽然没有 Mac 电脑,但你仍然有多种方法可以上传 IPA 文件到苹果开发者中心。选择适合自己的方式,并在操作之前仔细阅读相关文档和提示,以避免上传失败或其他问题。
Transporter 工具的使用流程:
- 在你的 PC 或安卓设备上安装和配置 Transporter 工具。
- 连接你的 iOS 设备到电脑。
- 打开终端或命令提示符,并使用 Transporter 命令将 IPA 文件上传到苹果开发者中心。
- 等待上传过程完成。
总结
在本文中,我们介绍了一些无需 Mac 电脑的方法来上传 IPA 文件到苹果开发者中心。你可以使用在线工具如appuploder-iPA在线上传小工具,或者使用第三方工具如fastlane或Transporter。无论你选择哪种方法,请确保在操作之前详细阅读相关文档和提示,以确保上传顺利进行。
参考资料
- appuploder-iPA在线上传小工具
- Transporter文档
相关文章:

iOS 开发中上传 IPA 文件的方法(无需 Mac 电脑)
引言 在 iOS 开发中,将 IPA 文件上传到苹果开发者中心是一个重要的步骤。通常情况下,我们需要使用 Mac 电脑上的 Xcode 或 Application Loader 工具来完成这个任务。然而,如果你没有 Mac 电脑,也没有关系,本文将介绍一…...

2024-04-08 问AI: 介绍一下AI 大神 吴恩达
文心一言 吴恩达(Andrew Ng)是AI领域的一位重要人物,他的贡献和影响力在学术界、工业界以及在线教育领域都极为显著。 吴恩达出生于1976年,是一位华裔美国人,他在斯坦福大学担任计算机科学系和电子工程系的副教授&am…...

Leetcode面试经典150_Q12整数转罗马数字
题目: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...

Docker-compose部署Alertmanager+Dingtalk+Prometheus+Grafana实现钉钉报警
部署监控 version: 3.7services: #dingtalkdingtalk:image: timonwong/prometheus-webhook-dingtalk:latestcontainer_name: dingtalkrestart: alwayscommand:- --config.file/etc/prometheus-webhook-dingtalk/config.ymlvolumes:- /data/monitor/dingtalk/config.yml:/etc/p…...

算法刷题记录 Day40
算法刷题记录 Day40 Date: 2024.04.06 kamma 56. 多重背包 #include<bits/stdc.h> using namespace std;int main(){int n, c;while(cin>>c>>n){vector<int> weights(n, 0);vector<int> values(n, 0);vector<int> knums(n, 0);for(int …...
Android JNI基础
目录 一、JNI简介1.1 什么是JNI1.2 用途1.3 优点 二、初探JNI2.1 新建cpp\cmake2.2 build.gradle配置2.3 java层配置2.4 cmake和c 三、API详解3.1 JNI API3.1.1 数据类型3.1.2 方法 3.2 CMake脚本 四、再探JNI 一、JNI简介 1.1 什么是JNI JNI(Java Native Interfa…...

裙边挡边带是什么
裙边挡边带:了解其功能与应用 在日常生活和工业生产中,我们经常会遇到各种形状和功能的带子。其中,裙边挡边带是一种特殊类型的带子,它具有独特的结构和功能,被广泛应用于各种场合。本文将介绍裙边挡边带的基本概念、…...
chabot项目介绍
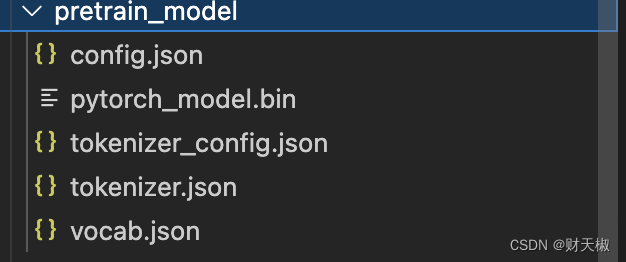
项目介绍 整体的目录如下所示: 上述的项目结构中出了model是必须的外,其他的都可以根据训练的代码参数传入进行调整,有些不需要一定存在data train.pkl:对原始训练语料进行tokenize之后的文件,存储一个list对象,list的每条数据表…...
ChromeOS 中自启动 Fcitx5 和托盘 stalonetray
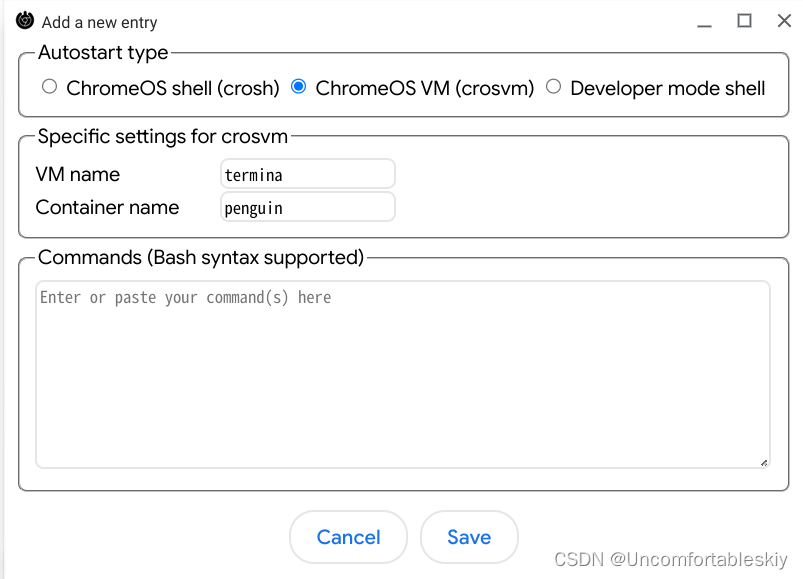
ChromeOS 更新的飞快,旧文章的方法也老是不好用,找遍了也没找到很好的可以开机自启动 Linux VM 和输入法、托盘的方法。 研究了一下(不,是很久),终于找到个丑陋的实现。 方法基于 ChromeOS 123.0.6312.94…...
画图理解JVM相关内容
文章目录 1. JVM视角下,内存划分2. 类内存分布硬核详解1. 获取堆内存参数2. 扫描堆内存,定位实例3. 查看实例所在地址的数据4. 找到实例所指向的类信息的地址5. 查看class信息6. 结论 3. Java的对象创建流程4. 垃圾判别算法4.1 引用计数法4.2 可达性分析…...

Scikit-Learn K均值聚类
Scikit-Learn K均值聚类 1、K均值聚类1.1、K均值聚类及原理1.2、K均值聚类的优缺点1.3、聚类与分类的区别2、Scikit-Learn K均值聚类2.1、Scikit-Learn K均值聚类API2.2、K均值聚类初体验(寻找最佳K)2.3、K均值聚类案例1、K均值聚类 K-均值(K-Means)是一种聚类算法,属于无…...

蓝桥杯 - 受伤的皇后
解题思路: 递归 回溯(n皇后问题的变种) 在 N 皇后问题的解决方案中,我们是从棋盘的顶部向底部逐行放置皇后的,这意味着在任何给定时间,所有未来的行(即当前行之下的所有行)都还没…...

AcWing---乌龟棋---线性dp
312. 乌龟棋 - AcWing题库 思路: 原来没有碰到过类似的题: dp数组为思维:dp[i][j][k][r],分别表示用了i个第一类型卡片,j个第二类型卡片...所到的格子数的最大分数,为啥不用记录乌龟到了哪里呢࿱…...

python代码使用过程中使用快捷键注释时报错
1.代码 2.代码报错 3.代码注释后的结果 4. 原因...

go之web框架gin
介绍 Gin 是一个用 Go (Golang) 编写的 Web 框架。 它具有类似 martini 的 API,性能要好得多,多亏了 httprouter,速度提高了 40 倍。 如果您需要性能和良好的生产力,您一定会喜欢 Gin。 安装 go get -u github.com/gin-gonic/g…...
SpringBoot 定时任务实践、定时任务按指定时间执行
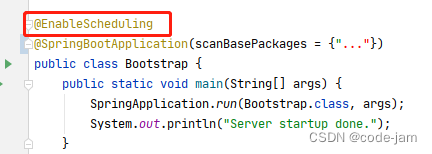
Q1. springboot怎样创建定时任务? 很显然,人人都知道,Scheduled(cron ".....") Q2. 如上所示创建了定时任务却未能执行是为什么? 如果你的cron确定没写错的话 cron表达式是否合法,可参考此处,…...

MYSQL数据库故障排除与优化
目录 MySQL 单实例故障排查 MySQL 主从故障排查 MySQL 优化 MySQL 单实例故障排查 故障现象 1 ERROR 2002 (HY000): Cant connect to local MySQL server through socket /data/mysql/mysql.sock (2) 问题分析:以上这种情况一般都…...
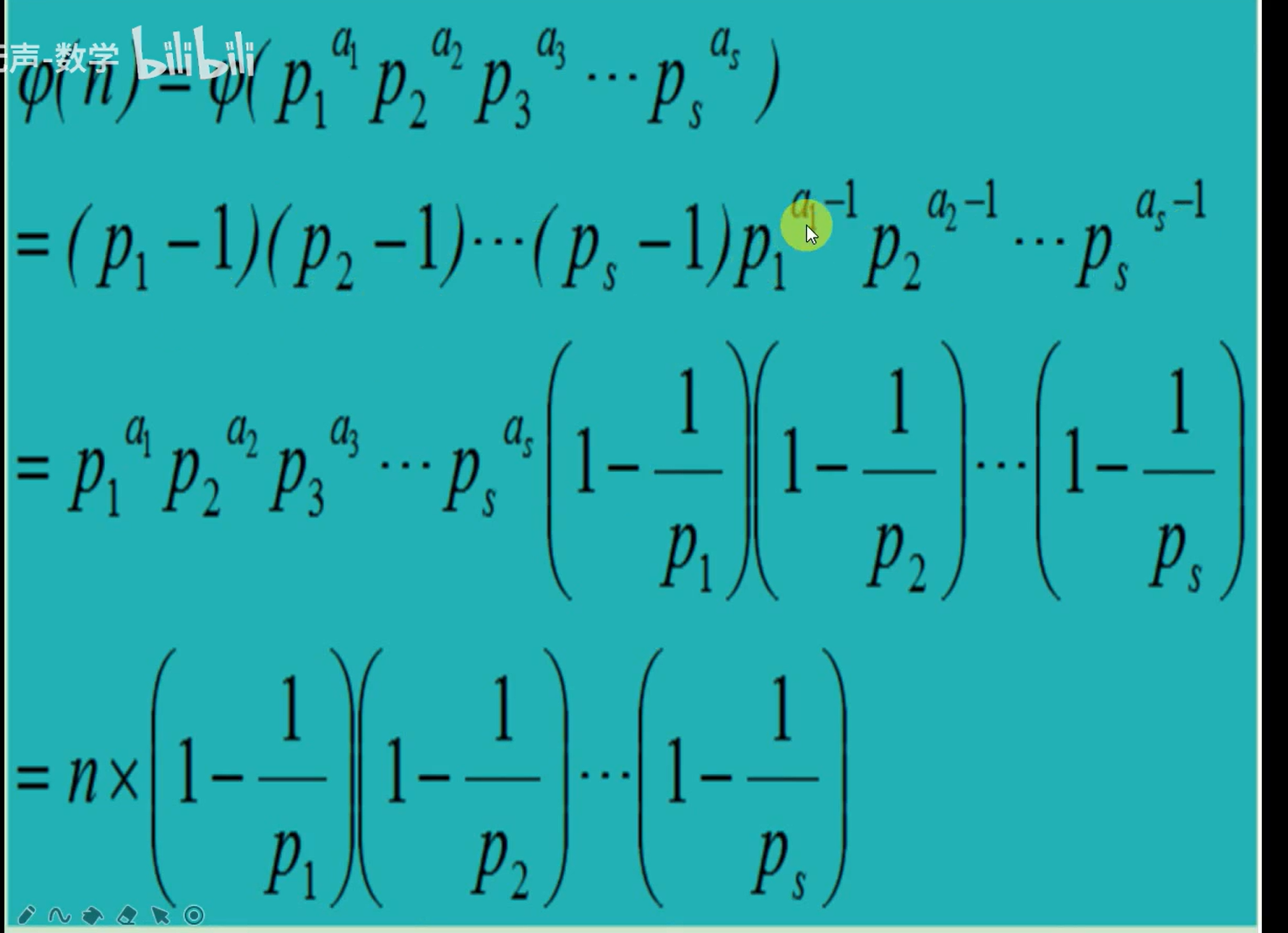
算法-数论-蓝桥杯
算法-数论 1、最大公约数 def gcd(a,b):if b 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b ! 0:cur aa bb cur%bpassreturn a欧几里得算法 a可以表示成a kb r(a,b,k,…...

222.完全二叉树节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最…...

C++中的string类操作详解
引言 针对C中的string,本文主要讲解如何对其进行插入、删除、查找、比较、截断、分割以及与数字之间的相互转换等。 字符串插入 1. append方法 std::string str "hello"; str.append(7, w); // 在末尾添加7个字符w str.append("wwwwwww");…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
