Leetcode面试经典150_Q12整数转罗马数字
题目:
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给你一个整数,将其转为罗马数字。
思路1:无脑取余除(蠢)
Python:
class Solution:def intToRoman(self, num: int) -> str:s=""numList=[1000,500,100,50,10,5,1]temp_1=1dic={1000:"M",500:"D",100:"C",50:"L",10:"X",5:"V",1:"I"}for i in range(7):temp=int(num/numList[i])if i != 6:temp_1=int(num/numList[i+1])if temp==0:continueelif temp_1%9==0 and dic[numList[i+1]]!='V' and dic[numList[i+1]]!='L':num=num%numList[i+1]s=s+dic[numList[i+1]]+dic[numList[i-1]]temp_1=1elif temp%4==0:num=num%numList[i]s=s+dic[numList[i]]+dic[numList[i-1]]else:num=num%numList[i]for j in range(temp):s=s+dic[numList[i]]return s思路2:
根据罗马数字的唯一表示法,为了表示一个给定的整数 num,我们寻找不超过 num 的最大符号值,将 num 减去该符号值,然后继续寻找不超过 num 的最大符号值,将该符号拼接在上一个找到的符号之后,循环直至 num 为 0。
编程时,可以建立一个数值-符号对的列表,按数值从大到小排列。遍历每个数值-符号对,若当前数值 value 不超过 num,则从 num 中不断减去 value,直至 num 小于 value,然后遍历下一个数值-符号对。若遍历中 num 为 0 则跳出循环。
class Solution:VALUE_SYMBOLS = [(1000, "M"),(900, "CM"),(500, "D"),(400, "CD"),(100, "C"),(90, "XC"),(50, "L"),(40, "XL"),(10, "X"),(9, "IX"),(5, "V"),(4, "IV"),(1, "I"),]def intToRoman(self, num: int) -> str:roman = list()for value, symbol in Solution.VALUE_SYMBOLS:while num >= value:num -= valueroman.append(symbol)if num == 0:breakreturn "".join(roman)相关文章:

Leetcode面试经典150_Q12整数转罗马数字
题目: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...

Docker-compose部署Alertmanager+Dingtalk+Prometheus+Grafana实现钉钉报警
部署监控 version: 3.7services: #dingtalkdingtalk:image: timonwong/prometheus-webhook-dingtalk:latestcontainer_name: dingtalkrestart: alwayscommand:- --config.file/etc/prometheus-webhook-dingtalk/config.ymlvolumes:- /data/monitor/dingtalk/config.yml:/etc/p…...

算法刷题记录 Day40
算法刷题记录 Day40 Date: 2024.04.06 kamma 56. 多重背包 #include<bits/stdc.h> using namespace std;int main(){int n, c;while(cin>>c>>n){vector<int> weights(n, 0);vector<int> values(n, 0);vector<int> knums(n, 0);for(int …...
Android JNI基础
目录 一、JNI简介1.1 什么是JNI1.2 用途1.3 优点 二、初探JNI2.1 新建cpp\cmake2.2 build.gradle配置2.3 java层配置2.4 cmake和c 三、API详解3.1 JNI API3.1.1 数据类型3.1.2 方法 3.2 CMake脚本 四、再探JNI 一、JNI简介 1.1 什么是JNI JNI(Java Native Interfa…...

裙边挡边带是什么
裙边挡边带:了解其功能与应用 在日常生活和工业生产中,我们经常会遇到各种形状和功能的带子。其中,裙边挡边带是一种特殊类型的带子,它具有独特的结构和功能,被广泛应用于各种场合。本文将介绍裙边挡边带的基本概念、…...
chabot项目介绍
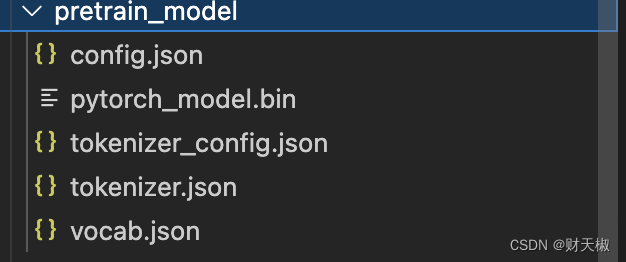
项目介绍 整体的目录如下所示: 上述的项目结构中出了model是必须的外,其他的都可以根据训练的代码参数传入进行调整,有些不需要一定存在data train.pkl:对原始训练语料进行tokenize之后的文件,存储一个list对象,list的每条数据表…...
ChromeOS 中自启动 Fcitx5 和托盘 stalonetray
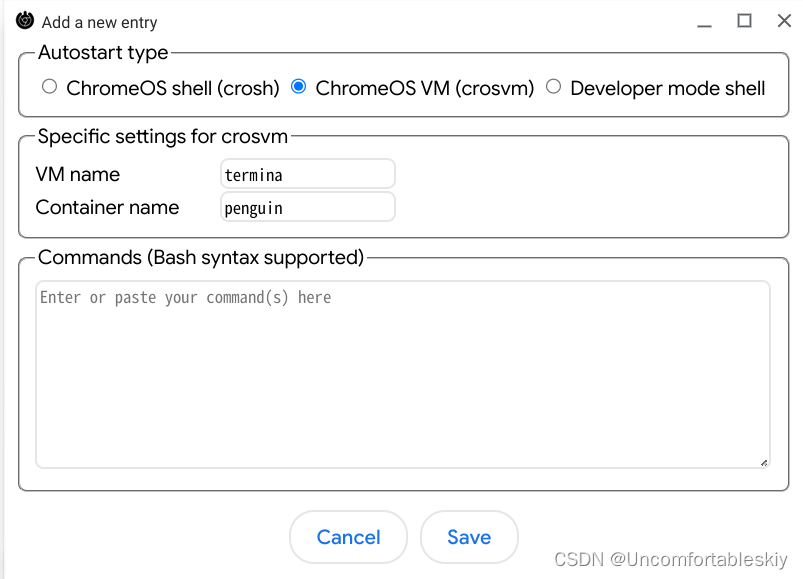
ChromeOS 更新的飞快,旧文章的方法也老是不好用,找遍了也没找到很好的可以开机自启动 Linux VM 和输入法、托盘的方法。 研究了一下(不,是很久),终于找到个丑陋的实现。 方法基于 ChromeOS 123.0.6312.94…...
画图理解JVM相关内容
文章目录 1. JVM视角下,内存划分2. 类内存分布硬核详解1. 获取堆内存参数2. 扫描堆内存,定位实例3. 查看实例所在地址的数据4. 找到实例所指向的类信息的地址5. 查看class信息6. 结论 3. Java的对象创建流程4. 垃圾判别算法4.1 引用计数法4.2 可达性分析…...

Scikit-Learn K均值聚类
Scikit-Learn K均值聚类 1、K均值聚类1.1、K均值聚类及原理1.2、K均值聚类的优缺点1.3、聚类与分类的区别2、Scikit-Learn K均值聚类2.1、Scikit-Learn K均值聚类API2.2、K均值聚类初体验(寻找最佳K)2.3、K均值聚类案例1、K均值聚类 K-均值(K-Means)是一种聚类算法,属于无…...

蓝桥杯 - 受伤的皇后
解题思路: 递归 回溯(n皇后问题的变种) 在 N 皇后问题的解决方案中,我们是从棋盘的顶部向底部逐行放置皇后的,这意味着在任何给定时间,所有未来的行(即当前行之下的所有行)都还没…...

AcWing---乌龟棋---线性dp
312. 乌龟棋 - AcWing题库 思路: 原来没有碰到过类似的题: dp数组为思维:dp[i][j][k][r],分别表示用了i个第一类型卡片,j个第二类型卡片...所到的格子数的最大分数,为啥不用记录乌龟到了哪里呢࿱…...

python代码使用过程中使用快捷键注释时报错
1.代码 2.代码报错 3.代码注释后的结果 4. 原因...

go之web框架gin
介绍 Gin 是一个用 Go (Golang) 编写的 Web 框架。 它具有类似 martini 的 API,性能要好得多,多亏了 httprouter,速度提高了 40 倍。 如果您需要性能和良好的生产力,您一定会喜欢 Gin。 安装 go get -u github.com/gin-gonic/g…...
SpringBoot 定时任务实践、定时任务按指定时间执行
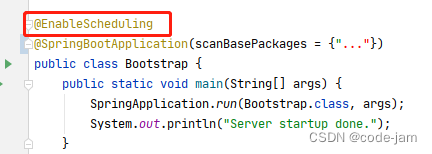
Q1. springboot怎样创建定时任务? 很显然,人人都知道,Scheduled(cron ".....") Q2. 如上所示创建了定时任务却未能执行是为什么? 如果你的cron确定没写错的话 cron表达式是否合法,可参考此处,…...

MYSQL数据库故障排除与优化
目录 MySQL 单实例故障排查 MySQL 主从故障排查 MySQL 优化 MySQL 单实例故障排查 故障现象 1 ERROR 2002 (HY000): Cant connect to local MySQL server through socket /data/mysql/mysql.sock (2) 问题分析:以上这种情况一般都…...
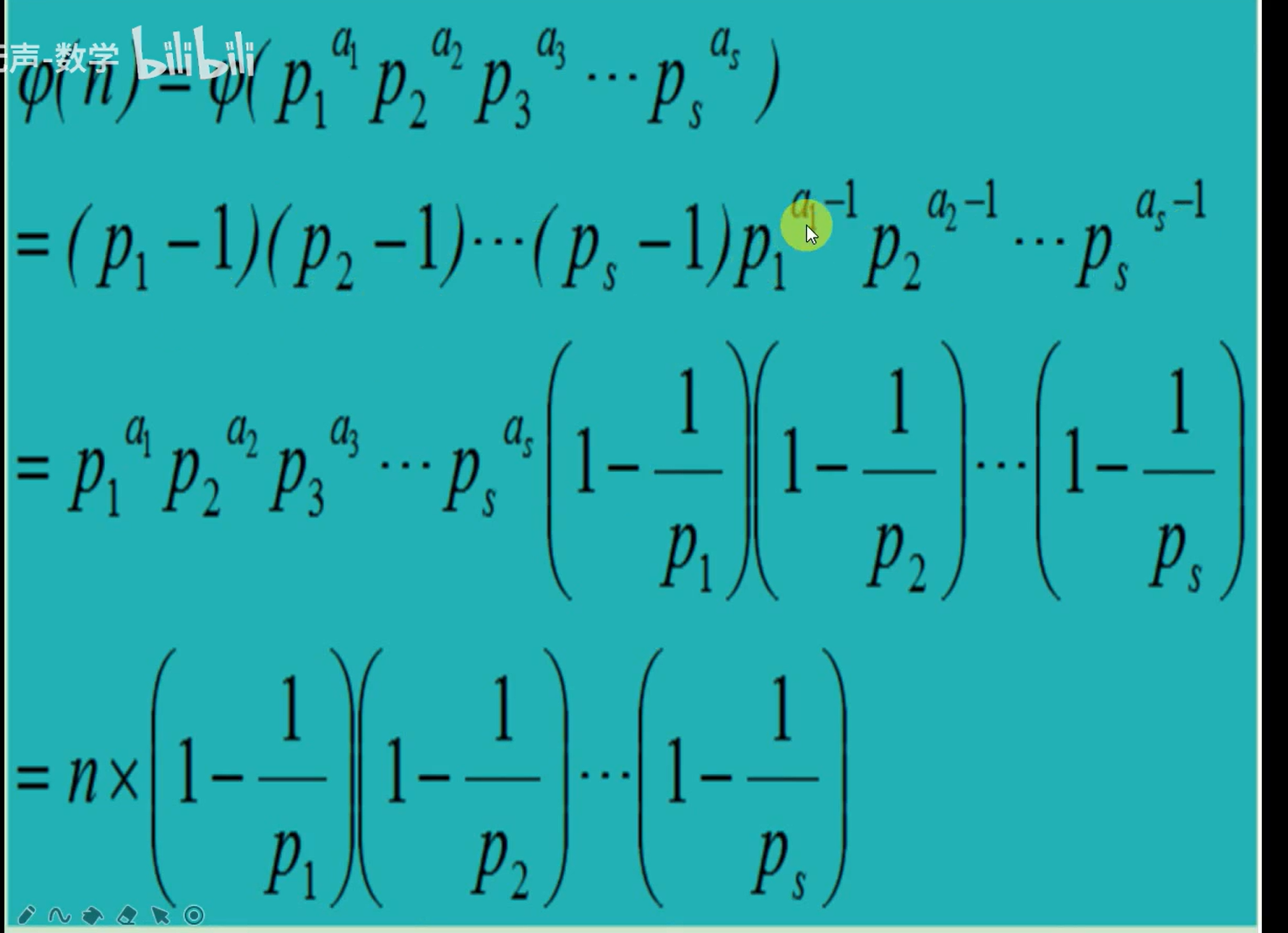
算法-数论-蓝桥杯
算法-数论 1、最大公约数 def gcd(a,b):if b 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b ! 0:cur aa bb cur%bpassreturn a欧几里得算法 a可以表示成a kb r(a,b,k,…...

222.完全二叉树节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最…...

C++中的string类操作详解
引言 针对C中的string,本文主要讲解如何对其进行插入、删除、查找、比较、截断、分割以及与数字之间的相互转换等。 字符串插入 1. append方法 std::string str "hello"; str.append(7, w); // 在末尾添加7个字符w str.append("wwwwwww");…...

Java绘图坐标体系
一、介绍 下图说明了Java坐标系。坐标原点位于左上角,以像素为单位。在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐…...
【MATLAB源码-第38期】基于OFDM的块状导频和梳状导频误码率性能对比,以及LS/LMMSE两种信道估计方法以及不同调制方式对比。
操作环境: MATLAB 2022a 1、算法描述 块状导频和梳状导频都是用于无线通信系统中信道估计的方法。 块状导频: 定义: 在频域上,块状导频是连续放置的一组导频符号。这意味着所有的导频符号都集中在一个短的时间段内发送。 优点…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
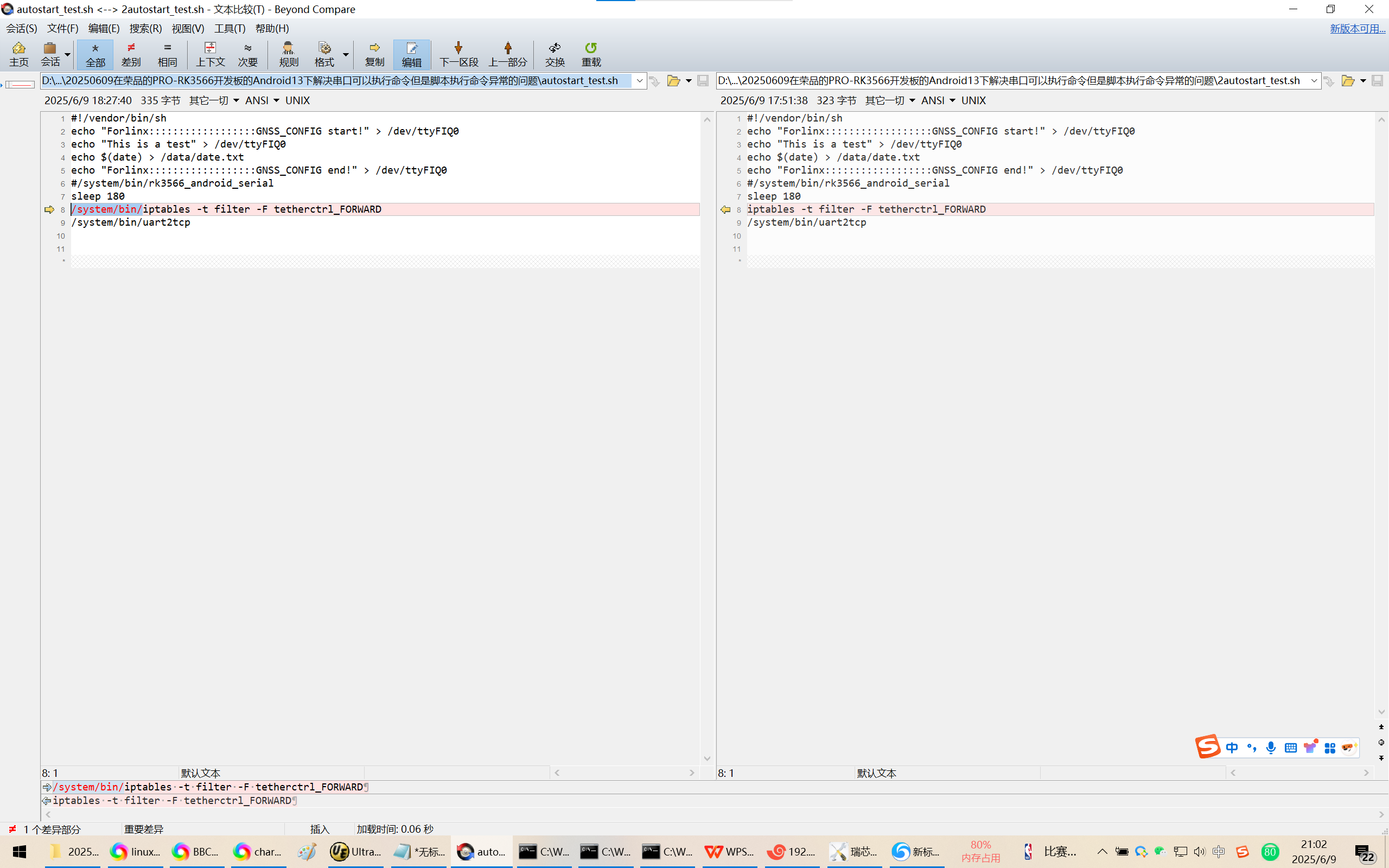
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...

Linux【5】-----编译和烧写Linux系统镜像(RK3568)
参考:讯为 1、文件系统 不同的文件系统组成了:debian、ubuntu、buildroot、qt等系统 每个文件系统的uboot和kernel是一样的 2、源码目录介绍 目录 3、正式编译 编译脚本build.sh 帮助内容如下: Available options: uboot …...
)
GitHub 常见高频问题与解决方案(实用手册)
1.Push 提示权限错误(Permission denied) 问题: Bash Permission denied (publickey) fatal: Could not read from remote repository. 原因: 没有配置 SSH key 或使用了 HTTPS 而没有权限…...
