P5356 [Ynoi2017] 由乃打扑克
我手把手教她打扑克 qwq
综合分析一下2个操作,查找区间第k小的值,感觉可以用主席树,区间修改那没事了
考虑分块做法,块长B
分析第一个操作
只需要维护数列的单调性,然后二分答案上二分就ok了
分析第二个操作
维护一个加法懒标记即可
口胡了一下感觉很简单
仔细分析一下第一个操作
二分找到一个“第k小值”,再进行check,check的过程中散块遍历一遍,整块二分找到最后一个小于等于x的(只有前面部分有贡献),分析一下时间复杂度,预处理 ,(分块完排序),二分答案
,二分
第二个操作
散块可以暴力然后重构,整块上懒标记,时间复杂度
总时间复杂度 maybe..
应该需要优化?
分析一下二分答案这块,我们不一定要把L定义无穷小,R定义无穷大,可以维护一下区间最大值区间最小值这样可以转化为差不多能卡过去了,我是这样干的,二分剪枝一下
分析一下散块区间加,不一定要的排序,我们可以把数列分成2块,没有加的和加的,两边其实都是有序的,因此可以用归并排序优化成
快长最优可能是..
小优化
1.不一定要把散块重构,如果没有询问到,可以不做,我们用线段树区间赋值的思想,修改后标记一下这个块需要重构,等询问的时候问到了再进行重构
void work(int l,int r){int p=pos[l];int q=pos[r];for(int i=p;i<=q;i++){if(re[i]){rebuild(i);re[i]=0;}}
}2.二分答案优化
if(k<1 || R-L+1<k){return -1;}3.块内二分优化
if(v[id].front()+add[id]>x){//没有比x小的return 0;}if(v[id].back()+add[id]<=x){//都是小于等于x的return r+1;//r-0+1;}4.维护区间最大值最小值优化
for(int i=p+1;i<=q-1;i++){//最后一个是最大res=max(res,v[i].back()+add[i]);}for(int i=p+1;i<=q-1;i++){//第一个是最小res=min(res,v[i].front()+add[i]);}完整代码
#include<iostream>
#include<cmath>
#include<algorithm>
#include<bitset>
#include<cstring>
#include<vector>
#define INF (1ll<<60)
using namespace std;
typedef long long ll;
const int N=1e5+9;
const int B=1e4+9;
namespace Lan {inline string sread() {string s=" ";char e=getchar();while(e==' '||e=='\n')e=getchar();while(e!=' '&&e!='\n')s+=e,e=getchar();return s;}inline void swrite(string s){for(char e:s)putchar(e);printf("\n");}inline ll read() {ll x=0,y=1;char c=getchar();while(!isdigit(c)){if(c=='-')y=-1;c=getchar();}while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=getchar();}return x*=y;}inline void write(ll x) {if(x<0){x=-x,putchar('-');}ll sta[35],top=0;do sta[top++]=x%10,x/=10;while(x);while(top)putchar(sta[--top]+'0');}
}using namespace Lan;
ll a[N];
int L[B],R[B],pos[N];
ll add[B];
int re[B];
vector<ll> v[B];
inline void rebuild(int id){v[id].clear();for(int i=L[id];i<=R[id];i++){v[id].push_back(a[i]);}sort(v[id].begin(),v[id].end());
}
inline int binary(int id,int x){int l=0,r=v[id].size()-1;if(v[id].front()+add[id]>x){//没有比x小的return 0;}if(v[id].back()+add[id]<=x){//都是小于等于x的return r+1;//r-0+1;}int res=0;while(l<=r){int mid=(l+r)>>1;if(v[id][mid]+add[id]<=x){//小于等于x,选大一点l=mid+1;res=mid+1;//小于等于x的有贡献}else{r=mid-1;}}return res;
}
inline ll getmax(int l,int r){ll res=-INF;int p=pos[l];int q=pos[r];if(p==q){for(int i=l;i<=r;i++){res=max(res,a[i]+add[pos[i]]);}}else{for(int i=l;i<=R[p];i++){res=max(res,a[i]+add[pos[i]]);}for(int i=L[q];i<=r;i++){res=max(res,a[i]+add[pos[i]]);}for(int i=p+1;i<=q-1;i++){//最后一个是最大res=max(res,v[i].back()+add[i]);}} return res;
}
inline ll getmin(int l,int r){ll res=INF;int p=pos[l];int q=pos[r];if(p==q){for(int i=l;i<=r;i++){res=min(res,a[i]+add[pos[i]]);}}else{for(int i=l;i<=R[p];i++){res=min(res,a[i]+add[pos[i]]);}for(int i=L[q];i<=r;i++){res=min(res,a[i]+add[pos[i]]);}for(int i=p+1;i<=q-1;i++){//第一个是最小res=min(res,v[i].front()+add[i]);}}return res;
}
inline int check(int l,int r,int x){int p=pos[l];int q=pos[r];int res=0;if(p==q){for(int i=l;i<=r;i++){if(a[i]+add[pos[i]]<=x){res++;}}}else{for(int i=l;i<=R[p];i++){if(a[i]+add[pos[i]]<=x){res++;}}for(int i=L[q];i<=r;i++){ if(a[i]+add[pos[i]]<=x){res++;}}for(int i=p+1;i<=q-1;i++){res+=binary(i,x);}}return res;
}
void work(int l,int r){int p=pos[l];int q=pos[r];for(int i=p;i<=q;i++){if(re[i]){rebuild(i);re[i]=0;}}
}
inline int kth(int k,int L,int R){if(k<1 || R-L+1<k){return -1;}work(L,R);int res=-1;ll l=getmin(L,R),r=getmax(L,R);while(l<=r){ll mid=(l+r)>>1;if(check(L,R,mid)<k){//选的值太小l=mid+1;}else{r=mid-1;res=mid;}}return res;
}
inline void modify(int l,int r,int k){int p=pos[l];int q=pos[r];if(p==q){for(int i=l;i<=r;i++){a[i]+=k;}re[p]=1;// rebuild(p);}else{for(int i=l;i<=R[p];i++){a[i]+=k;}re[p]=1;// rebuild(p);for(int i=p+1;i<=q-1;i++){add[i]+=k;}for(int i=L[q];i<=r;i++){a[i]+=k;}re[q]=1;// rebuild(q);}
}
int main(){// ios::sync_with_stdio(false);// cin.tie(0),cout.tie(0);int n,m;n=read();m=read();for(int i=1;i<=n;i++){a[i]=read();}int blo=sqrt(n);int t=ceil(1.0*n/blo);for(int i=1;i<=t;i++){L[i]=(i-1)*blo+1;R[i]=(i==t?n:i*blo);}for(int i=1;i<=t;i++){for(int j=L[i];j<=R[i];j++){pos[j]=i;}}for(int i=1;i<=n;i++){v[pos[i]].push_back(a[i]);}for(int i=1;i<=t;i++){sort(v[i].begin(),v[i].end());}for(int i=1;i<=m;i++){int op,l,r,k;op=read();l=read();r=read();k=read();if(op==1){write(kth(k,l,r));putchar('\n');}else{modify(l,r,k);}}return 0;
}相关文章:
P5356 [Ynoi2017] 由乃打扑克
我手把手教她打扑克 qwq 综合分析一下2个操作,查找区间第k小的值,感觉可以用主席树,区间修改那没事了 考虑分块做法,块长B 分析第一个操作 只需要维护数列的单调性,然后二分答案上二分就ok了 分析第二个操作 维护一个加法懒…...
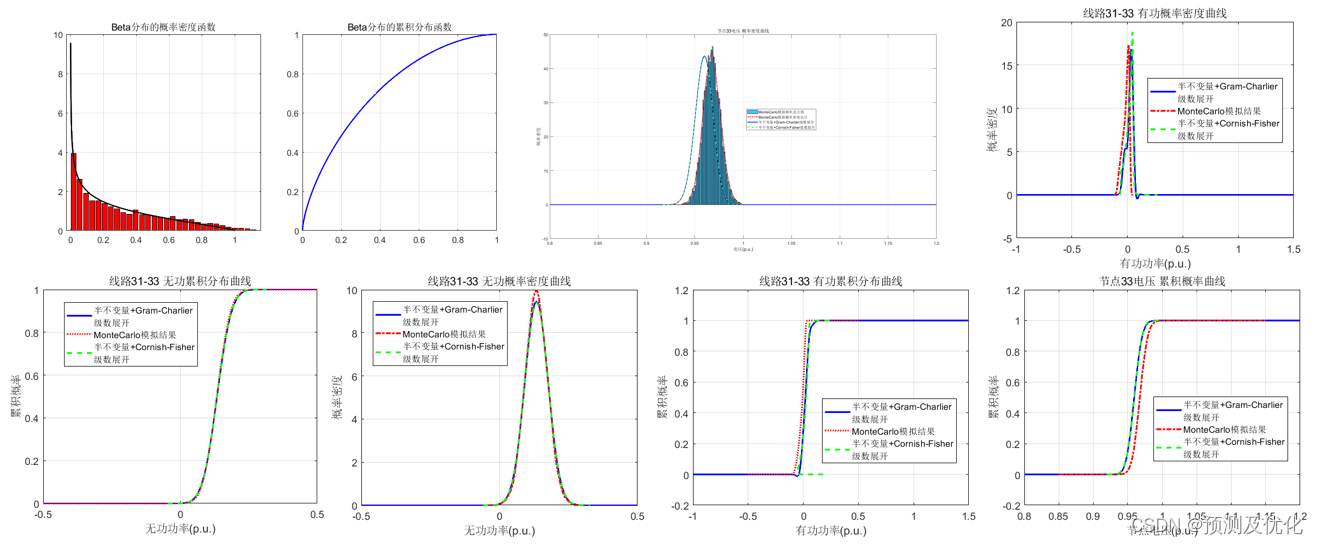
随机潮流应对不确定性?计及分布式发电的配电系统随机潮流计算程序代码!
前言 随着分布式电源在电力系统中所占比例的不断扩大,研究分布式发电对系统稳态运行的影响势在必行。带分布式发电的潮流计算常常用来评估其并网后对系统的影响,同时它也是分析分布式发电对电网稳定性的影响等其他理论研究工作的基础。然而,许多分布式发…...

Oracle表空间满清理方案汇总分享
目录 前言思考 一、第一种增加表空间的数据文件数量达到总容量的提升 二、第二种解决方案针对system和sysaux的操作 2.1SYSTEM表空间优化 2.2sysaux表空间回收 2.2.1针对sysaux的表空间爆满还有第二套方案维护 三、第三种解决方案使用alter tablespace resize更改表空间的…...

基于单片机数码管20V电压表仿真设计
**单片机设计介绍,基于单片机数码管20V电压表仿真设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机数码管20V电压表仿真设计的主要目的是通过单片机和数码管显示电路实现一个能够测量0到20V直流电压的电…...

SCI一区 | Matlab实现NGO-TCN-BiGRU-Attention北方苍鹰算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测
SCI一区 | Matlab实现NGO-TCN-BiGRU-Attention北方苍鹰算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测 目录 SCI一区 | Matlab实现NGO-TCN-BiGRU-Attention北方苍鹰算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测预测效果基本介绍模型…...
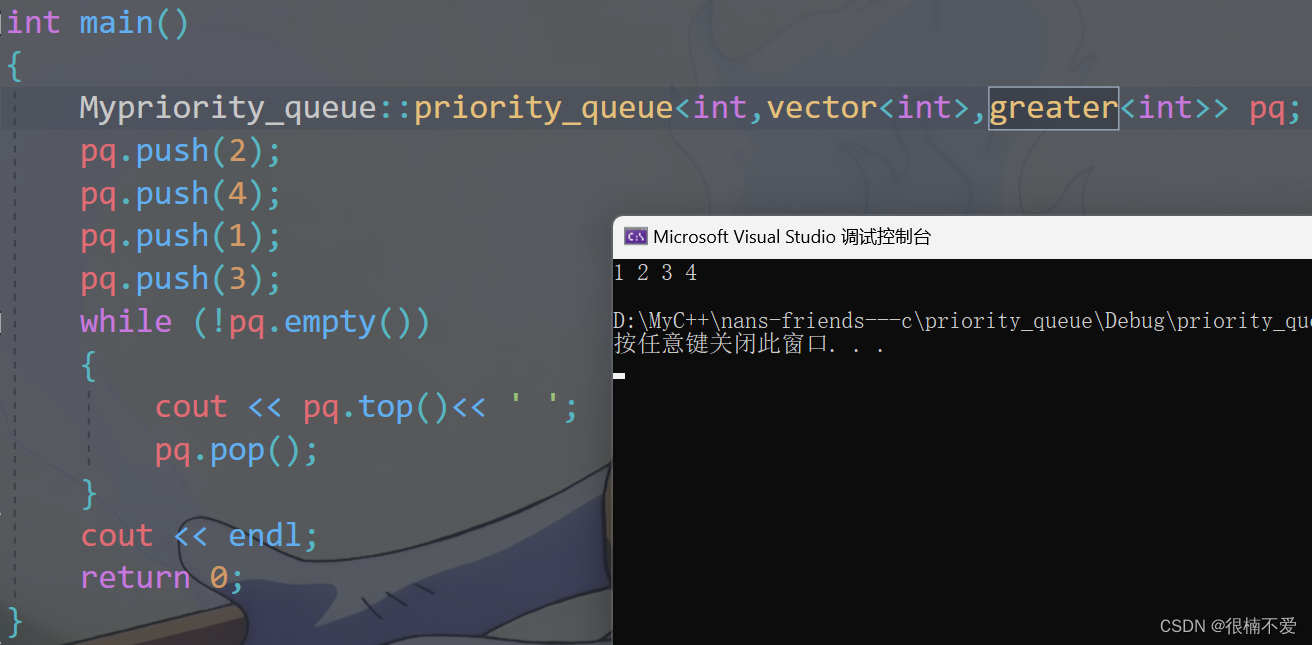
C++——优先级队列
前言:这篇文章我们继续来分享一个c的容器——优先级队列。 一.理解优先级 何为优先级一说?实际上就是有顺序的意思。 优先级队列,即有顺序的队列,是一个无需我们自己进行排序操作,在数据传入时就会由容器自己排好序的…...

docker部署jumpserver
1、安装Docker以及相关依赖 配置yum源 sudo yum install -y yum-utils sudo yum-config-manager \ --add-repo \ http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo sudo yum install docker-ce docker-ce-cli containerd.io docker-compose-plugin2、添加国…...
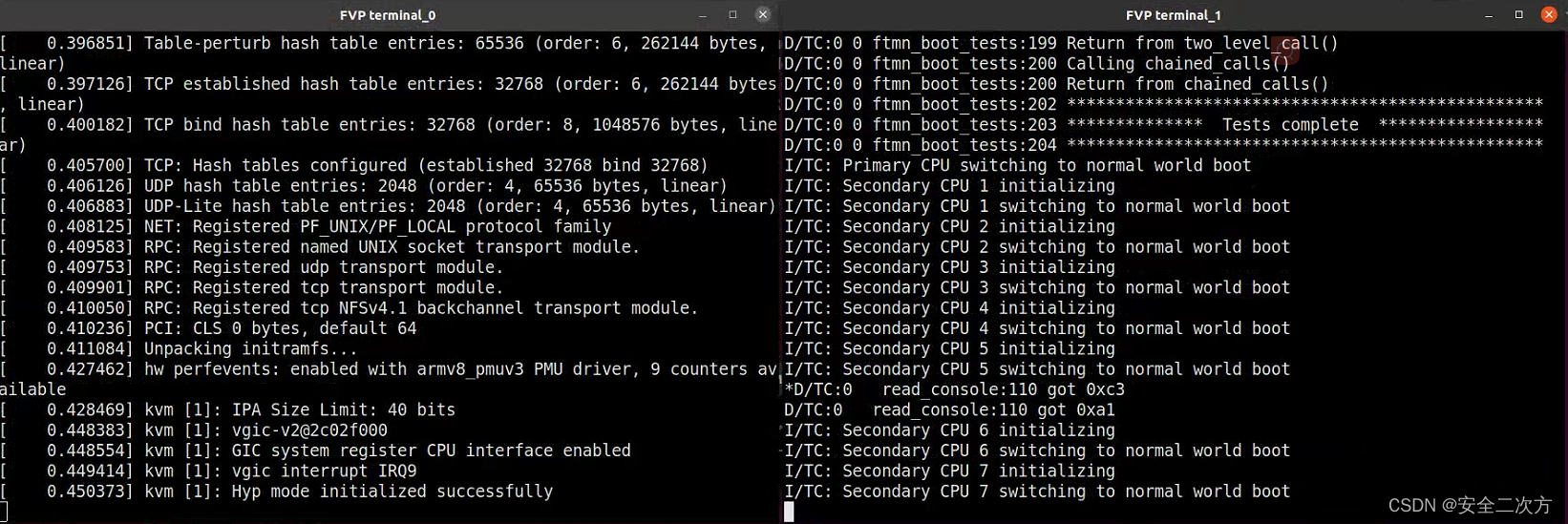
ARM FVP平台的terminal窗口大小如何设置
当启动ARM FVP平台时,terminal窗口太小怎么办?看起来非常累眼睛,本博客来解决这个问题。 首先看下ARM FVP平台对Host主机的需求: 通过上图可知,UART默认使用的是xterm。因此,我们需要修改xterm的默认字体设…...

003 静态代理
文章目录 StudentServiceImplStudentService.javaStudentServiceProxy.javaStudentServiceProxy1.javaStudentServiceProxyTest.java StudentServiceImpl package com.aistart.service.impl;import com.aistart.mapper.StudentMapper; import com.aistart.pojo.Student; import…...

基于JAX的二阶优化方法的实践
使用协作分支上的算法 git clone https://github.com/linjing-lab/jax.git cd jax git checkout linjing-lab cd examples在命令行预览方法 牛顿方法: cat newton_method.py拟牛顿法: cat bfgs_method.py在命令行运行程序 python newton_method.pyp…...

【计算机考研】408算法大题怎么练?
先说结论:基础阶段学好各个数据结构与,重点是数组、链表、树、图。然后强化阶段突破算法提 在基础阶段,并不需要过于专门地练习算法。相反,基础阶段的重点应该放在对各种数据结构原理的深入理解上。在我个人的经验中,…...

输入框验证数字类型
校验大于0的数,且小数点后最多为八位小数 let k /^(?!0(\.0)?$)\d(\.\d{1,8})?$/; console.log(k.test(0.00000001)); // true console.log(k.test(0.00000000)); // false console.log(k.test(0.12)); // true console.log(k.test(12.12)); // true输入0-1的数字…...

LeetCode 377——组合总和 Ⅳ
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 此题一看应该就是需要用到动态规划算法,假设我们以 f[d]表示总和为 d 的元素组合的个数,首先,我们遍历 nums 数组, 如果有 nums[i] < target,那么组…...

ubuntu同步网络时间
安装ntpdate sudo apt-get update sudo apt-get install ntpdate设置系统时间与网络时间同步 sudo ntpdate cn.pool.ntp.org设置时区亚洲上海 sudo cp /usr/share/zoneinfo/Asia/Shanghai /etc/localtime设置时间为24小时制 echo "LC_TIMEen_DK.UTF-8" >>/…...
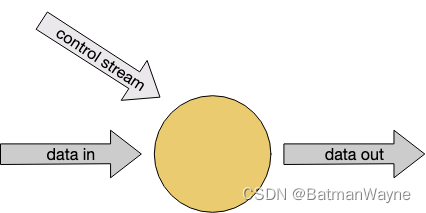
Flink学习(四)-数据管道 ETL
一、状态转换 map() 只适用于一对一的转换,即对每个进入算子的流元素,map() 将仅输出一个转换后的元素。 flatmap() 可以输出任意数量的元素,也可以一个都不发。 二、Keyed Streams keyBy() 相当于 sql 中的 group by,通过…...
Python可视化之Matplotlib
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1、解决坐标轴刻度负号乱码2、解决中文乱码问题3、图形展现形式 一、图形绘制1.折线图plot2.散点图plot&scatter3.柱状图plt.bar&条形图plt.barh4.直方…...
ChatGPT全方位解析:如何培养 AI 智能对话技能?
简介 ChatGPT 的主要优点之一是它能够理解和响应自然语言输入。在日常生活中,沟通本来就是很重要的一门课程,沟通的过程中表达的越清晰,给到的信息越多,那么沟通就越顺畅。 和 ChatGPT 沟通也是同样的道理,如果想要C…...

[C++/Linux] UDP编程
一. UDP函数 UDP(用户数据报协议,User Datagram Protocol)是一种无连接的网络协议,用于在互联网上交换数据。它允许应用程序发送数据报给另一端的应用程序,但不保证数据报能成功到达,也就是说,它…...

深入探索Linux的lsof命令
在Linux系统中,了解哪些文件被哪些进程打开对于系统管理和问题诊断是极其重要的。这正是lsof命令,即List Open Files,发挥其强大功能的场景。本文旨在详细介绍lsof的起源、底层原理、参数意义,常见用法,并详解其返回结…...

flowable 想改变正在运行的任务,实例版本为最新,需要改哪些表
在Flowable中,要改变正在运行的任务,你需要更新相关的流程定义,具体来说,可能涉及到以下几张表: ACT_RU_TASK(运行时任务):这张表包含了当前正在运行的任务信息。你可能需要更新该表…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
