计算系数(acwing,数论)
题目描述:
给定一个多项式 (ax+by)^k,请求出多项式展开后 x^n*y^m 项的系数。
输入格式:
共一行,包含 5 个整数,分别为 a,b,k,n,m,每两个整数之间用一个空格隔开。
输出格式:
输出共 1 行,包含一个整数,表示所求的系数,这个系数可能很大,输出对 10007取模后的结果。
数据范围:
0≤n,m≤k≤1000,
n+m=k,
0≤a,b≤1e6;
输入样例:
1 1 3 1 2
输出样例:
3分析步骤:
第一:理清思路:
-
通过看题目,我们清楚是要我们求解组合数的系数。所以如果我们要求解x^n*y^m的系数,系数就应该是Ck^n * a^n * b^m。那么这个Ck^n应该怎么求呢?这么多数如果我们一个一个硬算的话我们一定很困难和很耗时间的。
-
但是我们学过组合数的递推公式就是Cp^j = Cp-1^j-1+Cp-1^j。怎么理解这个公式呢?我们可以想:现在我从一堆苹果里面随便挑出了一个苹果,题目要求我们选择j个苹果,那么现在就分为两种情况一种是包含这个我们挑中的苹果,那么我们现在只要从p-1个总数中挑出j-1个苹果就可以了所以就是Cp-1^j-1;一种是不包含这个苹果,那么我们要从p-1个苹果中挑出j个苹果。只有这两种情况那么这两种情况加到一起就可以包括了所有的可能。那么只要递推过来就可以知道后面的情况了。
第二:书写主函数,构建整体框架:
-
我们把值全部都输入进去,这里有一个值得注意的地方这个点很细小,就是我们的a,b必须要先求一次模,为什么呢?因为我们的a和b最大都是1e6,如果最后和模相乘一下的话就会是1e10级别的数,那么一定会溢出。所以这里一定要模一下,不然过不去!
-
这里进入两层for循环利用好我们的递推公式,我们判断一下如果j是0的情况,就相当于从i个苹果里面选择0个的方案数,很明显一个都不选就是一种方案所以方案数就是1。
-
最终我们得出来的答案就是res[k][n](Ck^n)个方案。
-
我们已经把组合数的系数值算出来了,接下来就以要计算a和b的次方就行了
int main()
{cin>>a>>b>>k>>n>>m;a %= MOD , b %= MOD;for(int i = 0 ; i <= k ; i ++){for(int j = 0 ; j <= i ; j ++){if(!j) res[i][j] = 1;else res[i][j] = (res[i-1][j-1]+res[i-1][j])%MOD;}}int ans = res[k][n];for(int i = 0 ; i < n ; i ++) ans = ans * a % MOD;for(int i = 0 ; i < m ; i ++) ans = ans *b % MOD;cout<<ans;return 0;
}代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1100 , MOD = 10007;int a,b,k,n,m;
int res[N][N] ;int main()
{cin>>a>>b>>k>>n>>m;a %= MOD , b %= MOD;for(int i = 0 ; i <= k ; i ++){for(int j = 0 ; j <= i ; j ++){if(!j) res[i][j] = 1;else res[i][j] = (res[i-1][j-1]+res[i-1][j])%MOD;}}int ans = res[k][n];for(int i = 0 ; i < n ; i ++) ans = ans * a % MOD;for(int i = 0 ; i < m ; i ++) ans = ans *b % MOD;cout<<ans;return 0;
}
相关文章:

计算系数(acwing,数论)
题目描述: 给定一个多项式 (axby)^k,请求出多项式展开后 x^n*y^m 项的系数。 输入格式: 共一行,包含 5 个整数,分别为 a,b,k,n,m,每两个整数之间用一个空格…...
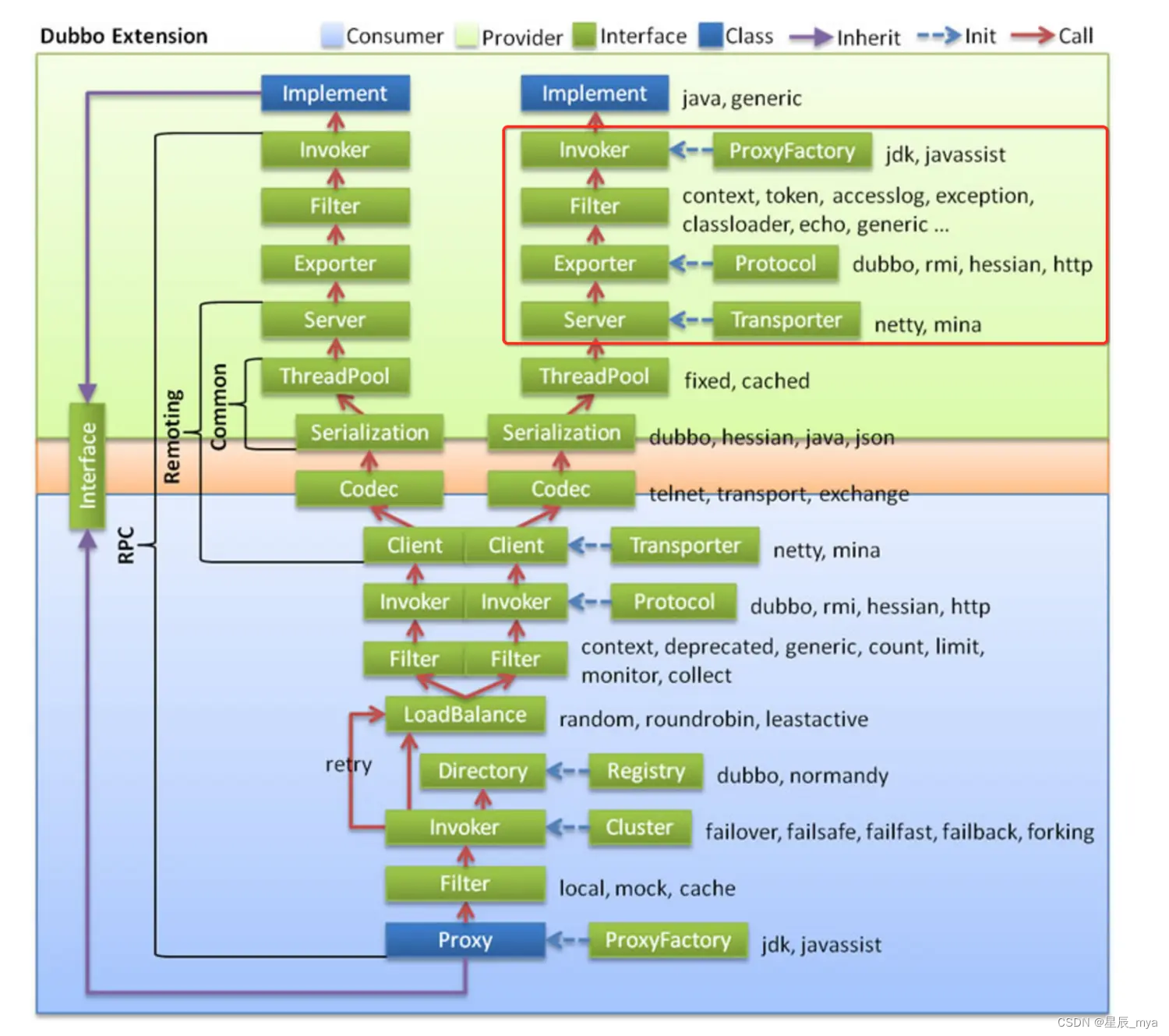
阿里面试题二
实在是太长了 重新开一篇吧 dubbo 服务暴露 Dubbo——服务调用、服务暴露、服务引用过程 - 简书 这两篇文章写的是极好 我现在查得资源强的可怕朋友们 服务降级 MockClusterInvoker 负载均衡策略 容错机制在哪里实现的源码 通信 NIO、BIO区别,NIO解决了什么…...
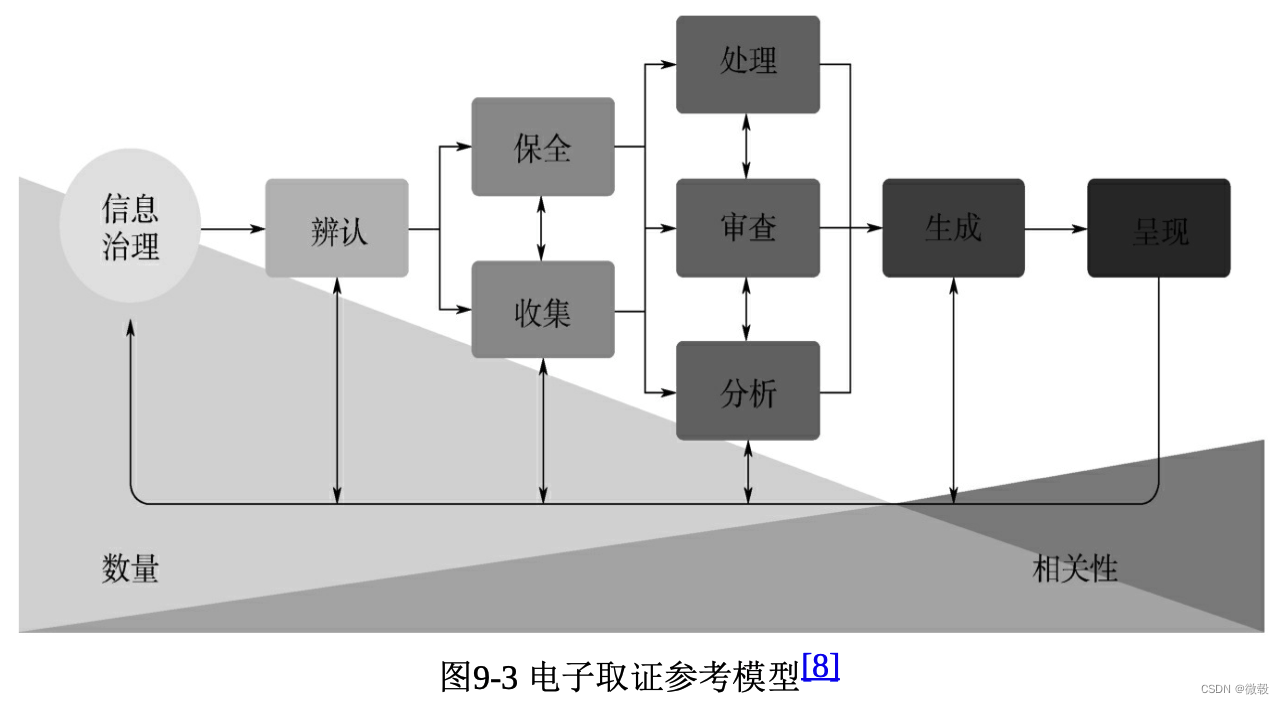
第9章 文件和内容管理
思维导图 9.1 引言 文件和内容管理是指针对存储在关系型数据库之外的数据和信息的采集、存储、访问和使用过程的管理。它的重点在于保持文件和其他非结构化或半结构化信息的完整性,并使这些信息能够被访问。文件和非结构化内容也应是安全且高质量的。 确保文件和内容…...
【Erlang】【RabbitMQ】Linux(CentOS7)安装Erlang和RabbitMQ
一、系统环境 查版本对应,CentOS-7,选择Erlang 23.3.4,RabbitMQ 3.9.16 二、操作步骤 安装 Erlang repository curl -s https://packagecloud.io/install/repositories/rabbitmq/erlang/script.rpm.sh | sudo bash安装 Erlang package s…...
-导出表)
pe格式从入门到图形化显示(七)-导出表
文章目录 前言一、什么是Windows PE格式中的导出表?二、解析导出表并显示1.导出表的结构2.解析导出表3.显示导出表 前言 通过分析和解析Windows PE格式,并使用qt进行图形化显示 一、什么是Windows PE格式中的导出表? PE文件格式的导出表是P…...
)
图片地址生成二维码(通过前端实现)
文章目录 概要安装插件代码实例 概要 要将图片地址生成二维码,你可以使用 QrCode 库(假设你已经在项目中引入了该库)。以下是一个简单的示例代码,演示了如何使用 QrCode 库将图片地址转换为二维码并显示在页面上 安装插件 先下载…...

window安装maven和hadoop3.1.4
前面的文章已讲解如何安装idea和进行基本设置,本文主要带着大家安装配置好maven和hadoop. 大家不用去官网下载,直接使用我发给大家的压缩文件,注意解压后的文件夹不要放在中文目录下,课堂上我们讲解过原因。 这是我电脑上的路径&a…...
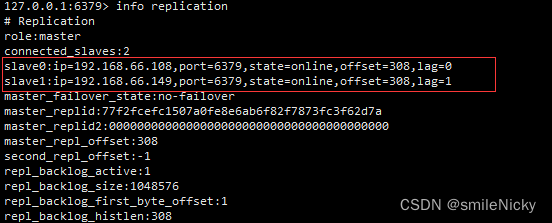
Redis系列之主从复制集群搭建
在上一篇博客,我们已经知道怎么搭建一个redis单机版,这篇博客基于之前的基础,来搭建一个redis主从同步,本博客框架是一主二从,一个主节点,其它两个从节点 实验环境 CentOS7Xshell6XFtp6Redis6.2.2 主从关…...

spring框架介绍
spring 1.优点 1)针对接口编程,解耦合 2)aop:变向切面编程,动态增加功能 3)方便集成框架,mybatis,hibernate,strust等 4)降低j2ee接口的使用难度 2.spring是干什么的 管理bean及bean…...

如果在 Ubuntu 系统中两个设备出现两个相同的端口号解决方案
问题描述: 自己的移动机器人在为激光雷达和IMU配置动态指定的端口时,发现激光雷达和深度相机配置的 idVendor 和 idProduct 相同,但是两个设备都具有不同的ttyUSB号,如下图所示 idVendor:代表着设备的生产商ID,由USB设…...

随手分享的APP链接,可能会让你“大型社死”
早晨上班路上,你在地铁百无聊赖地刷着短视频,看到一则好笑的,随手分享给了你的公司“饭搭子”,并配上了一串“哈哈哈哈哈哈”。 晚上下班路上你再次打开视频APP,发现首页弹窗给你推荐了一组“可能认识的人”ÿ…...

国内AI大模型已近80个,哪个最有前途?
根据中国新一代人工智能发展战略研究院发布的报告显示,目前全国已有3k+家人工智能企业,国内的AI大模型应该也近在200了!!! (原图图片过长了,这里就先放了20个) 面对如…...
美团一面:说说synchronized的实现原理?问麻了。。。。
引言 在现代软件开发领域,多线程并发编程已经成为提高系统性能、提升用户体验的重要手段。然而,多线程环境下的数据同步与资源共享问题也随之而来,处理不当可能导致数据不一致、死锁等各种并发问题。为此,Java语言提供了一种内置…...
P1123 取数游戏(dfs算法)
题目描述 一个 NM 的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻 8个格子中的一个即认为这两个数字相邻),求取出数字和最大是多少。 输入格式 第…...

交叉验证(Cross-Validation)
交叉验证的基本概念 交叉验证通常用于评估机器学习模型在未知数据上的性能。它将数据集分成k个不同的子集,然后进行k次训练和验证。在每次迭代中,选择一个子集作为测试集,其余的子集作为训练集。这样,每个子集都用作过测试集&…...
keras使用介绍)
【kears】(01)keras使用介绍
文章目录 一.特点二.keras如何支持TensorFlow、CNTK 和 Theano2.1 使用 TensorFlow 后端引擎训练和评估模型2.2 使用 TensorFlow 后端引擎训练和评估模型2.3 使用 Theano后端引擎训练和评估模型2.4 不同深度学习框架如何选择1.1 keras.datasets:包含多种常用数据集1…...

2. TypeScript 安装与环境配置指南
TypeScript 是 JavaScript 的一个超集,它为 JavaScript 增加了类型系统和对 ES6 的支持。TypeScript 不仅能够帮助开发者捕获代码中的错误,还能提供更好的编辑器支持,包括代码补全、接口提示等。本文将详细介绍如何在您的开发环境中安装和配置…...

python pygame库的略学
文章目录 概述1. pygame的初始化和退出2. 创建游戏窗口(1)set_mode()(2)set_capyion()(3)update() 3. 游戏循坏与游戏时钟4. 图形和文本绘制(1)图形绘制(2)文…...

大模型日报2024-04-09
大模型日报 2024-04-09 大模型资讯 苹果预告超越ChatGPT的新AI模型ReaLM 摘要: 苹果公司最新宣布,即将推出一款名为ReaLM的人工智能模型。这款AI技术在理解复杂屏幕用户指令方面表现出高超的能力,并能与用户进行自然流畅的对话。ReaLM的推出预示着苹果在…...
)
抖音视频如何下载保存(方法分享)
有时刷抖音视频,看的喜欢的视频想要下载到本地,但是有很多视频无法下载或者下载下来是有水印的,那怎么办呢? 抖音视频下载有两种情况: 一种是可以直接点击分享下载,然后可以直接点击保存到相册。 视频就自动下载…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
