当前位置： 首页 > news >正文

Windows系统上运行appium连接iOS真机自动化测试

news 2026/2/9 3:00:02

步骤：

1、windows安装tidevice工具

2、Mac系统打包安装WebDriverAgent（WDA）工具

3、安装Appium

4、连接iOS手机

iOS自动化的实现和执行都依赖Mac系统，因为需要通过Xcodebuild编译安装WDA (WebDriverAgent)到iOS设备中，通过WDA实现对被测应用进行操作。而Windows系统无法运行Xcode工具，所以无法运行iOS自动化测试

安装tidevice工具就可以做到在Windows上运行 iOS自动化测试

阿里团队开源了一个内部使用的 iOS自动化工具 ： tidevice ，更方便、简单的脱离Mac的限制。

在Windows上配置安装tidevice：

一、依赖环境

1、安装python3.6及以上版本

2、配置python系统环境变量

3、安装pip（pip install XXX）

二、安装tidevice

1、打开cmd，输入命令:

pip3 install -U "tidevice[openssl]"

如图：

           

2、查看是否安装成功：

tidevice version
#或
tidevice -v

如图：

                   

3、列出连接的设备，输入命令

tidevice list
#或
tidevice list --json

如图：

相关文章：

Windows系统上运行appium连接iOS真机自动化测试

步骤： 1、windows安装tidevice工具 2、Mac系统打包安装WebDriverAgent（WDA）工具 3、安装Appium 4、连接iOS手机 iOS自动化的实现和执行都依赖Mac系统，因为需要通过Xcodebuild编译安装WDA (WebDriverAgent)到iOS设备中，通过WDA实现对被测应用进行操作。而Windows系统无…...

编程日记 2024/4/10 9:29:36

vue3使用jsQR解析二维码

1.了解jsQR jsQR是一个纯javascript脚本实现的二维码识别库&#xff0c;不仅可以在浏览器端使用&#xff0c;而且支持后端node.js环境。jsQR使用较为简单&#xff0c;有着不错的识别率。 2.效果图 3.二维码 4.下载jsqr包 npm i -d jsqr5.代码 <script setup> import …...

编程日记 2024/4/10 9:28:35

李廉洋：4.10黄金原油早间走势最新分析及策略。

过去半小时&#xff08;美国&#xff09;股市的下跌是由动量股推动的。这巧妙地凸显了由于动量因素的极度拥挤而导致的高风险。通常情况下&#xff0c;这将预示着低于平均水平的市场回报&#xff0c;但由于今年势头股的表现异常出色&#xff0c;以及对冲基金对这一因素的创纪录…...

编程日记 2024/4/10 9:25:32

Kotlin作用域函数:let、also、run、apply、with

​​​​​​​ let函数 使用场景&#xff1a;可空变量的操作&#xff0c;无需判空 p?.let {it.name "lily"it.age "21"} also函数 使用场景&#xff1a;多个扩展函数链式调用&#xff08;返回值是本身&#xff09; p?.also {it.name "den…...

编程日记 2024/4/10 9:24:31

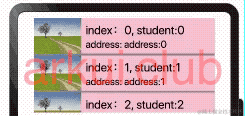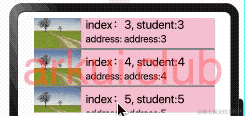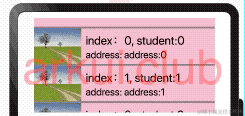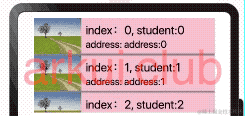
鸿蒙ArkUI开发学习：【渲染控制语法】

ArkUI开发框架是一套构建 HarmonyOS / OpenHarmony 应用界面的声明式UI开发框架&#xff0c;它支持程序使用 if/else 条件渲染&#xff0c; ForEach 循环渲染以及 LazyForEach 懒加载渲染。本节笔者介绍一下这三种渲染方式的使用。 if/else条件渲染 使用 if/else 进行条件渲染…...

编程日记 2024/4/10 9:23:29

https的配置和使用（以腾讯云为例）

1、注册域名 2、获取证书 3、下载证书 下载下来的证书所有格式 4、在服务器上下载nginx并配置 nginx的配置文件 如下 server {listen 80;listen 443 ssl;server_name delegate.letspiu.net.cn;ssl on; #开启ssl#指定证书位置ssl_certificate /etc/ss…...

编程日记 2024/4/10 9:19:25

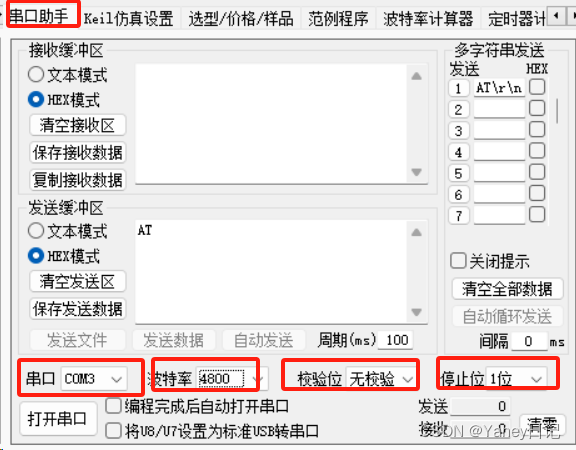
STC89C52学习笔记（七）

STC89C52学习笔记&#xff08;七&#xff09; 综述&#xff1a;本文介绍了串口以及讲述了串口相关寄存器如何配置并给予相关代码。 一、修改代码注意事项 在修改代码时不要一次性加入一堆代码&#xff0c;不利于定位错误。可以先注释一些代码&#xff0c;待解决完毕问题后再…...

编程日记 2024/4/10 9:17:23

嵌入式|蓝桥杯STM32G431（HAL库开发）——CT117E学习笔记16：蓝桥杯编程手册

一、要背的函数汇总&#xff08;以例子形式&#xff09; 1.GPIO相关 输出&#xff1a;HAL_GPIO_WritePin(GPIOC,GPIO_PIN_8 | GPIO_PIN_9,GPIO_PIN_SET) 输入&#xff1a;HAL_GPIO_ReadPin(GPIOB, GPIO_PIN_0) 翻转&#xff1a;HAL_GPIO_TogglePin(GPIOC,0xFF) 2.LCD相关 …...

编程日记 2024/4/10 9:14:19

doris2.0.7 安装

1&#xff0c;查看操作系统 lsb_release -a #Distributor ID: Ubuntu #Description: Ubuntu 22.04.3 LTS #Release: 22.04 #Codename: jammy 2&#xff0c;安装zip&#xff0c;mysql-client apt install mysql-client apt install zip 3&#xff0c;安装jdk apt inst…...

编程日记 2024/4/10 9:10:14

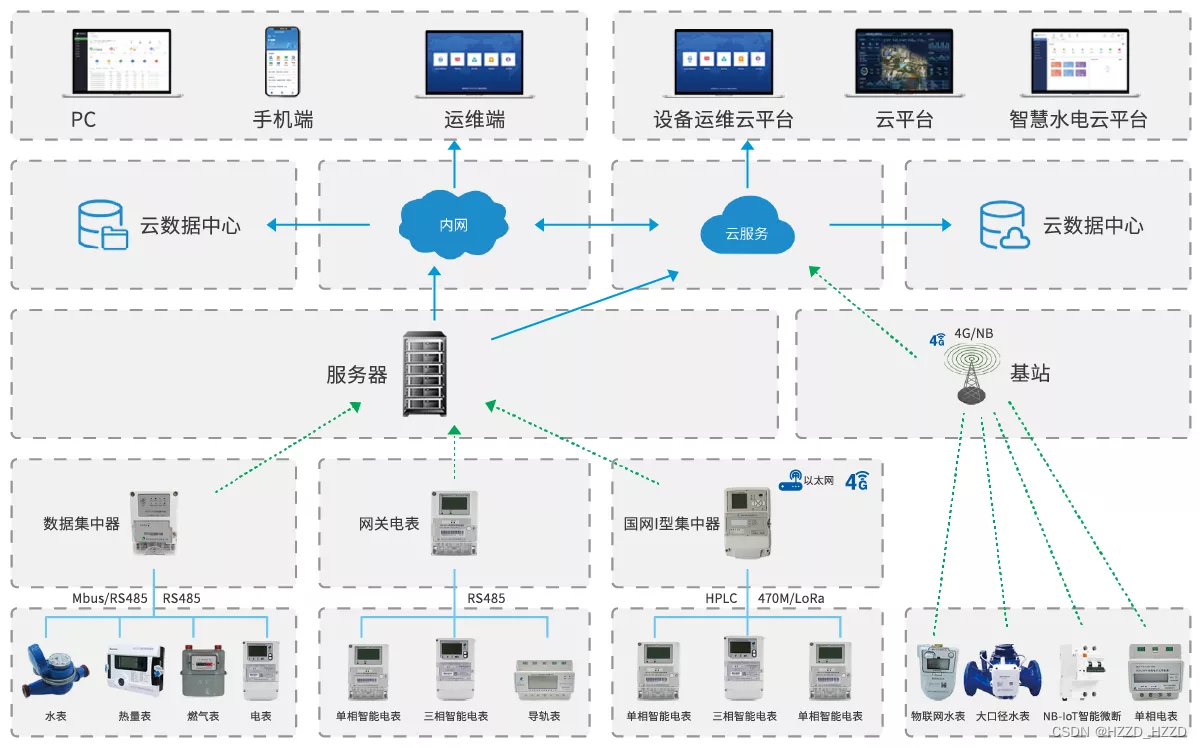
智慧园区水电能源监控管理系统

随着智慧城市的快速发展&#xff0c;智慧园区作为城市智能化的重要组成部分&#xff0c;其能源监控管理系统显得尤为关键。智慧园区水电能源监控管理系统&#xff0c;是利用先进的信息技术和自动控制技术&#xff0c;对园区内的水电能源使用进行实时监控、管理和优化的综合性智…...

编程日记 2024/4/10 9:09:13

Kafka基础/1

Kafka 概念 Kafka 是一个分布式的流媒体平台。 应用&#xff1a;消息系统、日志收集、用户行为追踪、流式处理 特点&#xff1a;高吞吐量、消息持久化、高可靠性、高扩展性 术语&#xff1a; broker&#xff1a;Kafka 的服务器&#xff0c;Kafka 当中每一台服务器&#xf…...

编程日记 2024/4/10 9:08:12

Jupyter Notebook中常见的快捷键

Jupyter Notebook的快捷键主要分为两种模式&#xff1a;命令模式和编辑模式。 在命令模式下&#xff0c;键盘输入用于运行程序命令&#xff0c;此时单元格框线是蓝色的&#xff1b; 在编辑模式下&#xff0c;可以往单元格中键入代码或文本&#xff0c;此时单元格框线是绿色的…...

编程日记 2024/4/10 9:07:11

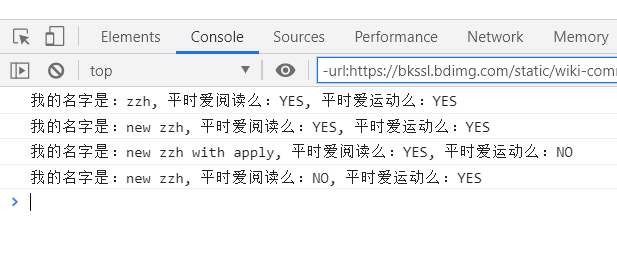
《前端面试题》- JS基础 - call()、apply()、bind() 的区别

call 、bind 、 apply 这三个函数的功能都是改变this的指向问题&#xff0c;但是也存在一定的区别。 call 的参数是直接放进去的&#xff0c;第二第三第 n 个参数全都用逗号分隔,apply 的所有参数都必须放在一个数组里面传进去bind 除了返回是函数以外&#xff0c;它 的参数和…...

编程日记 2024/4/10 9:06:09

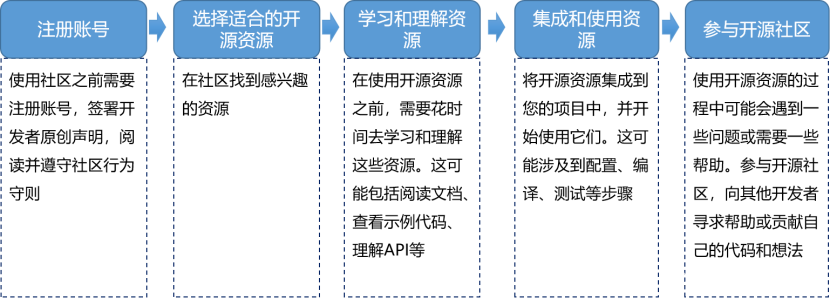
开源软件技术社区方案

开源软件技术社区是一个由开发者、贡献者、用户和维护者组成的共享平台&#xff0c;主要目的是打造技术、软件产品良性互动、开源技术安全可控的软件生态环境&#xff0c;实现可复用应用或服务的快速部署与使用、完成资源与能力的高度共享、促进社区成员的共建共赢&#xff0c;…...

编程日记 2024/4/10 9:05:08

【开源书籍】深入讲解内核网络、Kubernetes、ServiceMesh、容器等云原生相关技术。

项目地址&#xff1a;GitHub - isno/theByteBook: ⭐ 【开源书籍】深入讲解内核网络、Kubernetes、ServiceMesh、容器等云原生相关技术。经历实践检验的 DevOps、SRE指南。如发现错误&#xff0c;谢谢提issue 深入架构原理与实践 这是什么&#xff1f; 这是一本关于架构设计…...

编程日记 2024/4/10 9:04:07

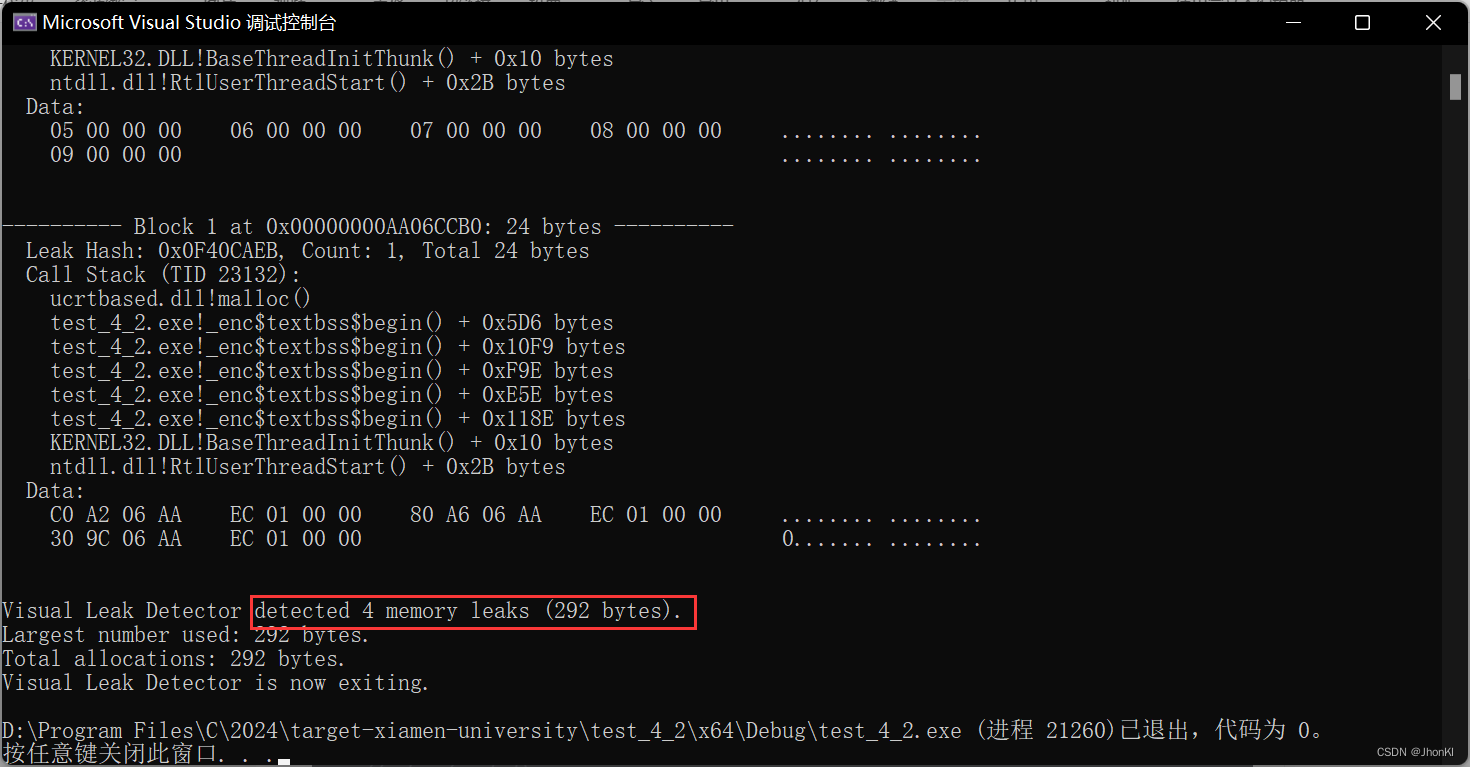
【C语言】“vid”Microsoft Visual Studio安装及应用（检验内存泄露）

文章目录 前言安装包获取配置VLD完成 前言 我们在写代码时往往容易存在内存泄漏的情况&#xff0c;所以存在这样一个名为VLD的工具用来检验内存泄漏&#xff0c;现在我来教大家安装一下 安装包获取 vld下载网址&#xff1a;https://github.com/KindDragon/vld/releases/tag/…...

编程日记 2024/4/10 9:03:05

Accuracy准确率,Precision精确率,Recall召回率,F1 score

真正例和真反例是被正确预测的数据&#xff0c;假正例和假反例是被错误预测的数据。然后我们需要理解这四个值的具体含义&#xff1a; TP&#xff08;True Positive&#xff09;&#xff1a;被正确预测的正例。即该数据的真实值为正例&#xff0c;预测值也为正例的情况&#xf…...

编程日记 2024/4/10 9:01:03

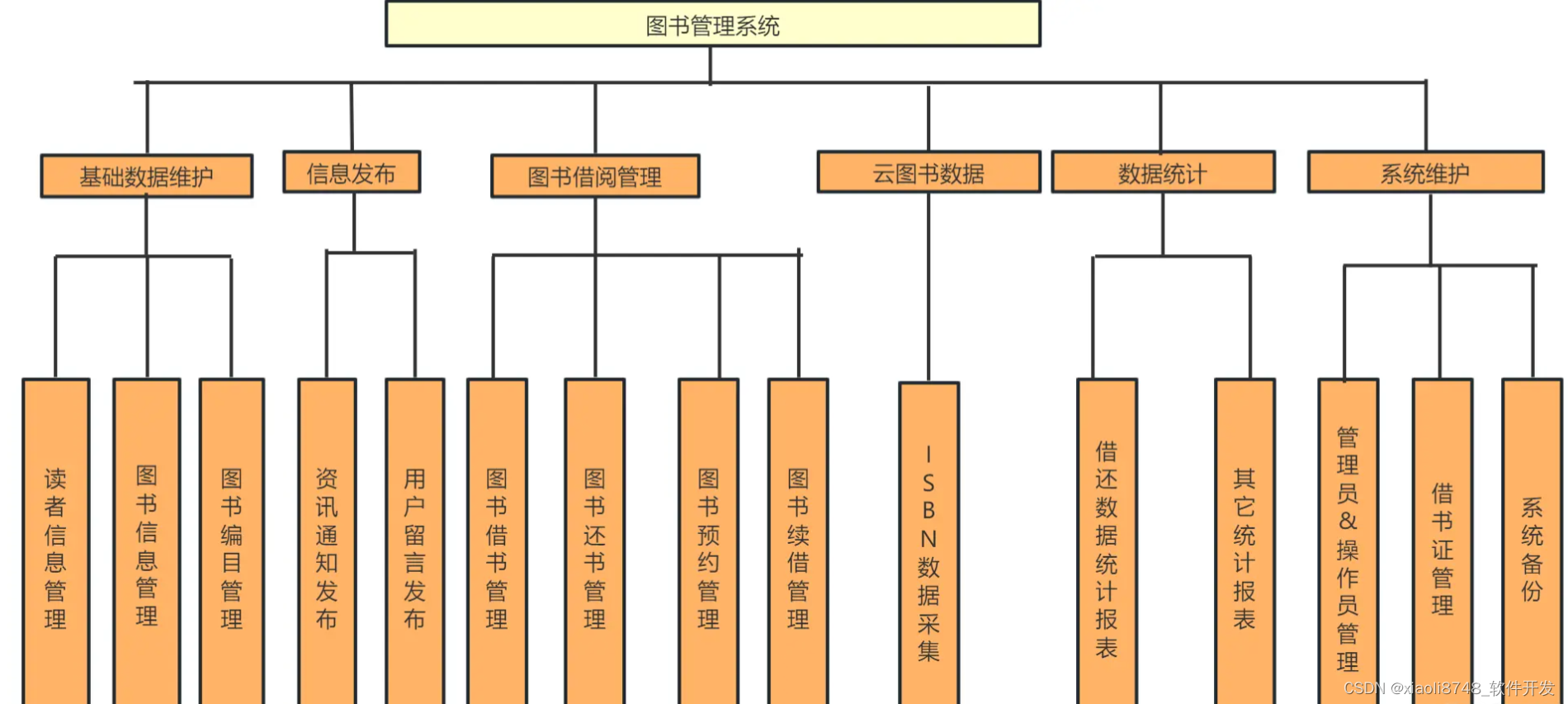
系统架构最佳实践 -- 智慧图书管理系统架构设计

随着数字化时代的到来&#xff0c;智慧图书管理系统在图书馆和机构中扮演着重要的角色。一个优秀的图书管理系统不仅需要满足基本的借阅管理需求&#xff0c;还需要具备高效的性能、良好的扩展性和稳定的安全性。本文将讨论智慧图书管理系统的架构设计与实现&#xff0c;以满足…...

编程日记 2024/4/10 8:53:55

网络基础三——IP协议补充和Mac帧协议

全球网络及网段划分的理解 ​ 根据国家组织地区人口综合评估进行IP地址范围的划分&#xff1b; ​ 假设前8位用来区分不同的国家&#xff0c;国际路由器负责全球数据传输&#xff0c;子网掩码为IP/8&#xff1b;次6位区分不同的省份&#xff0c;国内路由器负责全国数据的传输…...

编程日记 2024/4/10 8:50:52

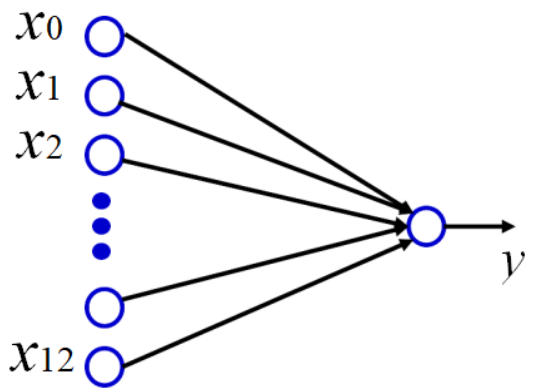
人工智能——深度学习

4. 深度学习 4.1. 概念 深度学习是一种机器学习的分支&#xff0c;旨在通过构建和训练多层神经网络模型来实现数据的高级特征表达和复杂模式识别。与传统机器学习算法相比&#xff0c;深度学习具有以下特点&#xff1a; 多层表示学习&#xff1a;深度学习使用深层神经网络&a…...

编程日记 2024/4/10 8:48:50

【Linux】shell脚本忽略错误继续执行

在 shell 脚本中&#xff0c;可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行&#xff0c;可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令&#xff0c;并忽略错误 rm somefile…...

编程新知 2025/9/11 15:27:32

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具&#xff0c;该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具&#xff0c;其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利&#xff0c;如安装和调试…...

编程新知 2026/1/21 18:20:51

sqlserver 根据指定字符 解析拼接字符串

DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

编程新知 2025/10/29 4:33:03

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2026/1/29 14:27:00

推荐 github 项目:GeminiImageApp(图片生成方向，可以做一定的素材)

推荐 github 项目:GeminiImageApp(图片生成方向&#xff0c;可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

编程新知 2026/1/25 10:41:07

【LeetCode】算法详解#6 ---除自身以外数组的乘积

1.题目介绍 给定一个整数数组 nums&#xff0c;返回 数组 answer &#xff0c;其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&#xff0c;且在 O…...

编程新知 2026/2/1 20:47:10

es6+和css3新增的特性有哪些

一&#xff1a;ECMAScript 新特性&#xff08;ES6&#xff09; ES6 (2015) - 革命性更新 1&#xff0c;记住的方法&#xff0c;从一个方法里面用到了哪些技术 1&#xff0c;let /const块级作用域声明2&#xff0c;**默认参数**&#xff1a;函数参数可以设置默认值。3&#x…...

编程新知 2025/11/26 7:13:37

【WebSocket】SpringBoot项目中使用WebSocket

1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖&#xff0c;添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

编程新知 2025/9/20 3:28:39

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.

这个警告表明您在使用Vue的esm-bundler构建版本时&#xff0c;未明确定义编译时特性标志。以下是详细解释和解决方案&#xff1a; ‌问题原因‌&#xff1a; 该标志是Vue 3.4引入的编译时特性标志&#xff0c;用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...

编程新知 2025/11/2 19:29:07