详解init 容器
什么是init容器
init 容器是一种特殊容器,在 Pod 内的应用容器启动之前运行。Init 容器可以包括一些应用镜像中不存在的实用工具和安装脚本。
你可以在 Pod 的规约中与用来描述应用容器的 containers 数组平行的位置指定 Init 容器
每个 Pod 中可以包含多个容器, 应用运行在这些容器里面,同时 Pod 也可以有一个或多个先于应用容器启动的 Init 容器。
Init 容器与普通的容器非常像,除了如下两点:
- 它们总是运行到完成。
- 每个都必须在下一个启动之前成功完成。
如果 Pod 的 Init 容器失败,kubelet 会不断地重启该 Init 容器直到该容器成功为止。 然而,如果 Pod 对应的 restartPolicy 值为 “Never”,并且 Pod 的 Init 容器失败, 则 Kubernetes 会将整个 Pod 状态设置为失败。
为 Pod 设置 Init 容器需要在 Pod 规约中添加 initContainers 字段, 该字段以 Container 类型对象数组的形式组织,和应用的 containers 数组同级相邻。 参阅 API 参考的容器章节了解详情。
Init 容器的状态在 status.initContainerStatuses 字段中以容器状态数组的格式返回 (类似 status.containerStatuses 字段)。
和普通容器的不同之处
Init 容器支持应用容器的全部字段和特性,包括资源限制、数据卷和安全设置。
同时 Init 容器不支持 lifecycle、livenessProbe、readinessProbe 和 startupProbe, 因为它们必须在 Pod 就绪之前运行完成。
如果为一个 Pod 指定了多个 Init 容器,这些容器会按顺序逐个运行。 每个 Init 容器必须运行成功,下一个才能够运行。当所有的 Init 容器运行完成时, Kubernetes 才会为 Pod 初始化应用容器并像平常一样运行。
如何使用 Init 容器
因为 Init 容器具有与应用容器分离的单独镜像,其启动相关代码具有如下优势:
-
Init 容器可以包含一些安装过程中应用容器中不存在的实用工具或个性化代码。 例如,没有必要仅为了在安装过程中使用类似
sed、awk、python或dig这样的工具而去FROM一个镜像来生成一个新的镜像。 -
应用镜像的创建者和部署者可以各自独立工作,而没有必要联合构建一个单独的应用镜像。
-
与同一 Pod 中的多个应用容器相比,Init 容器能以不同的文件系统视图运行。因此,Init 容器可以被赋予访问应用容器不能访问的 Secret 的权限。
-
由于 Init 容器必须在应用容器启动之前运行完成,因此 Init 容器提供了一种机制来阻塞或延迟应用容器的启动,直到满足了一组先决条件。 一旦前置条件满足,Pod 内的所有的应用容器会并行启动。
-
Init 容器可以安全地运行实用程序或自定义代码,而在其他方式下运行这些实用程序或自定义代码可能会降低应用容器镜像的安全性。 通过将不必要的工具分开,你可以限制应用容器镜像的被攻击范围
相关文章:

详解init 容器
什么是init容器 init 容器是一种特殊容器,在 Pod 内的应用容器启动之前运行。Init 容器可以包括一些应用镜像中不存在的实用工具和安装脚本。 你可以在 Pod 的规约中与用来描述应用容器的 containers 数组平行的位置指定 Init 容器 每个 Pod 中可以包含多个容器&…...

RequestResponseBodyMethodProcessor
既是一个参数解析器,也是一个返回结果处理器。 1.持有消息转换器的集合 protected final List<HttpMessageConverter<?>> messageConverters;2.作为参数解析器,例如对RequestBody标识的参数进行解析 判断是否支持当前类型的参数 Overrid…...
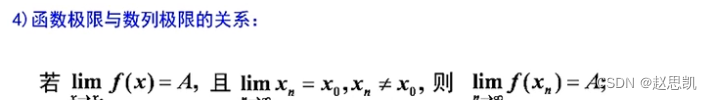
函数的极限
目录 函数的极限 函数极限的定义: 例题: 左右极限: 自变量趋于无穷大时函数的极限: 例题: 函数极限的性质: 函数极限与数列极限之间的关系: 函数的极限 函数极限的定义: 一句…...

dnf命令使用
1. 简介 DNF是新一代的rpm软件包管理器。他首先出现在 Fedora 18 这个发行版中。而最近,它取代了yum,正式成为 Fedora 22 的包管理器 DNF包管理器克服了YUM包管理器的一些瓶颈,提升了包括用户体验,内存占用,依赖分析…...
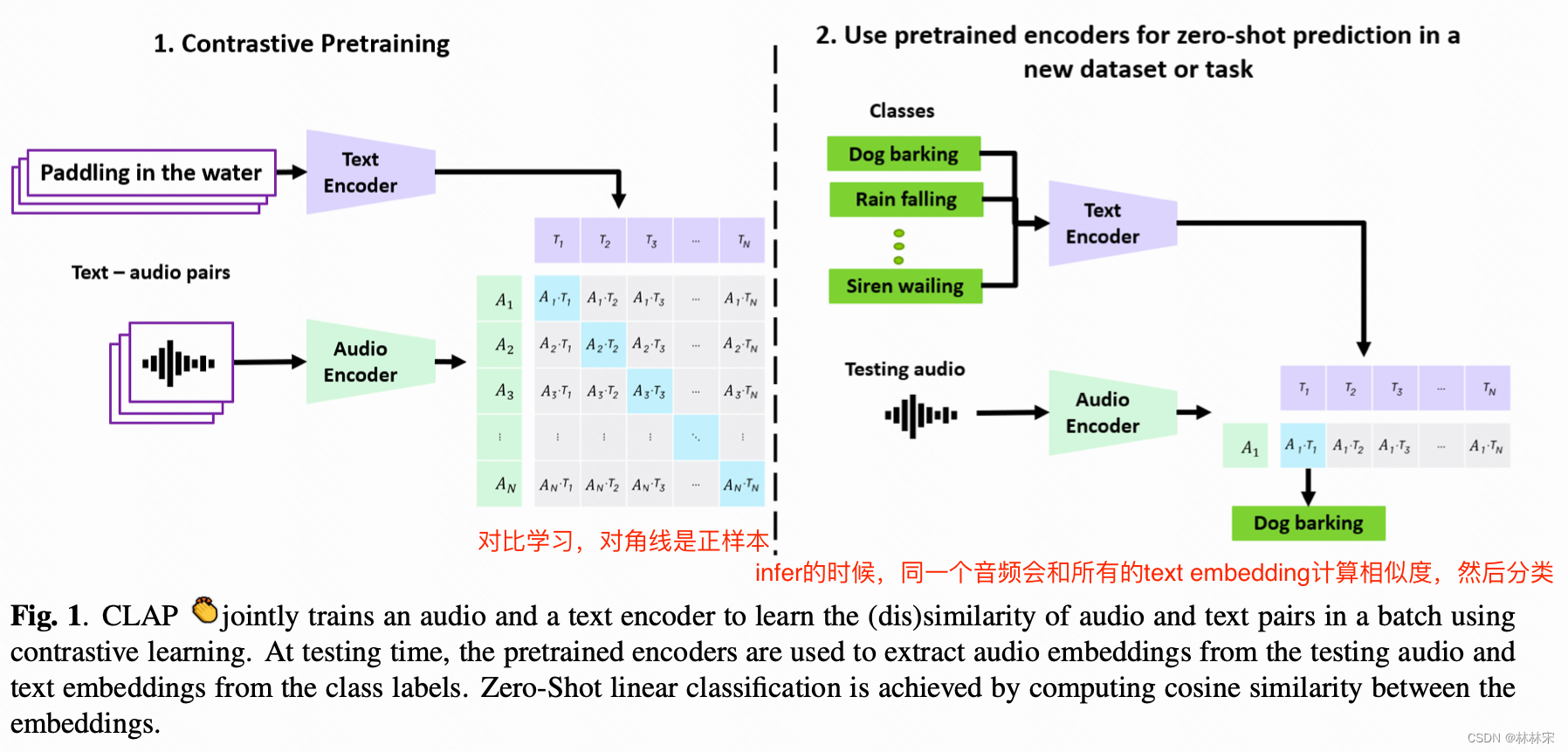
CLIP CLAP
文章目录CLIPabstractintroCLAP: LEARNING AUDIO CONCEPTS FROM NATURAL LANGUAGE SUPERVISIONabstractmethodCLIP open AI2021.2代码&预训练模型 abstract 原有的基于有监督数据训练的计算机分类任务,在面对新的分类目标时泛化性和可用性都会变差࿱…...

Debezium报错处理系列之五十二:解决Sql Server数据库安装后修改主机名导致sqlserver数据库实例名称没有修改从而无法设置CDC的问题
Debezium报错处理系列之五十二:解决Sql Server数据库安装后修改主机名导致sqlserver数据库实例名称没有修改从而无法设置CDC的问题 一、完整报错二、错误原因三、解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make sure that t…...

scratch老鹰捉小鸡 电子学会图形化编程scratch等级考试二级真题和答案解析2022年12月
目录 scratch老鹰捉小鸡 一、题目要求 1、准备工作 2、功能实现 二、案例分析 <...
)
概率论小课堂:公理化过程(大数据方法解决问题的理论基础)
文章目录 引言I 初等概率论1.1 19世纪概率论的最大难题1.2 伯努利版本的大数定理1.3 切比雪夫版本的大数定理II 现代概率论(用公理来描述概率论)2.1 柯尔莫哥洛夫2.1 用公理来描述概率论III 最基本的概率论定理3.1 互补事件的概率之和等于13.2 不可能事件的概率为零引言 前苏…...

WOW64 IsWow64Process GetNativeSystemInfoWindows System32 SysWOW64
最近开发有遇到这方面的一些知识点,在此记录下。首先,什么是WOW64?在知道这个之前我觉得需要了解一下,C:\\Windows\\System32和C:\\Winodws\\SysWOW64这两个文件夹的区别,Windows系统最开始的时候出的就是32bit的系统&…...

Spring Boot 3.0系列【10】核心特性篇之应用配置的高阶用法
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本3.0.3 源码地址:https://gitee.com/pearl-organization/study-spring-boot3 文章目录 前言1. 命令行2. JSON3. 外部化配置3.1 配置文件加载位置3.2 导入配置3.2 属性占位符4. 加密配置5. 加载YML配置文件6. 配…...

Java int类型数值比较总结
如果是int类型,判断相等的话直接使用 ""来判断,例如: int i 10; int j 10; System.out.print(i j); 如果是Integer类型,则可以使用equals方法进行相等比较。 int与Integer的基本使用对比 (…...
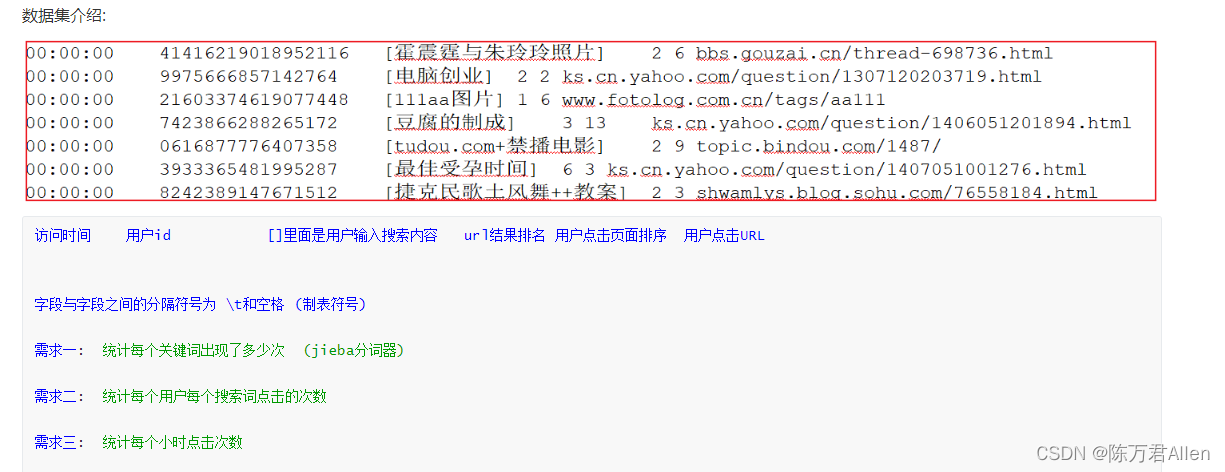
Pyspark基础入门5_RDD的持久化方法
Pyspark 注:大家觉得博客好的话,别忘了点赞收藏呀,本人每周都会更新关于人工智能和大数据相关的内容,内容多为原创,Python Java Scala SQL 代码,CV NLP 推荐系统等,Spark Flink Kafka Hbase Hi…...

汽车娱乐系统解决方案
Danlaw在汽车和航空航天行业里是全球知名的技术和服务供应商,致力于提供更加安全与智能的系统。Danlaw以突破性技术和高效开发、动态环境的自适应解决方案而闻名。Danlaw优秀的联网汽车解决方案使之成为全球大型互联设备供应商之一。 一 信息娱乐系统测试 | 风丘科…...

Go语言结构体,这一篇就够了
Go语言结构体,这一篇就够了1.结构体的概念2.结构体的定义3.结构体的实例化4.结构体初始化5.构造函数6.方法和接收者方法接收者7.嵌套结构体8.结构体的“继承”9.结构体与JSON序列化10.结构体标签(Tag)Go语言中没有“类”的概念,也…...

【python】各种排序算法代码大集合
超级好用的口诀: 时间复杂度:快些以nlogn的速度归队。 稳定性:心情不稳定,快些选一堆好友来聊天吧。 直接插容易插变O(N),起泡起得好变O(N).(初始序列已经有序) 插入排序法在近乎有序的情况下,效率特别高,通过插入排序,可以引申出希尔排序 归并排序:左半部分排好序…...
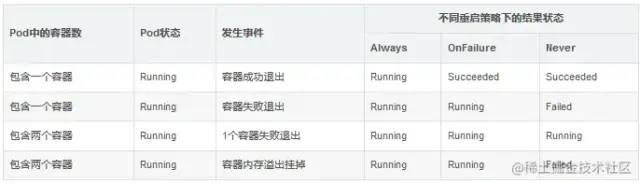
K8S Pod健康检查
因为 k8s 中采用大量的异步机制、以及多种对象关系设计上的解耦,当应用实例数 增加/删除、或者应用版本发生变化触发滚动升级时,系统并不能保证应用相关的 service、ingress 配置总是及时能完成刷新。在一些情况下,往往只是新的 Pod 完成自身…...
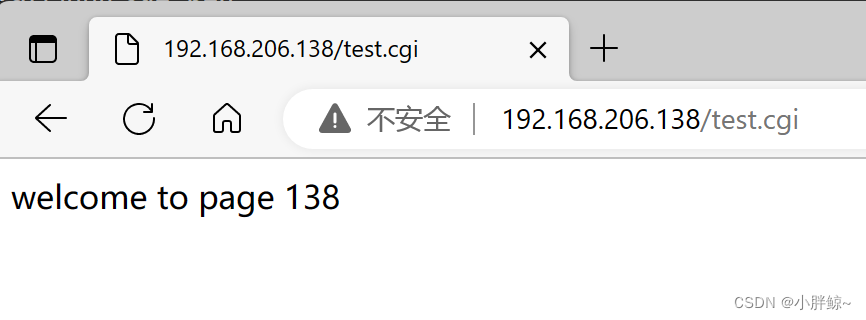
NFS服务器与CGI程序详解
目录 NFS 服务器 一,NFS 服务器简介 二,NFS的使用 三,客户端使用 autofs 自动挂载 1,autofs产生的原因 四,autofs的安装与配置文件 五,autofs的使用 www服务器---cgi程序 CGI程序的应用 NFS 服务器 一&a…...

可视化项目管理,控制项目进度,项目经理需要做好以下工作
对于项目的管理者来说,项目信息透明,能够更容易让管理者发现项目中的问题,及时找到问题的原因和相关任务的责任人。 当项目信息能相对精准地呈现给管理者时,也能促进项目成员也能更加认真负责的完成任务,不会找借口推…...
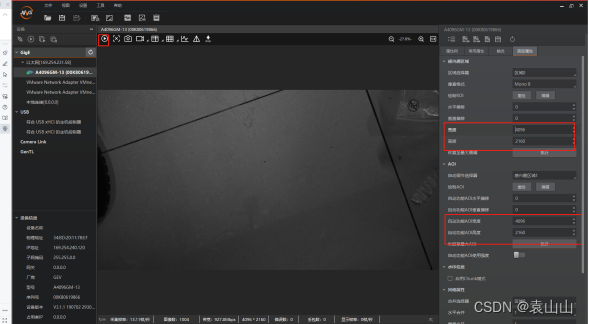
海康工业相机使用教程
工业相机使用一、硬件连接1、准备材料2、相机供电(1)区分电源适配器正负极(2)连接相机电源线缆(3)连接完成后,相机蓝色灯常亮则成功3、软件连接(1)MVS客户端下载地址&…...

java开发手册之安全规约
安全规约隶属于用户个人的页面或者功能必须进行权限控制校验。 说明:防止没有做水平权限校验就可随意访问、修改、删除别人的数据,比如查看他人的私信内容、修改他人的订单。 用户敏感数据禁止直接展示,必须对展示数据进行脱敏。 说明&#x…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
