蓝桥杯简单模板
目录
最大公约数
两个数的最大公约数
多个数的最大公约数
最小公倍数
两个数的最小公倍数
多个数的最小公倍数
素数
编辑
位数分离
正写
编辑
反写
闰年
最大公约数
两个数的最大公约数
之前看见的是辗转相除法,例如现在让算一个49,21的最大公约数
#include<iostream>
using namespace std;
int main()
{int a=49,b=21;while(b!=0){int tmp=b;b=a%b;a=tmp;}cout<<a;return 0;} 模拟一下过程
刚开始a=49,b=21,循环判断b不等于0,进入循环,tmp=21,b=a%b=49%21=7,a=tmp=21;
现在a=21,b=7,循环判断b不等于0,进入循环,tmp=7,b=a%b=21%7=0,a=tmp=7;
现在a=7,b=0,循环判断b不等于0,循环结束;
打印a=7;
加上过程的打印:
#include<iostream>
using namespace std;
int main()
{int a=49,b=21;cout<<"a="<<a<<",b="<<b<<endl;while(b!=0){int tmp=b;b=a%b;a=tmp;cout<<"a="<<a<<",b="<<b<<endl;}cout<<endl<<a;return 0;} 运行结果如下图:
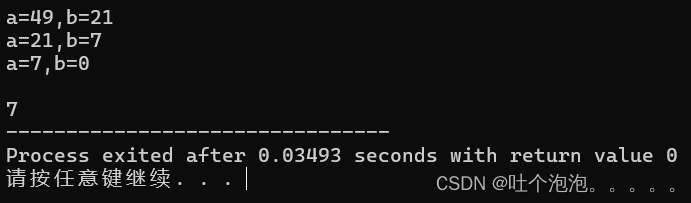
多个数的最大公约数
可以先把前两个数的最大公约数求出来之后,在依次和剩下的数进行辗转相除,求出一组数的最大公约数
#include<iostream>
using namespace std;
int gcd(int a,int b);
int gcd(int a,int b)
{while(b!=0){int tmp=b;b=a%b;a=tmp;}return a;
}
int main()
{int arr[4]={5,75,80,2000};int num=arr[0];for(int i=1;i<4;i++){num=gcd(num,arr[i]);}cout<<num;return 0;} 最小公倍数
两个数的最小公倍数
最小公倍数数的求法,一般是将两个数相乘,然后除两个数的最大公约数,下面是具体代码:
#include<iostream>
using namespace std;
int gcd(int a,int b)
{while(b!=0){int tmp=b;b=a%b;a=tmp;}return a;
}int main(){int a=21,b=7;cout<<a*b/gcd(a,b)<<endl;return 0;}多个数的最小公倍数
也是同求多个数的最大公约数一样,先求出前两个的最小公倍数,然后依次于剩下的数求出整个数组的最小公倍数。代码如下:
#include<iostream>
using namespace std;
int gcd(int a,int b);
int gcd(int a,int b)
{while(b!=0){int tmp=b;b=a%b;a=tmp;}return a;
}
int main()
{int arr[4]={50,100,10,20};int num=arr[0];for(int i=1;i<4;i++){num=num*arr[i]/gcd(num,arr[i]);}cout<<num;return 0;} 素数
因数只有1和他本身的数
#include<iostream>using namespace std;bool isprime(int n){for(int i=2;i*i<n;i++){if(n%i==0)return false;}return true;}int main(){for(int i=2;i<100;i++){if(isprime(i))printf("%d\t",i);}return 0;}结果如下
位数分离
有时候会给一些数,然后让分离每个位数的数字,有时候是正写,有时候是反写
正写
正写老师教过递归的写法,但是有些不熟练,我这里的方法是先统计这个数是几位数,然后依次除。
#include<iostream>
#include<cmath>
using namespace std;
int main()
{int a=12345678;int num=a;//用来统计位数int t=0;while(num) {num/=10;t++;}while(t){t--;int i=a/pow(10,t);a=a-i*pow(10,t);cout<<i<<' ';}return 0;} 结果如下
反写
根据模的特点
#include<iostream>using namespace std;int main(){int a=12345678;while(a){cout<<a%10<<' ';a/=10; }return 0;}结果如下

闰年
不是百年的时候,每四年一闰,
是百年的时候,四百年一闰
#include<iostream>
using namespace std;
bool leap(int year)
{if(year%400==0||year%100!=0&&year%4==0)return true;return false;}
int main()
{for(int i=1;i<1000;i++){if(leap(i))printf("%d\t",i);}return 0;
}结果

相关文章:

蓝桥杯简单模板
目录 最大公约数 两个数的最大公约数 多个数的最大公约数 最小公倍数 两个数的最小公倍数 多个数的最小公倍数 素数 编辑 位数分离 正写 编辑 反写 闰年 最大公约数 两个数的最大公约数 之前看见的是辗转相除法,例如现在让算一个49,21…...
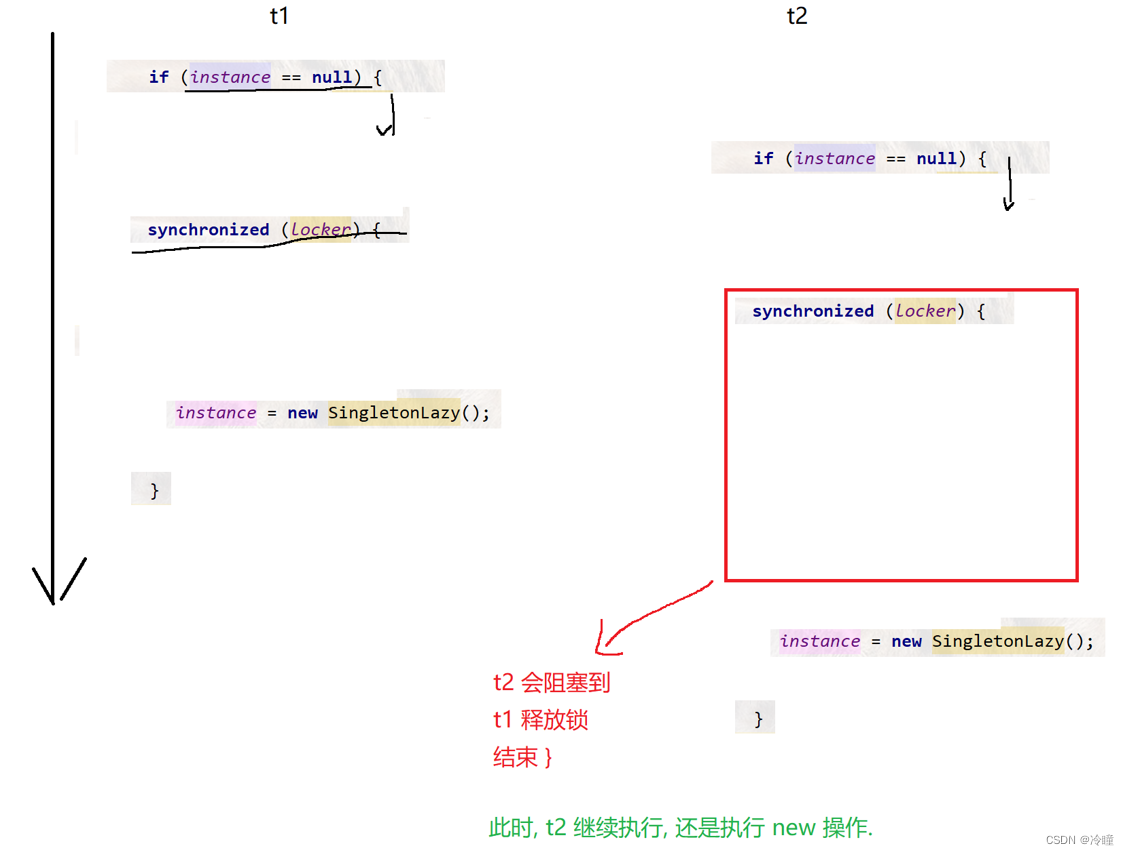
单例模式(饿汉模型,懒汉模型)
在着里我们先了解什么是单例模式。 就是某个类在进程中只能有单个实例,这里的单例模式需要一定的编程技巧,做出限制,一旦程序写的有问题,创建了多个实例,编程就会报错。 如果我们学会了单例模式,这种模式…...
torchvision中的数据集使用
torchvision中的数据集使用 使用和下载CIFAR10数据集 输出测试集中的第一个元素(输出img信息和target) 查看分类classes 打断点–>右键Debug–>找到classes 代码 import torchvisiontrain_set torchvision.datasets.CIFAR10(root"./data…...
linux 迁移home目录以及修改conda中pip的目录,修改pip安装路径
1)sudo rsync -av /home/lrf /data/home/lrf 将/home目录下的文件进行复制(假设机械硬盘挂载在/data目录下)** 2)usermod -d /data/home/lrf -m lrf 修改用户$HOME变量** 3)vi /etc/passwd 查看对应用户的$HOME变量是…...
解析大语言模型训练三阶段
大语言模型的训练过程一般包括3个阶段:预训练(Pre-training)、SFT(有监督的微调,Supervised-Finetuning)以及RLHF(基于人类反馈的强化学习,Reinforcement Learning from Human Feedb…...

知识图谱的最新进展与未来趋势
知识图谱的最新进展与未来趋势 一、引言 在过去的几年中,知识图谱已经从一个前沿的研究概念发展成为现代信息技术不可或缺的一部分。作为结构化知识的存储和表示形式,知识图谱通过组织信息和数据提供了深刻的洞见,它已被广泛应用于搜索引擎优…...
Facebook直播延迟过高是为什么?
在进行Facebook直播 时,高延迟可能会成为一个显著的问题,影响观众的观看体验和互动效果。以下是一些导致Facebook直播延迟过高的可能原因: 1、网络连接问题 网络连接不稳定或带宽不足可能是导致Facebook直播延迟的主要原因之一。如果您的网络…...

CentOS 7.9 额外安装一个Python3.x版本详细教程
Centos7默认的python版本是2.7,根据需要我们额外安装一个Python3.x版本。 1、安装基础环境 yum update -yyum -y groupinstall "Development tools"yum install openssl-devel bzip2-devel expat-devel gdbm-devel readline-devel sqlite-devel psmisc …...

uml时序图中,消息箭头和消息调用箭头有什么区别
在UML时序图中,消息箭头和消息调用箭头是用来表示不同类型的消息传递关系的符号。 1. 消息箭头:消息箭头用来表示消息在不同对象之间的传递,通常是实例方法之间的调用关系。消息箭头从消息发送者指向消息接收者,表示消息的传递方…...

12.C++常用的算法_遍历算法
文章目录 遍历算法1. for_each()代码工程运行结果 2. transform()代码工程运行结果 3. find()代码工程运行结果 遍历算法 1. for_each() 有两种方式: 1.普通函数 2.仿函数 代码工程 #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<vect…...
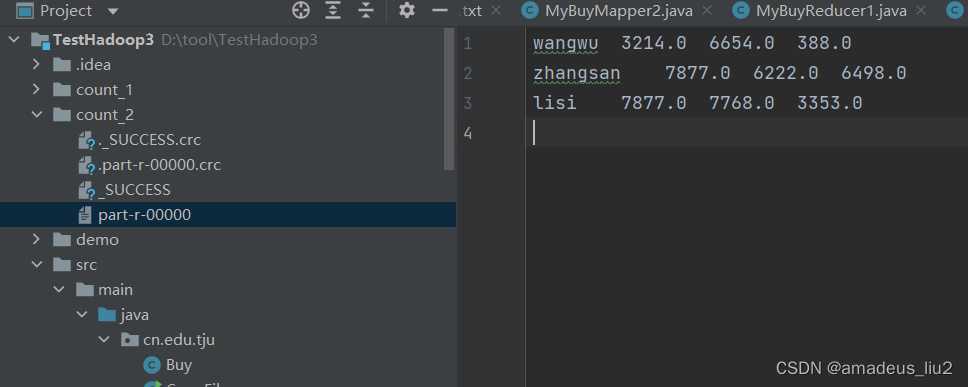
hadoop:案例:将顾客在京东、淘宝、多点三家平台的消费金额汇总,然后先按京东消费额排序,再按淘宝消费额排序
一、原始消费数据buy.txt zhangsan 5676 2765 887 lisi 6754 3234 1232 wangwu 3214 6654 388 lisi 1123 4534 2121 zhangsan 982 3421 5566 zhangsan 1219 36 45二、实现思路:先通过一个MapReduce将顾客的消费金额进行汇总,再通过一个MapReduce来根据金…...
)
2024年华为OD机试真题-孙悟空吃蟠桃-Python-OD统一考试(C卷)
题目描述: 孙悟空爱吃蟠桃,有一天趁着蟠桃园守卫不在来偷吃。已知蟠桃园有N颗桃树,每颗树上都有桃子,守卫将在H小时后回来。 孙悟空可以决定他吃蟠桃的速度K(个/小时),每个小时选一颗桃树,并从树上吃掉K个,如果树上的桃子少于K个,则全部吃掉,并且这一小时剩余的时间…...

vue3 开发中遇到的问题
1. element-plus的el-popover内置el-select组件,如何避免关闭el-popover 在el-select内置上面添加:teleported"false"就可以避免在点击el-select时候,把el-popver给关闭了 2. validate-on-rule-change:是否在 rules 属性改变后…...
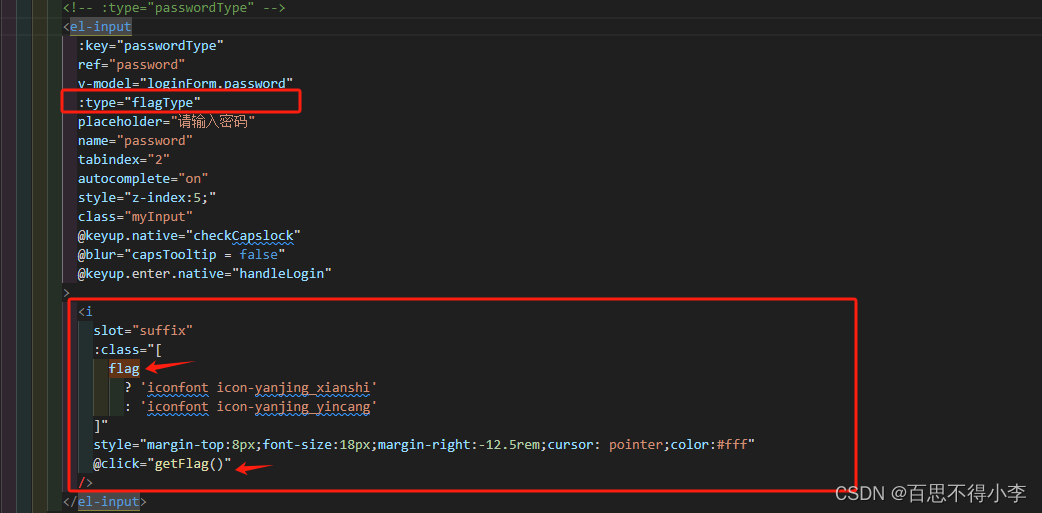
Vue input密码输入框自定义密码眼睛icon
我们用的饿了么UI组件库里,密码输入框的icon是固定不变的,如下所示: 点击"眼睛"这个icon不变,现在需求是UI给的设计稿里,密码输入框的"眼睛"有如下两种: 代码如下: <el-input:key="passwordType"ref="password"...

【LAMMPS学习】八、基本知识的讨论(1.4)多副本模拟
8. 基本知识的讨论 此部分描述了如何使用 LAMMPS 为用户和开发人员执行各种任务。术语表页面还列出了 MD 术语,以及相应 LAMMPS 手册页的链接。 LAMMPS 源代码分发的 examples 目录中包含的示例输入脚本以及示例脚本页面上突出显示的示例输入脚本还展示了如何设置和…...
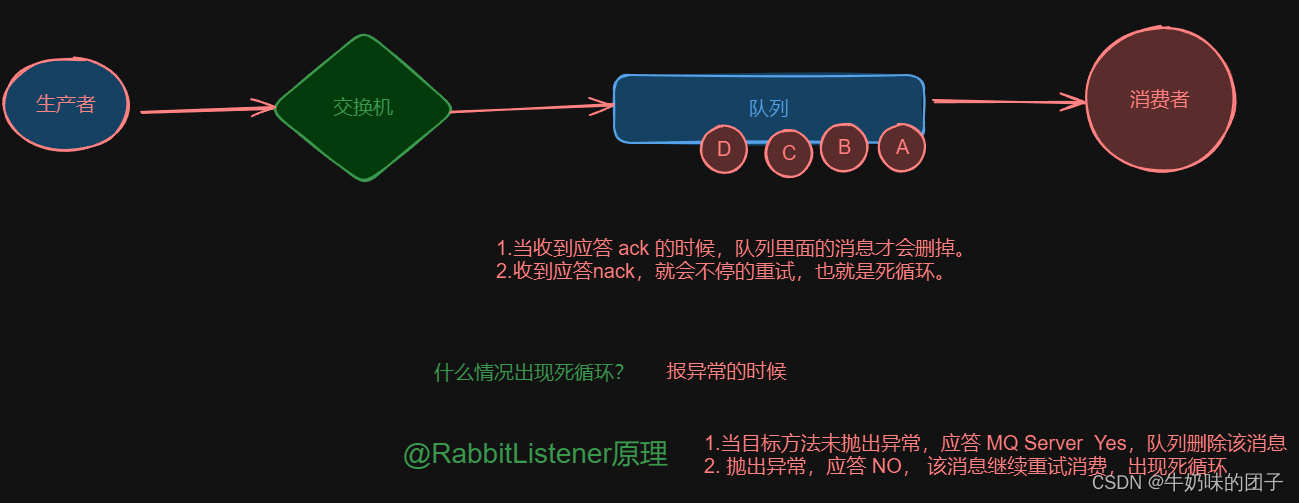
SpringBoot整合RabbitMQ-应答模式
一、应答模式 RabbitMQ 中的消息应答模式主要包括两种:自动应答(Automatic Acknowledgement)和手动应答(Manual Acknowledgement)。(一般交换机发送消息,RabbitMQ只有在接收到消费者的确认后才…...

51单片机入门_江协科技_25~26_OB记录的笔记_蜂鸣器教程
25. 蜂鸣器 25.1. 蜂鸣器介绍 •蜂鸣器是一种将电信号转换为声音信号的器件,常用来产生设备的按键音、报警音等提示信号 •蜂鸣器按驱动方式可分为有源蜂鸣器和无源蜂鸣器(开发板上用的无源蜂鸣器) •有源蜂鸣器:内部自带振荡源&a…...

新能源汽车电池包为什么不通用,车主怎么用电才算对?
一提起新能源车,大部分人可能知道电动汽车,实际上新能源车的种类是比较多的,这里边也包括了插电式混动汽车、纯电汽车、燃料电池汽车,其中插电混动里还包括了串联式、并联式、混联式,每种汽车都各有优缺点,…...

[C语言]——柔性数组
目录 一.柔性数组的特点 二.柔性数组的使用 三.柔性数组的优势 C99中,结构体中的最后⼀个元素允许是未知大小的数组,这就叫做『柔性数组』成员。 typedef struct st_type //typedef可以不写 { int i;int a[0];//柔性数组成员 }type_a; 有些编译器会…...

密码学 总结
群 环 域 群 group G是一个集合,在此集合上定义代数运算*,若满足下列公理,则称G为群。 1.封闭性 a ∈ G , b ∈ G a\in G,b\in G a∈G,b∈G> a ∗ b ∈ G a*b\in G a∗b∈G 2.G中有恒等元素e,使得任何元素与e运算均为元素本…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...