密码学 总结
群 环 域
群 group
G是一个集合,在此集合上定义代数运算*,若满足下列公理,则称G为群。
1.封闭性 a ∈ G , b ∈ G a\in G,b\in G a∈G,b∈G=> a ∗ b ∈ G a*b\in G a∗b∈G
2.G中有恒等元素e,使得任何元素与e运算均为元素本身(如:单位矩阵、加法的0,乘法的1)
3.G的每个非0元素都有逆元素,使得元素*逆元素=e(如:加法中的负数,乘法中的倒数)
4.满足结合律
阿贝尔群(可交换群):
1.满足群的四条公理
2.满足交换律(矩阵不满足)
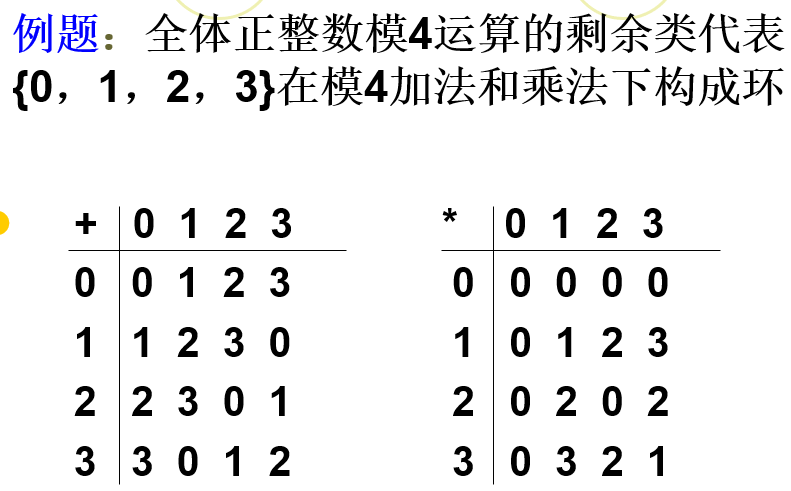
例:(7,3)码在模2加法下构成群,(n,k)码又称群码
0000000 单位元
0011101
0100111
0111010
1001110
1010011
1101001
1110100
封闭性可验证。存在e。每个元素的逆都是他们本身。模2加法相当于异或,满足结合律。故此运算为群。
线性分组编码
环 Ring
R是一个集合,在其上定义两种代数运算+、*,若满足下列公理则称为环
1.+下构成群
2.*下满足封闭性
3. *下满足结合律
4. 分配律成立(包括左分配和右分配)
左分配:a(b+c)=ab+ac
右分配:(b+c)a=ba+ca
如:矩阵的乘对加满足分配律
e.g.
整数集合是环,加法和乘法构成整数环
实系数的多项式环
域 Field
在F集合上定义两种代数运算+和*,若满足下列公理,则F称为域
1.在加法下构成群
2.全体非0元素构成交换乘群(=加法和乘法都成群)
3.对加法和乘法分配律成立
域是有单位元素、非0元素有逆元素的交换环
e,g,以p=3为模的剩余类全体{0,1,2}构成域
有限域:域中元素数目是有限的; 记为: GF(q)q为域的阶,称为q元域;
无限域:域中元素的数目是无限的;
域的阶:域中元素的数目;
GF(2)为二元域,是最小的域
实际应用中,q的量级是 2 1024 2^{1024} 21024,非常巨大
数域包括 复数域、实数域、有理数域
二元域上的多项式
系数取自GF(2),含有一个未定元x的多项式称为GF(2)上的多项式,用f(x)表示。
多项式的加法:同幂次的系数相加
多项式的乘法:正常展开
相加时使用模2加法,即异或,即不进位的加法
x 2 − x = x 2 + ( 1 ) − 1 x = x 2 + x x^2-x=x^2+(1)^{-1}x=x^2+x x2−x=x2+(1)−1x=x2+x
二元域上的既约多项式
f(x)是次数>0的多项式,若除了1和多项式本身以外,不能再被GF(2)上的其他多项式除尽,则称为f(x)是二元域上的既约多项式(不可约多项式)。
即,不能分解为两个多项式的乘积
e.g.m=4,f(x)= x 4 + x + 1 x^4+x+1 x4+x+1 等价于五元向量(1,0,0,1,1)
f(x)不能在GF(2)上分解,但可以在更大的范围域内分解
定义:如果有两个域F1,F2,如果 F 1 ⊂ F 2 F_1\subset F_2 F1⊂F2,则F2是F1的扩域。
在域F1上的一个不可约多项式,在其扩域F2上可能有根,如果f(x)在F2上有根 α \alpha α,则在F2上f(x)有分解因子 ( x − α ) (x-\alpha ) (x−α)
e.g. x 2 + 1 x^2+1 x2+1在R内不可分解,但在复数域上可以分解为(x+i)(x-i)
设P(x)是GF(2)上的m次既约多项式,GF(2)上所有次数小于m的多项式的全体,在模2加法、模P(x)乘法运算下构成一个 2 m 2^m 2m阶的有限域,称为GF( 2 m 2^m 2m),GF(2)是扩域GF( 2 m 2^m 2m)的基域。扩域GF( 2 m 2^m 2m)中有 2 m 2^m 2m个元素,每个元素形如: a m − 1 x m − 1 + a m − 2 x m − 2 + . . . + a 1 x + a 0 a_{m-1}x^{m-1}+a_{m-2}x^{m-2}+...+a_1x+a_0 am−1xm−1+am−2xm−2+...+a1x+a0,可记为m维二元向量的形式( a m − 1 , a m − 2 , . . . , a 1 , a 0 a_{m-1},a_{m-2},...,a_1,a_0 am−1,am−2,...,a1,a0)
设P(x)是GF(2)上的一个m次既约多项式,如果构成的扩域GF( 2 m 2^m 2m)中的全体非0多项式元素对模P(x)乘法构成乘法循环群,即,存在GF( 2 m 2^m 2m)的一个非0元素 α ∈ G F ( 2 m ) \alpha \in GF(2^m) α∈GF(2m),它的各次幂 α 0 , α 1 , . . . , α 2 m − 2 \alpha ^0,\alpha ^1,...,\alpha ^{2^m-2} α0,α1,...,α2m−2恰好构成扩域GF( 2 m 2^m 2m)的全部非零元素,则称P(x)是GF(2)上的一个m次本原多项式。有:
1. α \alpha α是GF(2)的一个本原元
2. α \alpha α是GF(2)上的既约多项式P(x)在扩域GF( 2 m 2^m 2m)中的一个根
3.GF(2)上的本原多项式P(x)在扩域GF( 2 m 2^m 2m)中的任何一个根都是本原元
e.g.

( 0 , 1 , α , α 2 , . . . . , α 14 ) (0,1,\alpha,\alpha^2,....,\alpha^{14}) (0,1,α,α2,....,α14)构成域,称为GF(2)的4次扩域。域的阶为16,记为GF( 2 4 2^4 24)。也构成循环群。
求逆:扩展欧几里得算法
对称加密算法 AES
AES(Advanced Encryption Standard) 之 Rijndael算法
迭代分组密码,分组长度为128b,密码长度为128/192/256b,相应的轮数r为10/12/14
讨论密钥长度为128b,分组长度为128b的情况
128b的消息被分为16个字节,每字节8位,记为InputBlock=m0,m1,m2…m15
密钥分组如下:InputKey=k0,k1,k2…k15
内部数据结构表示为一个4x4的矩阵:
I n p u t B l o c k = [ m 0 m 4 m 8 m 12 m 1 m 5 m 9 m 13 m 2 m 6 m 10 m 14 m 3 m 7 m 11 m 15 ] InputBlock=\begin{bmatrix} m0& m4& m8& m12\\ m1& m5& m9& m13\\ m2& m6& m10& m14\\ m3& m7& m11& m15 \end{bmatrix} InputBlock= m0m1m2m3m4m5m6m7m8m9m10m11m12m13m14m15
I n p u t K e y = [ k 0 k 4 k 8 k 12 k 1 k 5 k 9 k 13 k 2 k 6 k 10 k 14 k 3 k 7 k 11 k 15 ] InputKey=\begin{bmatrix} k0& k4& k8& k12\\ k1& k5& k9& k13\\ k2& k6& k10& k14\\ k3& k7& k11& k15 \end{bmatrix} InputKey= k0k1k2k3k4k5k6k7k8k9k10k11k12k13k14k15
轮变换
Round(State,RoundKey)
State是轮消息矩阵,被看作输入和输出,RoundKey是轮密钥矩阵,由输入密钥通过密钥表导出,一轮的完成将导致State的元素改变状态。
每轮变换由四个不同的变换组成:
SubBytes(State)
模f(x)= x 8 + x 4 + x 3 + x + 1 x^8+x^4+x^3+x+1 x8+x4+x3+x+1得到扩域GF( 2 8 2^8 28),有256个元素。
SubBytes函数为State的每个字节(x)提供非线性变换,任一非0的字节x ∈ F 2 8 \in F_{2^8} ∈F28被下面的变换取代: y = A x − 1 + b y=Ax^{-1}+b y=Ax−1+b 。求逆体现了变换的非线性,A是可逆的,所以此变换可逆。

e.g.
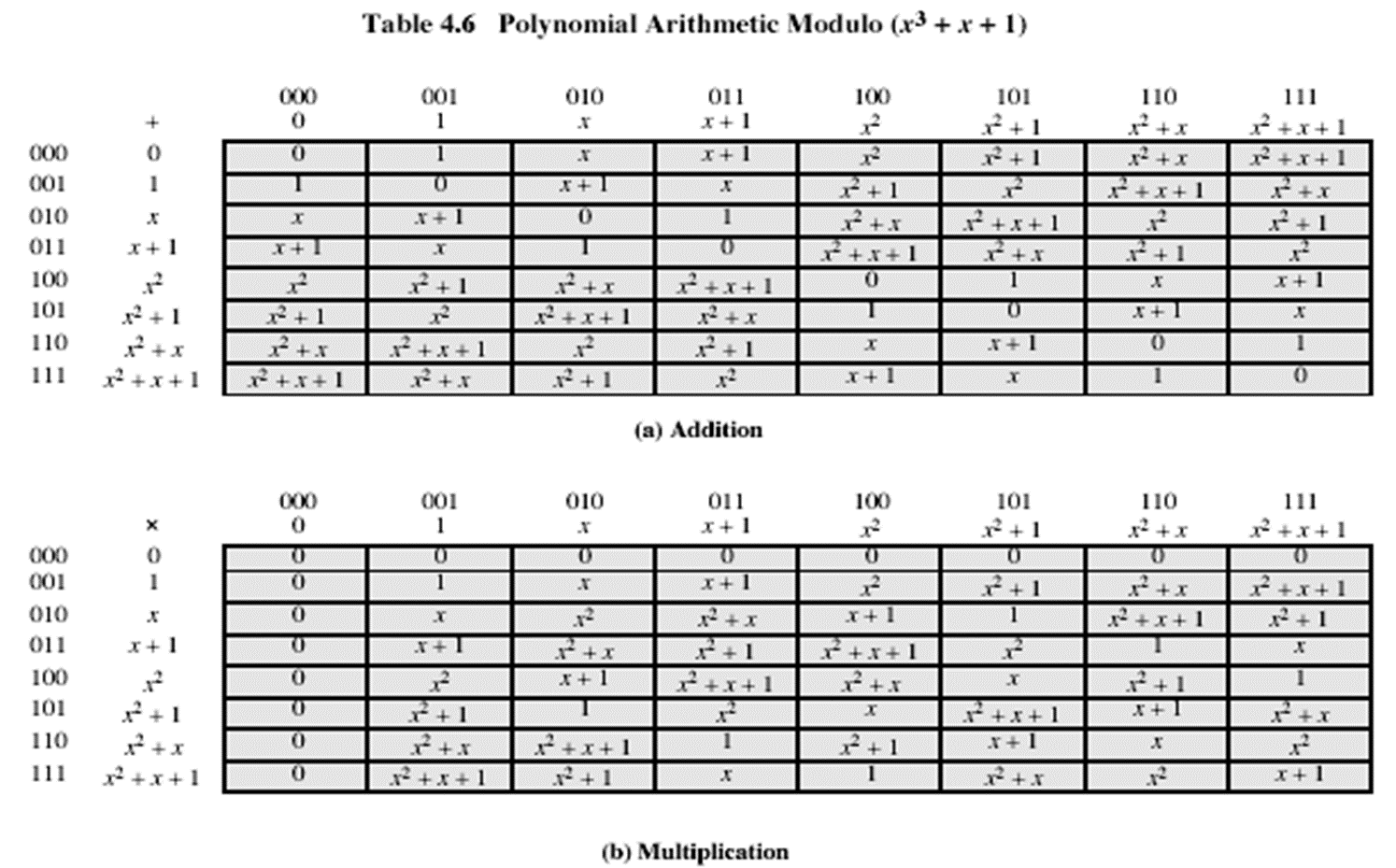
由于系数是0或1,因此可以将任何这样的多项式表示为比特串
加法是这些位串的XOR
乘法是移位&XOR
通过用不可约多项式的余数重复替换最高幂来实现模约简(也称为移位和XOR)
ShiftRows(State)

每行分别循环左移0,1,2,3位
MixColumns(State)
这个函数对State的每一列作用,迭代四次,下面仅仅描述对一列的作用:
令State的一列为: [ S 0 S 1 S 2 S 3 ] \begin{bmatrix} S_0\\ S_1\\ S_2\\ S_3 \end{bmatrix} S0S1S2S3 ,把这一列表示为三次多项式: s ( x ) = s 3 x 3 + s 2 x 2 + s 1 x + s 0 s(x)=s_3x^3+s_2x^2+s_1x+s_0 s(x)=s3x3+s2x2+s1x+s0,因为s(x)的系数是字节,也就是说是 F 2 8 F_2^8 F28域中的元素,所以这个多项式是 F 2 8 F_2^8 F28上的。
列s(x)上的运算定义为将这个多项式乘以一个固定的3次多项式c(x),然后模x4+1:
d ( x ) = c ( x ) × s ( x ) ( m o d x 4 + 1 ) d(x) = c(x) × s(x) (mod \ x^4+1) d(x)=c(x)×s(x)(mod x4+1)
c ( x ) = c 3 x 3 + c 2 x 2 + c 1 x + c 0 c(x)=c_3x^3+c_2x^2+c_1x+c_0 c(x)=c3x3+c2x2+c1x+c0
其中, x i ( m o d x 4 + 1 ) = x i m o d 4 x^i(mod \ x^4+1)=x^{imod4} xi(mod x4+1)=ximod4
Rijndeal给出:c3=“03”, c2=“01”, c1=“01”, c0=“02”
在乘积d(x)中,x2的系数是d2=c2s0+c1s1+c0s2+c3s3
上述乘法的系数可以写成以下矩阵乘法: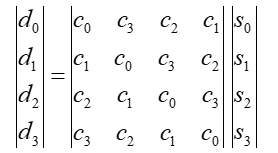
F 8 F_8 F8上,c(x)与 x 4 + 1 x^4+1 x4+1是互素的,所以在 F 8 ( x ) F_8(x) F8(x)中,逆 c ( x ) − 1 ( m o d x 4 + 1 ) c(x)^{-1} (modx^4+1) c(x)−1(modx4+1)是存在的。这等于说,上述矩阵变换是可逆的。
AddRoundKey(State, RoundKey)
这个函数是逐字节、逐比特地将RoundKey中的元素与State中的元素相加。这里的加,是F2中的加,也就是异或运算,是平凡可逆的。
不同轮的密钥比特是不同的。它们使用一个固定的“密钥表”导出密钥,每轮密钥不同,该“密钥表”是非秘密的。具体细节可参阅有关NIST的标准文件。
解密
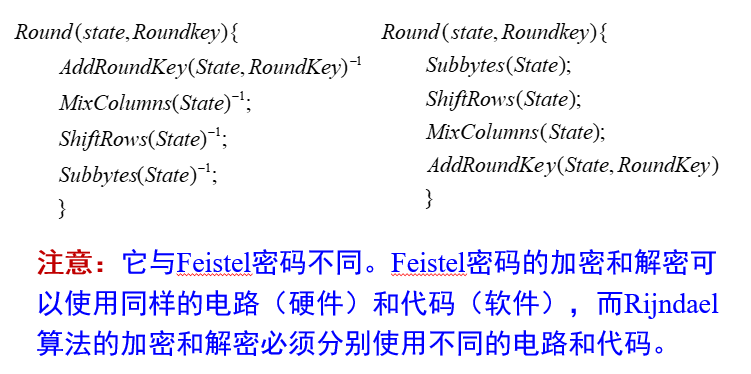
非对称加密算法 RSA
非对称,指的是加密和解密的密钥不同,又称双钥密码技术、公钥密码技术。
当密钥足够长(现在常用1024bit以上)时,破解极其困难。
特点
公钥可以公布,私钥不可公布。
由私钥可以容易计算出公钥,反之困难。
陷门单向函数
若函数f:A->B可逆(单射+满射),且满足对 x ∈ A x\in A x∈A,易于求解f(x),但由f(x)求x极为困难,则称为 单向函数。
陷门单项函数:
f z : A z − > B z , z ∈ Z f_z:A_z->B_z,z\in Z fz:Az−>Bz,z∈Z,Z是陷门信息集合。
1)在给定 z ∈ Z z\in Z z∈Z下容易找到一对算法 E z E_z Ez和 D z D_z Dz,使得对所有 x ∈ A x\in A x∈A,易于计算 f z f_z fz及其逆,即: f z ( x ) = E z ( x ) , D z ( f z ( x ) ) = x f_z(x)=E_z(x),D_z(f_z(x))=x fz(x)=Ez(x),Dz(fz(x))=x。
2)只给定 E z E_z Ez和 D z D_z Dz时,对所有 x ∈ A x\in A x∈A都很难从 y = f z ( x ) y=f_z(x) y=fz(x)中计算出x
单向函数是求逆困难的函数,而陷门单项函数是在不知道陷门信息下求逆困难、在知道陷门信息下求逆容易的函数。
用于构造双钥密码的单向函数
-
多项式求根
有限域GF§上的多项式 y = f ( x ) = ( x n + a n − 1 x n − 1 + . . . + a 1 x + a 0 ) m o d p y=f(x)=(x^n+a_{n-1}x^{n-1}+...+a_1x+a_0)mod \ p y=f(x)=(xn+an−1xn−1+...+a1x+a0)mod p,当给定a,x,p后,很容易求出f(x),但已知a,y,p,想求x非常困难,n,p很大时几乎无法求解。 -
离散对数DL
p是大素数,a是{0,1,2…,p-1}中与p互素的数。
已知p,a,x,求f(x)= a x m o d p a^xmod\ p axmod p很容易,但已知p,a,f(x),求x(离散对数)很困难,计算时间是指数级 -
大整数分解FAC
已知大素数p,q,求n=pq只需一次乘法,但已知n求pq非常困难,已知算法有:
试除法、二次筛、数域筛、椭圆曲线。
给定n求pq的问题称为rsa问题。求n=pq分解的问题与以下几个问题等价:
1)给定m,c,n,求d使得 c d = m m o d n c^d=m\ mod\ n cd=m mod n
2)给定k,c,n,求m使得 m k = c m o d n m^k=c \ mod\ n mk=c mod n
3)给定x,m,求是否存在y使得 x = y 2 m o d m x=y^2\ mod\ m x=y2 mod m(二次剩余问题) -
背包问题
-
菲-赫尔曼问题 DHP
给定素数p,可构造一乘群 Z p ∗ = { 1 , 2 , . . . p − 1 } Z^*_p=\{1,2,...p-1\} Zp∗={1,2,...p−1},令a为Z的生成元,若已知 a a , a b a^a,a^b aa,ab,求 a a b a^{ab} aab -
二次剩余问题QR
给定奇合数n和整数a,决定a是否为mod n的平方剩余 -
模n的平方问题 SQROOT
RSA算法
安全性依赖于大整数分解的难度
n = p q , φ ( n ) = ( p − 1 ) ( q − 1 ) n=pq,\varphi(n)=(p-1)(q-1) n=pq,φ(n)=(p−1)(q−1)为欧拉函数
公钥为e,满足 ( e , φ ( n ) ) = 1 (e,\varphi(n))=1 (e,φ(n))=1,私钥为d, d = e − 1 m o d φ ( n ) d=e^{-1}mod\ \varphi(n) d=e−1mod φ(n)
加密:m->c= m e m o d n m^emod\ n memod n
解密:c->m= c d m o d n c^dmod\ n cdmod n
也就是找三个大素数p,q,e,求出 d = e − 1 m o d φ ( n ) d=e^{-1}mod \varphi(n) d=e−1modφ(n),求逆的方法是扩展欧几里得算法。
公钥是n,e,密钥是d,公钥可公开,密钥不可公开, φ ( n ) , p , q \varphi(n),p,q φ(n),p,q都应该销毁。
用途
加密:A->用B的公钥加密->密文->用B的私钥解密->B,常用于交换对称加密算法的密钥,因为加密解密速度较慢。
数字签名:A->用A的私钥加密->签名->用A的公钥解密->B 得以验证


相关文章:

密码学 总结
群 环 域 群 group G是一个集合,在此集合上定义代数运算*,若满足下列公理,则称G为群。 1.封闭性 a ∈ G , b ∈ G a\in G,b\in G a∈G,b∈G> a ∗ b ∈ G a*b\in G a∗b∈G 2.G中有恒等元素e,使得任何元素与e运算均为元素本…...
尚硅谷html5+css3(1)html相关知识
1.基本标签: <h1>最大的标题字号 <h2>二号标题字号 <p>换行 2.根标签<html> 包括<head>和<body> <html><head><title>title</title><body>body</body></head> </html> 3…...
苍穹外卖11(Apache ECharts前端统计,营业额统计,用户统计,订单统计,销量排名Top10)
目录 一、Apache ECharts【前端】 1. 介绍 2. 入门案例 二、营业额统计 1. 需求分析和设计 1 产品原型 2 业务规则 3 接口设计 2. 代码开发 3. 功能测试 三、用户统计 1. 需求分析和设计 1 产品原型 2 业务规则 3 接口设计 2. 代码开发 3. 功能测试 四、订单统…...
大商创多用户商城系统 多处SQL注入漏洞复现
0x01 产品简介 大商创多用户商城系统是一个功能强大、灵活多变的新零售电商系统服务商。该系统支持平台自营和商家入驻,实现多元化经营模式,能够全面整合供应商、生产商、经销商和消费者等产业链资源,提高产品多样性,加快资金流动速度,并有助于减少不必要的成本输出。 0…...

美团一面4/9
面的时候自我感觉良好,复盘感觉答的一坨。。 0怎么比较两个对象 0Integer 不使用new会自动装箱,返回提前创建的。使用new就创建新对象。 1.Object类有什么方法 java中Object类中有哪些常用方法以及作用_java中object的方法有什么用-CSDN博客 2.hash…...
ubuntu下NTFS分区无法访问挂载-解决办法!
Ubuntu系统下,有的时候发现,挂载的NTFS文件系统硬盘无法访问。点击弹出类似问题: Error mounting /dev/sda1 at /media/root/新加卷: Command-line mount -t "ntfs" -o "uhelperudisks2,nodev,nosuid,uid0,gid0" "/…...

如何在 Ubuntu 14.04 上使用 Rsyslog、Logstash 和 Elasticsearch 实现日志集中管理
Elastic 的一篇文章 介绍 理解组织生成的数百万条日志行可能是一个艰巨的挑战。一方面,这些日志行提供了对应用程序性能、服务器性能指标和安全性的视图。另一方面,日志管理和分析可能非常耗时,这可能会阻碍对这些日益必要的服务的采用。 …...

mapbox 工作问题暂时记录
mapbox 工作问题暂时记录 mapbox样式修改1.2.3.4. mapbox样式修改 1. mapbox直接用class名无法修改样式, 可以添加 :deep 来修改样式 2. map.value.getStyle().layers这行代码可以获取页面中所有图层,可以判断图层id来做相应操作 3. map.value.setLayoutProperty(layer.id…...
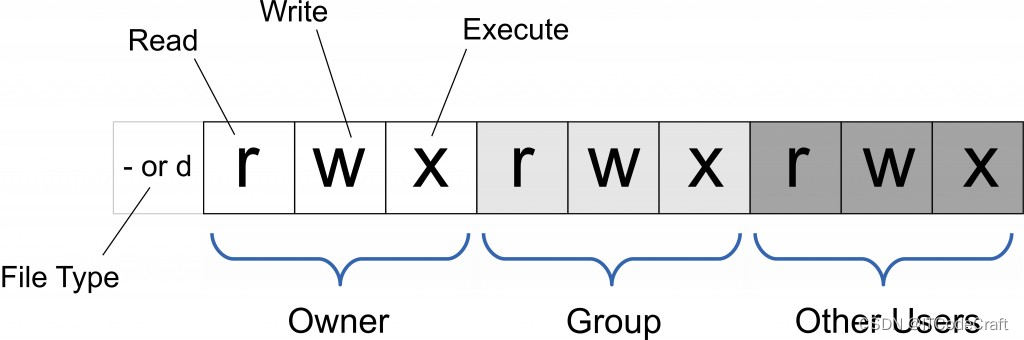
Linux、Docker、Brew、Nginx常用命令
Linux、Docker、Brew、Nginx常用命令 Linuxvi编辑器文件操作文件夹操作磁盘操作 DockerBrewNginx参考 Linux vi编辑器 Vi有三种模式。命令模式、输入模式、尾行模式,简单的关系如下: i -- 切换到输入模式,在光标当前位置开始输入文本。&a…...
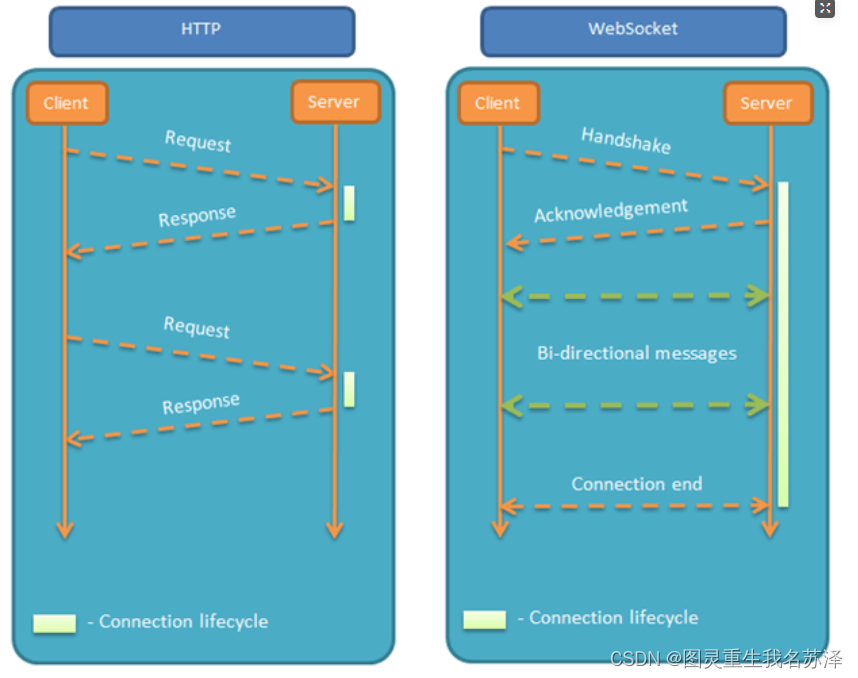
【Spring实战项目】SpringBoot3整合WebSocket+拦截器实现登录验证!从原理到实战
🎉🎉欢迎光临,终于等到你啦🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟持续更新的专栏《Spring 狂野之旅:从入门到入魔》 &a…...

第二证券|政策利好不断,工业母机概念爆发,华东数控等涨停
工业母机概念10日盘中大幅走高,截至发稿,恒进感应、宏德股份、华东重机、华东数控等涨停,凯腾精工涨超20%,创世纪涨逾11%,华辰配备、盘古智能涨超9%,博亚精工涨逾8%。 音讯面上,工业和信息化部…...
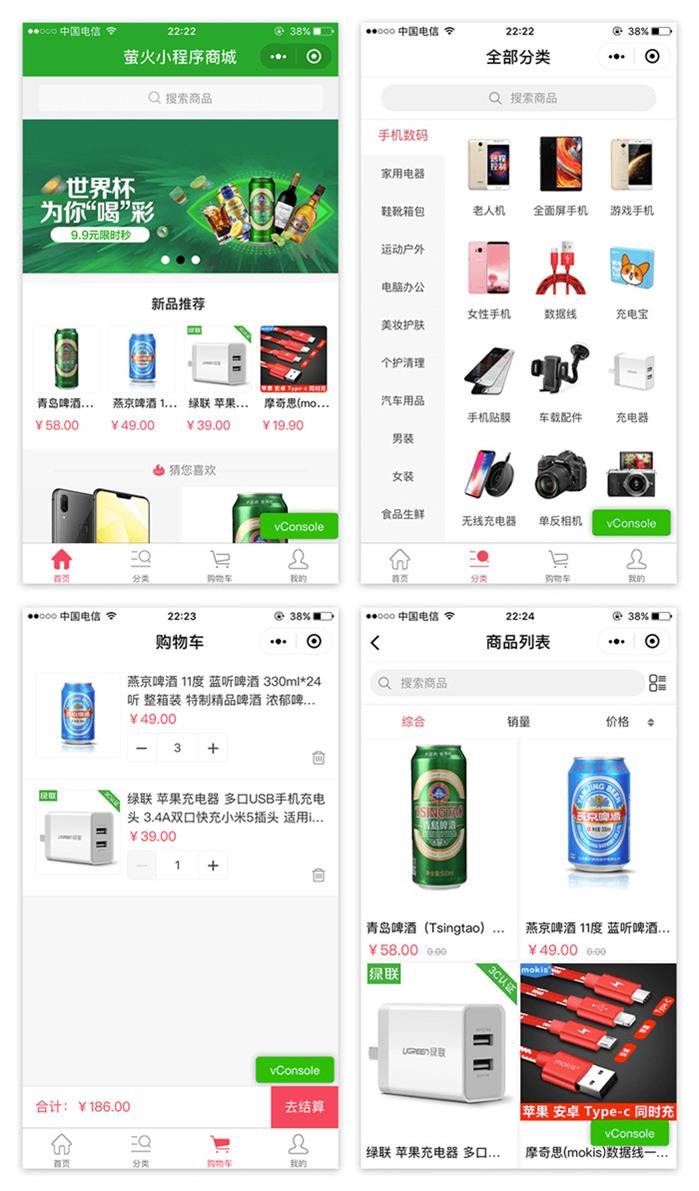
Thinkphp5萤火商城B2C小程序源码
源码介绍 Thinkphp5萤火商城B2C小程序源码,是一款开源的电商系统,为中小企业提供最佳的新零售解决方案。采用稳定的MVC框架开发,执行效率、扩展性、稳定性值得信赖。 环境要求 Nginx/Apache/IIS PHP5.4 MySQL5.1 建议使用环境ÿ…...

PostgreSQL介绍
PostgreSQL是一个高度先进的对象关系型数据库管理系(ORDBMS),其起源可以追溯到1986年,最初是加州大学伯克利分校计算机系的一个项目,名为POSTGRES。它是从Ingres项目演变而来的,目的是克服当时关系数据库系…...

简析数据安全保护策略中的十个核心要素
数据显示,全球企业组织每年在数据安全防护上投入的资金已经超过千亿美元,但数据安全威胁态势依然严峻,其原因在于企业将更多资源投入到数据安全能力建设时,却忽视了这些工作本身的科学性与合理性。因此,企业在实施数据…...

Python+Django+Html河道垃圾识别网页系统
程序示例精选 PythonDjangoHtml河道垃圾识别网页系统 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《PythonDjangoHtml河道垃圾识别网页系统》编写代码,代码整洁,规…...

BUUCTF:BUU UPLOAD COURSE 1[WriteUP]
构造一句话PHP木马 <?php eval(system($_POST[shell])); ?> 利用eval函数解析$shell的值使得服务器执行system命令 eval函数是无法直接执行命令的,只能把字符串当作php代码解析 这里我们构造的木马是POST的方式上传,那就用MaxHacKBar来执行 …...

从零开始学习:如何使用Selenium和Python进行自动化测试?
安装selenium 打开命令控制符输入:pip install -U selenium 火狐浏览器安装firebug:www.firebug.com,调试所有网站语言,调试功能 Selenium IDE 是嵌入到Firefox 浏览器中的一个插件,实现简单的浏览器操 作的录制与回…...
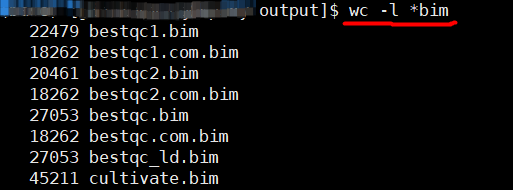
【linux基础】bash脚本的学习:定义变量及引用变量、统计目标目录下所有文件行数、列数
假设目的:统计并输出指定文件夹下所有文件行数 单个文件可以用 wc -l ;多个文件,可以用通配符 / 借助bash脚本 1.定义变量名,使用引号 a"bestqc.com.map" b"Anno.variant_function" c"enrichment/GOe…...

算法四十天-删除排序链表中的重复元素
删除排序链表中的重复元素 题目要求 解题思路 一次遍历 由于给定的链表是排好序的,因此重复的元素在链表中的出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。 具体地,我们从指针cur指向链表的头节…...

Linux-等待子进程
参考资料:《Linux环境编程:从应用到内核》 僵尸进程 进程退出时会进行内核清理,基本就是释放进程所有的资源,这些资源包括内存资源、文件资源、信号量资源、共享内存资源,或者引用计数减一,或者彻底释放。…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
