数据结构—堆
什么是堆
堆是一种特殊的树形结构,其中每个节点都有一个值。堆可以分为两种类型:最大堆和最小堆。在最大堆中,每个节点的值都大于等于其子节点的值;而在最小堆中,每个节点的值都小于等于其子节点的值。这种特性使得堆可以很方便地进行排序和提取最值等操作。如下图所示,左边这个图是最小堆,右边这个图是最大堆。

堆的用途
当我们只关心所有数据中的最大值或者最小值,存在多次获取最大值或者最小值,多次插入或删除数据时,就可以使用堆。
有小伙伴可能会想到用有序数组,初始化一个有序数组时间复杂度是 O(nlog(n)),查找最大值或者最小值时间复杂度都是 O(1),但是,涉及到更新(插入或删除)数据时,时间复杂度为 O(n),即使是使用复杂度为 O(log(n)) 的二分法找到要插入或者删除的数据,在移动数据时也需要 O(n) 的时间复杂度。
相对于有序数组而言,堆的主要优势在于插入和删除数据效率较高。 因为堆是基于完全二叉树实现的,所以在插入和删除数据时,只需要在二叉树中上下移动节点,时间复杂度为 O(log(n)),相比有序数组的 O(n),效率更高。
不过,需要注意的是:Heap 初始化的时间复杂度为 O(n),而非 O(nlogn)。
堆的存储
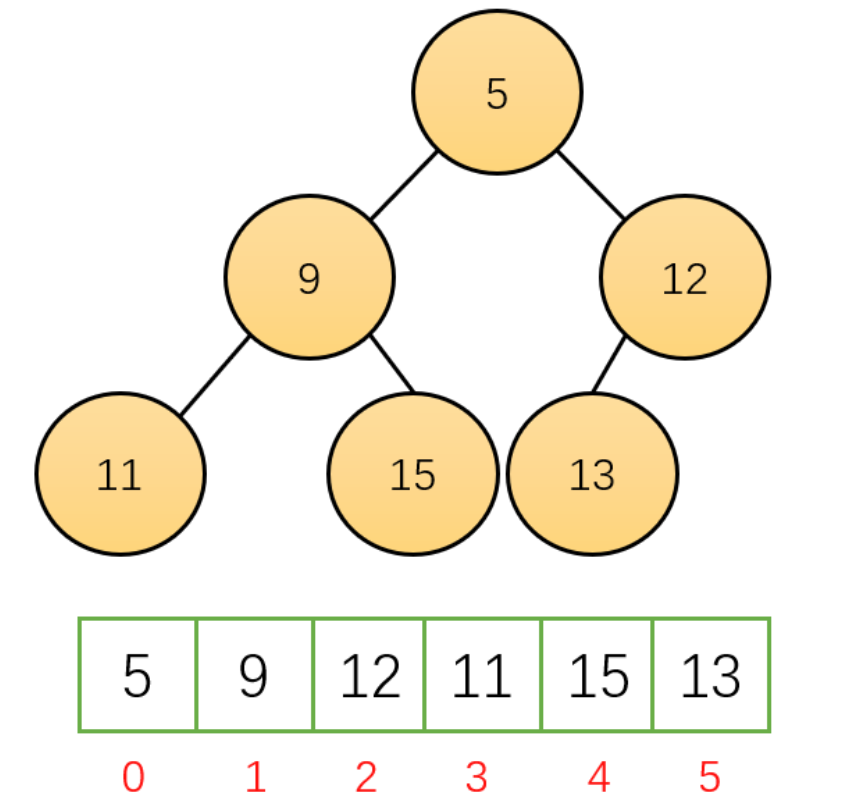
在介绍树的时候说过,由于完全二叉树的优秀性质,利用数组存储二叉树即节省空间,又方便索引(若根结点的序号为 1,那么对于树中任意节点 i,其左子节点序号为 2*i,右子节点序号为 2*i+1)。
为了方便存储和索引,(二叉)堆可以用完全二叉树的形式进行存储。存储的方式如下图所示:
堆的操作
堆的更新操作主要包括两种 : 插入元素 和 删除堆顶元素。操作过程需要着重掌握和理解。在进入正题之前,再重申一遍,堆是一个公平的公司,有能力的人自然会走到与他能力所匹配的位置
插入元素
插入元素,作为一个新入职的员工,初来乍到,这个员工需要从基层做起
1.将要插入的元素放到最后
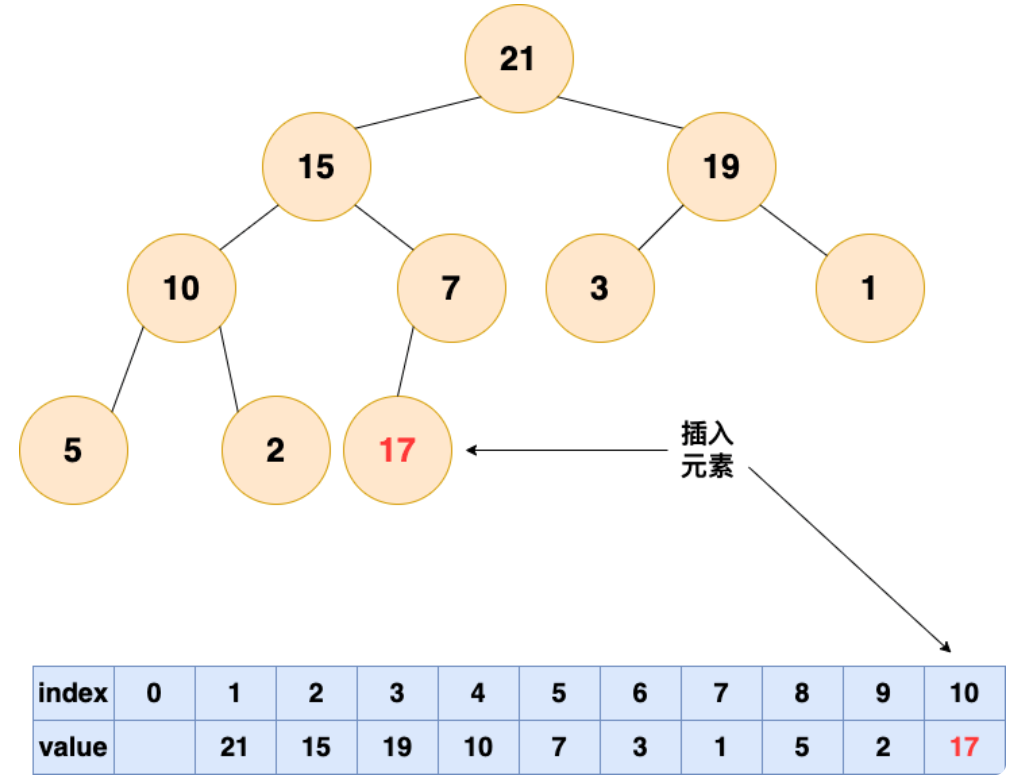
2.从底向上,如果父结点比该元素小,则该节点和父结点交换,直到无法交换
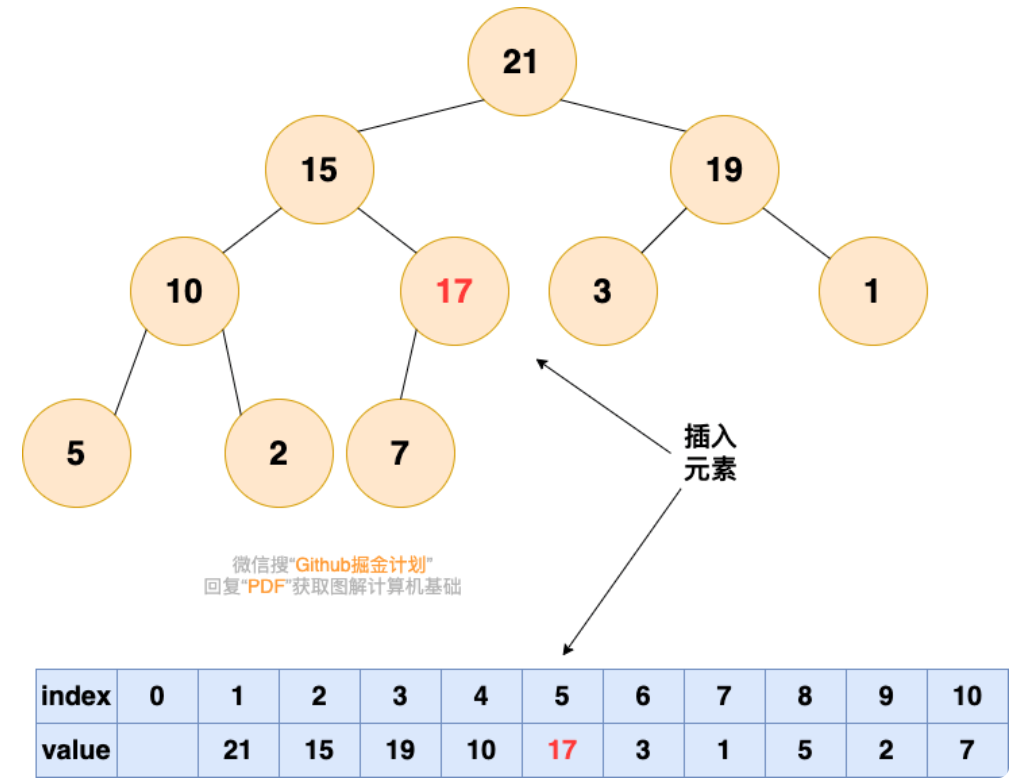
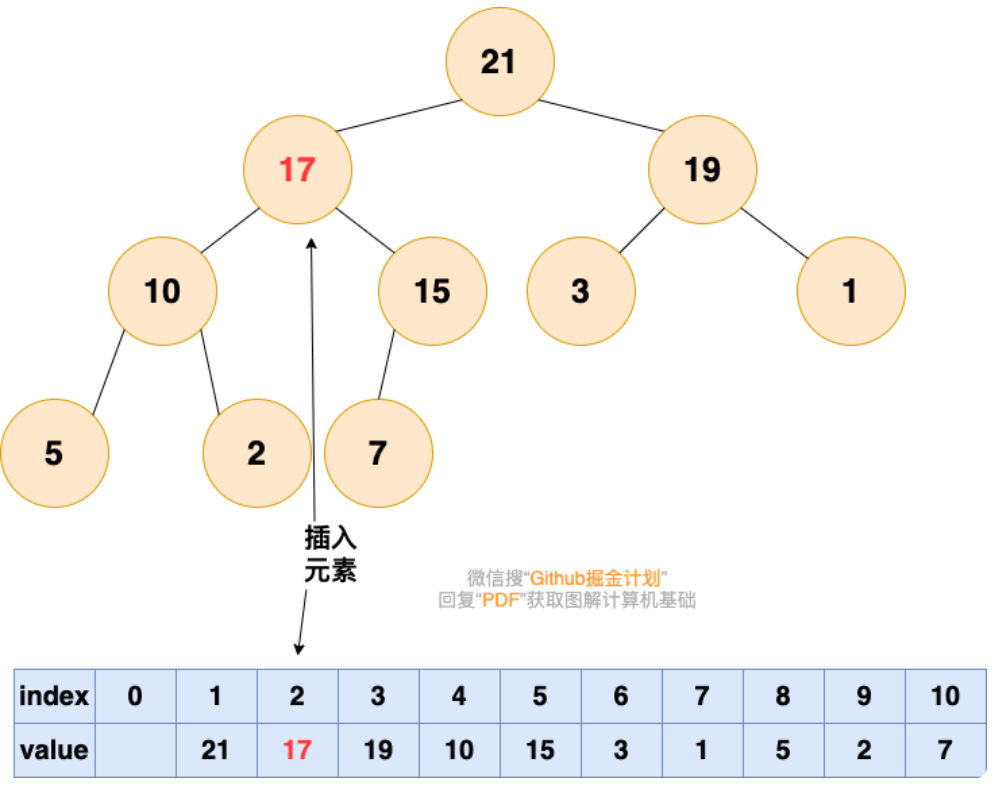
删除堆顶元素
根据堆的性质可知,最大堆的堆顶元素为所有元素中最大的,最小堆的堆顶元素是所有元素中最小的。当我们需要多次查找最大元素或者最小元素的时候,可以利用堆来实现。
删除堆顶元素后,为了保持堆的性质,需要对堆的结构进行调整,我们将这个过程称之为"堆化",堆化的方法分为两种:
- 一种是自底向上的堆化,上述的插入元素所使用的就是自底向上的堆化,元素从最底部向上移动。
- 另一种是自顶向下堆化,元素由最顶部向下移动。在讲解删除堆顶元素的方法时,我将阐述这两种操作的过程,大家可以体会一下二者的不同。
自底向上堆化
首先删除堆顶元素,使得数组中下标为 1 的位置空出。
在堆这个公司中,会出现老大离职的现象,老大离职之后,他的位置就空出来了。那么他的位置由谁来接替呢,当然是他的直接下属了,谁能力强就让谁上呗
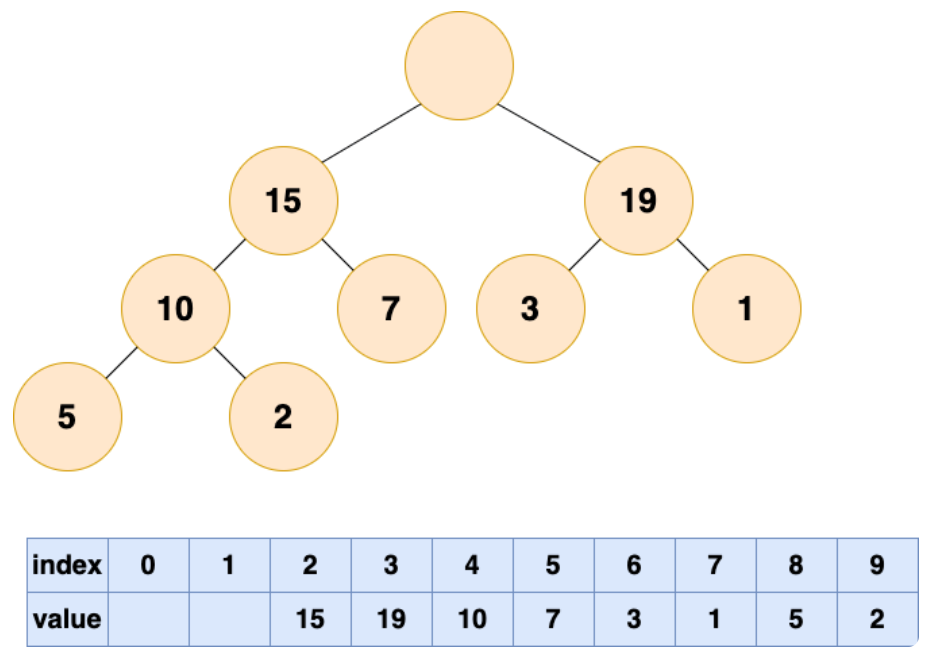
比较根结点的左子节点和右子节点,也就是下标为 2,3 的数组元素,将较大的元素填充到根结点(下标为 1)的位置。
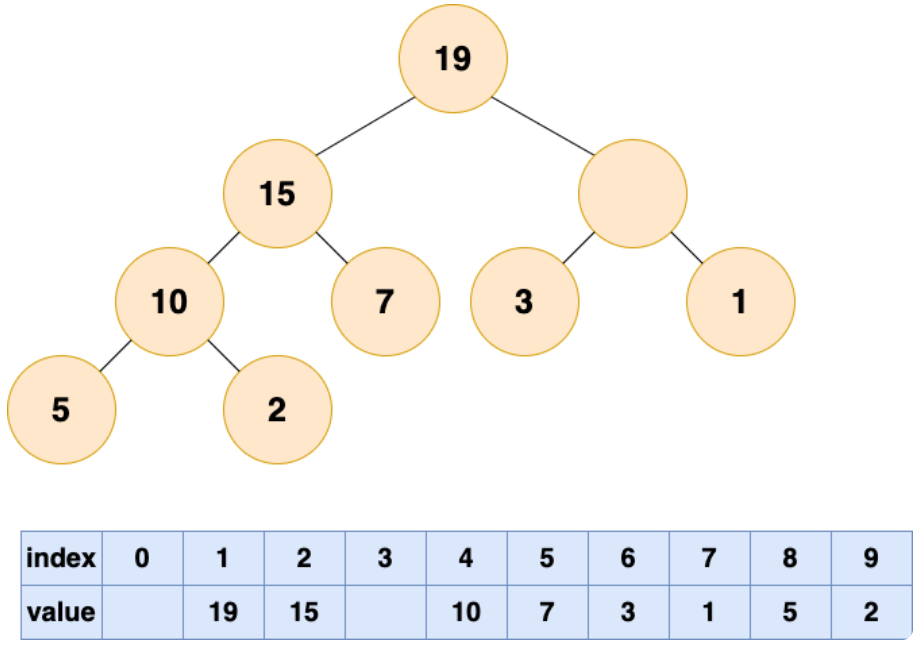
这个时候又空出一个位置了,老规矩,谁有能力谁上
一直循环比较空出位置的左右子节点,并将较大者移至空位,直到堆的最底部
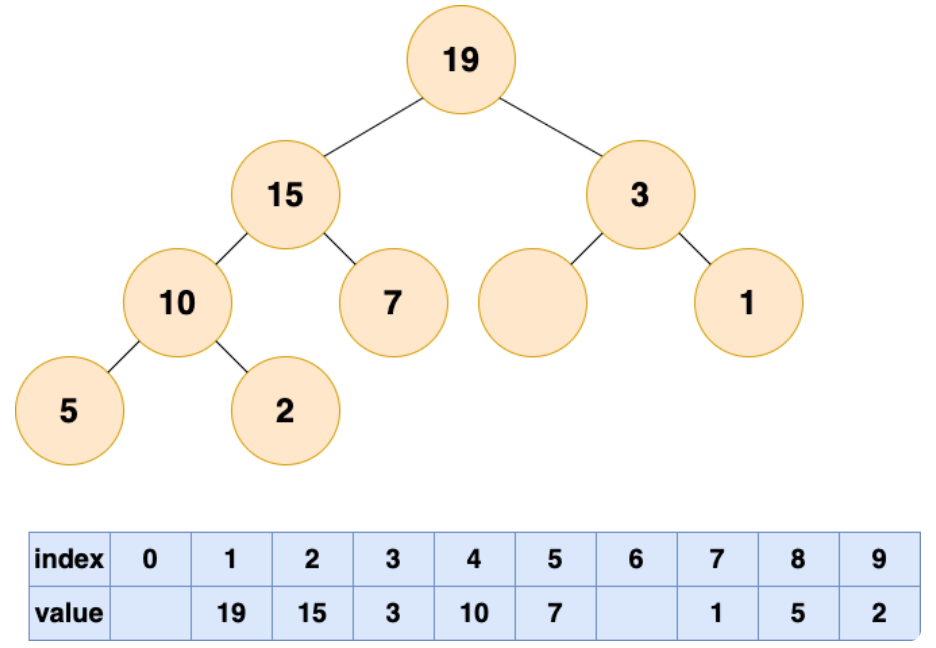
这个时候已经完成了自底向上的堆化,没有元素可以填补空缺了,但是,我们可以看到数组中出现了“气泡”,这会导致存储空间的浪费。接下来我们试试自顶向下堆化。
自顶向下堆化
自顶向下的堆化用一个词形容就是“石沉大海”,那么第一件事情,就是把石头抬起来,从海面扔下去。这个石头就是堆的最后一个元素,我们将最后一个元素移动到堆顶。

然后开始将这个石头沉入海底,不停与左右子节点的值进行比较,和较大的子节点交换位置,直到无法交换位置。
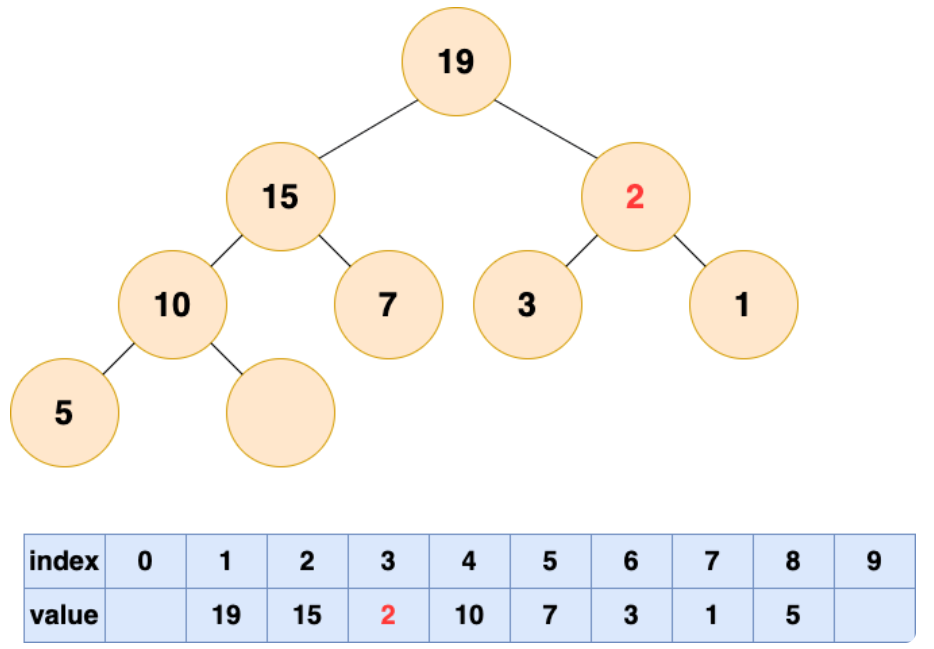
堆的操作总结
- 插入元素:先将元素放至数组末尾,再自底向上堆化,将末尾元素上浮
- 删除堆顶元素:删除堆顶元素,将末尾元素放至堆顶,再自顶向下堆化,将堆顶元素下沉。也可以自底向上堆化,只是会产生“气泡”,浪费存储空间。最好采用自顶向下堆化的方式。
堆排序
堆排序的过程分为两步:
- 第一步是建堆,将一个无序的数组建立为一个堆
- 第二步是排序,将堆顶元素取出,然后对剩下的元素进行堆化,反复迭代,直到所有元素被取出为止。
建堆
如果你已经足够了解堆化的过程,那么建堆的过程掌握起来就比较容易了。建堆的过程就是一个对所有非叶节点的自顶向下堆化过程。
首先要了解哪些是非叶节点,最后一个节点的父结点及它之前的元素,都是非叶节点。也就是说,如果节点个数为 n,那么我们需要对 n/2 到 1 的节点进行自顶向下(沉底)堆化。
具体过程如下图:

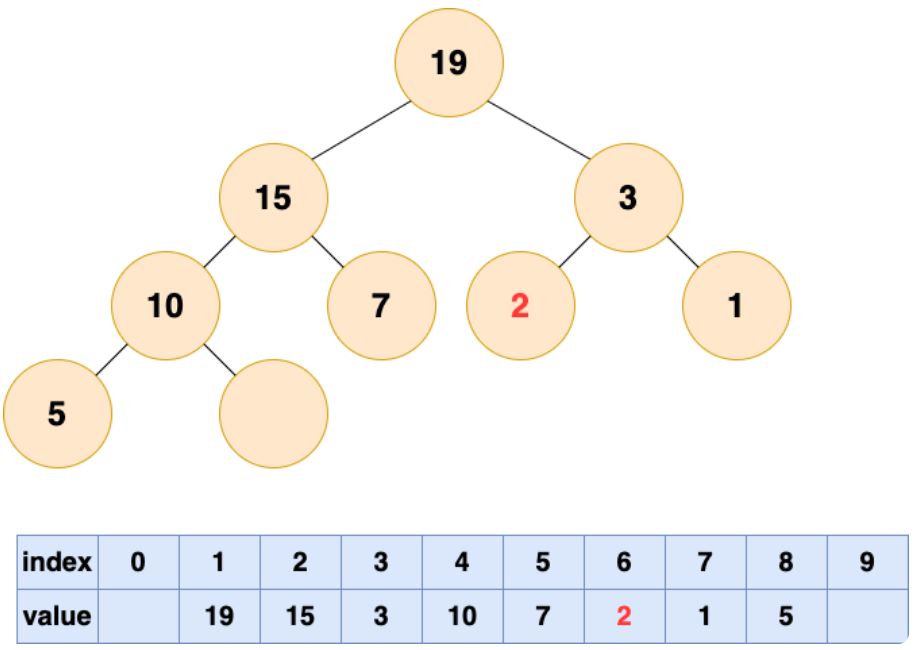
将初始的无序数组抽象为一棵树,图中的节点个数为 6,所以 4,5,6 节点为叶节点,1,2,3 节点为非叶节点,所以要对 1-3 号节点进行自顶向下(沉底)堆化,注意,顺序是从后往前堆化,从 3 号节点开始,一直到 1 号节点。
3 号节点堆化结果:

2 号节点堆化结果:
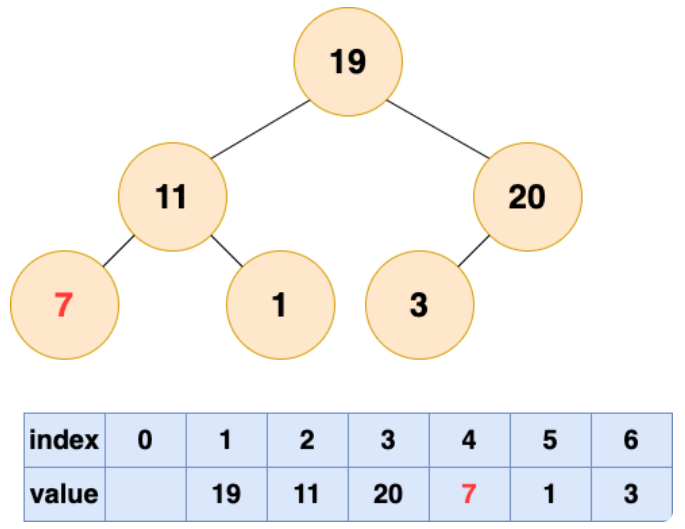
1 号节点堆化结果:
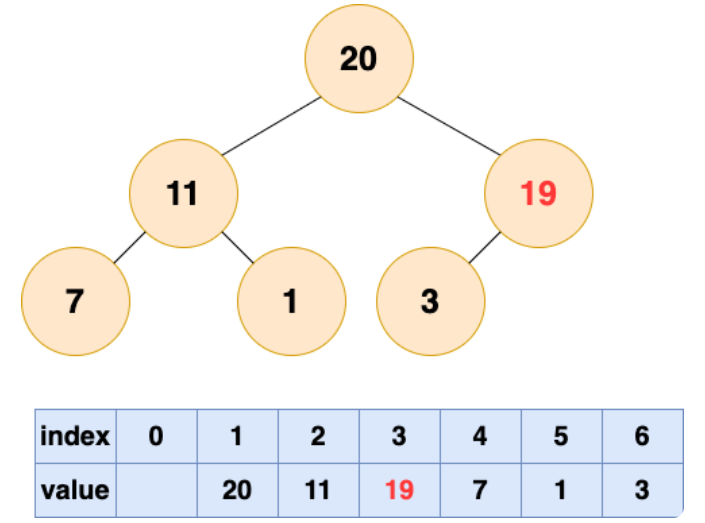
至此,数组所对应的树已经成为了一个最大堆,建堆完成!
排序
由于堆顶元素是所有元素中最大的,所以我们重复取出堆顶元素,将这个最大的堆顶元素放至数组末尾,并对剩下的元素进行堆化即可。
现在思考两个问题:
- 删除堆顶元素后需要执行自顶向下(沉底)堆化还是自底向上(上浮)堆化?
- 取出的堆顶元素存在哪,新建一个数组存?
先回答第一个问题,我们需要执行自顶向下(沉底)堆化,这个堆化一开始要将末尾元素移动至堆顶,这个时候末尾的位置就空出来了,由于堆中元素已经减小,这个位置不会再被使用,所以我们可以将取出的元素放在末尾。
机智的小伙伴已经发现了,这其实是做了一次交换操作,将堆顶和末尾元素调换位置,从而将取出堆顶元素和堆化的第一步(将末尾元素放至根结点位置)进行合并。
详细过程如下图所示:
取出第一个元素并堆化:
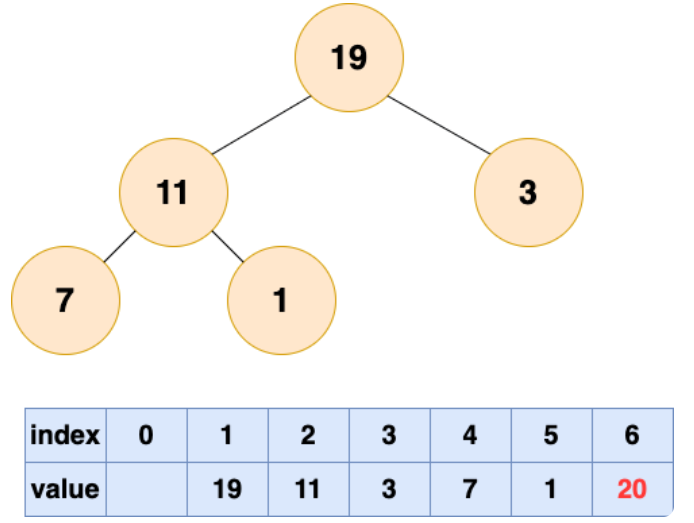
取出第二个元素并堆化:
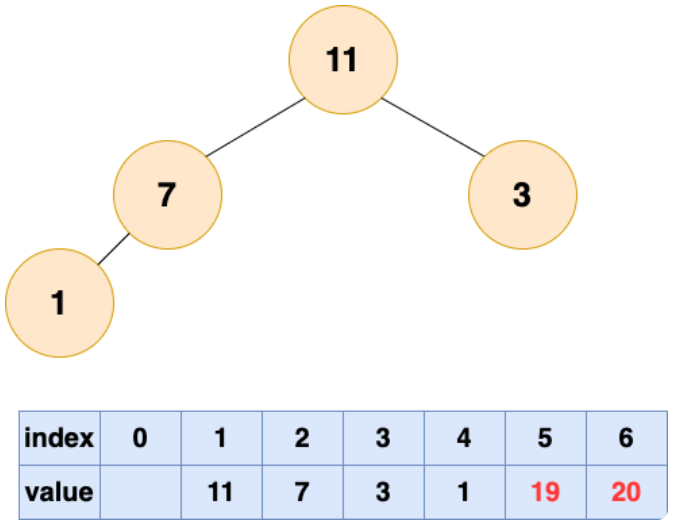
取出第三个元素并堆化:
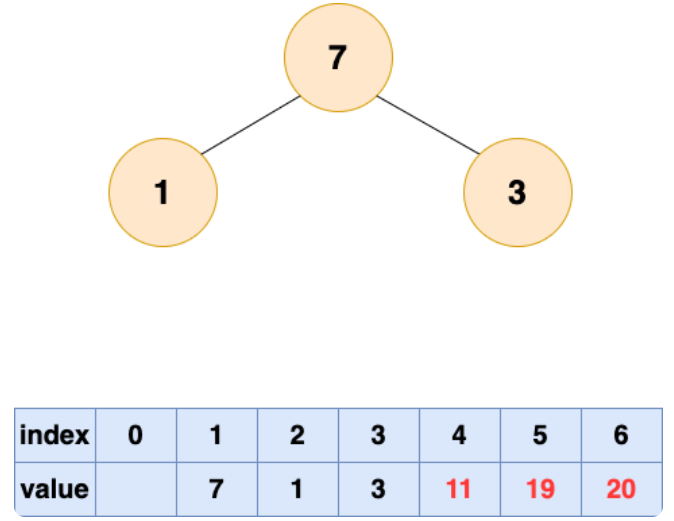
取出第四个元素并堆化:
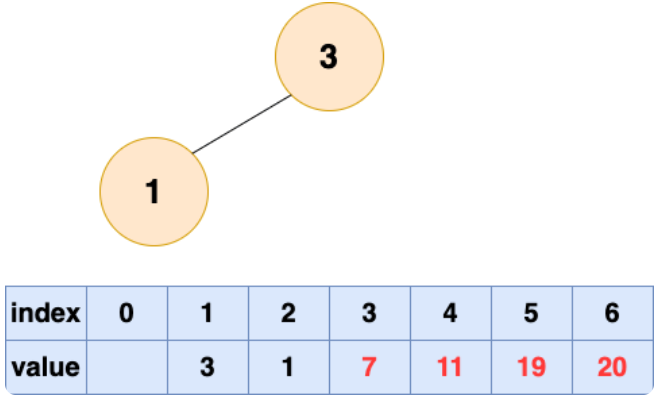
取出第五个元素并堆化:
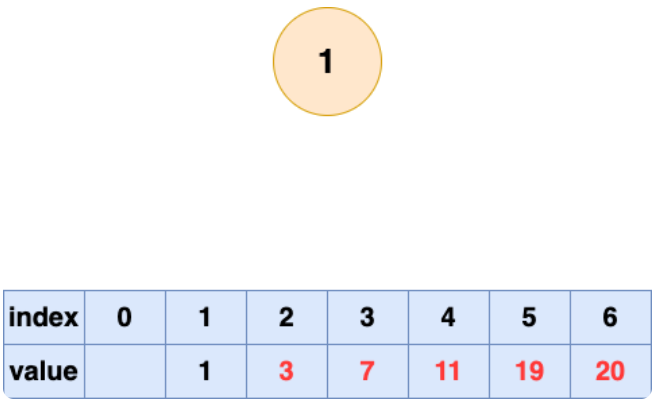
取出第六个元素并堆化:

堆排序完成!
相关文章:

数据结构—堆
什么是堆 堆是一种特殊的树形结构,其中每个节点都有一个值。堆可以分为两种类型:最大堆和最小堆。在最大堆中,每个节点的值都大于等于其子节点的值;而在最小堆中,每个节点的值都小于等于其子节点的值。这种特性使得堆…...

Kubernetes学习笔记8
Kubernetes集群客户端工具kubectl 我们已经能够部署Kubernetes了,那么我们如何使用Kubernetes集群运行企业的应用程序呢?那么,我们就需要使用命令行工具kubectl。 kubectl就是控制Kubernetes的驾驶舱,它允许你执行所有可能的Kube…...
[渗透利器]在线渗透测试工具箱?测评
前言 hxd更新完了在线工具箱,受邀写一下使用体验以及测评 使用体验 这个工具箱设计的比较轻便,以往用过的工具箱大多都是以离线打包的方式发布,该工具箱,作者自己掏钱自己买服务器,自己买带宽,先生大义。…...
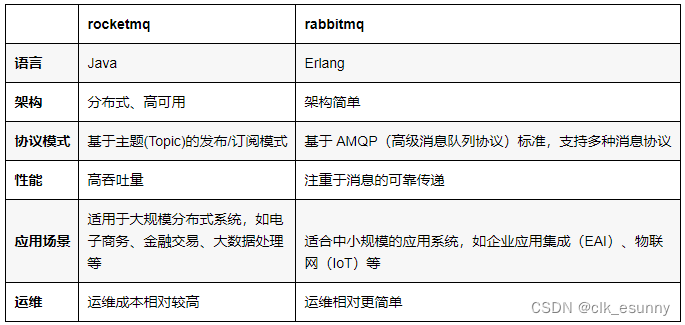
rocketmq和rabbitmq总是分不清?
1. 官方解答 摘自百度搜索: 2. 通俗易懂的回答...

利用Python ARM网关仓储物流AGV小车控制器
在现代智慧物流体系中,高效的信息管理系统是物流中心实现精准跟踪货物、科学管理库存及优化配送路线的关键环节。通过采用ARM架构的工控机或网关,并结合Python的二次开发能力,可以有效集成并强化物流管理系统的数据处理与通信功能,…...
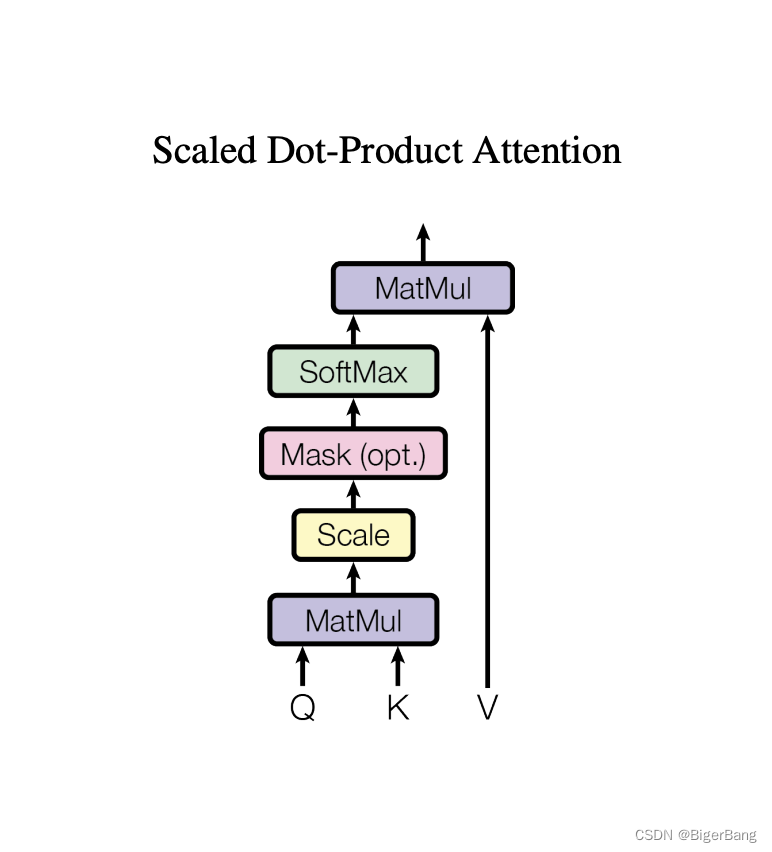
Transformer详解和知识点总结
目录 1. 注意力机制1.1 注意力评分函数1.2 多头注意力(Multi-head self-attention) 2. Layer norm3. 模型结构4. Attention在Transformer中三种形式的应用 论文:https://arxiv.org/abs/1706.03762 李沐B站视频:https://www.bilibi…...

【Ubuntu】update-alternatives 命令详解
1、查看所有候选项 sudo update-alternatives --list java 2、更换候选项 sudo update-alternatives --config java 3、自动选择优先级最高的作为默认项 sudo update-alternatives --auto java 4、删除候选项 sudo update-alternatives --rem…...

数据结构之堆练习题及PriorityQueue深入讲解!
题外话 上午学了一些JavaEE初阶知识,下午继续复习数据结构内容 正题 本篇内容把堆的练习题做一下 第一题 1.下列关键字序列为堆的是:( A ) A: 100,60,70,50,32,65 B: 60,70,65,50,32,100 C: 65,100,70,32,50,60 D: 70,65,100,32,50,60 E: 32,50,100,70,65,60 …...

MySQL——Linux安装包
一、下载安装包 MySQL下载路径: MySQL :: MySQL Downloads //默认下载的企业版MySQL 下载社区版MySQL MySQL :: MySQL Community Downloads 1、源码下载 2、仓库配置 3、二进制安装包 基于官方仓库安装 清华centos 软件仓库: Index of /cen…...

MySQL学习笔记(数据类型, DDL, DML, DQL, DCL)
Learning note 1、前言2、数据类型2.1、数值类型2.2、字符串类型2.3、日期类型 3、DDL总览数据库/表切换数据库查看表内容创建数据库/表删除数据库/表添加字段删除字段表的重命名修改字段名(以及对应的数据类型) 4、DML往字段里写入具体内容修改字段内容…...
)
Asible管理变量与事实——管理变量(1)
Ansible简介 Ansible支持利用变量来储存值,并在Ansible项目的所有文件中重复使用这些值。这可以简化项目的创建和维护,并减少错误的数量。 通过变量,您可以轻松地在Ansible项目中管理给定环境的动态值。例如,变量可能包含下面这些…...

【微服务】------微服务架构技术栈
目前微服务早已火遍大江南北,对于开发来说,我们时刻关注着技术的迭代更新,而项目采用什么技术栈选型落地是开发、产品都需要关注的事情,该篇博客主要分享一些目前普遍公司都在用的技术栈,快来分享一下你当前所在用的技…...
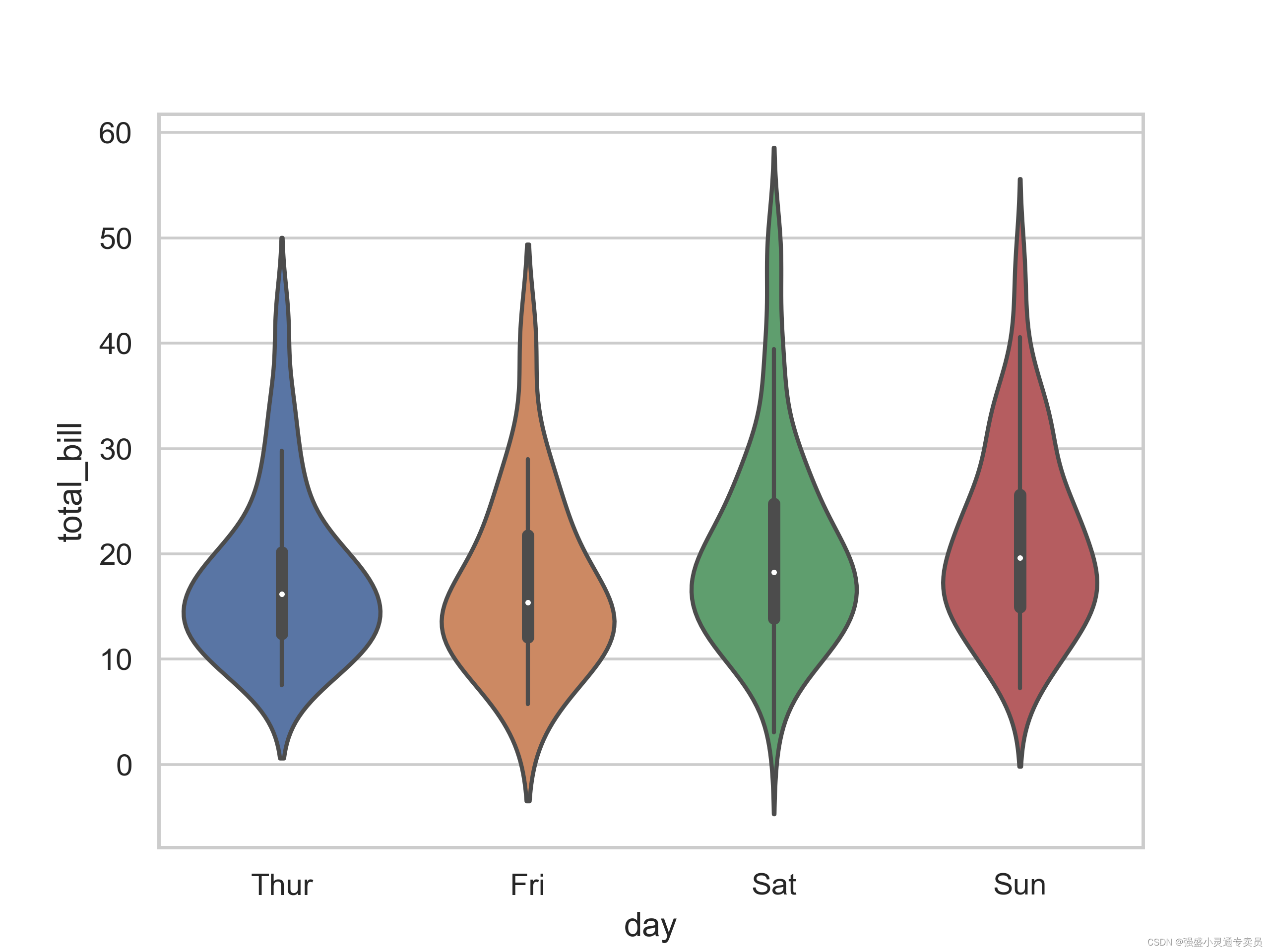
【SCI绘图】【小提琴系列1 python】绘制按分类变量分组的垂直小提琴图
SCI,CCF,EI及核心期刊绘图宝典,爆款持续更新,助力科研! 本期分享: 【SCI绘图】【小提琴系列1 python】绘制按分类变量分组的垂直小提琴图,文末附完整代码 小提琴图是一种常用的数据可视化工具…...
docker------docker入门
🎈个人主页:靓仔很忙i 💻B 站主页:👉B站👈 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:Linux 🤝希望本文对您有所裨益,如有不足之处&#…...

终极数据传输隐秘通道
SOCKS5代理作为网络请求中介的高级形态,提供了一种方法,通过它,数据包在传达其最终目的地前,首先经过一个第三方服务器。这种代理的先进之处在于其对各种协议的支持,包括HTTP、FTP和SMTP,以及它的认证机制&…...

Qt中的事件与事件处理
Qt框架中的事件处理机制是其GUI编程的核心部分,它确保了用户与应用程序之间的交互能够得到正确的响应。以下是对Qt事件处理机制的详细讲解以及提供一些基本示例。 1. 事件与事件处理简介 事件:在Qt中,所有的事件都是从QEvent基类派生出来的&…...
中间件漏洞攻防学习总结
前言 面试常问的一些中间件,学习总结一下。以下环境分别使用vulhub和vulfocus复现。 Apache apache 文件上传 (CVE-2017-15715) 描述: Apache(音译为阿帕奇)是世界使用排名第一的Web服务器软件。它可以运行在几乎所有广泛使用的计算机平台上,由于其跨…...

HarmonyOS开发实例:【分布式数据管理】
介绍 本示例展示了在eTS中分布式数据管理的使用,包括KVManager对象实例的创建和KVStore数据流转的使用。 通过设备管理接口[ohos.distributedDeviceManager],实现设备之间的kvStore对象的数据传输交互,该对象拥有以下能力 ; 1、注册和解除注…...

蓝桥杯——运动会
题目 n 个运动员参加一个由 m 项运动组成的运动会,要求每个运动员参加每个项目。每个运动员在每个项目都有一个成绩,成绩越大排名越靠前。每个项目,不同运功员的成绩不会相 同,因此排名不会相同。(但是不同项目可能成绩会相同) 每…...

如何搭建APP分发平台分发平台搭建教程
搭建一个APP分发平台可以帮助开发者更好地分发和管理他们的应用程序。下面是一个简要的教程,介绍如何搭建一个APP分发平台。 1.确定需求和功能:首先,确定你的APP分发平台的需求和功能。考虑以下几个方面: 用户注册和登录ÿ…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
