2024.3.15力扣每日一题——卖木头块
2024.3.15
- 题目来源
- 我的题解
- 方法一 记忆化搜索(自顶向下)
- 方法二 动态规划(自底向上)
题目来源
力扣每日一题;题序:2312
我的题解
方法一 记忆化搜索(自顶向下)
用 f(x,y)表示当木块的高和宽分别是 x 和 y 时,可以得到的最多钱数。我们需要考虑三种情况:
- 如果数组 prices 中存在 (x,y,price) 这一三元组,那么可以将木块以 prices 的价格卖出。为了快速判断存在性,可以使用一个哈希映射来进行存储,即哈希映射的键为 ( h i h_i hi, w i w_i wi),值为 p r i c e i price_i pricei ,这样就可以根据木块的高和宽,在 O(1) 的时间得到对应的价格。这种情况的状态转移方程为:
f(x,y)=price。- 如果 x>1,那么可以沿水平方向将木块切成两部分,它们的高分别是 i ( 1 ≤ i < x ) i~(1 \leq i < x) i (1≤i<x)和 x−i,宽均为 y。因此可以得到状态转移方程:
f ( x , y ) = max 1 ≤ i < x { f ( i , y ) + f ( x − i , y ) } f(x, y) = \max_{1 \leq i < x} \big\{ f(i, y) + f(x-i, y) \big\} f(x,y)=max1≤i<x{f(i,y)+f(x−i,y)}- 如果 y>1,那么可以沿垂直方向将木块切成两部分,它们的宽分别是 j ( 1 ≤ j < y ) j~(1 \leq j < y) j (1≤j<y) 和 y−j,高均为 x。因此可以得到状态转移方程:
f ( x , y ) = max 1 ≤ j < y { f ( x , j ) + f ( x , y − j ) } f(x, y) = \max_{1 \leq j < y} \big\{ f(x, j) + f(x, y-j) \big\} f(x,y)=max1≤j<y{f(x,j)+f(x,y−j)}当有多种情况满足时,我们需要选择它们中的较大值。最终的答案即为 f(m,n)。
时间复杂度:O(mn(m+n)+p),其中 p 是数组 prices的长度。
空间复杂度:O(mn+p),即为哈希映射和动态规划的数组需要使用的空间。
public long sellingWood(int m, int n, int[][] prices) {Map<String, Integer> value = new HashMap<>();for (int[] price : prices) {value.put(price[0]+"-"+price[1], price[2]);}//记忆化搜索的备忘录long[][] memo = new long[m + 1][n + 1];for (long[] row : memo) {Arrays.fill(row, -1);}return dfs(m, n, value, memo);
}public long dfs(int x, int y, Map<String, Integer> value, long[][] memo) {if (memo[x][y] != -1) {return memo[x][y];}String key = x+"-"+y;long ret = value.containsKey(key) ? value.get(key) : 0;if (x > 1) {//沿水平方向切for (int i = 1; i < x; i++) {ret = Math.max(ret, dfs(i, y, value, memo) + dfs(x - i, y, value, memo));}}if (y > 1) {//沿垂直方向切for (int j = 1; j < y; j++) {ret = Math.max(ret, dfs(x, j, value, memo) + dfs(x, y - j, value, memo));}}memo[x][y] = ret;return ret;
}
方法二 动态规划(自底向上)
时间复杂度:O( m 2 + n 2 + p m^2+n^2+p m2+n2+p)
空间复杂度:O(mn+p)
public long sellingWood(int m, int n, int[][] prices) {Map<String, Integer> value = new HashMap<>();for (int[] price : prices) {value.put(price[0] + "-" + price[1], price[2]);}long[][] dp = new long[m + 1][n + 1];for (int x = 1; x <= m; x++) {for (int y = 1; y <= n; y++) {String key = x + "-" + y;long ret = value.containsKey(key) ? value.get(key) : 0;if (x > 1) {// 沿水平方向切for (int i = 1; i < x; i++) {ret = Math.max(ret, dp[i][y] + dp[x - i][y]);}}if (y > 1) {// 沿垂直方向切for (int j = 1; j < y; j++) {ret = Math.max(ret, dp[x][j] + dp[x][y - j]);}}dp[x][y] = ret;}}return dp[m][n];
}
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.3.15力扣每日一题——卖木头块
2024.3.15 题目来源我的题解方法一 记忆化搜索(自顶向下)方法二 动态规划(自底向上) 题目来源 力扣每日一题;题序:2312 我的题解 方法一 记忆化搜索(自顶向下) 用 f(x,y)表示当木…...
vue快速入门(七)内联语句
注释很详细,直接上代码 上一篇 新增内容 button点击事件绑定内联语句写法与要求 源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-wid…...
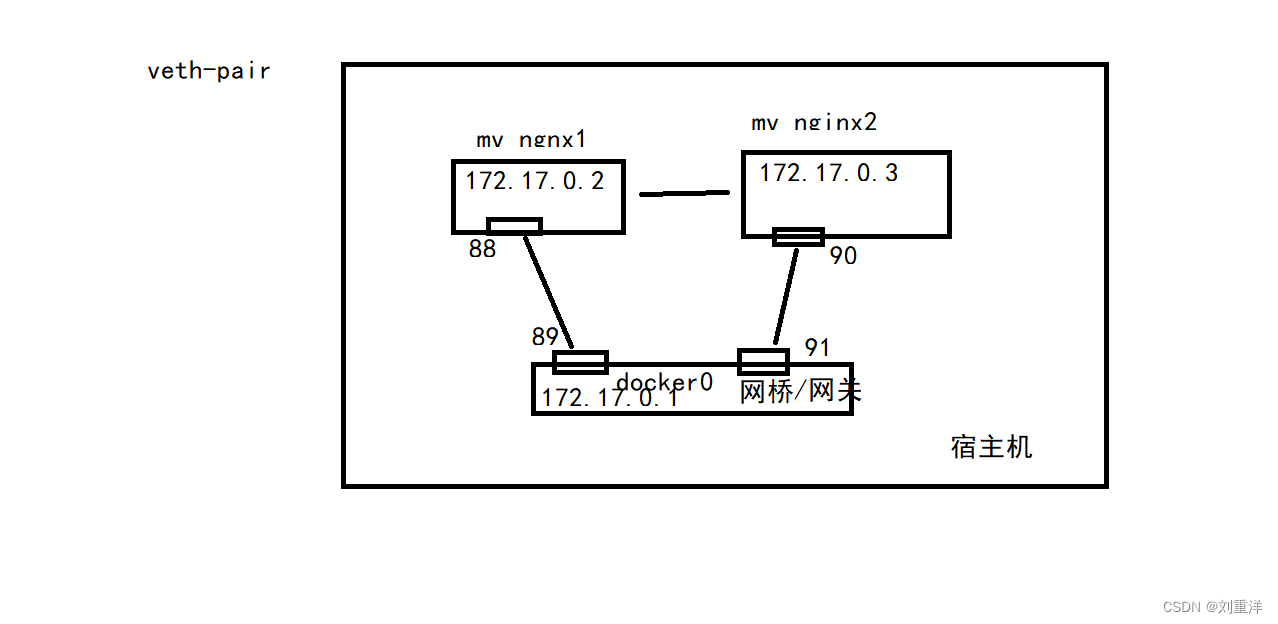
Docker实战教程 第2章 Docker基础
3-1 Docker介绍 什么是Docker 虚拟化,容器 Docker 是一个开源的应用容器引擎,基于 Go 语言 并遵从Apache2.0协议开源。 Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的 Linux 机器上&…...
)
【S32K3 MCAL配置】-3.2-CANFD配置-发送“经典CAN/CANFD标准帧“和“经典CAN/CANFD扩展帧“(基于MCAL+FreeRTOS)
"><--返回「Autosar_MCAL高阶配置」专栏主页--> 目录 实现的架构:基于MCAL层 前期准备工作: 1 评估板S32K312EVB-Q172中CAN外设...

【airtest】自动化入门教程(四)Poco元素定位
目录 一、基础操作 1、通过属性名等方式 2、通过属性组合 3、子节点方式 4、子节点加属性组合方式 5、孙节点offspring 6、兄弟节点sibling 7、父节点parent 8、正则表达式 9、直到某个元素出现 10、直到某个元素消失 二、通过局部坐标定位 1、使用局部坐标系的cli…...

Go语言中如何处理goroutine和循环变量
对goroutine和循环变量处理不当可能是Go开发人员在编写并发应用程序时最常犯的错误之一。让我们看一个具体的例子,然后我们将定义发生此类错误的条件以及如何防止发生这类错误。 在下面的示例中,我们初始化一个切片,然后在作为新goroutine执行的闭包中访问这个元素: s := …...

Pytest教程:一文了解如何使用 pytest_runtest_makereport 修改 Pytest 测试报告内容
在软件测试过程中,生成清晰、易读的测试报告对于团队交流、问题追踪和项目进度评估至关重要。Pytest 是一个功能强大的 Python 测试框架,它不仅支持丰富的断言和测试用例组织方式,还提供了灵活的插件系统和钩子函数,可以帮助我们定…...
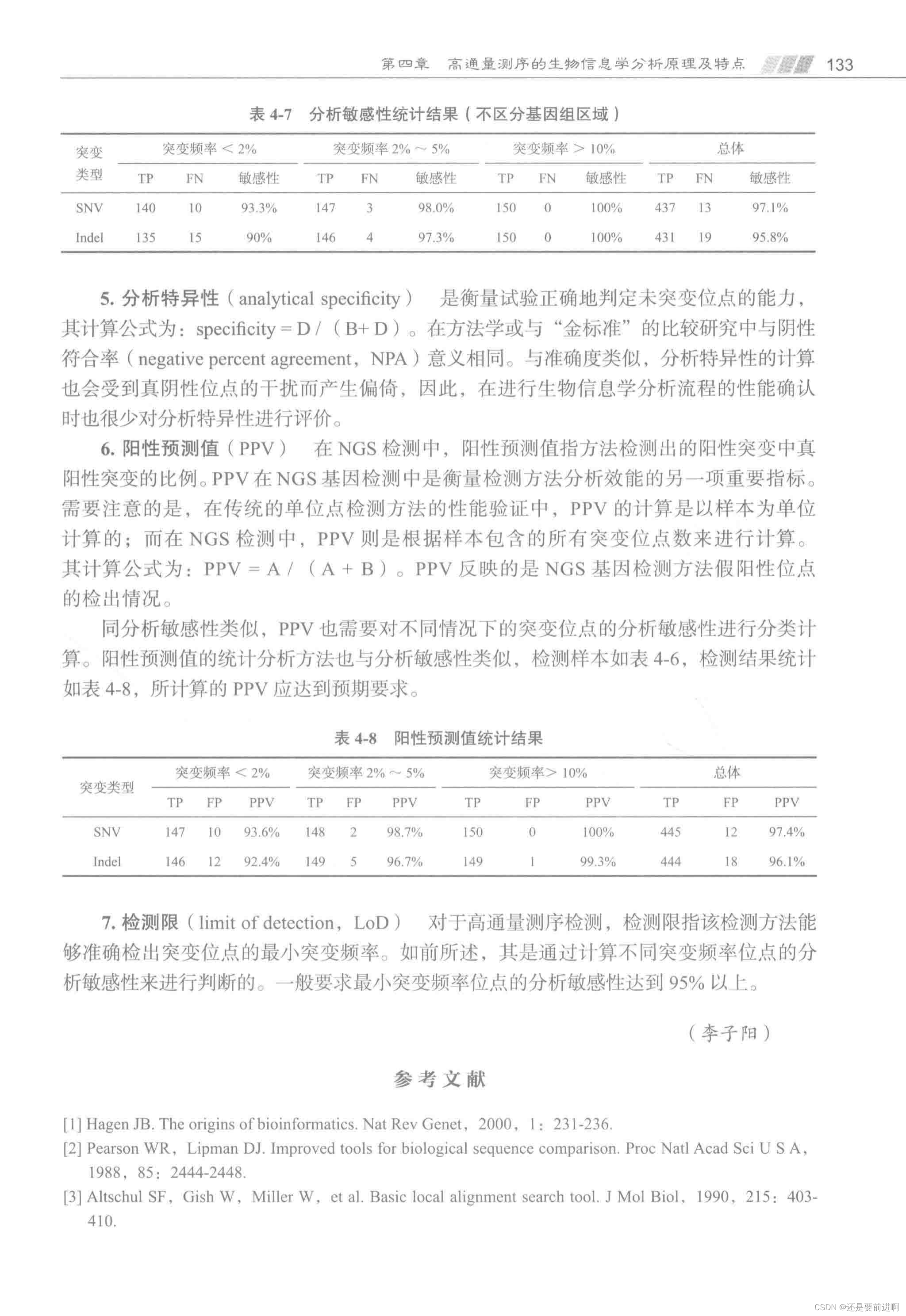
《高通量测序技术》分享,生物信息学生信流程的性能验证,以肿瘤NGS基因检测为例。
这是这本书,第四章第五节的内容,这一部分是以NGS检测肿瘤基因突变为例,描述了其原理和大概流程,这和以前我分享的病原宏基因组高通量测序性能确认方案可以互相补充,大家可以都看一下,但是想要真正的弄懂&am…...

Django+Celery框架自动化定时任务开发
本章介绍使用DjCelery即DjangoCelery框架开发定时任务功能,在Autotestplat平台上实现单一接口自动化测试脚本、业务场景接口自动化测试脚本、App自动化测试脚本、Web自动化测试脚本等任务的定时执行、调度、管理等,从而取代Jenkins上的定时执行脚本和发送…...
解决element-plus table组件 fixed=“right“(left)浮动后横向滚动文字穿透的问题
BUG 版本:element-plus 2.6.1 浏览器:360极速浏览器22.1 (Chromium内核) 组件:el-table组件 问题:在头部/尾部浮动加上斑马条纹后,横向滚动存在文字穿透的问题。具体如图: 白色背景行的文字,…...
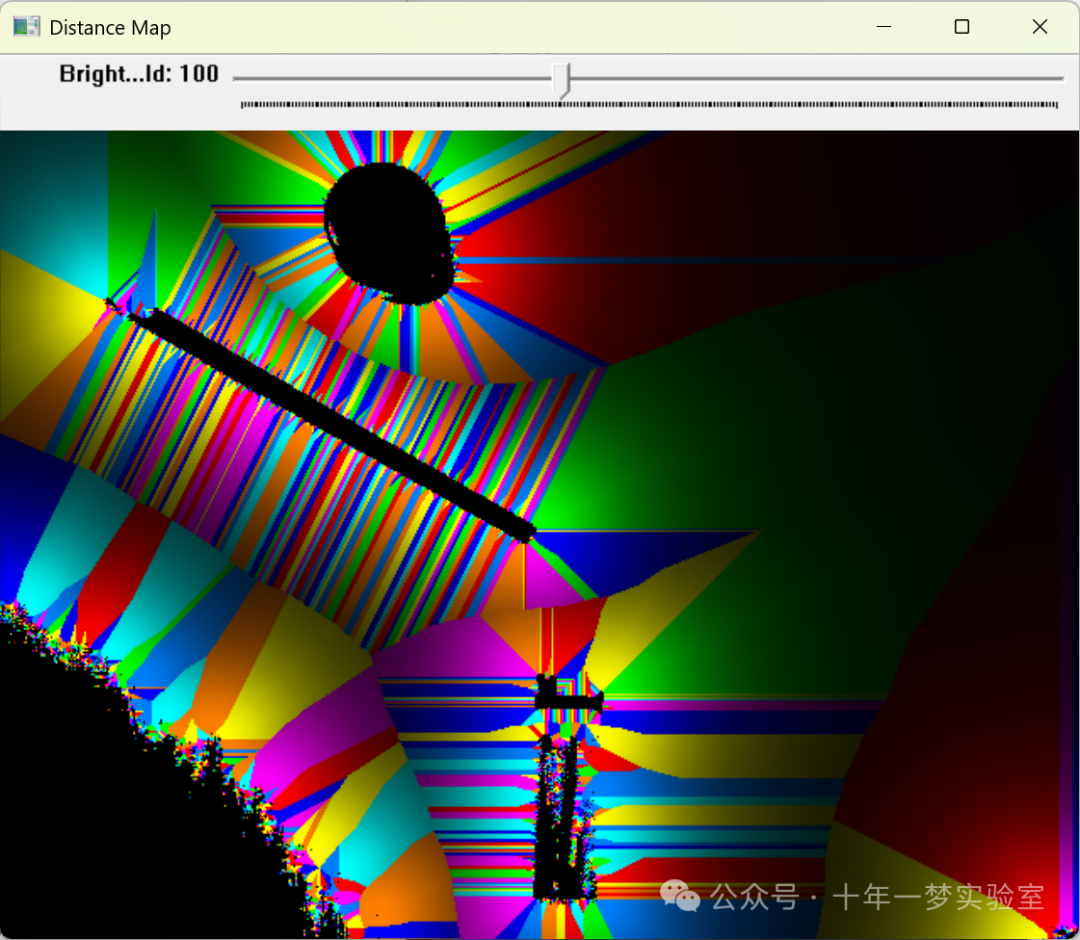
【opencv】示例-distrans.cpp 距离变换
stuff.jpg #include <opencv2/core/utility.hpp> // 包含OpenCV中的核心功能支持库 #include "opencv2/imgproc.hpp" // 包含OpenCV中的图像处理库 #include "opencv2/imgcodecs.hpp" // 包含OpenCV中的图像编解码库 #include "open…...

LVGL V8 代码细读——极致的链表使用
极致的链表的使用 序章碎碎念从redis源码里掏出来的adlist极致的精简的list.hlvgl对链表的巧思lv_ll尾记 序章碎碎念 对于链表,大家应该都不陌生。学过数据结构的,都知道它作为链式储存的基础,重要性不言而喻。 由于本人自动化专业ÿ…...
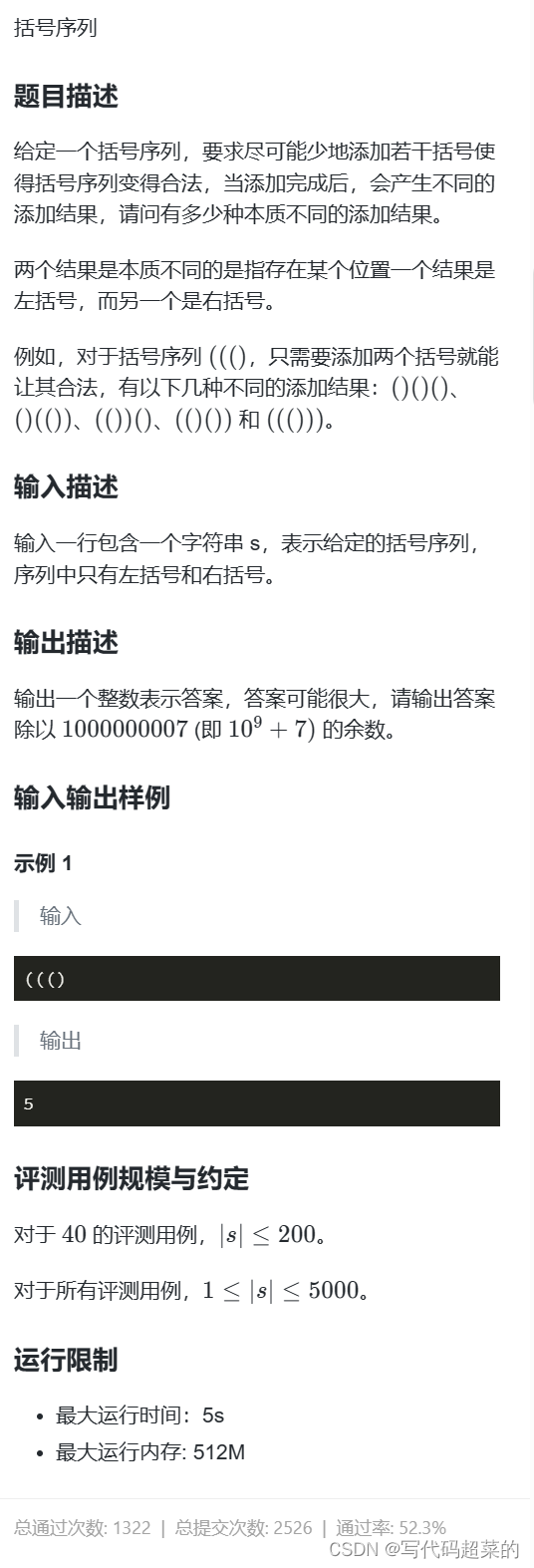
蓝桥杯第十二届c++大学B组详解
目录 1.空间 2.直线 3.路径 4.卡片 5.货物摆放 6.时间显示 7.砝码称重 8.杨辉三角 9.双向排序 10.括号序列 1.空间 题目解析:1Byte 8bit 1kb 1024B 1MB 1024kb; 先将256MB变成Byte 256 * 1024 * 1024; 再将32位 变成Byte就是 32 / 8 4;…...

Tubi 十岁啦!
Tubi 今年十岁了,这十年不可思议,充满奇迹! 从硅谷一个名不见经传的创业小作坊,转变成为四分之一美国电视家庭提供免费流媒体服务的北美领先的平台; 从费尽心力终于签下第一笔内容合作协议,到现在与 450 …...

Qt C++ 实现文件监视源码
以下是使用Qt C++实现文件监视的一个简单示例代码: #include <QCoreApplication> #include <QFileSystemWatcher> #include <QDebug>int main(int argc, char *argv[...
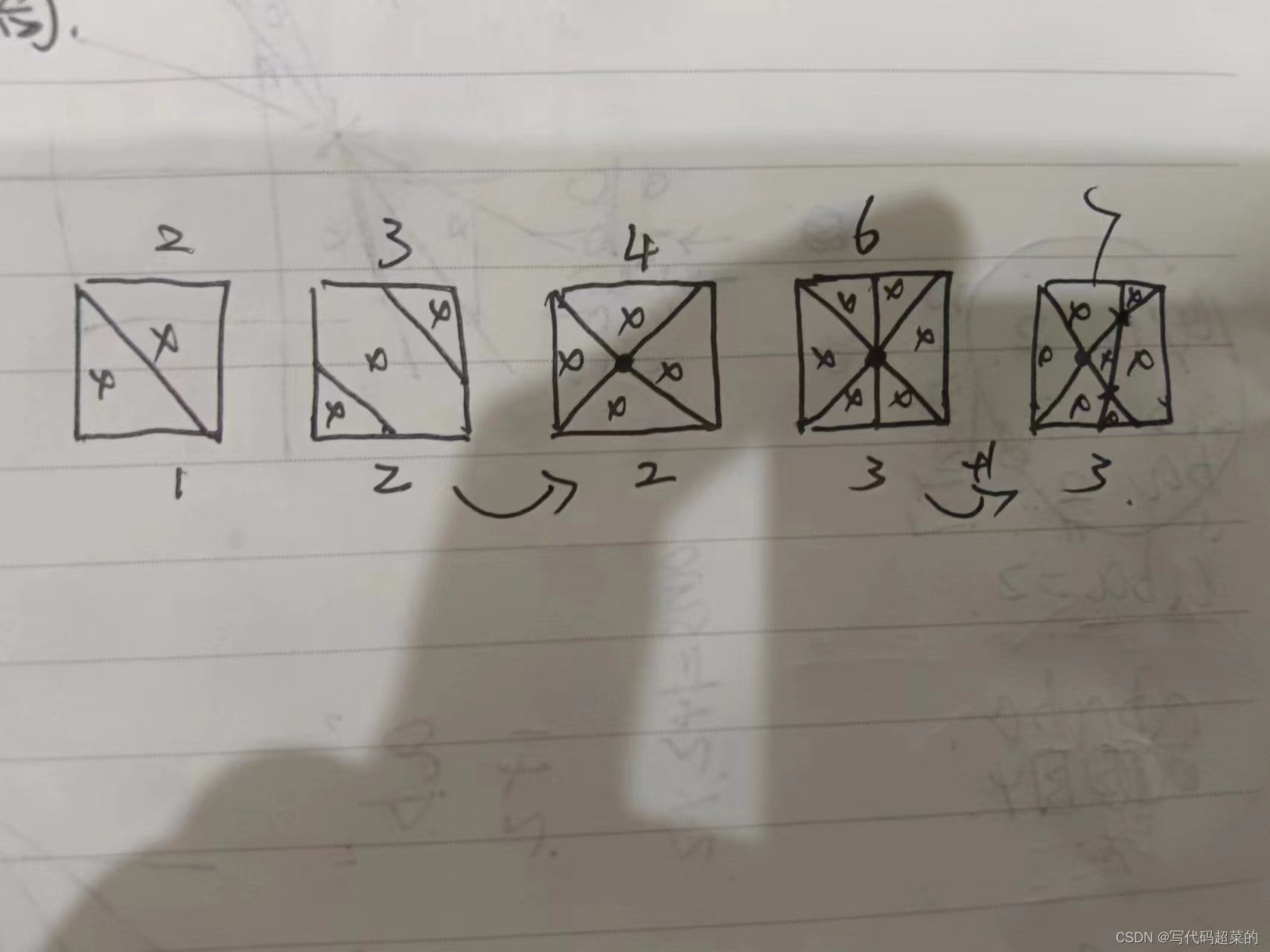
蓝桥杯第十一届c++大学B组详解
目录 1.字符串排序 2.门牌制作 3.即约分数 4.蛇型填数 5.跑步锻炼 6.七段码 7.成绩统计 8.回文日期 9.字串分值和 10.平面切分 1.字符串排序 题目解析:这个题目真没搞懂。有会的大佬教我一下谢谢。 2.门牌制作 题目解析:出过超级多这类题目&am…...

大模型日报2024-04-10
大模型日报 2024-04-10 大模型资讯 微软研究者提出通过可视化思维提升大型语言模型的空间推理能力 摘要: 微软研究者近日提出了一种新方法,旨在通过可视化思维来增强大型语言模型(LLMs)的空间推理能力。尽管LLMs在语言理解和推理任务方面表现…...

redis修改协议改了,有哪些替代品?
Redis 是一款广泛使用的开源内存数据结构存储,它支持多种数据结构,如字符串、哈希表、列表、集合、有序集合等。然而,由于 Redis 最近更改了其开源许可证,一些用户和开发者可能正在寻找替代品。以下是一些 Redis 的替代品…...

《QT实用小工具·十六》IP地址输入框控件
1、概述 源码放在文章末尾 该项目为IP地址输入框控件,主要包含如下功能: 可设置IP地址,自动填入框。 可清空IP地址。 支持按下小圆点自动切换。 支持退格键自动切换。 支持IP地址过滤。 可设置背景色、边框颜色、边框圆角角度。 下面…...
windows 系统下 mysql 数据库的下载与安装(包括升级安装)
windows 系统下 mysql 数据库的下载与安装(包括升级安装) 一、mysql 介绍: MySQL 是一个关系型数据库管理系统,由瑞典 MySQL AB 公司开发,属于 Oracle 旗下产品。 MySQL 是最流行的关系型数据库管理系统之一…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
