【算法刷题 | 二叉树 06】4.10( 路径总和、路径总和 || )

文章目录
- 13.路径总和
- 13.1问题
- 13.2解法一:递归
- 13.2.1递归思路
- (1)确定递归函数参数以及返回值
- (2)确定终止条件
- (3)确定递归逻辑
- 13.2.2代码实现
- 14.路径总和 ||
- 14.1问题
- 14.2解法一:递归
- 14.2.1递归思路
- (1)确定递归函数参数以及返回值
- (2)确定终止条件
- (3)确定递归逻辑
- 14.2.2代码实现
13.路径总和
13.1问题
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
- 示例一:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
13.2解法一:递归
13.2.1递归思路
(1)确定递归函数参数以及返回值
- 参数:节点、计数器(记录从根节点到该节点的值)、targetSum
- 返回值:需要搜索整棵二叉树并且需要处理递归返回值的递归函数就需要返回值,此题使用boolean代表这颗树是否存在路径总和为targetSum的路径
private boolean traversal(TreeNode node,int count,int targetSum)
(2)确定终止条件
- 当当前节点为叶子节点并且count=targetSum时,返回true(该count已经包含当前节点的值了);
- 当当前节点为叶子节点,直接返回false
if(node.left==null && node.right==null && count==targetSum){return true;
}
if(node.left==null && node.right==null){return false;
}
(3)确定递归逻辑
- 因为终止条件是判断叶子节点,所以递归的过程中就不要让空节点进入递归了;
- 若该节点的左右孩子非空,则递归(注意递归函数的count加上左右孩子的值);
- 递归完若发现为true,则直接返回true,否则进行回溯,不要该左孩子节点(count减去该值),进行右孩子节点的查找(回溯);
if(node.left!=null){if(traversal(node.left,count+=node.left.val,targetSum)){return true;}//回溯count-=node.left.val;
}
if(node.right!=null){if(traversal(node.right,count+=node.right.val,targetSum)){return true;1}//回溯count-=node.right.val;
}
return false;
13.2.2代码实现
public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null){return false;}return traversal(root,root.val,targetSum);}private boolean traversal(TreeNode node,int count,int targetSum){if(node.left==null && node.right==null && count==targetSum){return true;}if(node.left==null && node.right==null){return false;}if(node.left!=null){if(traversal(node.left,count+=node.left.val,targetSum)){return true;}//回溯count-=node.left.val;}if(node.right!=null){if(traversal(node.right,count+=node.right.val,targetSum)){return true;}//回溯count-=node.right.val;}return false;}
}
14.路径总和 ||
14.1问题
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和 的路径。
叶子节点 是指没有子节点的节点。
- 示例一:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
14.2解法一:递归
14.2.1递归思路
(1)确定递归函数参数以及返回值
- 参数说明:
- 求根节点到 node 节点的路径之和 == targetSum
- paths存放当前路径
- res存放符合路径总和为targetSum的路径
- count代表从根节点到该节点的路径中和
- 无返回值
private void traversal(TreeNode node, List<Integer> paths, List<List<Integer>> res, int count, int targetSum)
(2)确定终止条件
- 若该节点为叶子节点,则判断count==targetSum,符合则添加该paths到res中,否则返回
if(node.left==null && node.right==null){if(count==targetSum) {res.add(new ArrayList<>(path));}return;
}
(3)确定递归逻辑
if(node.left!=null){paths.add(node.left.val);traversal(node.left,paths,res,count+=node.left.val,targetSum);//回溯paths.remove(paths.size()-1);count-=node.left.val;
}if(node.right!=null){paths.add(node.right.val);traversal(node.right,paths,res,count+=node.right.val,targetSum);//回溯paths.remove(paths.size()-1);count-=node.right.val;
}
14.2.2代码实现
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {int count=0;List<List<Integer>> res=new ArrayList<>();List<Integer> paths=new ArrayList<>();if(root==null){return res;}paths.add(root.val);traversal(root,paths,res,count+=root.val,targetSum);return res;}private void traversal(TreeNode node, List<Integer> paths, List<List<Integer>> res, int count, int targetSum){if(node.left==null && node.right==null){if(count==targetSum){res.add(new ArrayList<>(paths));}return;}if(node.left!=null){paths.add(node.left.val);traversal(node.left,paths,res,count+=node.left.val,targetSum);//回溯paths.remove(paths.size()-1);count-=node.left.val;}if(node.right!=null){paths.add(node.right.val);traversal(node.right,paths,res,count+=node.right.val,targetSum);//回溯paths.remove(paths.size()-1);count-=node.right.val;}}
}

相关文章:

【算法刷题 | 二叉树 06】4.10( 路径总和、路径总和 || )
文章目录 13.路径总和13.1问题13.2解法一:递归13.2.1递归思路(1)确定递归函数参数以及返回值(2)确定终止条件(3)确定递归逻辑 13.2.2代码实现 14.路径总和 ||14.1问题14.2解法一:递归…...
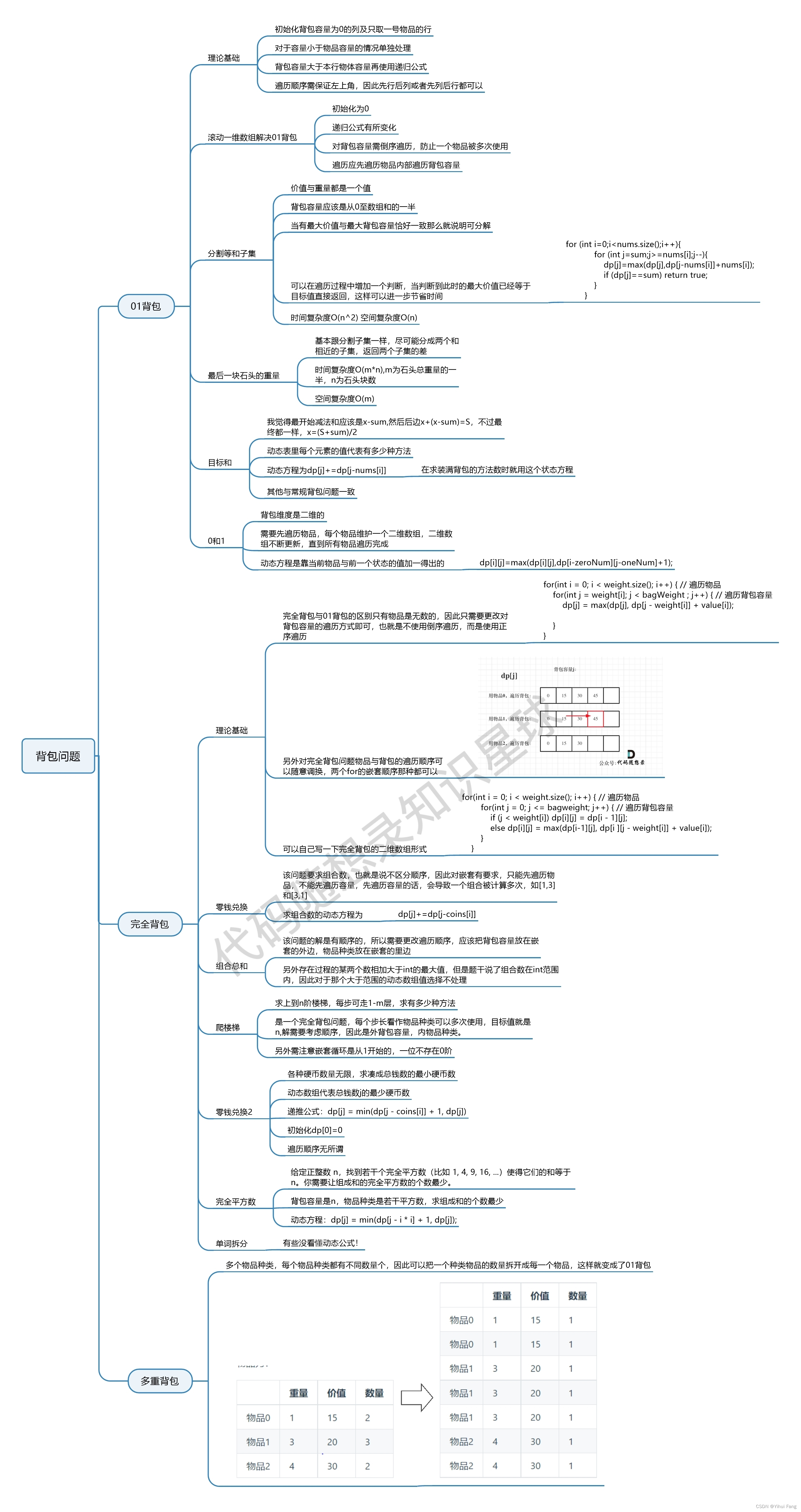
代码学习记录37----动态规划
随想录日记part37 t i m e : time: time: 2024.04.06 主要内容:今天开始要学习动态规划的相关知识了,今天的内容主要涉及四个方面: 完全背包;零钱兑换 II ;组合总和 Ⅳ 和单词拆分 …...

Spring Boot:Web开发之三大组件的整合
Spring Boot 前言Spring Boot 整合 ServletSpring Boot 整合 FilterSpring Boot 整合 Listener前言 在 Web 开发中,Servlet 、Filter 和 Listener 是 Java Web 应用中的三大组件。Servlet 是 Java 代码,通过 Java 的 API 动态的向客户端输出内容。Filter 是处于客户端与服务…...

2024.3.15力扣每日一题——卖木头块
2024.3.15 题目来源我的题解方法一 记忆化搜索(自顶向下)方法二 动态规划(自底向上) 题目来源 力扣每日一题;题序:2312 我的题解 方法一 记忆化搜索(自顶向下) 用 f(x,y)表示当木…...
vue快速入门(七)内联语句
注释很详细,直接上代码 上一篇 新增内容 button点击事件绑定内联语句写法与要求 源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-wid…...
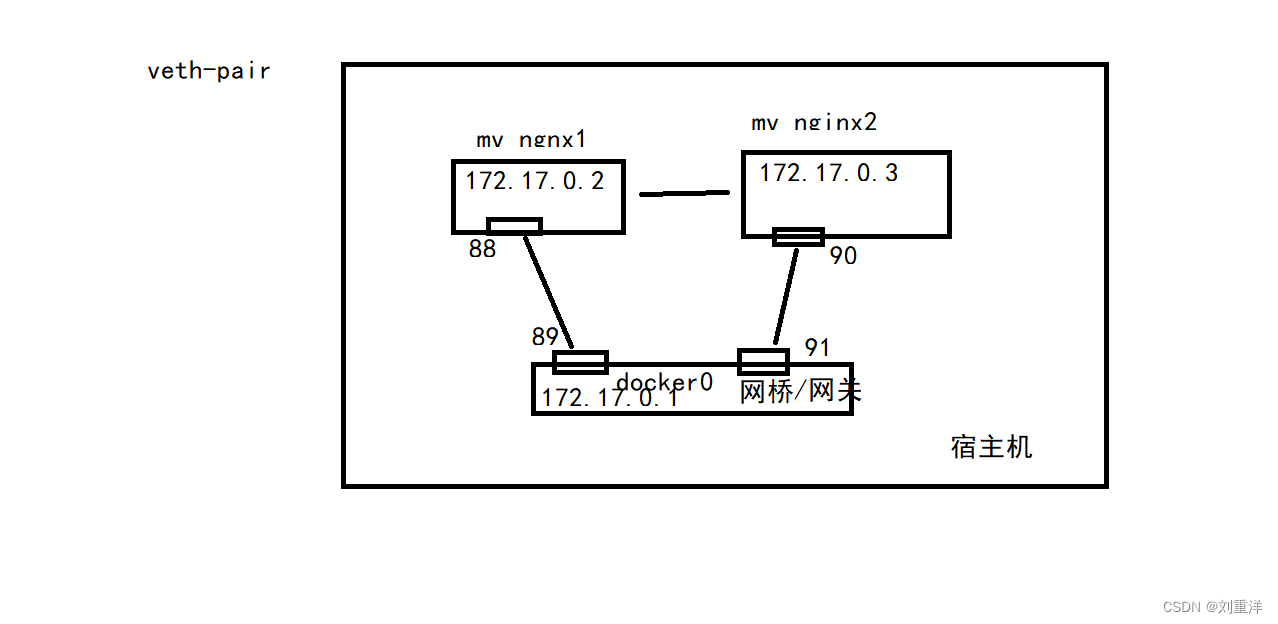
Docker实战教程 第2章 Docker基础
3-1 Docker介绍 什么是Docker 虚拟化,容器 Docker 是一个开源的应用容器引擎,基于 Go 语言 并遵从Apache2.0协议开源。 Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的 Linux 机器上&…...
)
【S32K3 MCAL配置】-3.2-CANFD配置-发送“经典CAN/CANFD标准帧“和“经典CAN/CANFD扩展帧“(基于MCAL+FreeRTOS)
"><--返回「Autosar_MCAL高阶配置」专栏主页--> 目录 实现的架构:基于MCAL层 前期准备工作: 1 评估板S32K312EVB-Q172中CAN外设...

【airtest】自动化入门教程(四)Poco元素定位
目录 一、基础操作 1、通过属性名等方式 2、通过属性组合 3、子节点方式 4、子节点加属性组合方式 5、孙节点offspring 6、兄弟节点sibling 7、父节点parent 8、正则表达式 9、直到某个元素出现 10、直到某个元素消失 二、通过局部坐标定位 1、使用局部坐标系的cli…...

Go语言中如何处理goroutine和循环变量
对goroutine和循环变量处理不当可能是Go开发人员在编写并发应用程序时最常犯的错误之一。让我们看一个具体的例子,然后我们将定义发生此类错误的条件以及如何防止发生这类错误。 在下面的示例中,我们初始化一个切片,然后在作为新goroutine执行的闭包中访问这个元素: s := …...

Pytest教程:一文了解如何使用 pytest_runtest_makereport 修改 Pytest 测试报告内容
在软件测试过程中,生成清晰、易读的测试报告对于团队交流、问题追踪和项目进度评估至关重要。Pytest 是一个功能强大的 Python 测试框架,它不仅支持丰富的断言和测试用例组织方式,还提供了灵活的插件系统和钩子函数,可以帮助我们定…...
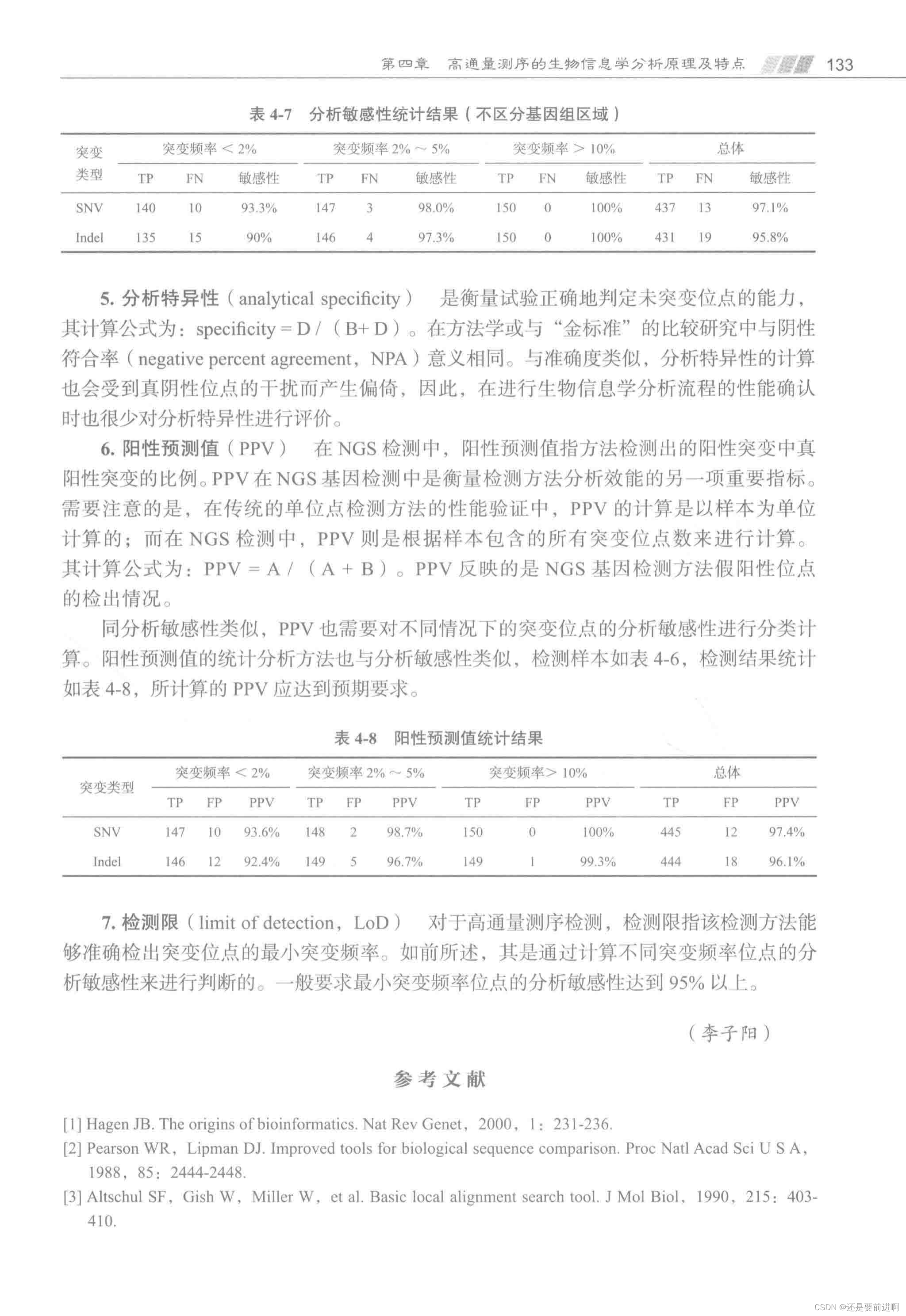
《高通量测序技术》分享,生物信息学生信流程的性能验证,以肿瘤NGS基因检测为例。
这是这本书,第四章第五节的内容,这一部分是以NGS检测肿瘤基因突变为例,描述了其原理和大概流程,这和以前我分享的病原宏基因组高通量测序性能确认方案可以互相补充,大家可以都看一下,但是想要真正的弄懂&am…...

Django+Celery框架自动化定时任务开发
本章介绍使用DjCelery即DjangoCelery框架开发定时任务功能,在Autotestplat平台上实现单一接口自动化测试脚本、业务场景接口自动化测试脚本、App自动化测试脚本、Web自动化测试脚本等任务的定时执行、调度、管理等,从而取代Jenkins上的定时执行脚本和发送…...
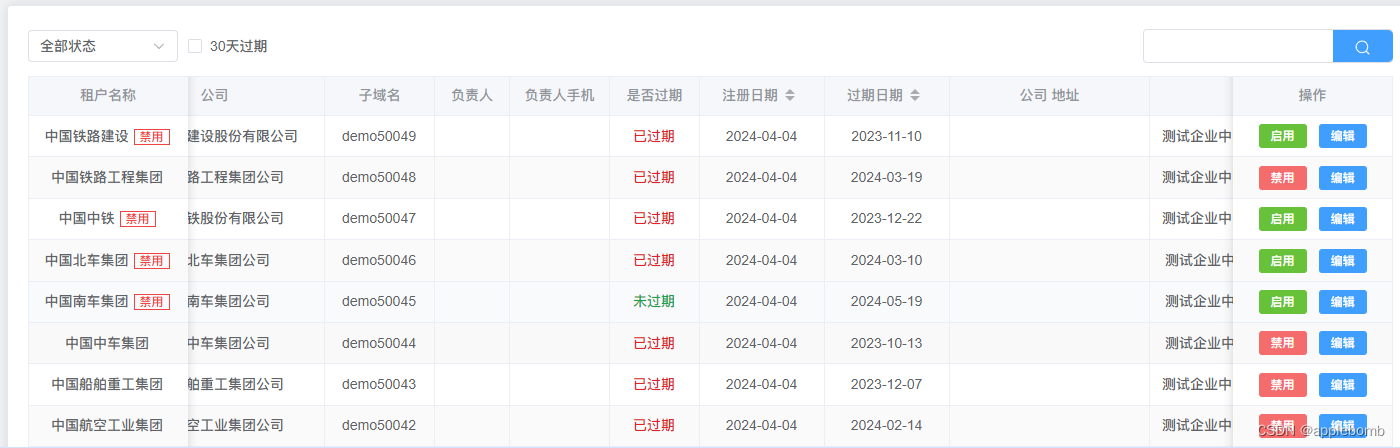
解决element-plus table组件 fixed=“right“(left)浮动后横向滚动文字穿透的问题
BUG 版本:element-plus 2.6.1 浏览器:360极速浏览器22.1 (Chromium内核) 组件:el-table组件 问题:在头部/尾部浮动加上斑马条纹后,横向滚动存在文字穿透的问题。具体如图: 白色背景行的文字,…...
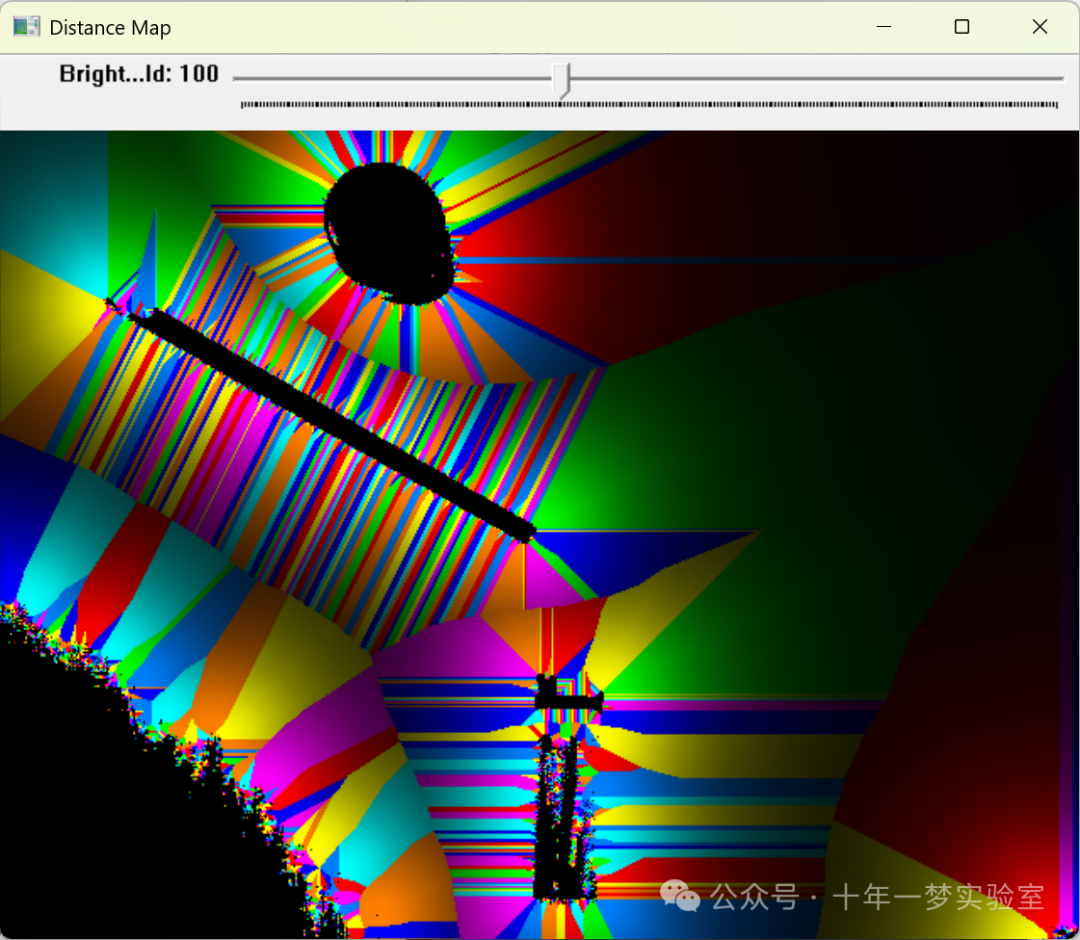
【opencv】示例-distrans.cpp 距离变换
stuff.jpg #include <opencv2/core/utility.hpp> // 包含OpenCV中的核心功能支持库 #include "opencv2/imgproc.hpp" // 包含OpenCV中的图像处理库 #include "opencv2/imgcodecs.hpp" // 包含OpenCV中的图像编解码库 #include "open…...

LVGL V8 代码细读——极致的链表使用
极致的链表的使用 序章碎碎念从redis源码里掏出来的adlist极致的精简的list.hlvgl对链表的巧思lv_ll尾记 序章碎碎念 对于链表,大家应该都不陌生。学过数据结构的,都知道它作为链式储存的基础,重要性不言而喻。 由于本人自动化专业ÿ…...
蓝桥杯第十二届c++大学B组详解
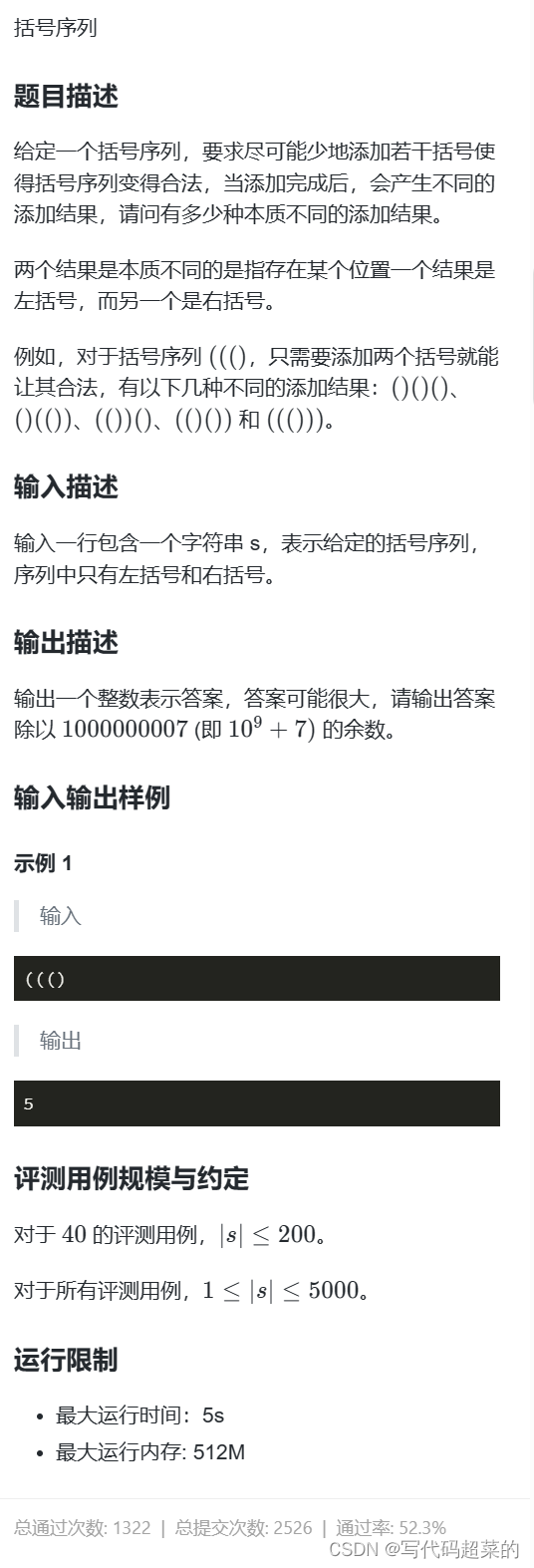
目录 1.空间 2.直线 3.路径 4.卡片 5.货物摆放 6.时间显示 7.砝码称重 8.杨辉三角 9.双向排序 10.括号序列 1.空间 题目解析:1Byte 8bit 1kb 1024B 1MB 1024kb; 先将256MB变成Byte 256 * 1024 * 1024; 再将32位 变成Byte就是 32 / 8 4;…...

Tubi 十岁啦!
Tubi 今年十岁了,这十年不可思议,充满奇迹! 从硅谷一个名不见经传的创业小作坊,转变成为四分之一美国电视家庭提供免费流媒体服务的北美领先的平台; 从费尽心力终于签下第一笔内容合作协议,到现在与 450 …...

Qt C++ 实现文件监视源码
以下是使用Qt C++实现文件监视的一个简单示例代码: #include <QCoreApplication> #include <QFileSystemWatcher> #include <QDebug>int main(int argc, char *argv[...
蓝桥杯第十一届c++大学B组详解
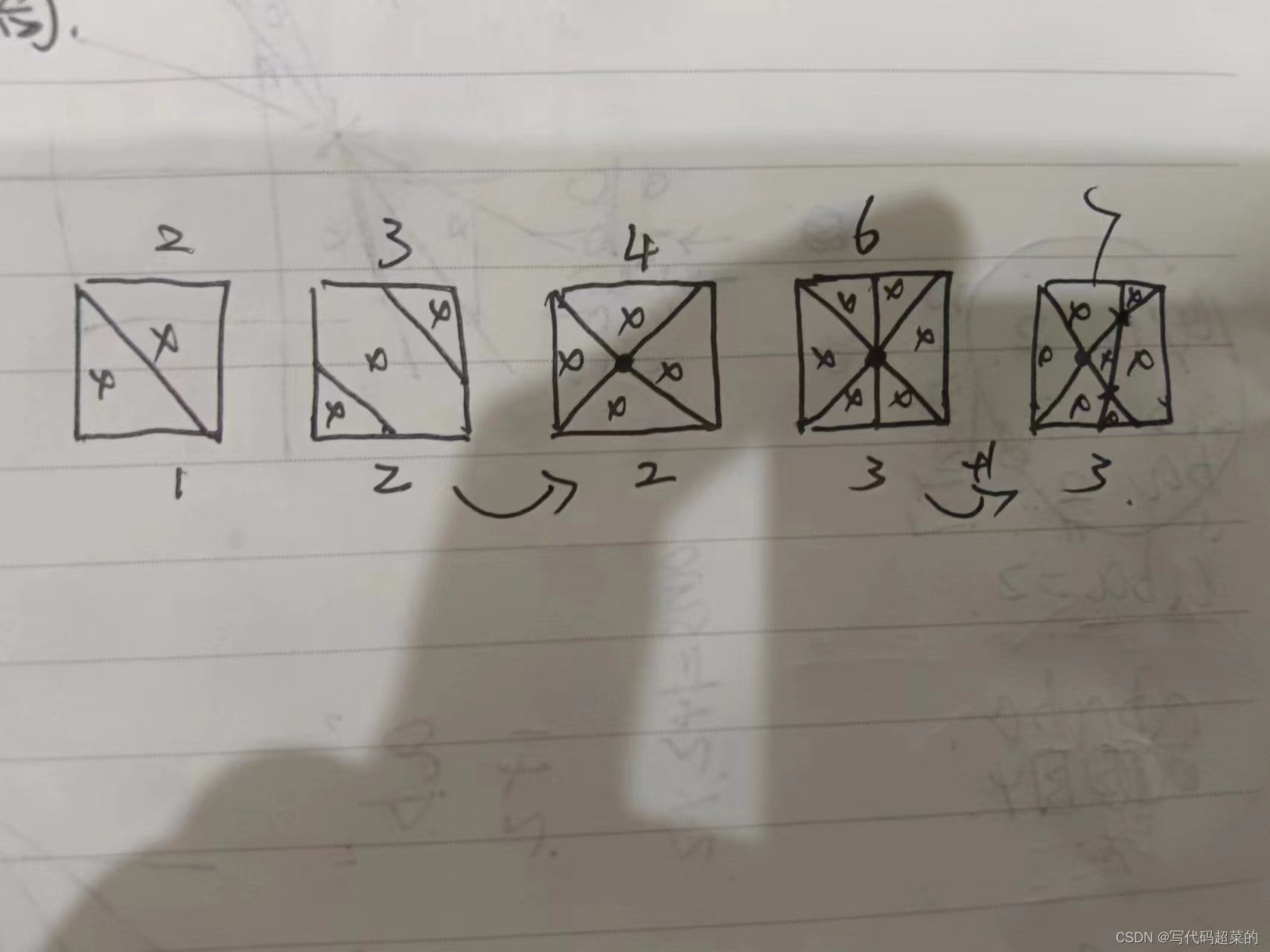
目录 1.字符串排序 2.门牌制作 3.即约分数 4.蛇型填数 5.跑步锻炼 6.七段码 7.成绩统计 8.回文日期 9.字串分值和 10.平面切分 1.字符串排序 题目解析:这个题目真没搞懂。有会的大佬教我一下谢谢。 2.门牌制作 题目解析:出过超级多这类题目&am…...

大模型日报2024-04-10
大模型日报 2024-04-10 大模型资讯 微软研究者提出通过可视化思维提升大型语言模型的空间推理能力 摘要: 微软研究者近日提出了一种新方法,旨在通过可视化思维来增强大型语言模型(LLMs)的空间推理能力。尽管LLMs在语言理解和推理任务方面表现…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...
