背包问题求方案数、具体方案
背包问题求方案数、具体方案
- 01背包问题求体积恰好等于V的方案数
- 完全背包问题求体积恰好等于V的方案数
- 01背包问题求最优选法的方案数
- 完全背包问题求最优选法的方案数
- 01背包问题求具体方案
01背包问题求体积恰好等于V的方案数
原题链接AcWing278. 数字组合
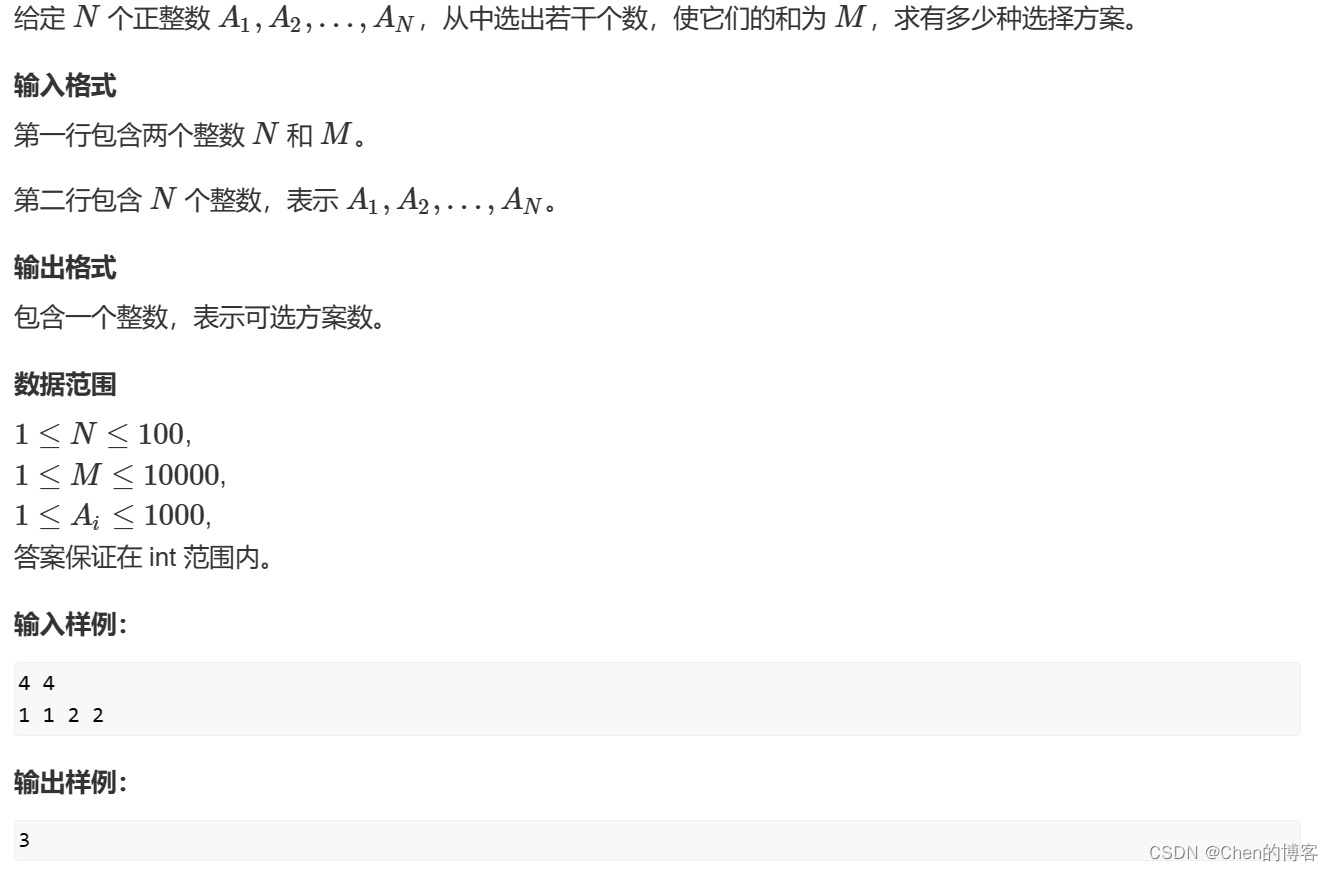
考虑状态表示:
f[i][j]表示考虑前1~i个物品,体积恰好为j时的方案数(不考虑前1~i个物品组合后的价值,只考虑组合后的体积)状态转移:
可以分两种情况
选第i个物品使得体积为j
不选第i个物品使其体积为j
第i个物品体积为v,价值为w可以发现f[i][j]由上述两种情况构成,所以
f[i][j]=f[i-1][j]+f[i-1][j-v]
因为是体积恰好是j,所以初始化时
memset(f,0,sizeof f)
f[0][0]=1;
再对空间复杂度进行优化
代码如下:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=10010;
int f[M];//f[i][j]表示考虑前1~i个物品,体积恰好为j时的方案数int main(){int n,m;cin>>n>>m;f[0]=1;for(int i=0;i<n;i++){int v;scanf("%d",&v);for(int j=m;j>=v;j--)f[j]=f[j]+f[j-v];}cout<<f[m]<<endl;return 0;
}
完全背包问题求体积恰好等于V的方案数
原题链接AcWing 1023. 买书

物品数量无限,这是一道完全背包求方案数问题
考虑状态表示:
f[i][j]表示考虑前1~i个物品,体积恰好为j时的方案数(不考虑前1~i个物品组合后的价值,只考虑组合后的体积)状态转移:
可以分多种情况
不选第i个物品使其体积为j f[i-1][j]
选1个第i个物品使得体积为j f[i-1][j-v]
选2个第i个物品使得体积为j f[i-1][j-2*v]
.....
选s个第i个物品使得体积为j f[i-1][j-s*v]
第i个物品体积为v,价值为w可以发现f[i][j]由上述s+1种情况构成,所以
f[i][j]=f[i-1][j]+f[i-1][j-v]+f[i-1][j-2*v]+.....+f[i-1][j-s*v]
而
f[i][j-v]=f[i-1][j-v]+f[i-1][j-2*v]+.....+f[i-1][j-s*v]
所以
f[i][j]=f[i-1][j]+f[i][j-v]
因为是体积恰好是j,所以初始化时
memset(f,0,sizeof f)
f[0][0]=1;
再对空间复杂度进行优化
代码如下:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1010;
int f[N];
int d[4]={10,20,50,100};
int main(){int n;cin>>n;f[0]=1;for(int i=0;i<4;i++)for(int j=d[i];j<=n;j++)f[j]+=f[j-d[i]];cout<<f[n];return 0;
}
01背包问题求最优选法的方案数
AcWing 11. 背包问题求方案数

考虑状态表示:
f[i][j]表示考虑前1~i个物品, 体积恰好为j时的最大价值
g[i][j]表示考虑前1~i个物品,体积恰好为j时(最大价值)时的方案数状态转移:
可以分两种情况
选第i个物品使得体积为j
不选第i个物品使其体积为j
第i个物品体积为v,价值为w可以发现f[i][j]由上述两种情况构成,所以
f[i][j]=max(f[i-1][j],f[i-1][j-v]+w)
f[i-1][j]==f[i-1][j-v]+w时,g[i][j]=g[i-1][j-v]+g[i-1][j]//选不选i都行,可以从两种状态转移而来
f[i-1][j]<f[i-1][j-v]+w时,g[i][j]=g[i-1][j-v]//考虑要求最大价值时的方案数,只能从一种状态转移而来
f[i-1][j]>f[i-1][j-v]+w时,g[i][j]=g[i-1][j]//考虑要求最大价值时的方案数,只能从一种状态转移而来
因为是体积恰好是j,所以初始化时
memset(f,-0x3f,sizeof f)
f[0][0]=1;
memset(g,0,sizeof g)
g[0][0]=1;
再对空间复杂度进行优化因为求得的是在每个体积的最大价值,不同的体积可能有相同的最大价值,
最后需要将所有有最大价值不同体积方案数累加求和
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N];
int g[N];
int main(){int n,m;cin>>n>>m;memset(f,-0x3f,sizeof f);//求体积恰好等于j的最大价值f[0]=0;g[0]=1;//求体积恰好等于j的最大方案数for(int i=0;i<n;i++){int v,w;scanf("%d%d",&v,&w);for(int j=m;j>=v;j--){int cnt;if(f[j]<f[j-v]+w) cnt=g[j-v];else if(f[j]==f[j-v]+w) cnt=g[j-v]+g[j];else cnt=g[j];g[j]=cnt%mod;f[j]=max(f[j],f[j-v]+w);}}int res=0;for(int i=0;i<=m;i++) res=max(res,f[i]);//找出最大价值int cnt=0;for(int i=0;i<=m;i++) //找出所有体积不同的最大价值,每个体积有不同的方案数,累加求和if(f[i]==res) cnt=(cnt+g[i])%mod;cout<<cnt<<endl;return 0;
}
完全背包问题求最优选法的方案数
从上面的几个例子我们也可以求出完全背包问题最大价值时的方案数
没有例题
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N];
int g[N];
int main(){int n,m;cin>>n>>m;memset(f,-0x3f,sizeof f);//求体积恰好等于j的最大价值f[0]=0;g[0]=1;//求体积恰好等于j的最大方案数for(int i=0;i<n;i++){int v,w;scanf("%d%d",&v,&w);for(int j=v;j<=m;j++){//改动在这里int cnt;if(f[j]<f[j-v]+w) cnt=g[j-v];else if(f[j]==f[j-v]+w) cnt=g[j-v]+g[j];else cnt=g[j];g[j]=cnt%mod;f[j]=max(f[j],f[j-v]+w);}}int res=0;for(int i=0;i<=m;i++) res=max(res,f[i]);//找出最大价值int cnt=0;for(int i=0;i<=m;i++) //找出所有体积不同的最大价值,每个体积有不同的方案数,累加求和if(f[i]==res) cnt=(cnt+g[i])%mod;cout<<cnt<<endl;return 0;
}
应该是对的
01背包问题求具体方案
原题链接:AcWing 12. 背包问题求具体方案

01背包求具体方案只需要回溯输出结果就行
因为我们可以知道当前这一状态是从哪一个状态转移而来
因为题目要求字典序最小,所以可以反着算,正着回溯输出即可
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010;int f[N][N];
int v[N],w[N];int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++)scanf("%d%d",&v[i],&w[i]);for(int i=n;i>=1;i--)for(int j=0;j<=m;j++){f[i][j]=f[i+1][j];if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);}for(int i=1,j=m;i<=n;i++)if(j>=v[i] && f[i][j]==f[i+1][j-v[i]]+w[i]){cout<<i<<" ";j-=v[i];}return 0;
}
相关文章:

背包问题求方案数、具体方案
背包问题求方案数、具体方案01背包问题求体积恰好等于V的方案数完全背包问题求体积恰好等于V的方案数01背包问题求最优选法的方案数完全背包问题求最优选法的方案数01背包问题求具体方案01背包问题求体积恰好等于V的方案数 原题链接AcWing278. 数字组合 考虑状态表示&#x…...

电商导购CPS,淘宝联盟如何跟单实现用户和订单绑定
前言 大家好,我是小悟 做过自媒体的小伙伴都知道,不管是发图文还是发短视频,直播也好,可以带货。在你的内容里面挂上商品,你自己都不需要囤货,如果用户通过这个商品下单成交了,自媒体平台就会…...
【Shell1】shell语法,ssh/build/scp/upgrade,环境变量,自动升级bmc,bmc_wtd,
文章目录1.shell语法:Shell是用C语言编写的程序,它是用户使用Linux的桥梁,硬件>内核(os)>shell>文件系统1.1 变量:readonly定义只读变量,unset删除变量1.2 函数:shell脚本传递的参数中包含空格&am…...

刷题记录:牛客NC208250牛牛的最美味和最不美味的零食
传送门:牛客 题目描述: 牛牛为了减(吃)肥(好),希望对他的零食序列有更深刻的了解,所以他把他的零食排成一列,然后对每一 个零食的美味程度都打了分,现在他有可能执行两种操作&…...
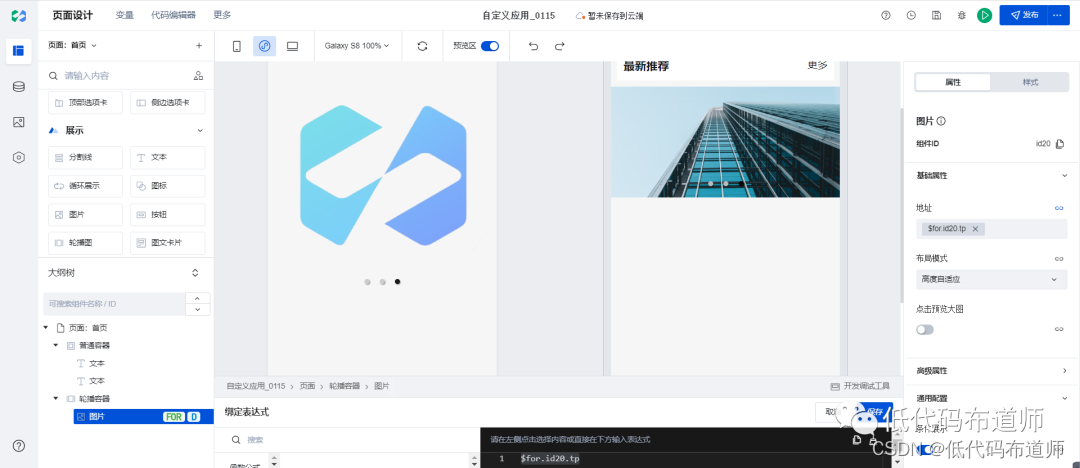
微搭低代码从入门到精通08-轮播容器
我们上一篇讲解了基础布局组件,讲解了普通容器和文本组件的用法,本篇我们继续介绍布局组件。 小程序中经常会有个功能是轮播图展示的功能,多张图片可以顺序进行切换。我们学习使用轮播容器的时候,先考虑切换的图片从哪来…...
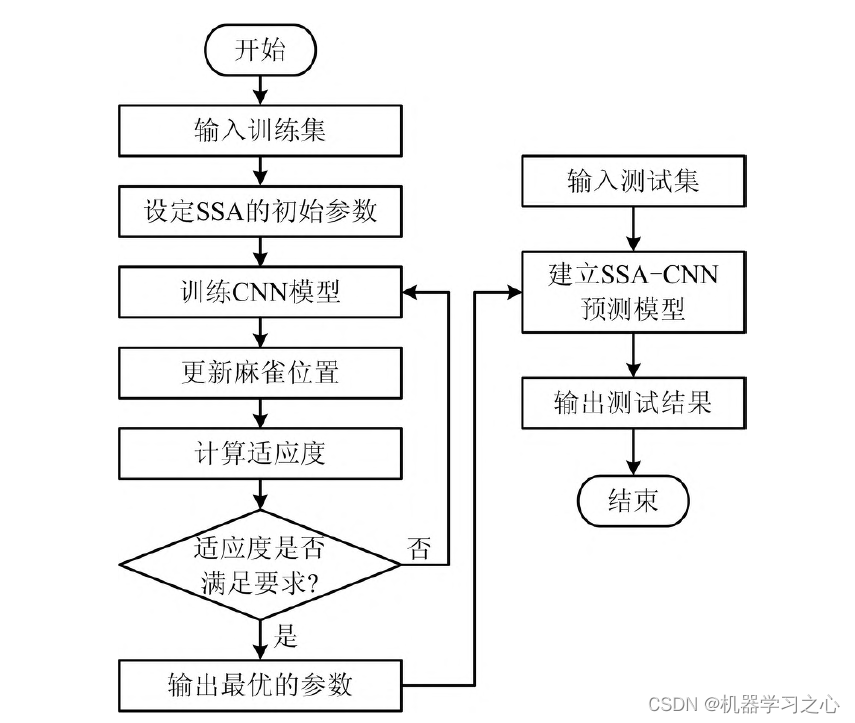
分类预测 | MATLAB实现SSA-CNN麻雀算法优化卷积神经网络多特征分类预测
分类预测 | MATLAB实现SSA-CNN麻雀算法优化卷积神经网络多特征分类预测 目录分类预测 | MATLAB实现SSA-CNN麻雀算法优化卷积神经网络多特征分类预测分类效果基本介绍模型描述程序设计参考文献分类效果 基本介绍 1.Matlab实现SSA-CNN麻雀算法优化卷积神经网络多特征分类预测&…...

华为10年经验测试工程师,整理出来的python自动化测试实战
前言 全书共分11章,第一章是基础,了selenium家谱,各种组件之间的关系以及一些必备知识。第二章告诉如何开始用python IDLE写程序以及自动化测试环境的搭建。第三章是webdriver API,我花了相当多时间对原先的文档,冗余…...

OpenCV杂谈 - 如何导出图像到内存中其他结构
前言 最近在net环境使用OpenCV,记录些疑难杂点. 一、OpenCV主要结构 Mat 二、Cols,Rows 和 Width,Hight 三、导入\导出到内存中其他结构 四、按矩形 在Mat之间复制 总结 一、OpenCV主要结构 Mat Mat是OpenCV中的主要结构. 主要有两个用途. 1 存储图片信息,2 存…...
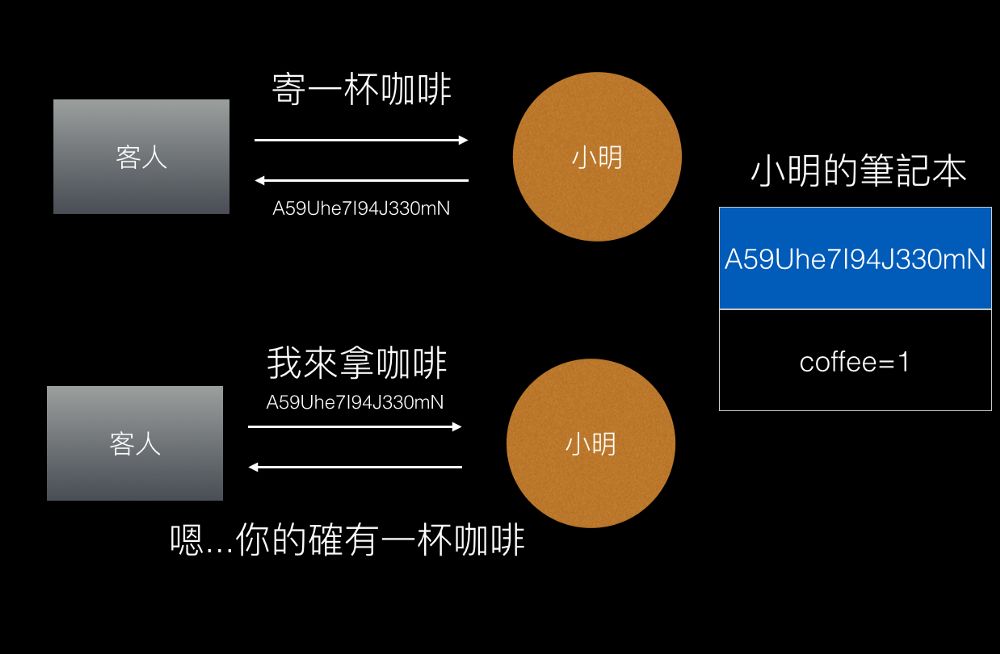
Session与Cookie的区别(四)
咖啡寄杯的烦恼 虽然店里生意还可以,但小明无时无刻不想着怎么样发大财赚大钱,让店里的生意变得更好。 他观察到最近好多便利商店开始卖起了咖啡,而且时不时就买一送一或是第二件半价,并且贴心地提供了寄杯的服务。 寄杯就是指说你…...

Linux 文件锁 - fcntl
什么是文件锁? 即锁住文件,不让其他程序对文件做修改! 为什么要锁住文件? 案例,有两个程序,都对一个文件做写入操作。 #include <unistd.h> #include <stdio.h> #include <stdlib.h> …...

CellularAutomata元胞向量机-2-初等元胞自动机MATLAB代码分享
%% 二维元胞自动机%imagesc(a)的色度矩阵a中0->256由蓝变黄% 规则,先把中间点置为1,每一时间每一点如果%周围八个点和为偶数,则变为0,为奇数则变为 1% 颜色控制clc, clearMap [1 1 1; 0 0 0];% [0 0 0] is black, [1 1 1] is …...
 | 部署Neutron)
OpenStack云平台搭建(6) | 部署Neutron
目录 1.在控制节点登录数据库配置 2.要创建服务证书,完成这些步骤 3.创建网络服务API端点: 4.安装网络组件 5.配置neutron组件 6.配置 Modular Layer 2 (ML2) 插件 7.配置Linuxbridge代理 8.配置DHCP代理 9.配置元数据代理 10.编辑/etc/nova/no…...

Lesson 05.Configuring the Oracle Network Environment
Lesson 05. Configuring the Oracle Network Environment 文章目录Lesson 05. Configuring the Oracle Network Environment1. 监听程序的配置文件有哪些,如何命名,保存在什么位置?2. Oracle 网络的服务名称文件是如何命名的,需要…...

理论五:接口vs抽象类的区别,如何用普通的类模拟抽象类和接口
在面向对象编程中,抽象类和接口是两个经常被用到的语法概念,是面向对象四大特性,以及很多设计模式、设计思想、设计原则编程实现的基础。比如,我们可以使用接口来实现面向对象的抽象特性、多态特性和基于接口而非实现的设计原则,使用抽象类来实现面向对象的继承特性和模板设计模…...
【Hello Linux】 Linux的权限以及Shell原理
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:介绍Linux的基础命令 Linux的权限以及Shell原理Shell的运行原理权限Linux中权限的概念如何切换用户如何提升当前操作的权限如何添加信任…...
【STM32】【HAL库】遥控关灯2 分机
相关连接 【STM32】【HAL库】遥控关灯0 概述 【STM32】【HAL库】遥控关灯1主机 【STM32】【HAL库】遥控关灯2 分机 【STM32】【HAL库】遥控关灯3 遥控器 需求 接收RF433和红外信号,根据信号内容控制舵机 硬件设计 主控采用stm32F103c6 STM32 433接收 其他接口 软件设计 接…...

代码随想录算法训练营第27天|● 93.复原IP地址 ● 78.子集 ● 90.子集II
93.复原IP地址 看完题后的思路 典型分割问题略lue略剪枝条件 sub: 1) 不是一位首字母为0 2)大于三位 3)介于0-255之间 4) 当已分割得到3个时,第四个直接从startIndex到末尾就行 代码 ArrayList<String> slist…...

Unity UI合批的问题
今天看到一个问题,主要说的是Unity中的UI资源合批的问题之前一直以为主要和UI资源在Hierarchy中的排列顺序有关,但其实这并不是最主要的,因为Unity会对同一个Canvas下的UI进行排序(注:不同Canvas下的资源是不能够合批的…...
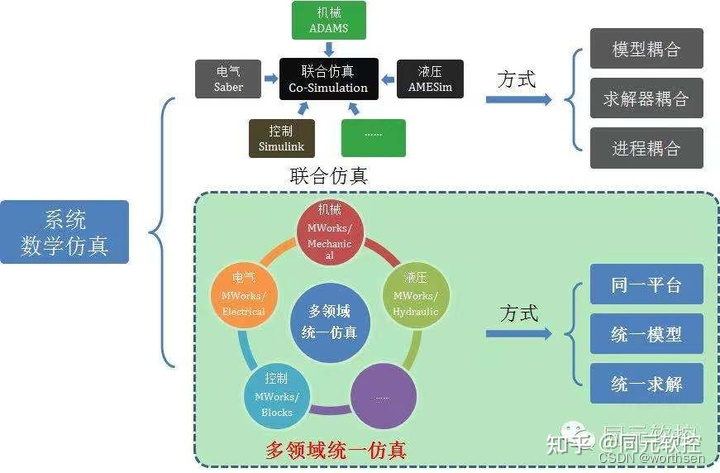
MWORKS--系统建模与仿真
MWORKS--系统建模与仿真1 系统定义特征2 系统研究2.1 特点与原则2.2 方法百度百科归纳同元杠归纳3 系统建模与仿真3.1 系统、模型、仿真的关系3.2 系统建模4 建模方法4.1 方法4.2 一般流程4.3 目的5 仿真方法5.1 方法5.2 流程参考1 系统定义 系统是由相互作用相互依赖的若干组…...

PC端开发GUI
PC端开发GUI 一、搭建PC端环境:常规方式1、Python2、Pycharm二、搭建PC端环境:创建虚拟环境1、创建文件夹存放虚拟环境相关2、配置环境变量3、创建.ui文件4、.ui文件转成.py文件5、打包.py文件来发布.exe一、搭建PC端环境:常规方式 1、Python 注意Python版本不能超过3.9,…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...
