数据结构—二叉树、完全二叉树的性质
# 1
若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2,则该树的总结点个数是多少?
正确答案:
答案:结点总数n=n0+n1+n2+n3+n4,又由于除根结点外,每个结点都对应一个分支,所以总的分支数等于n-1。而度为i(0≤i≤4)的结点的分支数为i,所以有:总分支数=n-1=0×n0+1×n1+2×n2+3×n3+4×n4。综合两式得:n0=n2+2n3+3n4+1=3+2×2+3×2=14,则n=n0+n1+n2+n3+n4=14+4+3+2+2=25,所以该树的总结点个数是25。
我的答案:
由树的性质,树的总结点个数为树的总度数+1
所以总结点个数为8+6+6+4+1 = 25
# 2
若一棵度为4的树中度为2、3、4的结点个数分别为3、2、2,总结点个数为25,则该树中度为1的结点个数是多少?
正确答案:
答案:结点总数n=n0+n1+n2+n3+n4,又由于除根结点外,每个结点都对应一个分支,所以总的分支数等于n-1。而度为i(0≤i≤4)的结点的分支数为i,所以有:总分支数=n-1=0×n0+1×n1+2×n2+3×n3+4×n4。综合两式得:n0=n2+2n3+3n4+1=3+2×2+3×2=14,则n=n0+n1+n2+n3+n4,n1=n-n0-n2-n3-n4=25-14-3-2-2=4,所以该树中度为1的结点个数是4。
我的答案:
设度为1的结点个数为x
由树的性质总结点个数等于总度数+1得方程2 x+2*3+3*2+4*2 +1= 25
解得x = 4
所以度为1的结点个数是4
# 3
对于度为m的树T,其高度为h,则最少的结点个数和最多的结点个数分别是多少?
正确答案:
答案:第i层最多有mi-1个结点,所以最多结点个数=1+m+m2+…+mh-1=(mh-1)/(m-1)。
最少结点的情况是:某一层有m个结点,其他每层只有一个结点,此时结点个数=m+(h-1)=m+h-1。
我的答案:
最少有m+h-1个
最多有(m^h-1)/(m-1)个
4
对于含有n个结点的m次树,采用孩子链存储结构时,其中空指针域的个数有多少?
正确答案:
答案:该m次树中有n个结点,采用孩子链存储结构时,每个结点有m个指针,总指针域个数=m×n。又由于分支数=n-1,而每个分支是由一个非空指针域引出的,所以总的非空指针域个数=n-1,因此,空指针域的个数=总指针域个数-空指针域的个数=m×n-(n-1)=n(m-1)+1。
我的答案:
对于m次树,它的非空指针域就等于它的边数等于结点个数-1,所以非空指针域有 n-1个
总的指针域有nm个
所以空指针域 = 总指针域 - 非空指针域
空指针域的个数有 nm - (n-1) = n(m-1)+1
# 5
任意一个有n个结点的二叉树,已知它有m个叶子结点,试证明有(n-2m+1)个度数为1的结点。
正确答案:
答案:
证明:设n1为二叉树中度为1的结点数,n2为度2的结点数,则总的结点数为:
n=n1+n2+m
根据二叉树的性质1可知n0=n2+1,即n2=n0-1=m-1,所以有n=n1+n2+m=n1+2m-1,则n1=n-2m+1。
我的答案:
度数之和等于分支数
因为在二叉树中 :
度数之和 = n1 + 2n2
n0 = n2 + 1
分支数 = n - 1
n = n0 + n1 + n2
所以 n0 = m = n2 + 1
所以n1 = n- m- n2 = n - m + 1 = n - 2m +1
# 6
为什么说一棵非空完全二叉树,仅已知叶子结点个数n0,其树形是不能确定的。
正确答案:
答案:
由完全二叉树的特性可知,一旦结点个数n确定了,其树形也就确定了。当只有n0已知时,n2=n0-1,n=n0+n1+n2=2n0-1+n1,而n1可以为0或1,也就是说,n=2n0-1或n=2n0,其结点总数不确定,所以该完全二叉树的形态是不能确定的。
我的答案:
因为如果对于只有一个结点和有两个结点的完全二叉树来说,这两棵树都只有一个叶子结点,即n0 = 1,但树形不一样,所以,对于一棵非空完全二叉树,仅已知叶子结点数n0,树形是不确定的
相关文章:

数据结构—二叉树、完全二叉树的性质
# 1 若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2,则该树的总结点个数是多少? 正确答案: 答案:结点总数nn0n1n2n3n4,又由于除根结点外,每个结点都对应一个分支,所以总的分支数等…...
JDBC编程复习
文章目录JDBC1.概念2.原理3. 如何使用JDBC编程1. 下载mysql的jdbc驱动2. 项目中引入驱动4. JDBC使用1. 和数据库建立连接2.获取连接3. Statement对象4. 释放资源JDBC 1.概念 JDBC,即Java Database Connectivity,java数据库连接。是Java提供的API用来执行SQL语句&a…...
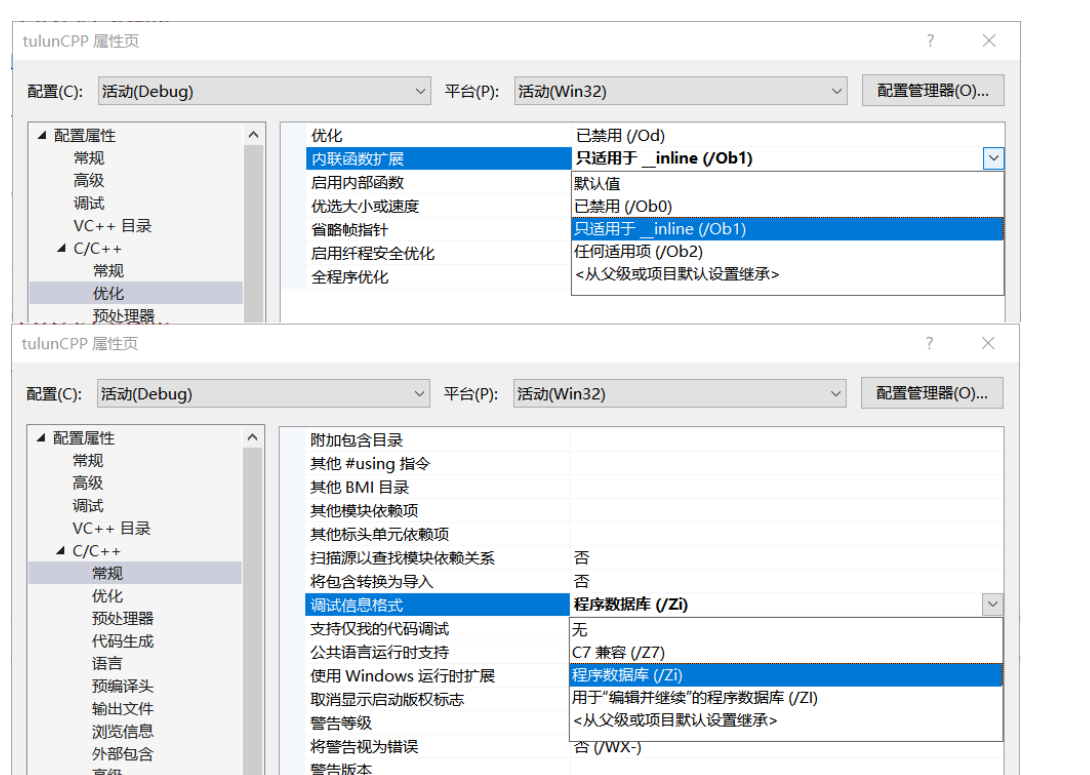
c++基础入门二
一、数组的引用int main() {int a 10, b 20;int ar[10] { 1,2,3,4,6,7 };int& x ar[0];int& p[5] ar;//errorint(&p)[10] ar;//引用整个数组的大小sizeof(ar)int(*p)[10] &ar;//typesize表示整个数组//只有在这三种情况下代表整个数组,其他情…...
企业数字化转型的产品设计思路
数字化转型的核心是全面重塑企业的管理模式和经营模式,是迈向数字经济时代的方式。一、到底什么是数字化转型?数字化转型并不神秘。数字化转型是一种经营方式、一种经营理念,是将企业相关的人、物料、设备、资金等要素进行系统运转࿰…...

Linux日志分析常用命令
一:常用命令1、tail参数: tail [ -f ] [ -c Number | -n Number | -m Number | -b Number | -k Number ] [ File ] 参数说明: -f 该参数用于监视File文件增长。 -c Number 从 Number 字节位置读取指定文件 -n Number 从 Number 行位置读取指…...
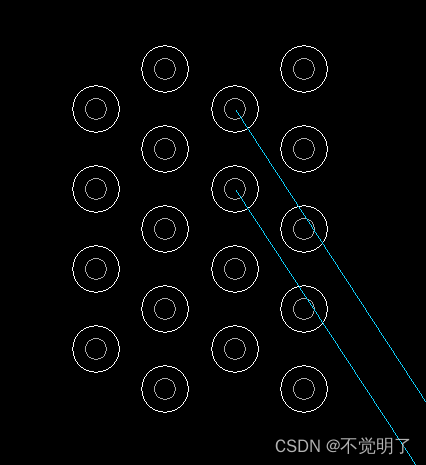
Allegro如何使用Snake命令走蛇形线操作指导
Allegro如何使用Snake命令走蛇形线操作指导 在做PCB设计的时候,遇到不规则BGA的时候,蛇形走线是惯用的走线方式,类似下图 Allegro支持蛇形走线,具体操作如下 首先把过孔打好,尽量上下左右间距一致,不容易出现偏差,如下图在Command命令栏下方输入snake,然后回车...

在 Eclipse 中创建 Maven 项目
1.在 Eclipse 中配置 MavenEclipse 中默认自带 Maven 插件,但是自带的 Maven 插件不能修改本地仓库,所以通常我们不使用自带的 Maven ,而是使用自己安装的,在 Eclipse 中配置 Maven 的步骤如下: 1) 点击 Eclipse 中的 …...

flex 布局相关属性的使用
简单概述 为元素添加 display:flex; 的属性后,当前元素被视为弹性布局的盒子容器(box),其子元素被视为弹性布局项目(item)。item 会在 box 内灵活布局,解决了对齐、分布、尺寸等响应式问题。 演示 demo <template><div class&quo…...

【C++】类和对象(第一篇)
文章目录1. 面向过程和面向对象初步认识2.类的引入3.类的定义3.1 类的两种定义方式3.2 成员变量命名规则建议4. 类的访问限定符及封装4.1 访问限定符4.2 封装5. 类的作用域6. 类的实例化7. 类对象模型7.1 类对象大小的计算7.2 类对象的存储方式猜测7.3 结构体内存对齐规则复习8…...

springboot 接入websocket实现定时推送消息到客户端
目录说明代码实现说明 如标题,举例需求场景: 前端与后端websocket连接上后,多用户登录,后端根据不同用户定时发消息给前端用于展示 代码实现 1、 <dependency><groupId>org.springframework.boot</groupId>…...
虚拟机磁盘重新分区增加Docker磁盘空间
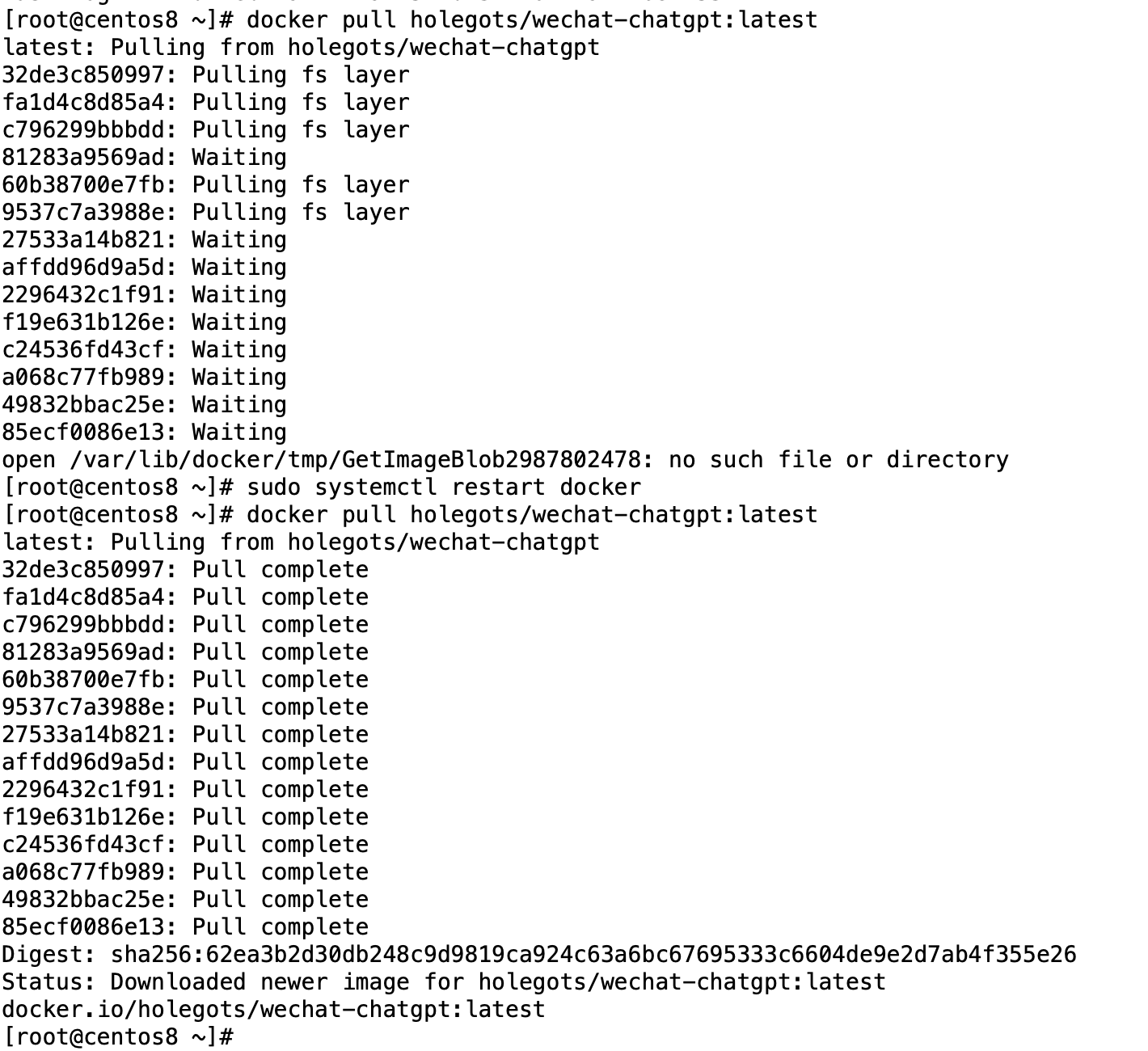
目录一、简介二、重新分区 挂载目录2.1 增加虚拟机硬盘空间2.2 重新分区2.3 格式化新分区2.4 挂载docker目录三、重新拉取一、简介 今天在使用docker pull 拉取镜像时,报了no such file or directory的信息,原来是Docker的磁盘空间满了 #查看Docker Roo…...
Java开发学习(四十八)----MyBatisPlus删除语句之逻辑删除
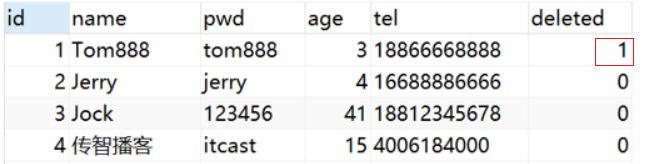
1、逻辑删除 接下来要讲解是删除中比较重要的一个操作,逻辑删除,先来分析下问题: 这是一个员工和其所签的合同表,关系是一个员工可以签多个合同,是一个一(员工)对多(合同)的表 员工ID为1的张业绩,总共签了三个合同&a…...
RabbitMq
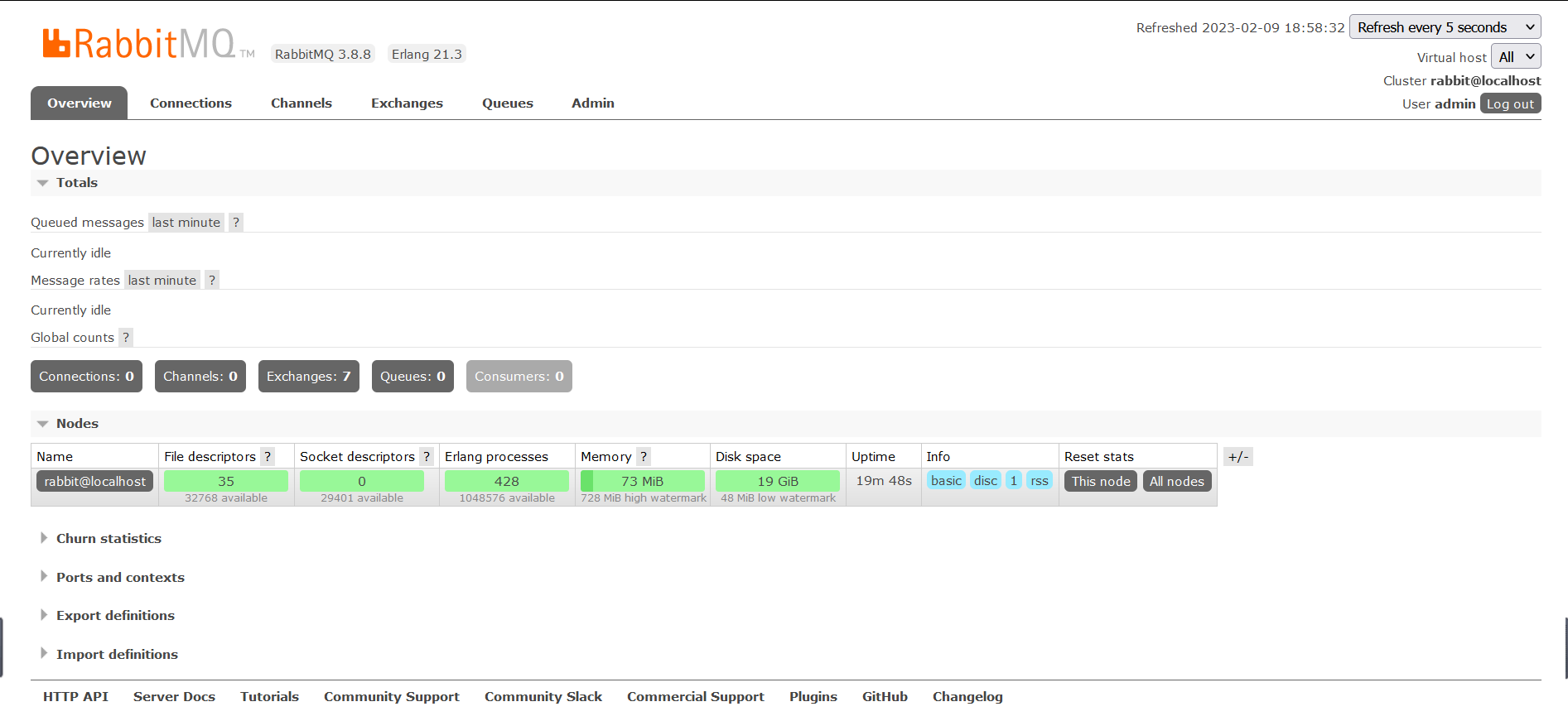
一、四大核心概念生产者:产生数据发送消息的程序是生产者交换机:交换机是RabbitMQ非常重要的一个部件,一方面它接收来自生产者的消息,另一方面它将消息推送到队列中。交换机必须确切知道如何处理它接收到的消息,是将这…...
Qt学习笔记
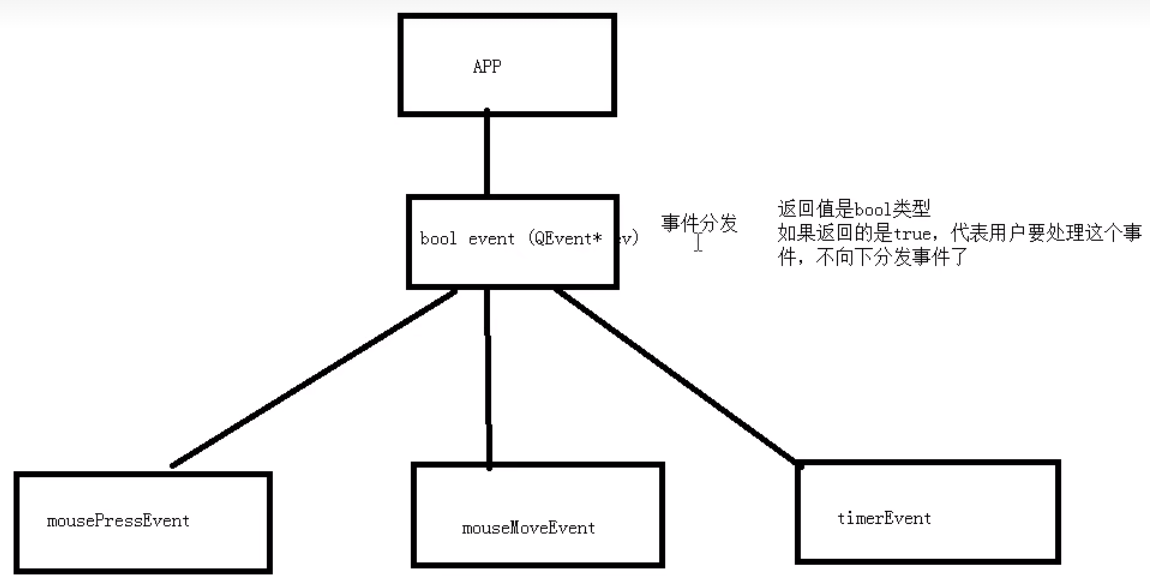
文章目录一、C指针函数驼峰命名法、下划线命名法编程报错二、C三、Qt语法Qt历史、Qt应用Qt特色快捷键Qt类的族谱QWidgetQPushButtonQDebug对象树Qt窗口坐标信号和槽Qt自带的信号的槽自定义的信号和槽Qt4版本 vs Qt5版本 的connect写法函数指针解决重载问题拓展类型转换QString …...
洛谷——P1091 合唱队形
【题目描述】 n 位同学站成一排,音乐老师要请其中的 n−k 位同学出列,使得剩下的 k 位同学排成合唱队形。 合唱队形是指这样的一种队形:设 kk 位同学从左到右依次编号为 1,2, … ,k,他们的身高分别为,, … ,,则…...
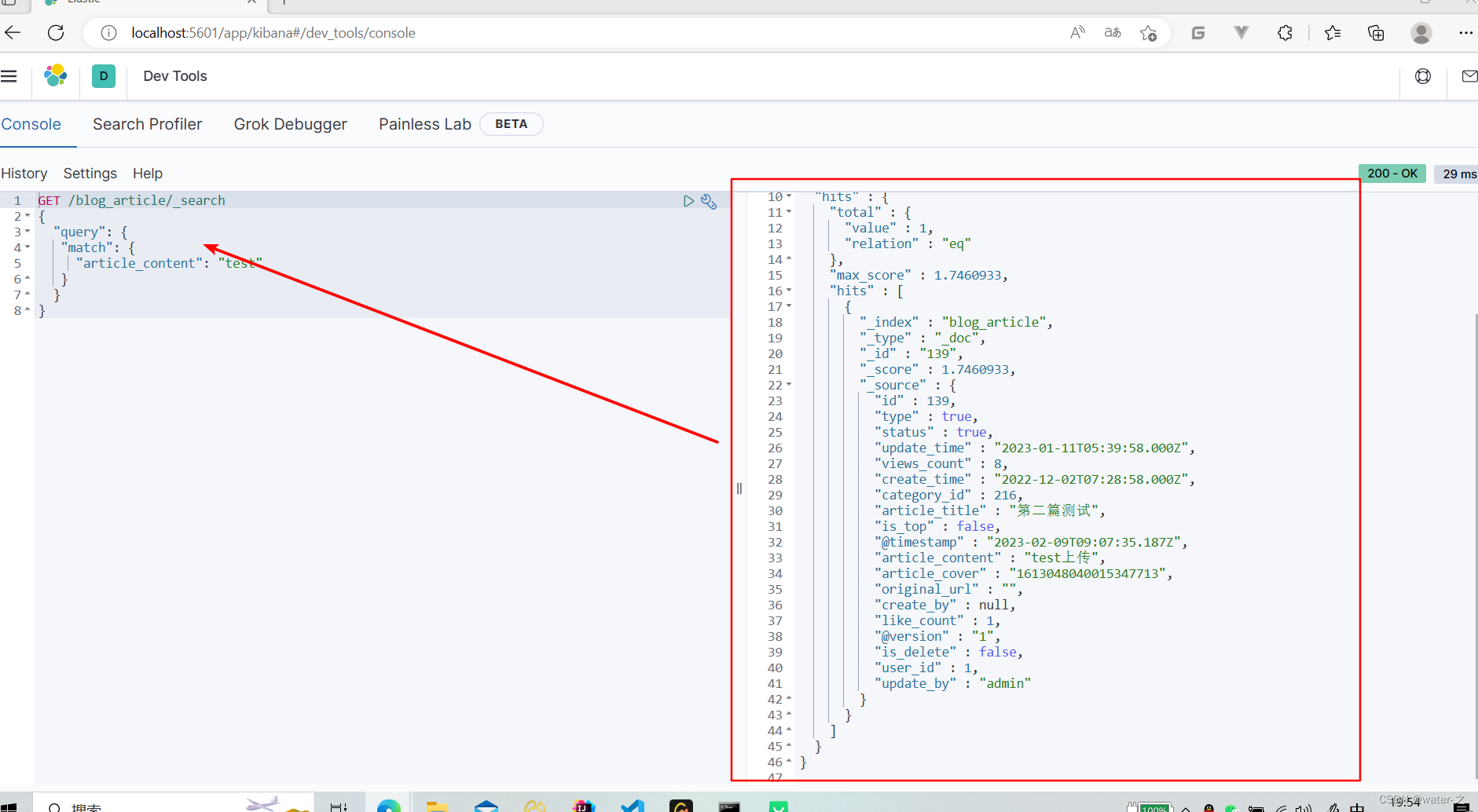
使用logstash把mysql同步到es,Kibana可视化查看
1:首先需要电脑本地有es环境,并且要牢记版本后,后续安装的logstash和Kibana一定要版本对应 查看es版本:http://localhost:9200/ 2:安装对应版本的logstash:找到自己对应ES版本,然后解压 Logst…...

Vue3.0 setup的使用及作用
目录开篇:1.什么是setup2.setup怎么使用3.setup中包含的生命周期函数3.setup相关参数4.setup特性总结总结开篇: 从vue2升级 vue3,vue3是可以兼容vue2。所以v3可以采用v2的选项式api,但是v2不能使用v3的组合式api,由于…...

Ubuntu18.04安装Vertica
目录下载安装包安装(Ubuntu18.04)配置 I/O Scheduler配置 TZSupport Tools配置 swapinessDisk ReadaheadEnabling chrony or ntpd自启动项错误处理后重装下载安装包 官网11.0版本或者10.0(deb)安装包可私信提供百度网盘链接; 安装(Ubuntu18.04) testvertica:~$ s…...
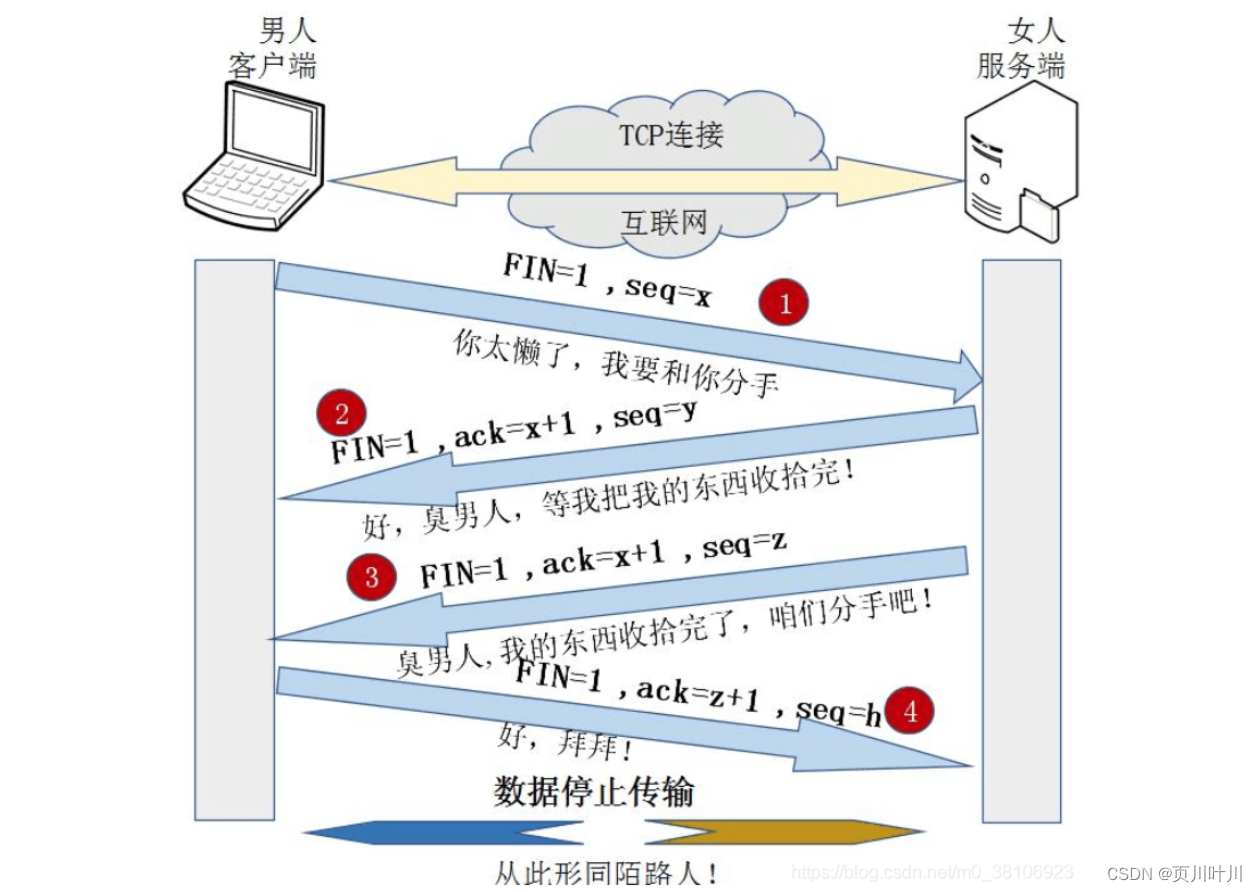
2.计算机基础-计算机网络面试题—基础知识、容器、面向对象、并发编程
本文目录如下:计算机基础-计算机网络 面试题一、基础知识简述 TCP 和 UDP 的区别?http与https的区别?Session 和 Cookie 有什么区别?URL是什么?由哪些部分组成?OSI 的 五层模型 都有哪些?get 和 post 请求…...
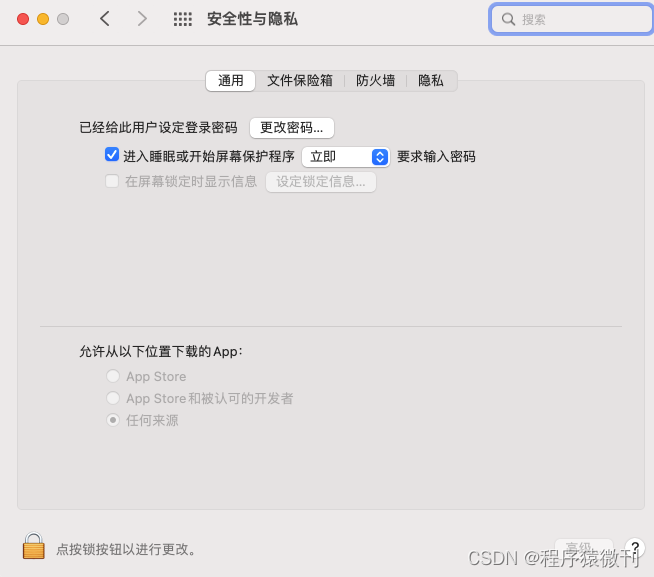
解决Mac 安装应用提示:xx已损坏,无法打开。 您应该将它移到废纸篓问题
许多新手mac 用户安装应用得时候会出现 “已损坏,无法打开。您应该将它移到废纸娄” 导致无法正常安装,其实应用软件b并没有损坏,只是系统安全设置,我们改如何解决呢? 1、开启允许任何来源 苹果已经取消了允许“任何…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
