洛谷——P1091 合唱队形
【题目描述】
n 位同学站成一排,音乐老师要请其中的 n−k 位同学出列,使得剩下的 k 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 kk 位同学从左到右依次编号为 1,2, … ,k,他们的身高分别为,
, … ,
,则他们的身高满足
<……<
>……>
(1≤i≤k)。
你的任务是,已知所有 n 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
【输入】
共二行。
第一行是一个整数 n(2≤n≤100),n 表示同学的总数。
第二行有 n 个整数,用空格分隔,第 i 个整数 (130≤
≤230)是第 i 位同学的身高(厘米)。
【输出】
一个整数,最少需要几位同学出列。
样例输入
8
186 186 150 200 160 130 197 220
样例输出
4
解题思路
这个题目不是单纯的递增或者递减数列,而是先递增再递减。
我首先想的是:从1 到 n 存入身高,初始化动态 dp 数组,每个里面的值赋为 i-1(例如第 1 个 dp[1]=0),然后从 2 到 n 进行遍历(代表的是递增的节制点 k),然后分情况讨论:内部进行两个循环,一个循环对 1 至 k 进行考虑,如果不满足 a[j]<a[i],就重新赋值,dp[i]= min(dp[i],dp[j]+1),但是这里要考虑一个问题是:如果去掉了一个人(他的编号是 x),那么他的下一个人(x+1)的身高还是和第 x 个人比较,这里会有些复杂, dp 数组里面更新的最小值,是从哪一个人开始更新的,说明这个人不用考虑,可能还需要用一个值存储更新的这个人的前一个人的身高。这是计算递增情况的,然后递减情况类似。
然后我看了下题解,他们的思路都很像:是先用两层循环,目的是从第 1 个人到第 n 个人找对应下标的最大升序列,再用两层循环从第 n 个人到第 1 个人找对应下标的最大升序列。
题目不就是要找前一部分是升序,后一段是从后往前的升序嘛!那将两个升序对应的下标的值相加,注意要减一,因为前一段和后一段的中间那个数,计算了两次。
然后计算上的人数就是符合要求的,要求的是去除的人数,就用 n-max ,max是统计人数时出现的最大值。
先用代码解决找升序的问题:
for(i=1;i<=n;i++)//从左到右找递增的个数 {for(j=0;j<i;j++){if(a[j]<a[i])b[i]=max(b[i],b[j]+1);} }不过要注意的是:尽管数列是从第 1 个人开始数的,但是内存循环的 j=0 ,全局变量中 a[0]=0,对于第一个人来说,这个人肯定要入列,这时 a[1]>a[0],b[1]=b[0]+1(其实也可以在初始化时就把b[1] 赋值为1,也是一样的效果)。 对于后一段也是同样的思路。
代码如下:
#include<stdio.h>
int a[105];
int b[105],c[105],sum;
int max(int x,int y)
{if(x<y)return y;elsereturn x;
}
int main()
{int n,i,j;scanf("%d",&n);for(i=1;i<=n;i++){scanf("%d",&a[i]);}for(i=1;i<=n;i++)//从左到右找递增的个数 {for(j=0;j<i;j++){if(a[j]<a[i])b[i]=max(b[i],b[j]+1);} }for(i=n;i>0;i--)//从左往右找递减的个数 {for(j=n+1;j>i;j--){if(a[i]>a[j])c[i]=max(c[i],c[j]+1);}}for(i=1;i<=n;i++)sum=max(sum,c[i]+b[i]-1);//找中途出现的最大值 printf("%d",n-sum);return 0;
}相关文章:
洛谷——P1091 合唱队形
【题目描述】 n 位同学站成一排,音乐老师要请其中的 n−k 位同学出列,使得剩下的 k 位同学排成合唱队形。 合唱队形是指这样的一种队形:设 kk 位同学从左到右依次编号为 1,2, … ,k,他们的身高分别为,, … ,,则…...
使用logstash把mysql同步到es,Kibana可视化查看
1:首先需要电脑本地有es环境,并且要牢记版本后,后续安装的logstash和Kibana一定要版本对应 查看es版本:http://localhost:9200/ 2:安装对应版本的logstash:找到自己对应ES版本,然后解压 Logst…...

Vue3.0 setup的使用及作用
目录开篇:1.什么是setup2.setup怎么使用3.setup中包含的生命周期函数3.setup相关参数4.setup特性总结总结开篇: 从vue2升级 vue3,vue3是可以兼容vue2。所以v3可以采用v2的选项式api,但是v2不能使用v3的组合式api,由于…...

Ubuntu18.04安装Vertica
目录下载安装包安装(Ubuntu18.04)配置 I/O Scheduler配置 TZSupport Tools配置 swapinessDisk ReadaheadEnabling chrony or ntpd自启动项错误处理后重装下载安装包 官网11.0版本或者10.0(deb)安装包可私信提供百度网盘链接; 安装(Ubuntu18.04) testvertica:~$ s…...
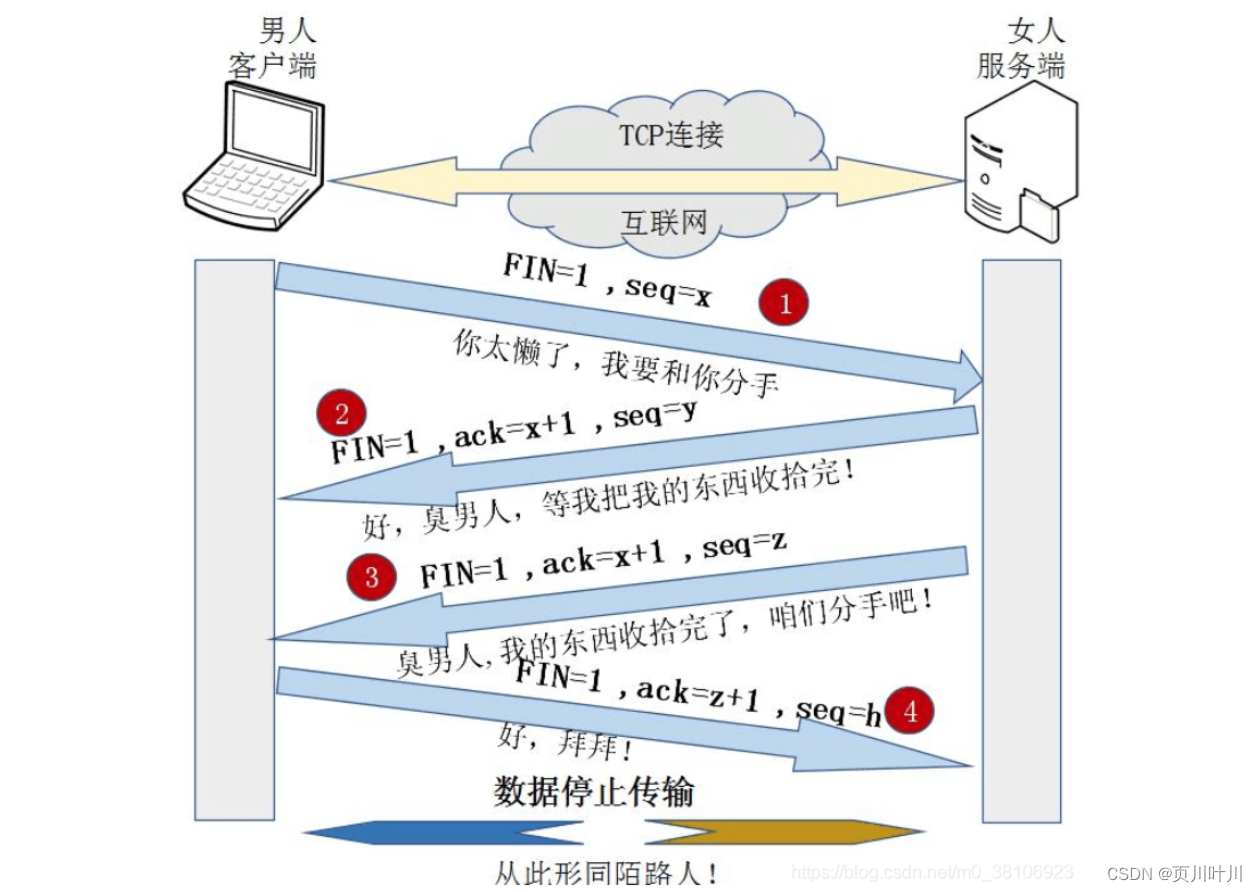
2.计算机基础-计算机网络面试题—基础知识、容器、面向对象、并发编程
本文目录如下:计算机基础-计算机网络 面试题一、基础知识简述 TCP 和 UDP 的区别?http与https的区别?Session 和 Cookie 有什么区别?URL是什么?由哪些部分组成?OSI 的 五层模型 都有哪些?get 和 post 请求…...
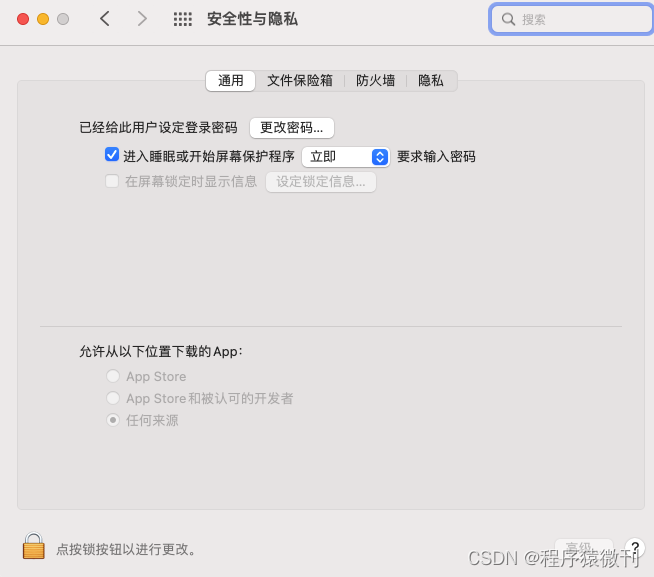
解决Mac 安装应用提示:xx已损坏,无法打开。 您应该将它移到废纸篓问题
许多新手mac 用户安装应用得时候会出现 “已损坏,无法打开。您应该将它移到废纸娄” 导致无法正常安装,其实应用软件b并没有损坏,只是系统安全设置,我们改如何解决呢? 1、开启允许任何来源 苹果已经取消了允许“任何…...

xpath注入[NPUCTF2020]ezlogin
[NPUCTF2020]ezlogin 打开界面 如果发现自己输入的信息由这样构成,可以往xpath注入上靠一下。 不管输入什么,很容易发现登陆就超时了,说明这里token是不断刷新的。 这样构造也是一样的目的都是为了闭合后面的,为啥有两个or呢 us…...

【Python学习笔记】22.Python3 数据结构
前言 本章节我们主要结合前面所学的知识点来介绍Python数据结构。 列表 Python中列表是可变的,这是它区别于字符串和元组的最重要的特点,一句话概括即:列表可以修改,而字符串和元组不能。 以下是 Python 中列表的方法…...
一文搞懂 什么是CPU上下文?为什么要切换?如何减少切换?
最近经常有小伙伴问到的一些问题,比较集中的是关于CPU切换. 实际用C/C,go开发,你会特别注意内存和CPU的使用情况,那些对于CPU使用情况特别关注,或者性能特别关注的朋友可以看看这篇文章,相信看完结尾的示例…...
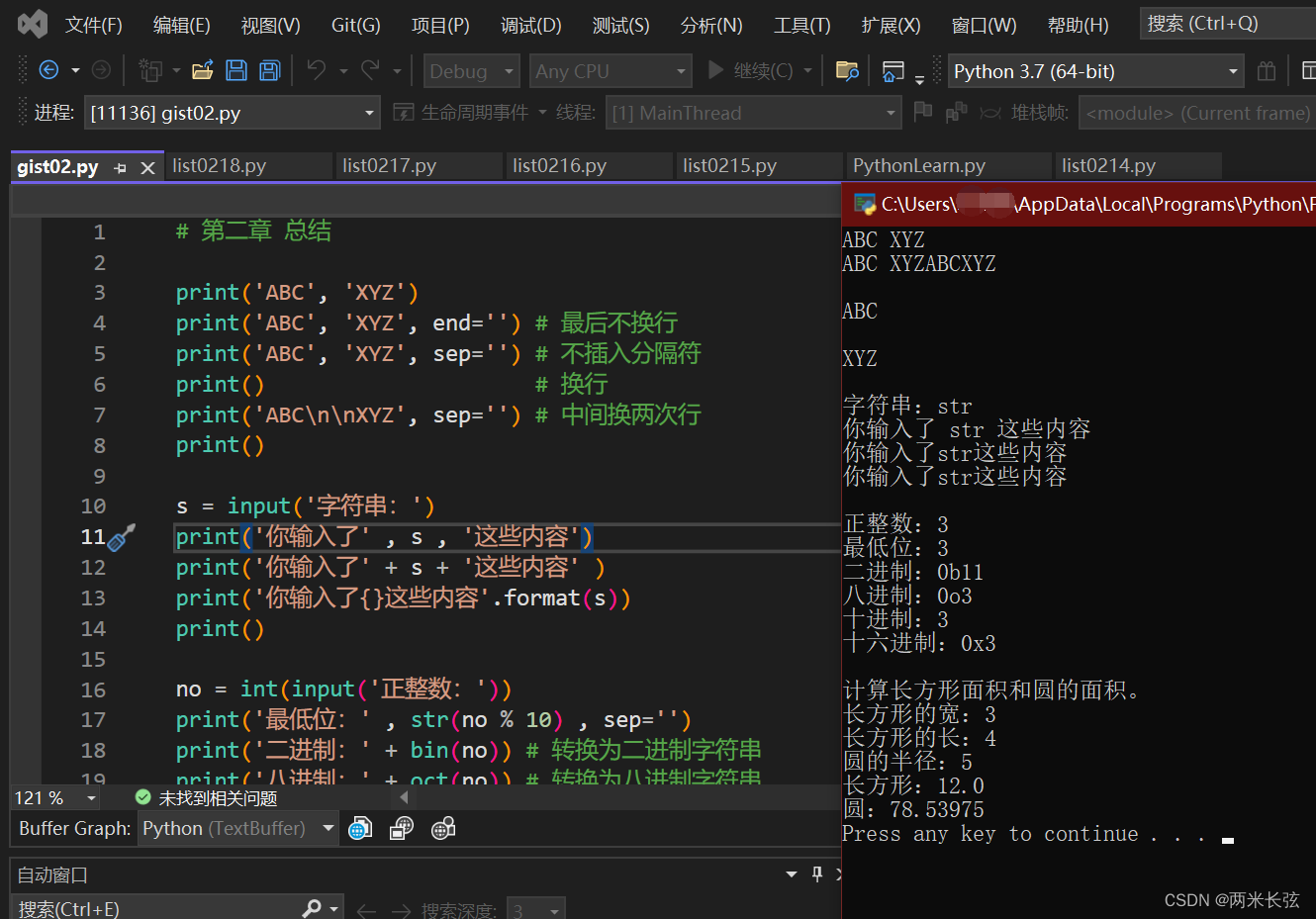
【Python】Python学习笔记(二)基本输入输出
Python娘来源:https://next.rikunabi.com/tech/docs/ct_s03600.jsp?p002412 目录print()函数不进行自动换行的print()函数打印输出多个字符串只进行换行input()函数使用format方法格式化字符串字符串与数值转换字符串转换为数值数值转换为字符串总结参考资料print(…...

LeetCode刷题系列 -- 724. 寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于…...

Linux编辑器vim
本文已收录至《Linux知识与编程》专栏! 作者:ARMCSKGT 演示环境:CentOS 7 目录 前言 正文 vim常用方式 进入vim 退出vim vim基本模式及模式功能 命令模式 插入模式 底行模式 替换模式 视图模式 配置vim 自己配置vim 自动化配置…...

基于“python+”潮汐、风驱动循环、风暴潮等海洋水动力模拟
查看原文>>>基于“python”潮汐、风驱动循环、风暴潮等海洋水动力模拟ADCIRC是新一代海洋水动力计算模型,它采用了非结构三角形网格广义波动连续方程的设计,在提高计算精确度的同时还减小了计算时间。被广泛应用于:模拟潮汐和风驱动…...
《Terraform 101 从入门到实践》 第二章 Providers插件管理
《Terraform 101 从入门到实践》这本小册在南瓜慢说官方网站和GitHub两个地方同步更新,书中的示例代码也是放在GitHub上,方便大家参考查看。 不怕出身低,行行出状元。 插件 Terraform可以对多种平台的多种资源进行管理,这个是通过…...
)
03- pandas 数据库可视化 (机器学习)
pandas库的亮点: 一个快速、高效的DataFrame对象,用于数据操作和综合索引;用于在内存数据结构和不同格式之间读写数据的工具:CSV和文本文件、Microsoft Excel、SQL数据库和快速HDF 5格式;智能数据对齐和丢失数据的综合处理&#…...
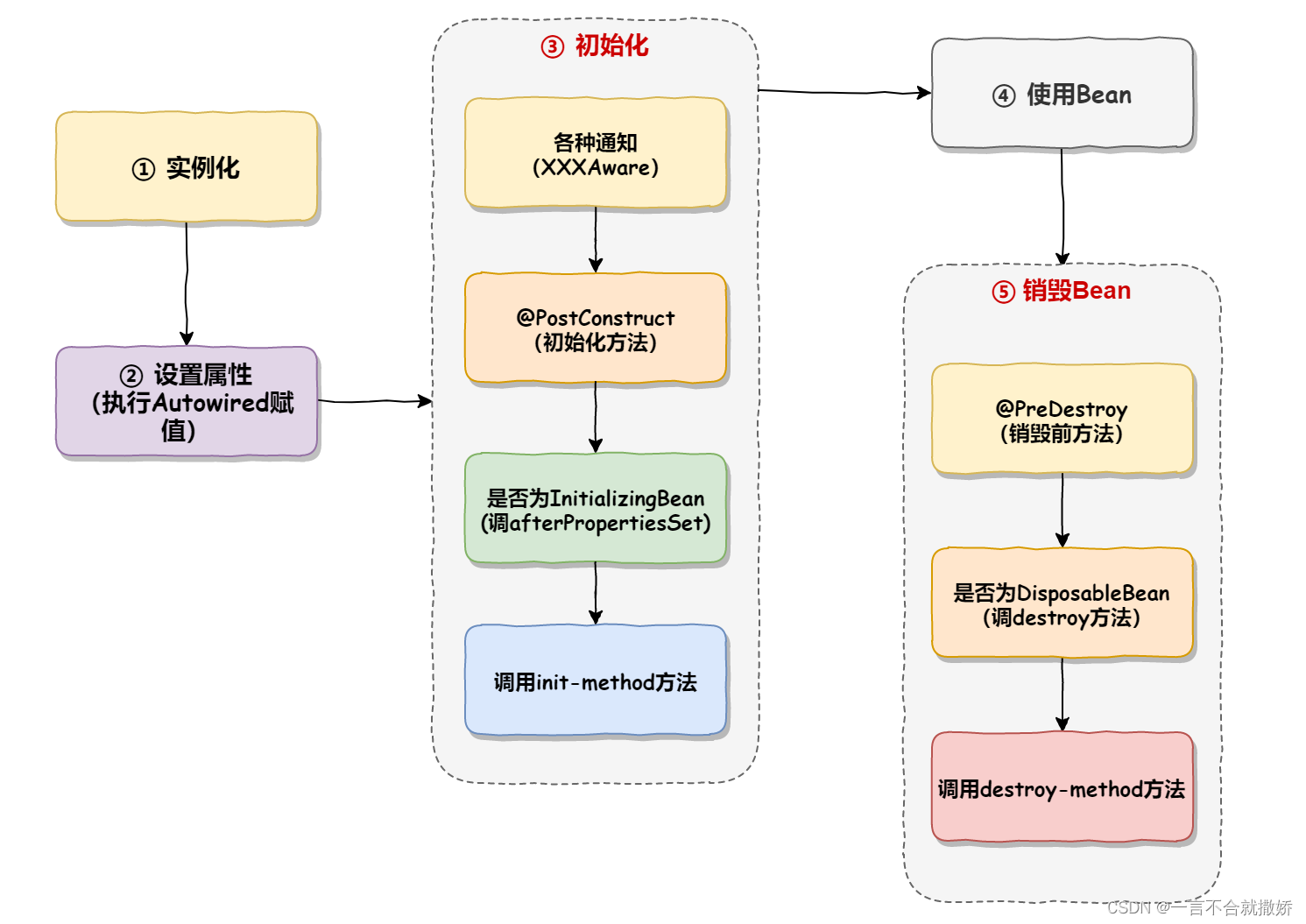
Spring为什么这么火 之 Bean的6种作用域和Bean的生命周期
1、Bean的作用域 1.1、什么是作用域? 限定程序中变量的可用范围叫做作用域,或者说在源代码中定义变量的某个区域就叫做作用域 1.2、Bean的6种作用域 singleton:单例作用域prototype:原型作用域【多例作用域】request࿱…...

【CSS面试题】2023前端最新版css模块,高频15问
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:博主收集的CSS面试题 目录 一、CSS必备面试题 1.CSS3新特性 2.CSS实现元素两个盒子垂…...

SpringCloud-Netflix学习笔记10——Hystrix实现服务熔断
一、概述 1、分布式系统面临的问题 复杂分布式体系结构中的应用程序有数十个依赖关系,每个依赖关系在某些时候将不可避免的失败! 2、服务雪崩 多个微服务之间调用的时候,假设微服务A调用微服务B和微服务C,微服务B 和微服务C又…...
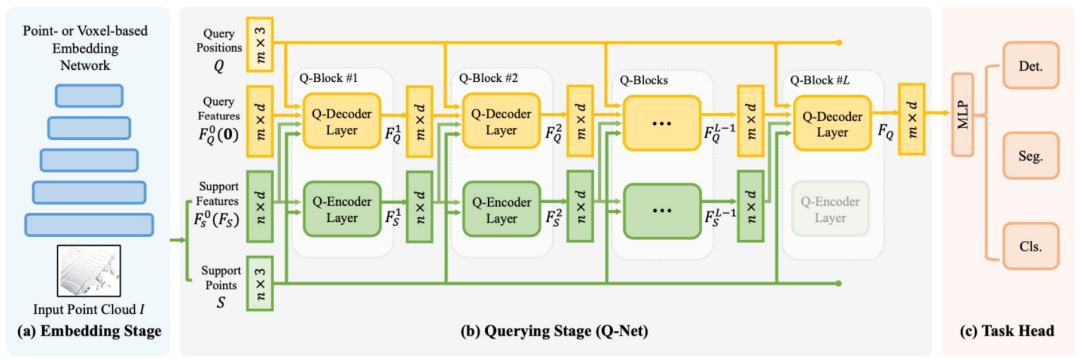
精华文稿|迈向统一的点云三维物体检测框架
分享嘉宾 | 杨泽同 文稿整理 | William 嘉宾介绍 Introduction 3D检测是在三维世界中去定位和分类不同的物体,与传统2D检测的区别在于它有一个深度信息。目前,大部分的工作是倾向于用点云去做三维检测,点云实际上是通过传感器去扫描出来的一…...
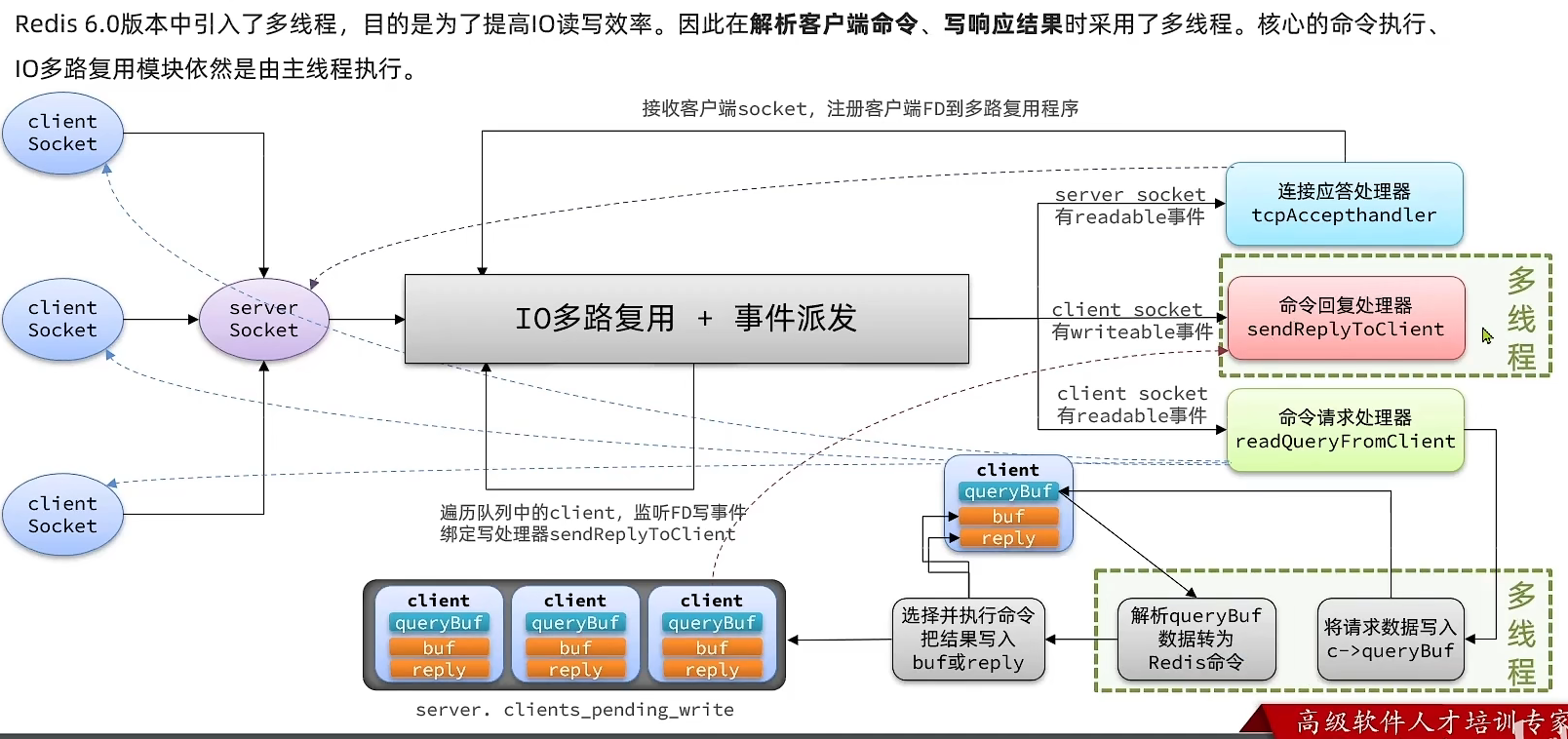
面试题:Redis网络模型
1 用户空间和内核空间以Centos 7 linux操作系统为例。计算机系统被内核操控, 内核被应用操控。为了避免用户应用导致冲突甚至内核崩溃,用户应用与内核是分离的进程的寻址空间会划分为两部分:内核空间、用户空间。用户空间只能执行受限的命令(Rin3&#x…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
