2024秋招BAT核心算法 | 详解图论
图论入门与最短路径算法
图的基本概念
由节点和边组成的集合
图的一些概念:
①有向边(有向图),无向边(无向图),权值
②节点(度),对应无向图,度就是节点连着几条边,对于有向图就是出度加入度
③完全连通图
④子图
⑤路径
⑥完全图,每两节点间都有一条边相连
图的遍历:
①:深度优先搜索
注意:有向图和无向图的遍历不一样
②:广度优先搜索
图的存储:
邻接矩阵
①邻接矩阵->多维数组(二维,n * n,n为节点数);
设两点连通为1
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OAScE9CE-1678185603035)(C:\Users\86166\Desktop\截图\图的存储.png)]](https://img-blog.csdnimg.cn/b7e805a598bd4c88a09e8ac7ad9db873.png)
如果有权值
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2bLCLjsn-1678185603036)(C:\Users\86166\Desktop\截图\图的存储 - 副本.png)]](https://img-blog.csdnimg.cn/34e7ad39537e41f6b547dc6a9d70757e.png)
优点:快速且直观地每两个点间的关系(如果要判断x和y之间的关系,直接通过访问arr[x] [y]或arr[y] [x]获得两点信息)
缺点:存储了一些无用信息,浪费空间;不能快速地访问以某点为起点的所有的边。
代码演示:
#include<iostream>
using namespace std;int n, m, arr[105][105];int main() {cin >> n >> m;//n为节点个数//m为边的个数,每条边带一个权值,一个循环把权值存到数组里面for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;arr[a][b] = c;}//输出for (int i = 1; i<= n; i++) {cout << i << ":";for (int j = 1; j <= n; j++) {if (arr[i][j] != 0) {cout << "{" << i << "->" << arr[i][j] << "}";}}cout << endl;}return 0;
}
Floyd算法
算法解决问题:多源(多个原点)最短路径问题
核心思想:为了取最小值,所以把所有路径初始化为最大,一般为0x3F,然后将各种路径算一遍,取两点最小距离的路径作为此最短路径,因为两个两点路径的其中一个路径可以从另外两个两点路径获得,所以每两点路径都是可以用两点路径获得或者两个两点路径获得
核心思想图示:以1->3 , 1->2->5->4->3为例
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wpvd42AG-1678185603036)(C:\Users\86166\Desktop\截图\图的存储 - 副本 - 副本.png)]](https://img-blog.csdnimg.cn/25b55b83510448a9b796109f54d7e423.png)
核心代码:
memset(arr, 0x3F, sizeof(arr));//初始化(极大值)
for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {for (itn k = 1; k <= n; k++) {arr[j][k] = min(arr[j][k], arr[j][i] + arr[i][k]);//从j到k的最短路,arr[j][i] + arr[i][k]为经过i点中转,从j到i再到k。注意,无论之间有多少个中转点,每三个都会被合并为一个,比如15234,合并523后会变成154}}
}
oj746题:
#include<iostream>
#include<cstring>
using namespace std;
int n, m, s, arr[1005][1005];
int main() {memset(arr, 0x3F, sizeof(arr));//初始化(极大值)cin >> n >> m;for (int i = 0; i < m; i++) {//全边(保留权值最小的边)int a, b, c;cin >> a >> b >> c;if (arr[a][b] > c) {arr[a][b] = c;arr[b][a] = c;}}for (int i = 1; i <= n; i++) {//floydfor (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {arr[j][k] = min(arr[j][k], arr[j][i] + arr[i][k]);//从j到k的最短路,arr[j][i] + arr[i][k]为经过i点中转,从j到i再到k}}}arr[s][s] = 0;for (int i = 1; i <= n; i++) {if (arr[s][i] = 0x3F3F3F3F) {cout << -1 << endl;//还是原本最大值就说明到不了} else {cout << arr[s][i] << endl;}}return 0;}邻接表
邻接表:构建一个列数可变的二维数组,根据节点数定义定义行数
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-x2wrDeYt-1678185603037)(C:\Users\86166\Desktop\截图\邻接表.png)]](https://img-blog.csdnimg.cn/94c8f1cdc35e441798b89ed4b57ec88d.png)
邻接表的优缺点和邻接矩阵的优缺点互补
优点:①、省空间②、快速访问以某点为起点的所有点
缺点:①不能快速判断两点间的关系
代码演示:
基础理解代码:
#include<iostream>
using namespace std;int n, m, num[105][105][2];int main() {cin >> n >> m;for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;//a为起点节点,b为终点节点,c为权值num[a][++num[a][0][0]][0] = b;num[a][num[a][0][0]][1] = c;}for (int i = 1; i <= n; i++) {cout << i << ":";for (int j = 1; j <= num[i][0][0]; j++) {cout << "{" << num[i][j][0] << "," << num[i][j][1] << "}";}cout << endl;}return 0;
}全部代码:
#include<iostream>
#include<vector>
using namespace std;
//保存终点节点和此路径的权值,也可用键值对来保存
struct edge {int e, v;
};int main() {int n, m;cin >> n >> m;//n为节点数,m为边数vector<vector<edge> > edg(n + 1, vector<edge>());for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;edg[a].push_back((edge){b, c});//a为起点节点,b为终点节点,c为权值}for (int i = 1; i <= n; i++) {cout << i << ":" ;for (int j = 0; j <= edg[i].size(); j++) {cout << "{" << i << "->" << edg[i][j].e << "," << edg[i][j].v << "}";}cout << endl;}return 0;
}Dijkstra算法
算法解决问题:解决单源(一个原点)最短路径的问题
算法前提:不能有负权边,负环(在环的路径中路径值无限减小)没有最短路
核心思想:
用一个数组保存一个能到此节点的所有的距离
核心思想图示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JcP0I6Sz-1678185603037)(C:\Users\86166\Desktop\截图\邻接表2.png)]](https://img-blog.csdnimg.cn/b24ab59ba4a34ceb9da656c03333e5aa.png)
代码演示:
#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;//每个点的各种状态,为了优先队列为一个小顶堆,且这个排序根据原点到当前节点的距离,排序的目的是为了编号从小到大去遍历
struct node {int now, dis;//now为当前点,dis为到这的总长度bool operator< (const node &b) const {return this->dis > b.dis;}
};struct edge {int e, v;//e为当前点的编号,v为权值
};//ans[i]数组保存是从原点到编号为i点距离
int n, m, s, ans[100005];int main() {memset(ans, 0x3F, sizeof (ans));cin >> n >> m >> s;//n为节点数,m为边数,s为源点编号vector<vector<edge> > edg(n + 1, vector<edge>());for (int i = 0; i < m; i++) {int a, b, c;//a为起点节点,b为终点节点,c为权值cin >> a >> b >> c;//无向图edg[a].push_back((edge){b, c});edg[b].push_back((edge){a, c});}priority_queue<node> que;//que.push((node){s, 0});//起始元素加入队列, now为s,dis为0ans[s] = 0;//起点答案置为0while (!que.empty()) {node temp = que.top();que.pop();if (temp.dis > ans[temp.now]) {//如果答案已被固定,也就是此时遍历点的 原点到此点的距离 如果大于 当前点的 原点到此点的距离continue;}//遍历以遍历点为起点的每一条边for (int i = 0; i < edg[temp.now].size(); i++) {int e = edg[temp.now][i].e;//temp.now为当前的点的编号,e为当前点到达的终点int v = edg[temp.now][i].v;//v为当前点到达终点的权值if (ans[e] > ans[temp.now] + v) {//ans[temp.now]保存的是从原点到当前点的距离,如果,从原点到当前点的距离和当前点到某终点的权值之和小于从原点到当前点的距离就把这个点放到优先队列,且更新从原点到当前点的距离ans[e] = ans[temp.now] + v;que.push((node){e, ans[e]});}}}for (int i = 1; i <= n; i++) {if (ans[i] == 0x3F3F3F) {cout << -1 << endl;} else {cout << ans[i] <<endl;}}return 0;
}链式前向星
静态链表:用一个数组来存节点,每个数组元素包括数据域和指针域,指针域保存下一个节点的索引
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MaYmraVt-1678185603038)(C:\Users\86166\Desktop\截图\静态链表1.png)]](https://img-blog.csdnimg.cn/4a773e8e0bfc4780b5216becdfe3c95d.png)
链式前向星=>采取头插法的静态链表
意义:保存每两个有联系点
解释:首先需要两个数组,一个数组为head,这个数组的索引为各个起点编号,head[i]保存的是以i为起点的最后一条边(最后一个终点)的编号;另一个数组为静态链表edg,edg[i].next保存的是以i这条边同起点的上一条边的编号,edg[i].edge保存的是终点编号。
保存过程:首先根据一个起始点的编号把终点存到数组中一个空的位置,如以编号为1的起始点:
首先会把3存到edg[1].edge = 3,且把head数组中存的最后一个终点的索引放到其指针域,edge[1].next = head[1],然后在head数组里面保存到目前为止起始点1的最后一条边指向的终点在edg数组的索引,head[1] = 1;
然后就把编号2存到edge[2].edge = 2,然后一样edge[2].next = head[1],更新最后一条边的终点的下标,head[1] = 2
依此类推…(存一条边有三步:存编号->换索引,存编号edge->留索引next->更新索引head)
存一条边代码:
//a为起点编号,b为终点编号,i为数组中某个空的位置的索引
edg[i].edge = b;
edg[i].next = head[a];
head[a] = i
访问过程:因为head数组索引为起点编号,通过head数组索引开始访问。比如访问起点编号为5
就会访问head[5] 得到一个值5,然后根据5这个这个值作为一个索引访问edg数组edg[5].edge,得到一个值4,所以5->4,然后再根据edg[5].next 得到一个索引4,然后根据这个索引访问edg[4].edge得到一个值2,所以5->2,然后再根据edg[4].next得到一个-1,如果是-1,说明已经是最后一个了。
依此类推…(访问都是从head[i]开始,根据edg[i].next得到下一条边的终点)
图示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ufSwOp2s-1678185603038)(C:\Users\86166\Desktop\截图\链式前向星.png)]](https://img-blog.csdnimg.cn/d9fc389a76bd4434807af31f67ca6f30.png)
代码演示:
#include<iostream>
#include<cstring>
using namespace std;struct node {int e, v, next;
};int n, m, head[105];
node edg[105];int main() {memset(head, -1, sizeof(head));cin >> n >> m;//n为节点数,m为边数for (int i = 0; i < m; i++) {int a, b, c;//a为起点编号,b为终点编号,c为边的权值cin >> a >> b >> c;edg[i].e = b;//任意选一个空的数组索引把终点编号存进去edg[i].next = head[a];//把上一个最后的终点编号保存到指针域edg[i].v = c;//存权值head[a] = i;//保存最后一个的终点在edg数组中的索引}for (int i = 1; i <= n; i++) {cout << i << ":";for (int j = head[i]; j != -1; j = edg[j].next) {cout << "{" << i << "->" << edg[j].e << "," << edg[j].v << "}";}cout << endl;}return 0;
}前向星Dijkstra算法:
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;struct node {int now, dis;//now为搜索到当前节点的编号,dis是从原点到此节点的距离bool operator< (const node &b) const {return this->dis > b.dis;}
};struct edge {int e, v, next;//e为终点编号,v为权值,next为下一个终点的索引
};int n, m, s, ans[200005], head[200005];//n为节点数,m为边数,s为起点编号,ans[i]为i编号节点的最短距离
edge edg[200005];
int cnt_edge;void add_edge(int a, int b, int c) {edg[cnt_edge].e = b;edg[cnt_edge].v = c;edg[cnt_edge].next = head[a];head[a] = cnt_edge++;
}int main() {memset(head, -1, sizeof(head));memset(ans, 0x3F, sizeof(ans));cin >> n >> m >> s;for (int i = 0; i < m; i++) {int a, b, c;//a为起点,b为终点,c为权值cin >> a >> b >> c;add_edge(a, b, c);add_edge(b, a, c);}priority_queue<node> que;que.push((node) {s, 0});ans[s] = 0;while (!que.empty()) {node temp = que.top();que.pop();if (ans[temp.now] < temp.dis) {continue;}for (int i = head[temp.now]; i != -1; i = edg[i].next) {//遍历以temp.now为前驱节点的所有后继节点int e = edg[i].e, v = edg[i].v;if (ans[e] > temp.dis + v) {ans[e] = temp.dis + v;que.push((node) {e, ans[e]});}}}for (int i = 1; i <= n; i++) {if (ans[i] == 0x3F3F3F3F) {cout << -1 << endl;} else {cout << ans[i] << endl;}}return 0;
}bellman-ford算法
目的:解决单源最短路径问题,特殊是可以解决负数权值
bellman-ford算法:暴力,试每一种可能
核心思想:设s为原点到某节点的距离,初始化所有节点的s值为最大值,然后遍历n(n为节点数)遍的m(m为边数)遍,也就是以每个节点为起始点去进行搜索,每一个节点都要搜索m遍。
代码演示:
#include<iostream>
#include<cstring>
using namespace std;struct edge {int s, e, v;
};edge edg[200005];
int n, m, s, edg_cnt, ans[100005];void add_edg(int a, int b, int c) {edg[edg_cnt].s = a;edg[edg_cnt].e = b;edg[edg_cnt++].v = c;
}int main() {memset(ans, 0x3F,sizeof(ans));cin >> n >> m >> s;for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;add_edg(a, b, c);add_edg(b, a, c);}ans[s] = 0;for (int i = 1; i <= n; i++) {for (int j = 0; j < edg_cnt; j++) {int s = edg[j].s, e = edg[j].e, v = edg[j].v;ans[e] = min(ans[e], ans[s] + v);//取终点编号到原点的距离和当前编号到原点距离加上这条边的权值之和中最小的}}for (int i = 1; i <= n; i++) {if (ans[i] == 0x3F3F3F3F) {cout << -1 << endl;} else {cout << ans[i] << endl;}}return 0;
}基于队列优化的Ballmen-ford算法(spfa)
由于原本的Ballmen-ford算法中的一些遍历是多余的,比如如果没有遍历靠经原点的边就去遍历靠后的边,这样的遍历是多余的,因为也不会更新。所以引入了队列,先遍历靠前的再遍历靠后的。
前提:需要一个队列、设置一个ans数组存放最短路径,一个mark标记数组,标记数组标记的是队列中是否存在这个节点编号,入队编号i时就标记mark[i]为1,出队就标记为0;而且要以某种形式存放每个起始节点的终点节点编号,可以是静态链表,也可以是邻接表,下面代码以静态链表为例,所以要构造静态链表就要设置head数组和edg数组,head数组存放某起始节点的最后一条终点编号的所在edg数的索引。
过程:首先是要有个原点,在对队列操作前先把原点插入队列,然后就可以进行队列操作了。把队首元素弹出,以这个弹出的元素为一个起始编号对其所有的终点做个判断,首先判断起始节点编号对应的最短路径数组ans的值加上该起始点到终点的权值和是否小于终点编号对应最短路径数组ans中的值,如果小于说明这个路径更短,就更新终点编号对应ans中的值;再者,就根据标记数组判断队列中是否有这个终点编号,如果没有就入队。一直操作直到队列中没有元素。
图解:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ovghnegt-1678185603038)(C:\Users\86166\Desktop\截图\ballom-ford.png)]](https://img-blog.csdnimg.cn/f953fcb89eaa4b559b6873e58b00ce08.png)
代码演示:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;struct edge {int e, v, next;
};edge edg[200005];
int n, m, s,cnt_edg, ans[100005], head[100005], mark[100005];void add_edg(int a, int b, int c) {edg[cnt_edg].e = b;edg[cnt_edg].v = c;edg[cnt_edg].next = head[a];head[a] = cnt_edg++;
}int main() {memset(ans, 0x3F, sizeof(ans));memset(head, -1, sizeof(head));cin >> n >> m >> s;for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;add_edg(a, b, c);add_edg(b, a, c);}queue<int> que;que.push(s);ans[s] = 0;while (!que.empty()) {int temp = que.front();que.pop();mark[temp] = 0;for (int i = head[temp]; i != -1; i = edg[i].next) {int e = edg[i].e, v = edg[i].v;if (ans[e] > ans[temp] + v) {ans[e] = ans[temp] + v;if (mark[e] == 0) {mark[e] = 1;que.push(e);}}}}for (int i = 1; i <= n; i++) {if (ans[i] == 0x3F3F3F3F) {cout << - 1 << endl;} else {cout << ans[i] << endl;}}return 0;
}图与最短路径总结
图的存储:邻接矩阵O(n*n)、邻接表O(m)、链式前向星(m)
最短路径:floyd(邻接矩阵)(多源)digkstra(邻接表,链式前向星)()(多源)Ballman-ford(邻接表,链式前向星)(单源)spfa(邻接表,链式前向星)(单源,负权变)
图论-最小生成树
图的最小代价生成树
概念:n个节点就选n-1条边,最小生成树不一定,不一定唯一,不一定不唯一,最小生成树代价唯一
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HjEdCSni-1678185603039)(C:\Users\86166\Desktop\截图\最小生成树.png)]](https://img-blog.csdnimg.cn/c8fb8fba7cd34853a2c04db6fb2920f3.png)
Kruskal算法
以边求解
意义:求解最小生成树
过程:对所有边权值排序,选出n-1条权值最小边,从边权值小的遍历到大的,判断两节点是否相连,如果相连就不选中,否则就是。
图示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rd2yVKGp-1678185603039)(C:\Users\86166\Desktop\截图\最小生成树2.png)]](https://img-blog.csdnimg.cn/5388335daf664491be7f90cfa96db5ad.png)
代码演示:
#include<iostream>
#include<algorithm>
using namespace std;struct edge {//s为起始点,e为终点,v为权值,而且重载小于号为了排序按权值的大小排序int s, e, v;bool operator< (const edge &b) const {return this->v < b.v;}
};int n, m, ans, cnt, my_union[100005];//n为节点数,m为边数,my_union数组为并查集,ans为最小代价,cnt为边数
edge edg[100005];//邻接表存图
//初始化并查集,初始每个节点间都不相连,为了后面找到树的边
void init() {for (int i = 1; i <= n; i++) {my_union[i] = i;}
}//并查集的遍历,所有节点的编号就是并查集的下标
int find_fa(int x) {//传进一个起始点编号作为下标,如果该下索引对应的值就是该索引,说明该索引是该树干的最后一个节点if (my_union[x] == x) {return x;}//如果不是就顺着下标找,因为在连接的时候起始点会存有该起始点连接的一个终点编号对应的值return my_union[x] = find_fa(my_union[x]);
}int main() {cin >> n >> m;for (int i = 0; i< m; i++) {cin >> edg[i].s >> edg[i].e >> edg[i].v;}//初始化并查集init();//排序sort(edg, edg + m);for (int i = 0; i < m; i++) {//分别根据权值的小到大在并查集中找起始点和终点是否连接int fa = find_fa(edg[i].s), fb = find_fa(edg[i].e);if (fa != fb) {//如果两点不连接,就连接my_union[fa] = fb;ans += edg[i].v;//加上代价cnt++;//树边数加一if (cnt = n - 1) {//如果树的边树够了说明已经生成最小树,就输出返回cout << ans << endl;return 0;}}}cout << -1 << endl;return 0;
}代码图解:包括小到大并查集操作和递归操作解释
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FQh9opl4-1678185603039)(C:\Users\86166\Desktop\截图\kruskal.png)]](https://img-blog.csdnimg.cn/490f0bc80f98457bafe1aa7e22ee2e18.png)
Prim算法
以点求解最小生成树
意义:求解最小生成树
过程:以某个点为源点,向外扩散,每次选一条权值最小的边
图示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FE8kil3O-1678185603040)(C:\Users\86166\Desktop\截图\krukcal2.png)]](https://img-blog.csdnimg.cn/cb0fd7aeb8244737a3f66fc8210166cc.png)
代码演示:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;//e为终点,v为权值,并且为了后面的堆排序所以重载小于号
struct node {int e, v;bool operator< (const node &b) const {return this->v > b.v;}
};//为后面链式前向星准备
struct edge {int e, v, next;
};edge edg[200005];
int n, m, edg_cnt, ans, mark[100005], cnt, head[100005];//链式前向星存图
void add_edg(int a, int b, int c) {edg[edg_cnt].e = b;edg[edg_cnt].v = c;edg[edg_cnt].next = head[a];head[a] = edg_cnt++;
}int main() {memset(head, -1, sizeof(head));cin >> n >> m;for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;add_edg(a, b, c);add_edg(b, a, c);}priority_queue<node> que;que.push((node){(n / 4 == 0 ? 1 : n / 4), 0});while (!que.empty()) {node temp = que.top();que.pop();//如果弹出的节点的终点已经连接就不再进行判断连接,总结continueif (mark[temp.e] == 1) {continue;} //如果没有连接,就把该节点标记为1,意为连接mark[temp.e] = 1;//代价加上权值ans += temp.v;//边数加一cnt++;//如果已经形成树就返回if (cnt == n - 1) {cout << ans << endl;return 0;}//对一个节点的所以终点进行操作,没有连接就把该终点放到队列中for (int i = head[temp.e]; i != -1; i = edg[i].next) {int e = edg[i].e, v= edg[i].v;if (mark[e] == 0) {que.push((node) {e, v});}}}cout << -1 << endl;return 0;
}图论-拓扑排序
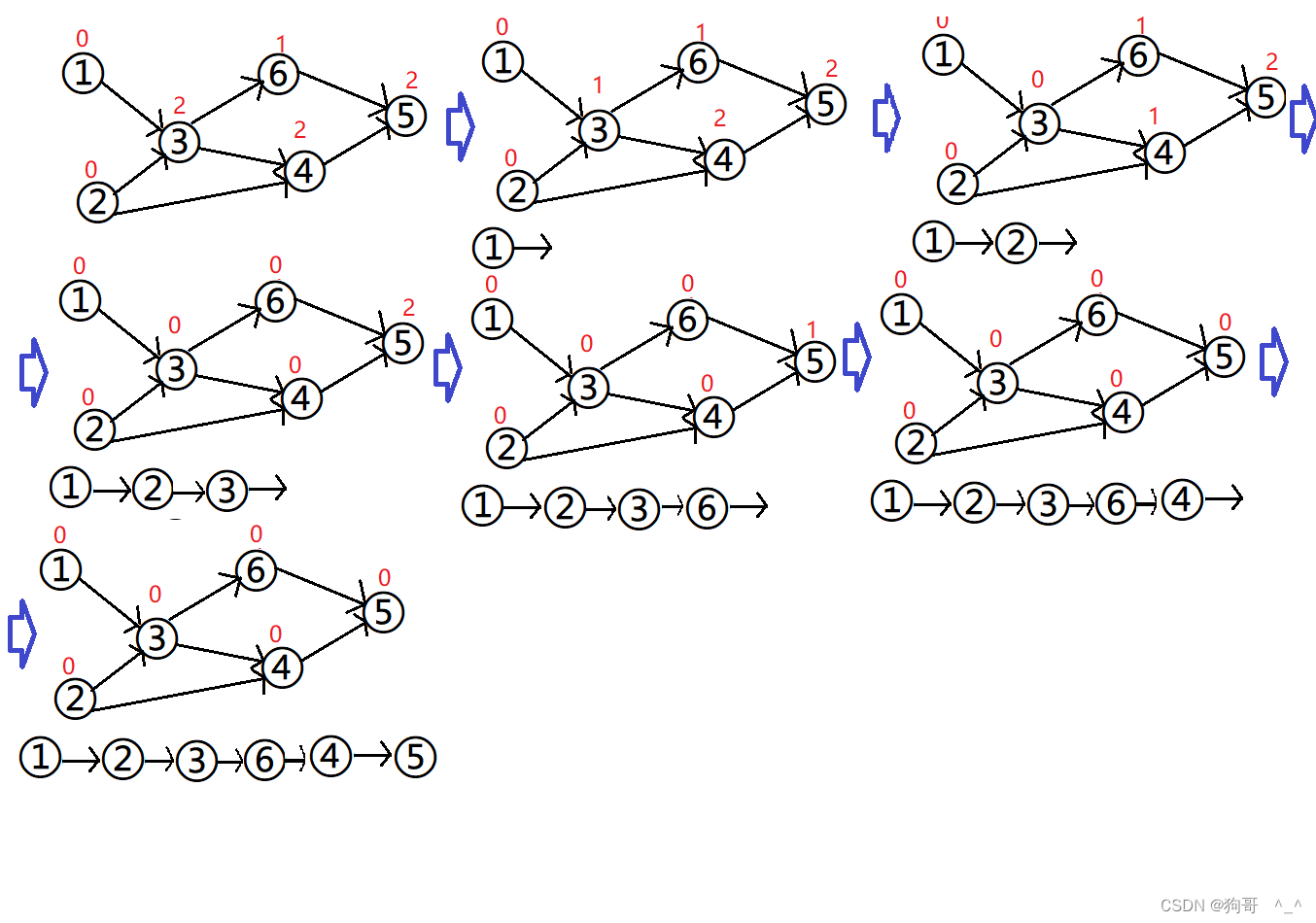
拓扑排序求解:1、找入度为0的节点 2、找到该点后,删除所有以其为起点的边,删除其实就是入度减一。
性质:拓扑排序不唯一,因为可能同时有多个入度为0的点。
应用:判断图是否带环
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Mw5IN7AO-1678185603040)(C:\Users\86166\Desktop\截图\拓扑排序.png)]](https://img-blog.csdnimg.cn/3f323b29c4b94ccfa4e5af595a86a0b4.png)
代码演示:
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;//用于链式前向星存图
struct edge {int e, next;
};edge edg[1005];
//num数组保存答案,in_degree数组统计入度
int n, m, head[105], num[105], cnt, in_degree[105];int main() {memset(head, -1, sizeof(head));cin >> n >> m;for (int i = 0; i < m; i++) {int a, b;cin >> a >> b;in_degree[b]++;//计数入度edg[i].e = b;edg[i].next = head[a];head[a] = i;}//queue<int> que;priority_queue<int, vector<int>, greater<int>> que;//因为拓扑排序有多个结果,所以为了从小到大就用一个小顶堆//队列que保存所有入度为0的元素for (int i = 1; i <= n; i++) {if (in_degree[i] == 0) {que.push(i);}}while (!que.empty()) {int temp = que.top();que.pop();//计数存答案num[cnt++] = temp;//对每个终点的入度减一,如果该入度为0就入队,否则就不需要入队for (int i = head[temp]; i != -1; i = edg[i].next) {int e = edg[i].e;in_degree[e]--;if (in_degree[e] == 0) {que.push(e);}}}//如果是环就输出no,因为有环就不能把所有的节点都入队一遍,所以肯定小于节点数if (cnt != n ) {cout << "no" << endl;return 0;}//否则输出这个顺序for (int i = 0; i < cnt; i++) {i && cout << " ";cout << num[i] << " ";}cout << endl;return 0;}输出所有拓扑排序:
#include<iostream>
#include<vector>
using namespace std;int n, m, f, num[105], in_degree[105], mark[105];void func(int now, vector<vector<int> > &edg) {if (now == n + 1) {//当递归到最后一个节点就输出for (int i = 1; i <= n; i++) {cout << num[i] << " ";}cout << endl;f = 1;return ;}for (int i = 1; i <= n; i++) {//遍历每个节点编号if (in_degree[i] == 0 && mark[i] == 0) {//入度为0且没有遍历过就进行遍历num[now] = i;mark[i] = 1; for (int j = 0; j < edg[i].size(); j++) {//把当前起点的所有的终点的入度减一in_degree[edg[i][j]]--;}func(now + 1, edg);//在递归过程会不断地对入度减一直到最后一个节点遍历完。比如最后一层输出完毕后就会执行以下代码,把标记还原,把入度还原,这就是搜索回溯,回到前一个度数多的一个节点mark[i] = 0;for (int j = 0; j < edg[i].size(); j++) {in_degree[edg[i][j]]++;}}}
}int main() {cin >> n >> m;vector<vector<int> > edg(n + 1, vector<int>());for (int i = 0; i < m; i++) {int a, b;cin >> a >> b;in_degree[b]++;edg[a].push_back(b);}func(1, edg);if (f == 0) {cout << "no" << endl;}return 0;
}相关文章:
2024秋招BAT核心算法 | 详解图论
图论入门与最短路径算法 图的基本概念 由节点和边组成的集合 图的一些概念: ①有向边(有向图),无向边(无向图),权值 ②节点(度),对应无向图,…...

凝聚共识,锚定未来 | 第四届OpenI/O 启智开发者大会NLP大模型论坛成功举办!
2023年2月24日下午,第四届OpenI/O启智开发者大会NLP大模型分论坛在深圳人才研修院隆重举办。该论坛以“开源集智创新探索中文NLP大模型生态发展”为主题,众多业内人士和研发者在此共享NLP领域的前沿动态和研发经验,畅想中国NLP领域的发展前景…...
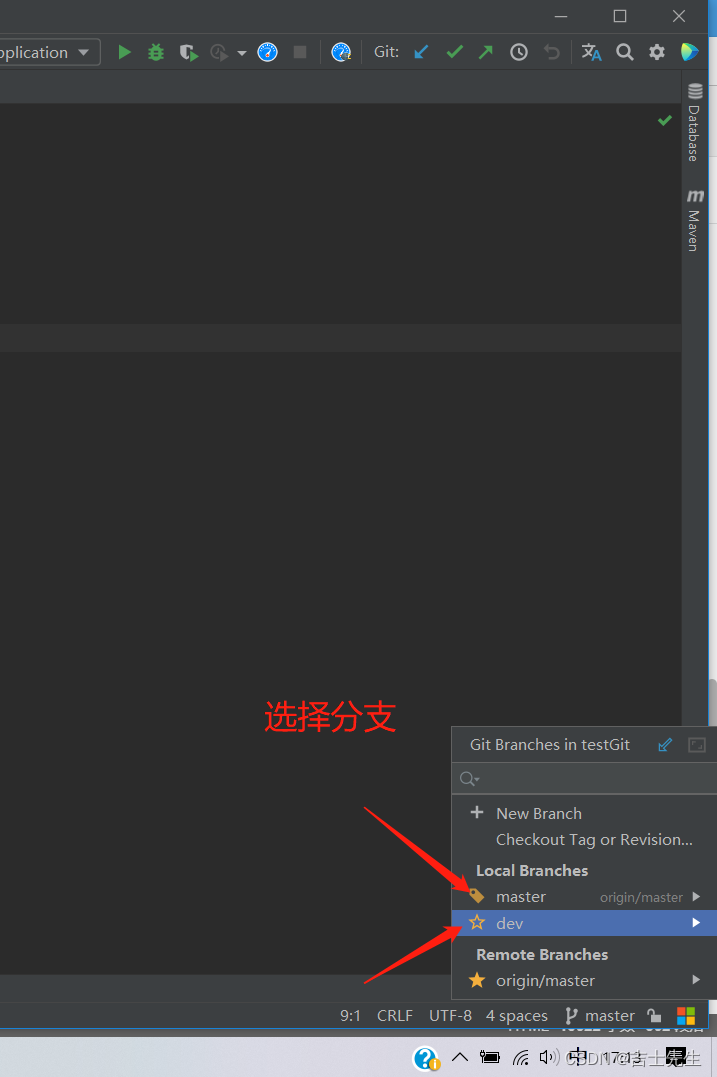
99.【Git】
Git(一)、什么是版本控制1.什么是版本控制2、常见的版本控制工具(二)、版本控制分类1、本地版本控制2、集中版本控制 SVN3、分布式版本控制 Git(三)、Git与SVN的主要区别1、Git历史(四)、Git下载与环境配置1.git下载2、启动Git(五)、常用的Linux命令1.Linux常用命令(六)、Git必…...
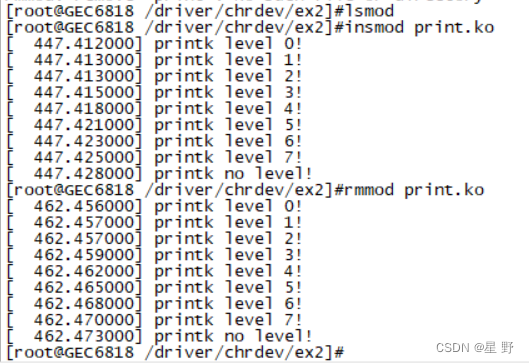
Linux驱动交叉编译把驱动文件放入开发板,以及printk函数打印级别
上一篇介绍了一个最简单的驱动程序和驱动程序大体结构,但那还是用本地编译只能在Ubuntu上运行,我们该怎么编译一个能加载到开发板上呢,就需要交叉编译,交叉编译通常都是在嵌入式开发中使用到的。 交叉编译 理解交叉编译前先了解…...
433. 最小基因变化(2023.03.07))
力扣(LeetCode)433. 最小基因变化(2023.03.07)
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 ‘A’、‘C’、‘G’ 和 ‘T’ 之一。 假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。 例如,“AACCGGTT”…...
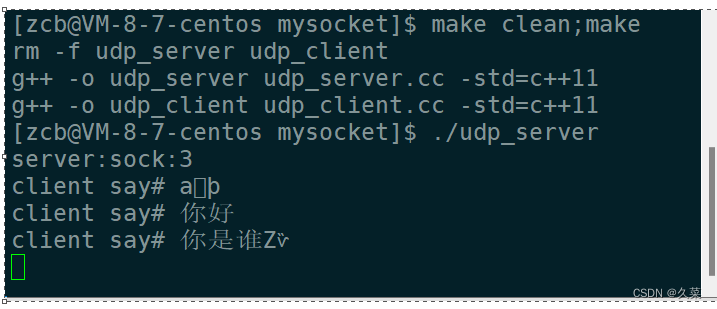
网络基础(2)
目录1. 端口号2. 套接字socket3. 网络通信3.1 sockaddr与sockaddr_in3.2 接口服务端3.2.1 创建套接字,打开网络文件3.2.2 给该服务器绑定端口和ip(特殊处理)3.2.3 初始化相关服务器3.2.4 提供服务客户端3.2.5 绑定3.2.6 使用服务4. makefile实…...

掌握Spring Cloud Gateway:构建高性能API网关的原理和实践
Spring Cloud Gateway 是一个基于 Spring Boot 的 API 网关,用于构建微服务架构中的网关服务。它提供了统一的路由、请求转发、过滤器、负载均衡、熔断等功能,帮助开发者更好地管理和控制微服务系统的请求流量。 本文将介绍 Spring Cloud Gateway 的原理…...
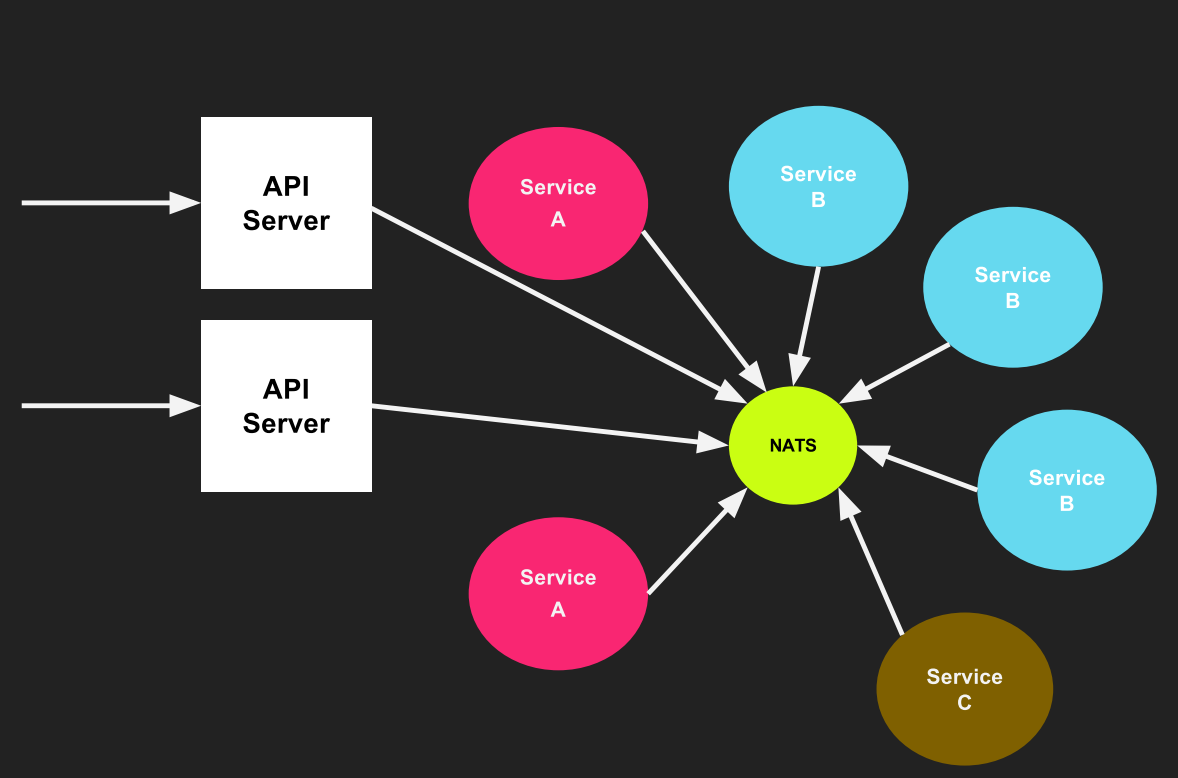
NAST概述
一、NATS介绍 NATS是由CloudFoundry的架构师Derek开发的一个开源的、轻量级、高性能的,支持发布、订阅机制的分布式消息队列系统。它的核心基于EventMachine开发,代码量不多,可以下载下来慢慢研究。 不同于Java社区的kafka,nats…...

【JS知识点】——原型和原型链
文章目录原型和原型链构造函数原型显式原型(prototype)隐式原型(\_\_proto\_\_)原型链总结原型和原型链 在js中,原型和原型链是一个非常重要的知识点,只有理解原型和原型链,才能深刻理解JS。在…...
c盘怎么清理到最干净?有什么好的清理方法
c盘怎么清理到最干净?有什么好的清理方法?清理C盘空间是电脑维护的重要步骤之一。C盘是Windows操作系统的核心部分,保存了许多重要的系统文件,因此空间不足会影响计算机的性能和稳定性。下面是一些清理C盘空间的方法 一.清理临时文件 在使用…...
day26_HTML
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、二阶段介绍 二、HTML 零、 复习昨日 见代码 一、二阶段介绍 第一阶段: 基础入门 java基本语法编程基础(方法,数组)面向对象编程常用类高级(IO,线程,新…...

深度剖析C语言预处理
致前行的人: 人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定冷静,学习如何从慌乱中找到生机。 目录 1.程序翻译过程: 2.字符串宏常量 3.用宏定义充当注释符号 4…...
【WPF 值转换器】ValueConverter 进阶用法
【WPF 值转换器】ValueConverter 进阶用法介绍基类实现子类实现效果介绍 值转换器在WPF开发中是非常常见的,当然不仅仅是在WPF开发中。值转换器可以帮助我们很轻松地实现,界面数据展示的问题,如:模块隐藏显示、编码数据展示为可读…...
Vue2的基本使用
一、vue的基本使用 第一步 引入vue.js文件 <script src"https://cdn.staticfile.org/vue/2.7.0/vue.min.js"></script> 或者<script src"./js/vue.js"></script> 第二步 在body中设置一个挂载点 {{msg}} <div id"app…...

【云原生kubernetes】k8s数据存储之Volume使用详解
目录 一、什么是Volume 二、k8s中的Volume 三、k8s中常见的Volume类型 四、Volume 之 EmptyDir 4.1 EmptyDir 特点 4.2 EmptyDir 实现文件共享 4.2.1 关于busybox 4.3 操作步骤 4.3.1 创建配置模板文件yaml 4.3.2 创建Pod 4.3.3 访问nginx使其产生访问日志 4.3.4 …...
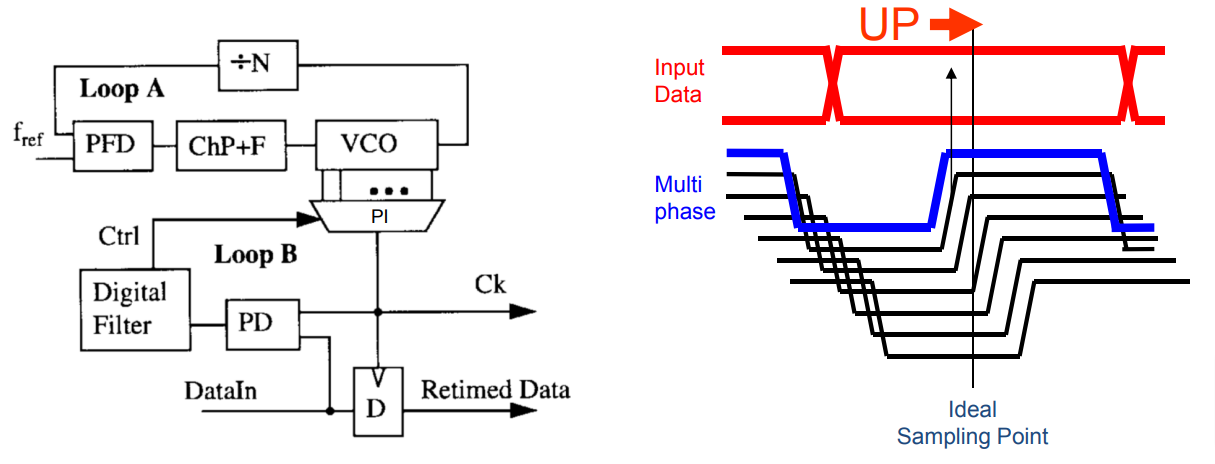
SerDes---CDR技术
1、为什么需要CDR 时钟数据恢复主要完成两个工作,一个是时钟恢复,一个是数据重定时,也就是数据的恢复。时钟恢复主要是从接收到的 NRZ(非归零码)码中将嵌入在数据中的时钟信息提取出来。 2、CDR种类 PLL-Based CDROve…...

如何实现在on ethernetPacket中自动回复NDP response消息
对于IPv4协议来说,如果主机想通过目标ipv4地址发送以太网数据帧给目的主机,需要在数据链路层填充目的mac地址。根据目标ipv4地址查找目标mac地址,这是ARP协议的工作原理 对于IPv6协议来说,根据目标ipv6地址查找目标mac地址,它使用的不是ARP协议,而是邻居发现NDP(Neighb…...
CSS清楚浮动
先看看关于浮动的一些性质 浮动使元素脱离文档流 浮动元素可以设置宽高,在CSS中,任何元素都可以浮动,浮动元素会生成一个块级框,而不论其本身是何种元素。 如果没有给浮动元素指定高度,,那么它会以内容的…...
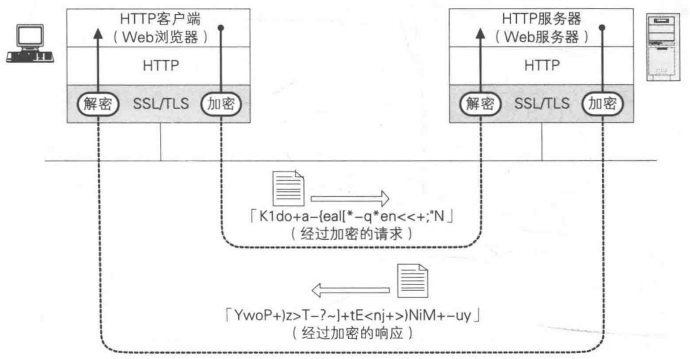
HTTPS详解(原理、中间人攻击、CA流程)
摘要我们访问浏览器也经常可以看到https开头的网址,那么什么是https,什么是ca证书,认证流程怎样?这里一一介绍。原理https就是httpssl,即用http协议传输数据,数据用ssl/tls协议加密解密。具体流程如下图&am…...
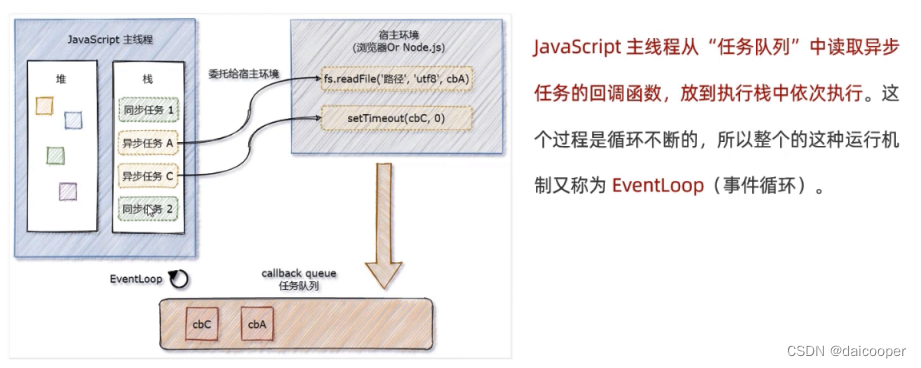
EventLoop机制
JavaScript 是单线程的语言 JavaScript 是一门单线程执行的编程语言。也就是说,同一时间只能做一件事情。 单线程执行任务队列的问题: 如果前一个任务非常耗时,则后续的任务就不得不一直等待,从而导致程序假死的问题。 同步任…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
