01串的熵(蓝桥杯)
文章目录
- 01串的熵
- 问题描述
- 答案:11027421
- 题意解释
- 暴力枚举
01串的熵
问题描述
对于一个长度为n的01串 S= x 1 x 2 x 3 x_{1}x_{2}x_{3} x1x2x3… x n x_{n} xn,香农信息熵的定义为 H(S) = − ∑ 1 n p ( x i ) l o g 2 ( p ( x i ) ) -\sum _{1}^{n}p(x_{i})log_{2}(p(x_{i})) −∑1np(xi)log2(p(xi)),其中 p(0), p(1) 表示在这个01串中0和1出现的占比。
比如,对于 S=100 来说,信息熵 H(S) = − 1 3 l o g 2 ( 1 3 ) − 2 3 l o g 2 ( 2 3 ) − 2 3 l o g 2 ( 2 3 ) -\frac{1}{3}log_{2}(\frac{1}{3})-\frac{2}{3}log_{2}(\frac{2}{3})-\frac{2}{3}log_{2}(\frac{2}{3}) −31log2(31)−32log2(32)−32log2(32) = 1.3083
对于一个长度为23333333的01串,如果其信息熵为11625907.5798,且0出现次数比1少,那么这个01串中0出现了多少次?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填与这个整数,填与多余的内容将无法得分。
答案:11027421
题意解释
这道题目是关于香农信息熵的计算问题。香农信息熵是信息论中用来量化信息预期值的一个概念,通常用于衡量信息的不确定性。在这个问题中,我们需要根据给定的信息熵值和一些条件来计算一个长度为23333333的01串中0出现的次数。
题目描述了一个长度为n的二进制字符串S,由0和1组成。香农信息熵H(S)的计算公式为:
H(S) = − ∑ 1 n p ( x i ) l o g 2 ( p ( x i ) ) -\sum _{1}^{n}p(x_{i})log_{2}(p(x_{i})) −∑1np(xi)log2(p(xi))
其中, p(xi) 表示在字符串中字符i出现的相对频率。对于二进制字符串,i只能是0或1,所以上式中的求和是对i=0和i=1的情况。
题目给出了一个具体的例子,对于字符串S=100,其信息熵计算如下:
H ( S ) = − p ( 0 ) log 2 ( p ( 0 ) ) − p ( 0 ) log 2 ( p ( 0 ) ) − p ( 1 ) log 2 ( p ( 1 ) ) H(S) = -p(0) \log_2(p(0)) -p(0) \log_2(p(0))- p(1) \log_2(p(1)) H(S)=−p(0)log2(p(0))−p(0)log2(p(0))−p(1)log2(p(1))
由于字符串S=100中,0出现了两次,1出现了一次,所以p(0)=2/3,p(1)=1/3,代入公式得到:
H ( S ) = − 2 3 log 2 ( 2 3 ) − 2 3 log 2 ( 2 3 ) − 1 3 log 2 ( 1 3 ) H(S) = -\frac{2}{3} \log_2\left(\frac{2}{3}\right) -\frac{2}{3} \log_2\left(\frac{2}{3}\right)- \frac{1}{3} \log_2\left(\frac{1}{3}\right) H(S)=−32log2(32)−32log2(32)−31log2(31)
现在,我们有一个长度为23333333的01串,其信息熵已知为11625907.5798。题目还告诉我们,这个字符串中0出现的次数比1少。我们的任务是计算出0出现的次数。
为了解决这个问题,我们需要设置两个变量,分别表示0和1出现的次数,然后根据信息熵的定义和给定的条件建立方程,求解这个方程即可得到0出现的次数。需要注意的是,由于0出现的次数比1少,我们可以设0的次数为x,1的次数为23333333-x。
暴力枚举
这段代码是用C++编写的,目的是计算在一个给定长度和信息熵的01串中0出现的次数。下面我会逐行进行注释:
#include<bits/stdc++.h> // 引入几乎所有的C++标准库
using namespace std; // 使用标准命名空间int main() // 程序的主函数
{int n=23333333; // 01串的长度double m=11625907.5798; // 给定的信息熵// 从0试探到n,找出0的出现次数for(int ling=0; ling<=n; ling++) {int yi=n-ling; // 1出现的次数为总长度减去0出现的次数double p_ling=1.0*ling/n; // 计算0出现的概率double p_yi=1.0*yi/n; // 计算1出现的概率// 计算以0出现的概率为基础的熵部分double h_ling= - ling * p_ling *log2(p_ling);// 计算以1出现的概率为基础的熵部分double h_yi= - yi * p_yi * log2(p_yi);double h=h_ling+h_yi; // 计算总熵// 检查当前总熵h是否接近给定的信息熵m,1e-4为容差值if(fabs(h-m)<1e-4){cout<<ling; // 如果是,输出0出现的次数break; // 找到答案后结束循环}}return 0; // 程序正常结束
}
这个程序会枚举0出现的次数从0到n(串的总长度),对于每一个可能的出现次数,计算出相应的信息熵,然后与给定的信息熵m进行比较。如果计算出的信息熵与给定的信息熵在一定的误差范围内(小于 ( 1 × 1 0 − 4 ) (1 \times 10^{-4}) (1×10−4)),程序就会输出当前枚举的0的出现次数,并结束循环。
相关文章:
)
01串的熵(蓝桥杯)
文章目录 01串的熵问题描述答案:11027421题意解释暴力枚举 01串的熵 问题描述 对于一个长度为n的01串 S x 1 x 2 x 3 x_{1}x_{2}x_{3} x1x2x3… x n x_{n} xn,香农信息熵的定义为 H(S) − ∑ 1 n p ( x i ) l o g 2 ( p ( x i ) ) -\sum _{1…...

Rust 基础语法和数据类型
数据类型 Rust提供了一系列的基本数据类型,包括整型(如i32、u32)、浮点型(如f32、f64)、布尔类型(bool)和字符类型(char)。此外,Rust还提供了原生数组、元组…...

【Java SE】10 String类
目录 1. String类的重要性 2.常用方法 2.1字符串构造 2.2 String对象的比较 2.3字符串查找 2.4转化 2.5字符串替换 2.6字符串拆分 2.7字符串截取 2.8其他操作方法 2.9字符串的不可变性 2.10字符串修改 3. StringBuffer和StringBuilder 3.1StringBuilder的介绍 4.…...

web蓝桥杯真题:新鲜的蔬菜
代码: .box {display: flex; } #box1 {align-items: center;justify-content: center; }#box2 {justify-content: space-between; } #box2 .item:nth-child(2) {align-self: end; }#box3 {justify-content: space-between; } #box3 .item:nth-child(2) {align-self…...

超声波清洗机能洗哪些东西?洗眼镜超声波清洗机推荐
在现代生活中,人们对清洁卫生的要求越来越高,尤其是对一些细小物件的清洁。眼镜作为我们日常生活中不可或缺的物品,清洁保养更是至关重要。传统的清洗方式可能无法完全清洁眼镜表面的细菌和污垢,于是超声波清洗机成为了很多人的选…...
)
[C++][算法基础]走迷宫(BFS)
给定一个 nm 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。 最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意一个方…...

C语言字符串左旋
一、前言 这个题目的完整题目是这样子的。 二、我们实现这个编程的思路 2.1暴力破解思想 假如有一个数组里面的字符串为”abcdef“,我们这时候就这样先将字符”a“移到最后再将其余的字符前移。 2.2三步移动法 同样我们还是假设一个数组里面存的是字符串”abcd…...

Linux 中断会产生嵌套吗?
文章目录 1. 前言2. Linux 中断是否会嵌套?2.1 分析背景2.2 中断处理抢占、嵌套可能性分析2.3 中断处理抢占、嵌套小结 3. 参考资料 1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. …...
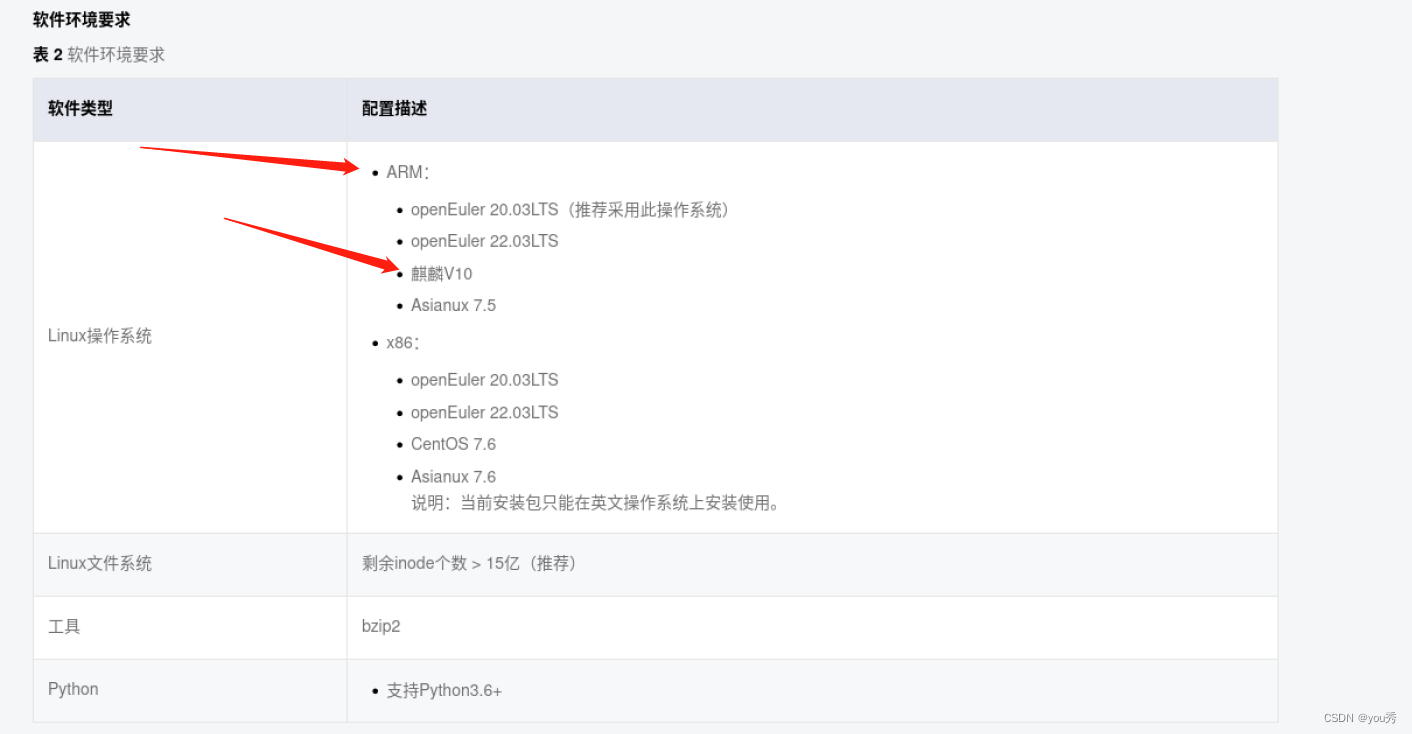
嵌入式ARM版本银河麒麟操作系统V10SP1安装OPenGauss数据库
前言: 官网提供了非常完整的openGauss安装步骤。 https://opengauss.org/zh/download/archive/列举一下个人的使用环境: 麒麟V10 rk3588工控板(ARM) openGauss-3.0.5(极简版)浏览一下官网,可以…...

深度学习八股文
Bert旨在通过联合左侧和右侧的上下文,从未标记文本中预训练出一个深度双向表示模型。因此,BERT可以通过增加一个额外的输出层来进行微调,就可以达到为广泛的任务创建State-of-the-arts 模型的效果,比如QA、语言推理任务。Bert的构…...

jquery 自整理
echarts官方:Documentation - Apache ECharts 1、CheckBox复选框 //选中事件(页面点击) $(#operateExit).on(ifChecked, function(){ $(input[name"operateExit"]).val(1); }); //非选中事件ÿ…...

MySQL | 加索引报错
报错信息 1170 - BLOB/TEXT column user_name used in key specification without a key length解决方案 分析 这个错误通常是因为尝试在一个包含BLOB或TEXT类型列的列上创建索引时没有指定键的长度。MySQL要求在使用BLOB或TEXT类型列作为索引键时,必须指定键的长…...

前端:自制年历
详细思路可以看我的另一篇文章《前端:自制月历》,基本思路一致,只是元素布局略有差异 ①获取起始位startnew Date(moment().format(yyyy-01-01)).getDay() ②获取总的格子数numMath.ceil(365/7)*7,这里用365或者366计算结果都是一样的371 …...

9.手写JavaScript大数相加问题
一、核心思想 找到两个字符串中最长的长度,对两个字符串在头位置补0达到相等的长度,相加时注意进位和类型转换,特别考虑当相加到第一位是如果仍然有进位不要忽略。此外,js中允许使用的最大的数字为 console.log("最大数&qu…...
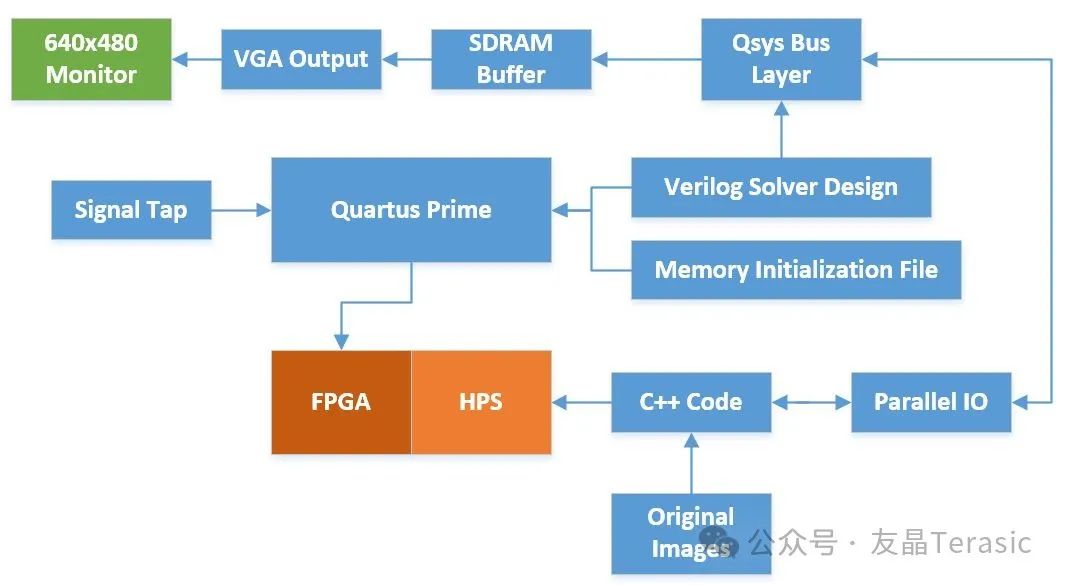
FPGA开源项目分享——基于 DE1-SOC 的 String Art 实现
导语 今天继续康奈尔大学FPGA课程ECE 5760的典型案例分享——基于DE1-SOC的String Art实现。 (更多其他案例请参考网站: Final Projects ECE 5760) 1. 项目概述 项目网址 ECE 5760 Final Project 项目说明 String Art起源于19世纪的数学…...

通过 CLI 和引入的方式使用 React:基础入门
使用React 有两种使用方式,主要有以下几个原因: 灵活性和适应性: 引入的方式可以让开发者在现有的 HTML 页面中快速引入 React,无需设置完整的项目环境。这适合小型或原型项目。 CLI 方式则更适合用于构建大型复杂的 React 应用程序,因为它提供了更完整的项目结构和…...

第三资本:铸就辉煌非凡的资历
第三资本香港有限公司在在金融投资领域一直以专业精神和不懈追求获得良好名声,近几年在国际资本市场上更是写下了辉煌的章节。针对第三资本而言,专业是基本,也是成功的唯一途径。投资总监刘国海解释道:“金融从业者务必深入把握专业能力,对行业现状敏感,重视风险管控,才能在这个…...

基于激光雷达的袋装水泥智能装车系统有哪些优势?
激光雷达技术在水泥机械智能化中发挥着举足轻重的作用,特别在袋装水泥智能装车系统的应用中表现得尤为突出。 由因泰立科技精心打造的基于激光雷达的袋装水泥智能装车系统,不仅大幅缩短了装车码垛的时间,降低了工人的劳动强度,还显…...

实战自动化修改主机名
一、主程序 #!/bin/bash# 设置主机名为node01 set_hostname() {local new_hostname$1echo "正在设置主机名为 $new_hostname ..."# 使用hostnamectl设置主机名hostnamectl set-hostname $new_hostname# 检查主机名是否更改成功if [ "$(hostname)" "…...
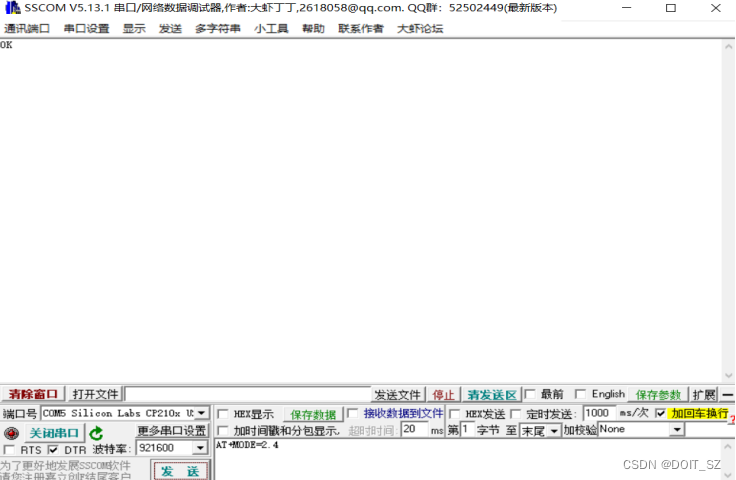
无人机GB42590接收端 +接收端,同时支持2.4G与5.8G双频WIFI模组
严格按照GB42590的协议开发的发射端,通过串口和模块通讯,默认波特率 921600。 http://www.doit.am/首页-深圳四博智联科技有限公司-淘宝网https://shop144145132.taobao.com/?spma230r.7195193.1997079397.2.71f6771dJHT2r0 二、接口文档 单片机和模…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
