C语言程序设计每日一练(1)
探索数字组合的奇妙世界:如何生成所有独特的三位数
当我们想要探索由1、2、3、4这四个数字能组成多少个不同的三位数时,我们实际上是在解决一个排列组合的问题。这不仅是一个数学问题,也是编程领域经常遇到的挑战,特别是在数据处理、密码学或算法设计中。
问题分析
为了解决这个问题,我们首先要理解题目的核心要求:
- 互不相同:每个数字在三位数中只能出现一次。
- 无重复数字:任意两个不同的三位数之间,不能出现完全相同的数字组合。
考虑到这两个要求,我们可以通过三重循环来生成所有可能的三位数组合。每一位(百位、十位、个位)都可以是1、2、3、4中的任意一个数字,但我们需要确保在同一组合中,这三个位置的数字各不相同。
程序解读
下面的C语言程序就是基于上述思路编写的:
#include <stdio.h> int main()
{ int i, j, k; printf("\n"); for (i = 1; i < 5; i++) /* 百位 */ for (j = 1; j < 5; j++) /* 十位 */ for (k = 1; k < 5; k++) /* 个位 */ { if (i != k && i != j && j != k) /* 确保i、j、k三位互不相同 */ printf("%d%d%d\n", i, j, k); /* 输出组合 */ } return 0;
}在这段代码中,我们使用了三重循环来遍历1到4这四个数字。if语句确保三个位置上的数字都是不同的,只有满足这个条件,才会输出这个组合。
输出结果与总结
运行这段程序,你会得到所有由1、2、3、4组成的、无重复数字的三位数。这些数字在密码学、统计学和数据科学中都有重要的应用。通过编程,我们不仅可以解决这类具体的数学问题,还可以更深入地理解排列组合的原理,并将其应用于更广泛的领域。
此外,这个程序也展示了循环和条件语句在编程中的基础而重要的应用。对于初学者来说,这是一个很好的练习和理解编程基础概念的机会。通过简单的修改,这个程序还可以用于解决其他类似的问题,比如生成所有可能的、由特定数字组成的其他长度的数字串等。
总的来说,这个程序不仅解决了一个具体的数学问题,还展示了编程在解决排列组合问题中的灵活性和实用性。通过编写和执行这样的程序,我们可以更深入地理解数字、编程和逻辑之间的关系。
算法详解
-
初始化:算法开始时,我们定义了三个循环变量
i,j,k,分别代表三位数的百位、十位和个位数字。 -
三重循环:
- 外层循环(
i循环)遍历1到4,代表三位数百位上的数字。 - 中间循环(
j循环)同样遍历1到4,代表十位数。 - 内层循环(
k循环)也是遍历1到4,代表个位数。
- 外层循环(
-
条件判断:在每次内层循环中,都会检查
if (i != k && i != j && j != k)这个条件,以确保三个位置上的数字互不相同。这是满足题目要求“互不相同且无重复数字”的关键步骤。 -
输出结果:如果满足上述条件,则输出这个三位数。注意,在输出时,我们直接将
i,j,k连接成一个数字输出,而不是以逗号分隔。因此,在实际代码中,应该将printf("%d,%d,%d\n",i,j,k);修改为printf("%d%d%d\n",i,j,k);以避免输出错误。
算法复杂度
-
时间复杂度:
-
由于我们有三重循环,每重循环最多执行4次(数字1到4),所以总的时间复杂度是O(n^3),在这里n=4,因此是O(64)。但实际上,因为数字是固定的(1,2,3,4),所以时间复杂度可以看作是常量的,即O(1)。然而,如果问题扩展到更大的数字范围,时间复杂度将随数字数量的增加而立方级增长。
-
空间复杂度:
-
此算法仅使用了几个整型变量来存储当前的数字组合,并没有使用额外的数据结构来存储结果或中间数据。因此,其空间复杂度是O(1),即常量空间。
优化与扩展
虽然这个算法对于当前的问题是有效的,但如果我们需要处理更大的数字范围或更多的位数,它可能就会变得非常低效。在这种情况下,我们可以考虑使用更高效的算法,如回溯法或动态规划,来生成所有可能的组合。
此外,如果我们只需要知道有多少种组合而不是具体的组合是什么,我们可以使用组合数学中的排列公式来计算。对于这个问题,由于我们有4个不同的数字,并且我们要选择3个来组成一个三位数,所以总的排列数就是4的阶乘除以(4-3)的阶乘,即4!/1! = 24种不同的组合。
相关文章:
)
C语言程序设计每日一练(1)
探索数字组合的奇妙世界:如何生成所有独特的三位数 当我们想要探索由1、2、3、4这四个数字能组成多少个不同的三位数时,我们实际上是在解决一个排列组合的问题。这不仅是一个数学问题,也是编程领域经常遇到的挑战,特别是在数据处…...

Spring 统一功能处理
前言:为什么要有统一功能处理? 我们在进行数据的返回的时候,不同的方法返回的数据类型也不一样,但是我们前端有时候期望拿到是一样的数据类型。就好比买菜的时候期望最后是用一个大的塑料袋进行包装的。 那么我们可以在HTTP进行响应的之前,做一些事情,让我们返回的数据统…...

【软设】知识点速记2
1.安全性、可靠性与系统性能评测基础知识 1.1计算机和网络安全 1.1.1 安全威胁 网络安全威胁是指任何可能损害网络系统的保密性、完整性和可用性的因素或行为。这些威胁可能来自内部或外部,包括恶意软件、信息泄露、DDoS攻击、社交工程、网络钓鱼、黑客攻击和资源滥用等多种…...

激光雷达和相机的联合标定工具箱[cam_lidar_calibration]介绍
激光雷达和相机的联合标定工具箱[cam_lidar_calibration]介绍 写在前面安装过程调试过程标定成功可视化展示 写在前面 激光雷达和相机联合标定工具 论文地址:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber9564700 github地址: https://github.com…...
ML.NET(二) 使用机器学习预测表情分析
这个例子使用模型进行表情分析: 准备数据: happy,sad 等; using Common; using ConsoleApp2; using Microsoft.ML; using Microsoft.ML.Data; using System.Diagnostics; using static Microsoft.ML.Transforms.ValueToKeyMappingEstimator;…...

YOLOv9最新改进系列:YOLOv9改进之添加注意力-ContextAggregation,有效涨点!!!
YOLOv9最新改进系列:YOLOv9改进之添加注意力-ContextAggregation,有效涨点!!! YOLOv9原文链接戳这里,原文全文翻译请关注B站Ai学术叫叫首er B站全文戳这里! 详细的改进教程以及源码ÿ…...

【数据结构】初识数据结构与复杂度总结
前言 C语言这块算是总结完了,那从本篇开始就是步入一个新的大章——数据结构,这篇我们先来认识一下数据结构有关知识,以及复杂度的相关知识 个人主页:小张同学zkf 若有问题 评论区见 感兴趣就关注一下吧 目录 1.什么是数据结构 2.…...

子域名是什么?有什么作用?
在互联网世界中,域名是我们访问网站的关键。每一个公司的网站都需要拥有自己的域名,其中有些大型公司的网站还不止一个域名,除了主域名外还拥有子域名。有些人感到非常困惑,不知道子域名是什么。其实子域名也就是平时所说的二级域…...

学习 Rust 的第一天:基础知识
如果你对 Rust 一无所知,那我来解释一下。 “Rust 是一种系统编程语言,其优先考虑性能、内存安全和零成本抽象。” 你好,世界 我之前研究过 Rust,并且对 Java、C、C 和 Python 的基本编程概念有相当了解。 今天,我…...

电商技术揭秘七:搜索引擎中的SEO关键词策略与内容优化技术
文章目录 引言一、关键词策略1.1 关键词研究与选择1. 确定目标受众2. 使用关键词研究工具3. 分析搜索量和竞争程度4. 考虑长尾关键词5. 关键词的商业意图6. 创建关键词列表7. 持续监控和调整 1.2 关键词布局与密度1. 关键词自然分布2. 标题标签的使用3. 首次段落的重要性4. 关键…...
系统开发实训小组作业week7 —— 优化系统开发计划
目录 1. 建立规则,仪式,流程,模式 2. 给好行为正面的反馈 3. 明确指出不合适的行为,必要时调整人员 在 “系统开发实训课程” 中,我们小组的项目是 “电影院会员管理系统” 。在项目的开发过程中,我们遇…...
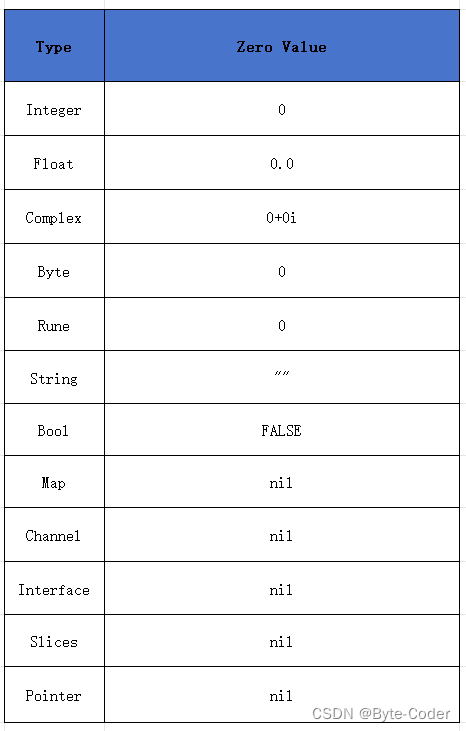
golang的引用和非引用总结
目录 概述 一、基本概念 指针类型(Pointer type) 非引用类型(值类型) 引用类型(Reference Types) 解引用(dereference) 二、引用类型和非引用类型的区别 三、golang数据类型…...

2024认证杯数学建模B题思路模型代码
目录 2024认证杯数学建模B题思路模型代码:4.11开赛后第一时间更新,获取见文末名片 第十三届“认证杯”数学中国数学建模比赛赛后体会 2024认证杯数学建模B题思路模型代码:4.11开赛后第一时间更新,获取见文末名片 第十三届“认证杯”数学中国数学建模比…...

一种快速移植 OpenHarmony Linux 内核的方法
移植概述 本文面向希望将 OpenHarmony 移植到三方芯片平台硬件的开发者,介绍一种借助三方芯片平台自带 Linux 内核的现有能力,快速移植 OpenHarmony 到三方芯片平台的方法。 移植到三方芯片平台的整体思路 内核态层和用户态层 为了更好的解释整个内核…...

java的jar包jakarta.jakartaee-web-api和jakarta.servlet-api有什么区别
jakarta.jakartaee-web-api和jakarta.servlet-api都是Java EE(现在是 Jakarta EE)中的一部分,用于开发基于Java EE平台的Web应用程序。它们之间的区别在于以下几点: 命名空间: jakarta.servlet-api是Java EE 8之前版本…...

QT_day2
使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 将登录按钮使用qt4版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin",密码是否为…...
Advanced RAG 02:揭开 PDF 文档解析的神秘面纱
编者按: 自 2023 年以来,RAG 已成为基于 LLM 的人工智能系统中应用最为广泛的架构之一。由于诸多产品的关键功能(如:领域智能问答、知识库构建等)严重依赖RAG,优化其性能、提高检索效率和准确性迫在眉睫&am…...

Spring面试题pro版-1
Spring框架是由于软件开发的复杂性而创建的。Spring使用的是基本的JavaBean来完成以前只可能由EJB完成的事情。然而,Spring的用途不仅仅限于服务器端的开发。从简单性、可测试性和松耦合性角度而言,绝大部分Java应用都可以从Spring中受益。 Spring是什么…...

6 Reverse Linked List
分数 20 作者 陈越 单位 浙江大学 Write a nonrecursive procedure to reverse a singly linked list in O(N) time using constant extra space. Format of functions: List Reverse( List L ); where List is defined as the following: typedef struct Node *PtrToNo…...

【随笔】Git 高级篇 -- 相对引用2 HEAD~n(十三)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
