概率论基础——拉格朗日乘数法
概率论基础——拉格朗日乘数法
概率论是机器学习和优化领域的重要基础之一,而拉格朗日乘数法与KKT条件是解决优化问题中约束条件的重要工具。本文将简单介绍拉格朗日乘数法的基本概念、应用以及如何用Python实现算法。
1. 基本概念
拉格朗日乘数法是一种用来求解带约束条件的优化问题的方法。它将约束优化问题转化为一个无约束优化问题,并通过引入拉格朗日乘数来实现。拉格朗日乘数法的核心思想是在原始优化问题的基础上,引入拉格朗日乘子构造一个新的拉格朗日函数,然后通过对该函数求导,找到极值点,从而得到原始优化问题的解。
2. 拉格朗日乘数法
考虑带约束条件的优化问题:
minimize f ( x ) subject to g i ( x ) ≤ 0 , i = 1 , 2 , … , m h j ( x ) = 0 , j = 1 , 2 , … , p \begin{align*} \text{minimize} & \quad f(x) \\ \text{subject to} & \quad g_i(x) \leq 0, \quad i = 1, 2, \ldots, m \\ & \quad h_j(x) = 0, \quad j = 1, 2, \ldots, p \end{align*} minimizesubject tof(x)gi(x)≤0,i=1,2,…,mhj(x)=0,j=1,2,…,p
其中,(f(x))是目标函数,(g_i(x))是不等式约束,(h_j(x))是等式约束。使用拉格朗日乘数法,我们可以构造拉格朗日函数:
L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ j = 1 p μ j h j ( x ) L(x, \lambda, \mu) = f(x) + \sum_{i=1}^{m} \lambda_i g_i(x) + \sum_{j=1}^{p} \mu_j h_j(x) L(x,λ,μ)=f(x)+i=1∑mλigi(x)+j=1∑pμjhj(x)
其中, λ i \lambda_i λi和 μ j \mu_j μj是拉格朗日乘子。然后,通过对拉格朗日函数求梯度,并令梯度等于零,我们可以求解极值点。这些点可能是潜在的最小值、最大值或鞍点。
3. 等式约束优化问题
对于只有等式约束的优化问题,我们可以使用拉格朗日乘数法来求解。考虑如下形式的优化问题:
minimize f ( x ) subject to h ( x ) = 0 \begin{align*} \text{minimize} & \quad f(x) \\ \text{subject to} & \quad h(x) = 0 \end{align*} minimizesubject tof(x)h(x)=0
构造拉格朗日函数:
L ( x , λ ) = f ( x ) + λ h ( x ) L(x, \lambda) = f(x) + \lambda h(x) L(x,λ)=f(x)+λh(x)
然后,求解梯度等于零的方程组:
∇ x L ( x , λ ) = 0 and ∇ λ L ( x , λ ) = 0 \nabla_x L(x, \lambda) = 0 \quad \text{and} \quad \nabla_\lambda L(x, \lambda) = 0 ∇xL(x,λ)=0and∇λL(x,λ)=0
4. 不等式约束优化问题
对于带有不等式约束的优化问题,我们也可以使用拉格朗日乘数法。考虑如下形式的优化问题:
minimize f ( x ) subject to g ( x ) ≤ 0 \begin{align*} \text{minimize} & \quad f(x) \\ \text{subject to} & \quad g(x) \leq 0 \end{align*} minimizesubject tof(x)g(x)≤0
构造拉格朗日函数:
L ( x , λ ) = f ( x ) + λ g ( x ) L(x, \lambda) = f(x) + \lambda g(x) L(x,λ)=f(x)+λg(x)
然后,求解梯度等于零的方程:
∇ x L ( x , λ ) = 0 and λ g ( x ) = 0 \nabla_x L(x, \lambda) = 0 \quad \text{and} \quad \lambda g(x) = 0 ∇xL(x,λ)=0andλg(x)=0
用Python实现算法
下面我们用Python实现一个简单的带等式约束的优化问题,并使用拉格朗日乘数法求解。
import numpy as np
from scipy.optimize import minimize# 定义目标函数
def objective(x):return (x[0] - 1) ** 2 + (x[1] - 2) ** 2# 定义等式约束函数
def constraint(x):return x[0] + x[1] - 3# 定义初始猜测值
x0 = np.array([0, 0])# 使用minimize函数求解
solution = minimize(objective, x0, constraints={'type': 'eq', 'fun': constraint})# 输出结果
print("Optimal solution:", solution.x)
print("Objective value at the solution:", solution.fun)

总结
拉格朗日乘数法是解决带约束条件的优化问题的重要方法之一。通过引入拉格朗日乘子,我们可以将原始问题转化为无约束问题,并通过求解新的拉格朗日函数的极值点来得到原始问题的解。然而,拉格朗日乘数法并不保证得到全局最优解,因此在实际应用中需要结合其他方法进行优化。
相关文章:

概率论基础——拉格朗日乘数法
概率论基础——拉格朗日乘数法 概率论是机器学习和优化领域的重要基础之一,而拉格朗日乘数法与KKT条件是解决优化问题中约束条件的重要工具。本文将简单介绍拉格朗日乘数法的基本概念、应用以及如何用Python实现算法。 1. 基本概念 拉格朗日乘数法是一种用来求解…...

[xboard]real6410-6.2 移植kernel网络驱动
文章目录 硬件电路软件配置问题1问题2问题3问题4功能测试硬件电路 核心板,使用DM9000A [图片] 软件配置 问题1 / # / # ifconfig ifconfig: /proc/net/dev: No such file or directory ifconfig: socket: Fun...

Quarkus初探
Quarkus初探 背景安装Quarkus安装Quarkus CLI 创建Quarkus项目运行Quarkus初探代码修改一下代码 数据持久化创建PanacheEntiry写入数据读取数据 Dev Service使用外部数据库区分dev和prod 构建native应用(依赖Graalvm) 背景 最早是在Infoq上了解到Quarku…...

90天玩转Python-02-基础知识篇:初识Python与PyCharm
90天玩转Python系列文章目录 90天玩转Python—01—基础知识篇:C站最全Python标准库总结 90天玩转Python--02--基础知识篇:初识Python与PyCharm 90天玩转Python—03—基础知识篇:Python和PyCharm(语言特点、学习方法、工具安装&…...
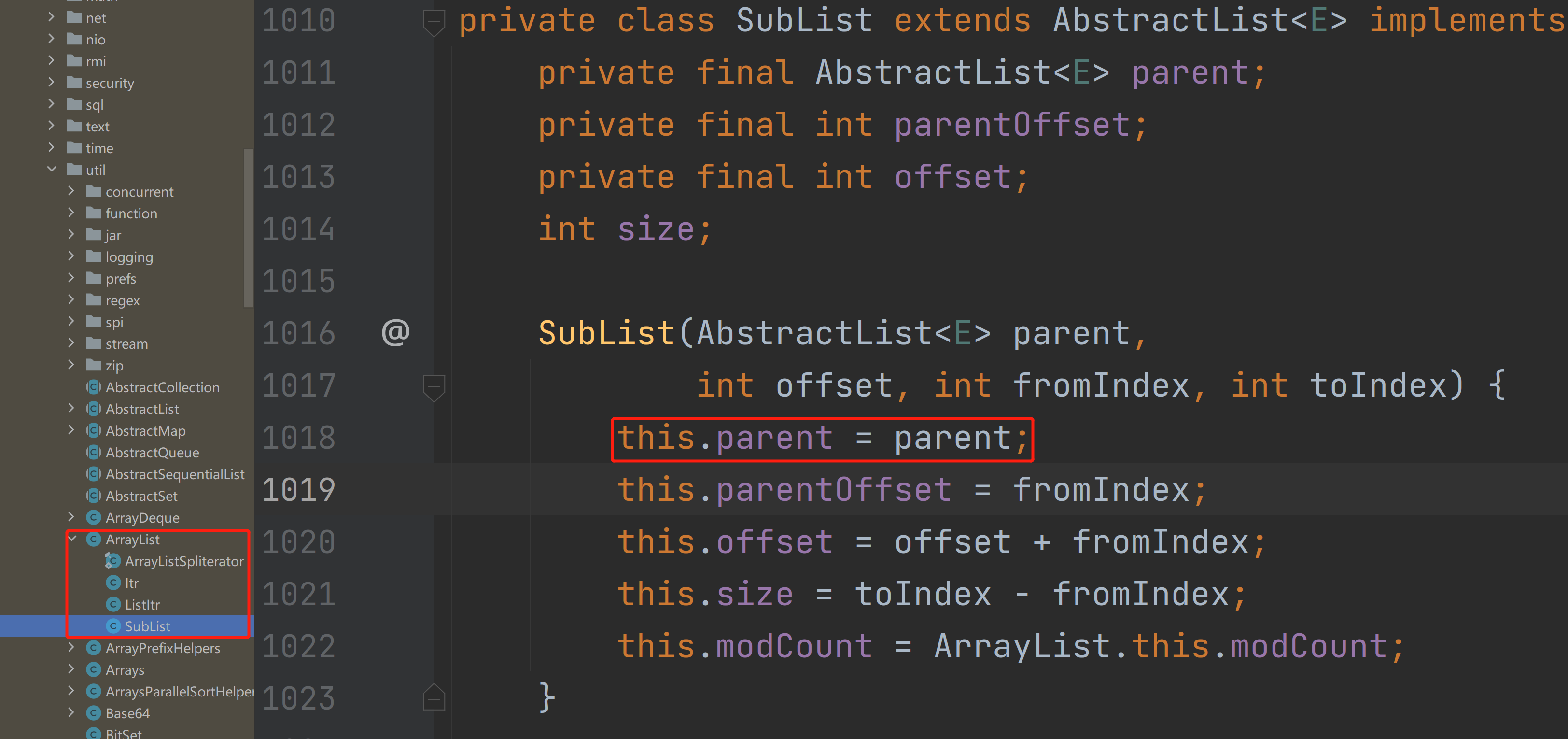
List操作的一些常见问题
1. Arrays.asList转换基本类型数组 在实际的业务开发中,我们通常会进行数组转List的操作,通常我们会使用Arrays.asList来进行转换,但是在转换基本类型的数组的时候,却出现转换的结果和我们想象的不一致。 import java.util.Arra…...

如何使用Java和RabbitMQ实现延迟队列?
前言 今天我们使用Java和RabbitMQ实现消息队列的延迟功能。 前期准备,需要安装好docker、docker-compose的运行环境。 需要安装RabbitMQ的可以看下面这篇文章。 如何使用PHP和RabbitMQ实现消息队列?-CSDN博客 今天讲的是依赖RabbitMQ的延迟插件实现…...

AI论文速读 | TF-LLM:基于大语言模型可解释性的交通预测
论文标题: Explainable Traffic Flow Prediction with Large Language Models 作者:Xusen Guo, Qiming Zhang, Mingxing Peng, Meixin Zhu(朱美新)*, Hao (Frank)Yang(杨昊) 机构:香港科技大学(广州),约翰…...

智慧矿山视频智能监控与安全监管方案
一、行业背景 随着全球能源需求的日益增长,矿业行业作为国民经济的重要支柱,其发展日益受到广泛关注。然而,传统矿山管理模式的局限性逐渐显现,如生产安全、人员监管、风险预警等方面的问题日益突出。因此,智慧矿山智…...
2024春算法训练4——函数与递归题解
一、前言 感觉这次的题目都很好,但是E题....(我太菜了想不到),别人的题解都上百行了,晕; 二、题解 A-[NOIP2010]数字统计_2024春算法训练4——函数与递归 (nowcoder.com) 这种题目有两种做法:…...

【C++】C++知识点复习
牛客cpp:牛客网在线编程 2024年4月10日:BC1—>BC8 BC4:浮点数精度保留 问题:不加入fixed输入0.359813,最后得到0.36,并不是强制保留0.360。这种写法会保留小数点后三位精度,但是最后输出会省略掉最后…...

SpringBoot+Vue,轻松实现网页版人脸登录与精准识别
目录 1、技术介绍 2、技术原理 2.1、人脸检测 ①参考模板法 ②人脸规则法 2.2、人脸跟踪 2.3、人脸比对 ①特征向量法 ②面纹模板法 识别过程 案例 一、springboot后端项目 1,拉取项目后,导入相关依赖jar包 2,执行sql文件夹下面…...

深入浅出 -- 系统架构之垂直架构
当业务复杂度增加、访问量逐渐增大出现高并发时,单体架构无法满足需求,可以根据业务功能对系统进行拆分,以提高访问效率。 垂直架构介绍 1.垂直架构一般是因为单体架构太过于庞大而进行的拆分,拆分后各个系统应满足独立运行互相不…...
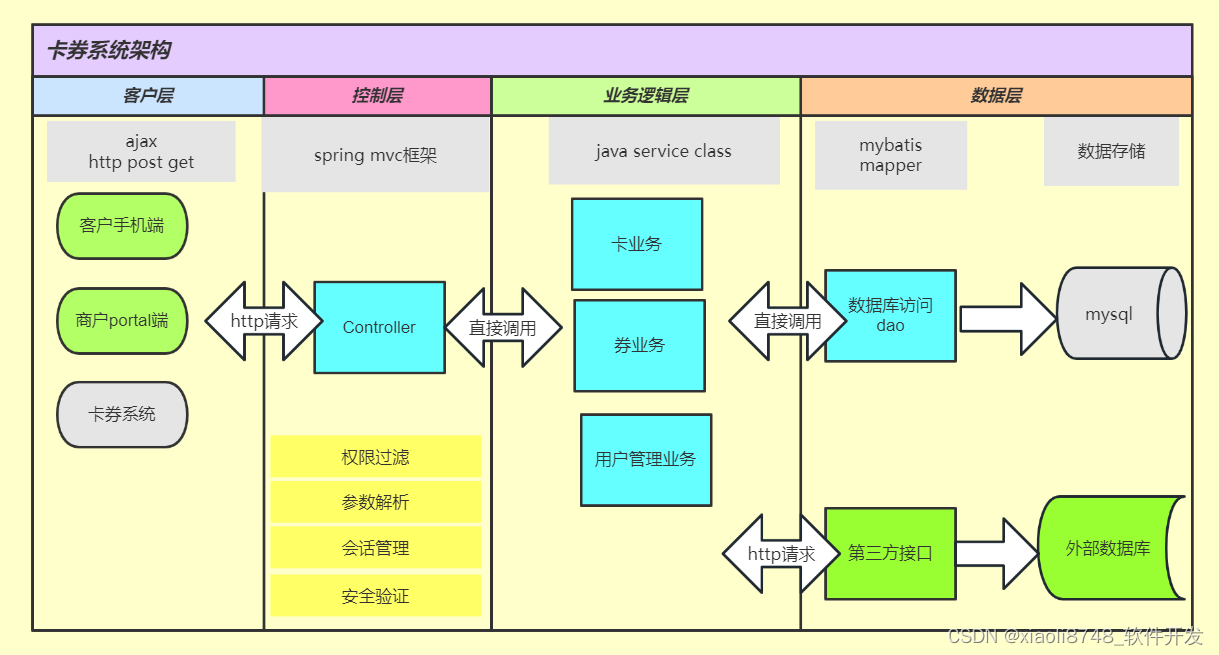
深入浅出 -- 系统架构之微服务架构选型参考图
技术选型架构图 是一个用于展示项目中所采用的各种技术和组件之间关系的图表。 它通常包括以下几个部分: 1. 项目名称和描述:简要介绍项目的背景和目标。 2. 技术栈:列出项目中使用的主要技术和工具,如编程语言、框架、数据库…...

Java 使用 ant.jar 执行 SQL 脚本文件
Java 使用 ant.jar 执行 SQL 脚本文件,很简单。 在 pom.xml 中导入 ant 依赖 <dependency><groupId>org.apache.ant</groupId><artifactId>ant</artifactId><version>1.10.11</version> </dependency>sql 脚本文件…...

【随笔】Git 高级篇 -- 快速定位分支 ^|~(二十三)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...

git环境切换
文章目录 一. 操作步骤:1.查看全局设置3.Git 切换本地git设置4.切换仓库并推送 一. 操作步骤: 1.查看全局设置 $ Git config --global --list credential.https://codeup.aliyun.com.providergeneric user.namebiejiahao user.emailxxxxxxxxqq.com3.Gi…...

hyperf websocket
composer require hyperf/websocket-server 配置 Server 修改 config/autoload/server.php,增加以下配置。 <?phpreturn [servers > [[name > ws,type > Server::SERVER_WEBSOCKET,host > 0.0.0.0,port > 9502,sock_type > SWOOLE_SOCK_TCP…...

用Echarts词云数据可视化热词表白
目录 1、使用前准备 2、准备工作 3、盒子搭建 4、整体展现 1、使用前准备 找到表白对象(重中之重!),不要一见钟情(个人觉得:一见钟情属于见色起意!),因为数据可视化需…...

VUE 实现路由的基本原理
路由 基本概念 在前端技术早期,所有页面的跳转通过更改url,浏览器页面刷新获取新的页面内容,这种粗糙的交互方式,一直等待优化。 后来,改变发生了——Ajax 出现了,它允许人们在不刷新页面的情况下发起请求࿰…...

Android 11 添加系统属性
在初识Android 属性一文中提到,系统会默认加载以下文件 /system/etc/prop.default /system/build.prop /system_ext/build.prop /vendor/default.prop /vendor/build.prop /odm/etc/build.prop /product/build.prop /factory/factory.prop要弄清楚我们应该在哪里添…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
