逻辑回归都有什么类型
逻辑回归是一种用于解决分类问题的统计学习方法,它基于概率理论,将输入特征与输出类别之间的关系建模为一个概率分布。逻辑回归模型可以用不同的方法来表示,其中包括:
1. **基本逻辑回归模型**:最简单的逻辑回归模型假设输出是由输入特征的线性组合经过一个sigmoid函数(也称为逻辑函数)转换得到的,常见的形式如下:
\[ P(y=1 | \mathbf{x}) = \frac{1}{1 + e^{-\mathbf{w}^T\mathbf{x} - b}} \]
2. **多项式逻辑回归**:当特征之间的关系不是线性的时候,可以考虑使用多项式逻辑回归,通过引入高阶项来拟合数据。
3. **正则化逻辑回归**:为了防止过拟合,可以在逻辑回归模型中引入正则化项,常见的有L1正则化和L2正则化,得到的模型分别称为L1逻辑回归和L2逻辑回归。
4. **多分类逻辑回归**:逻辑回归最初是用于二分类问题的,但是可以通过一对多(one-vs-rest)或者多对多(many-vs-many)的策略来解决多分类问题。
5. **逻辑回归树**:逻辑回归树是一种结合了决策树和逻辑回归的方法,它通过构建决策树来对输入数据进行分段,然后在每个叶节点上应用逻辑回归模型。
6. **贝叶斯逻辑回归**:贝叶斯逻辑回归将贝叶斯思想引入逻辑回归模型中,通过对参数引入先验分布来进行参数估计。
以上是逻辑回归模型的一些常见形式,根据具体的问题和数据特点,可以选择合适的模型来建模和预测。
不同类型的逻辑回归模型在应用场景上有所差异,下面是它们各自的主要使用场景:
1. **基本逻辑回归模型**:
- 适用于二分类问题,特征与输出之间的关系近似为线性关系时效果较好。
- 例如:垃圾邮件分类、疾病诊断等。
2. **多项式逻辑回归**:
- 适用于特征之间存在高阶关系时,能够更好地拟合非线性数据。
- 例如:图像分类、自然语言处理中的情感分析等。
3. **正则化逻辑回归**:
- 适用于数据特征较多、容易过拟合的情况,通过加入正则化项可以提高模型的泛化能力。
- 当数据量较小或者特征之间存在共线性时,也可以考虑使用正则化逻辑回归。
- 例如:金融风控中的信用评分模型、文本分类等。
4. **多分类逻辑回归**:
- 适用于多分类问题,可以通过一对多或多对多的策略来解决。
- 例如:手写数字识别、文本分类等。
5. **逻辑回归树**:
- 适用于数据具有明显分段特点的情况,能够更好地捕捉数据的非线性关系。
- 例如:客户流失预测、信用评分模型等。
6. **贝叶斯逻辑回归**:
- 适用于需要考虑参数的先验分布情况,以及需要进行参数估计的情况。
- 例如:医学诊断、金融风险评估等。
根据数据的特点、问题的要求以及模型的复杂度等因素,可以选择适合的逻辑回归模型来建立分类模型。
相关文章:

逻辑回归都有什么类型
逻辑回归是一种用于解决分类问题的统计学习方法,它基于概率理论,将输入特征与输出类别之间的关系建模为一个概率分布。逻辑回归模型可以用不同的方法来表示,其中包括: 1. **基本逻辑回归模型**:最简单的逻辑回归模型假…...

基于springboot+vue实现的高校宿舍管理系统(界面优美,十分推荐)
一、项目简介 本项目是一套基于springbootvue实现的高校宿舍管理系统设计与实现 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观…...

C语言学习笔记day18
1. 指针基本概念 1.地址:用来区分内存中不同字节的编号 2.指针:地址就是指针,指针就是地址 3.指针变量:存储指针的变量,有时去掉变量,称为指针 2. 指针运算符 1.&: 1.获得一个变量在内存空间中的首地址 2.让表达式类型升级 2.*: 1.取…...

JSP内置对象session
1.session对象,为会话对象,封装当前用户会话中的有关信息。 网页数据传递是单向传递的,session能够将数据进行多个数据互相传递,使用的是同一个东西 实例1: 利用session对象String getId() 方法获取当前session对象…...

BM96 主持人调度(二)(贪心算法)
一开始写的时候忘了给start、end数组赋值了 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 计算成功举办活动需要多少名主持人* param n int整型 有n个活动* param start…...
【TB作品】MSP430单片机读取大气压强传感器BMP180
文章目录 实物main所有代码 实物 main #include <msp430.h> #include "stdio.h" #include "OLED.h"#include <stdio.h> #include <stdlib.h> #include <string.h> #include <math.h>// P2.2 oled scl // P2.3 oled sda// p…...
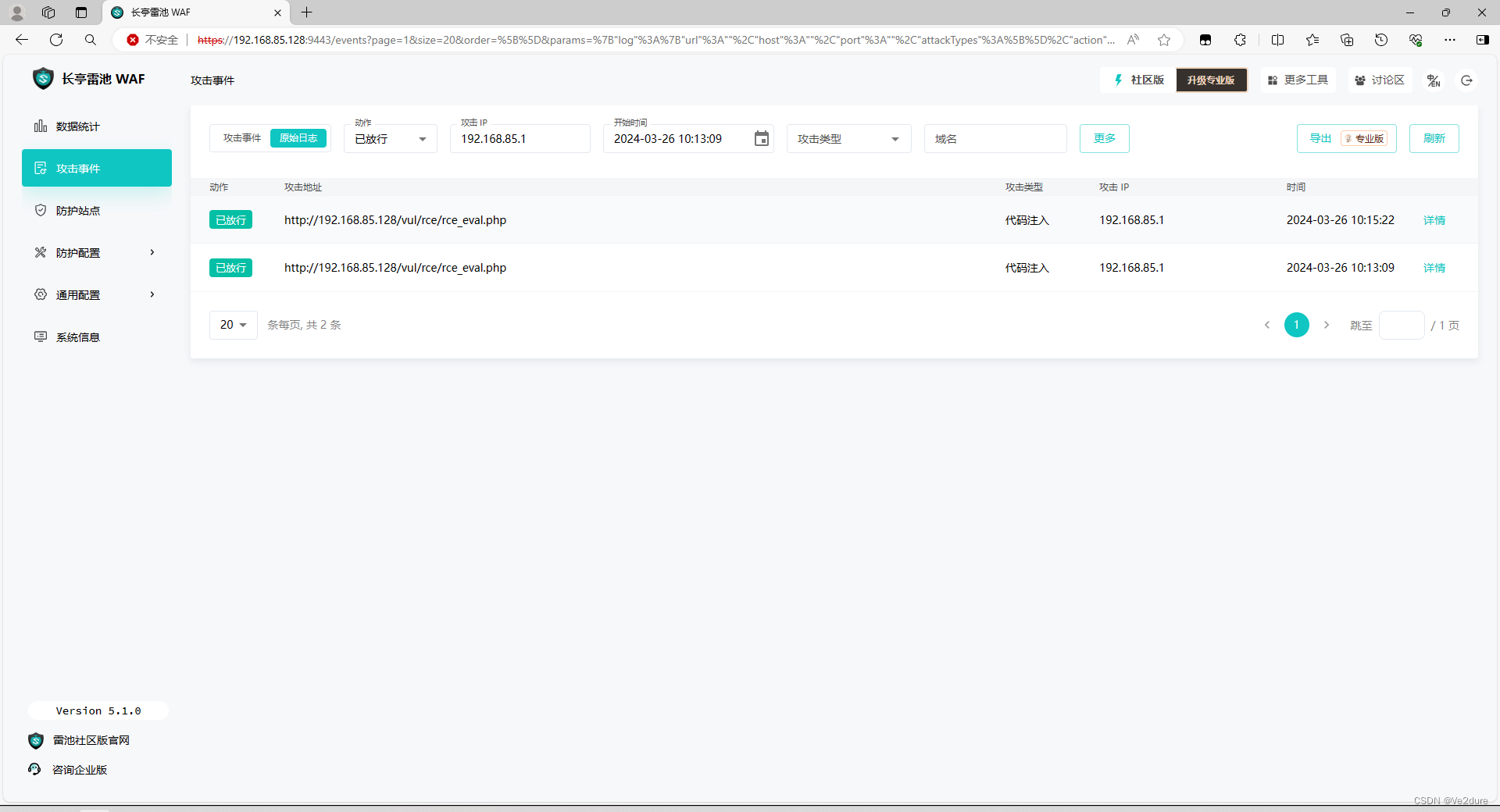
Github第一Star数的国产免费开源防火墙--雷池社区版初步体验
前言 近期准备搭建一个博客网站,用来存储工作室同学们的学习笔记。服务器准备直接放在公网上,方便大家随时随地的上传和浏览,为了防止网站被人日穿成为肉鸡,一些防御措施还是要部署的。 首先明确自己的需求: 零成本…...

自动驾驶涉及相关的技术
自动驾驶涉及多种技术,包括传感器、数据处理、决策制定和执行控制等方面。以下是一些关键技术的详细说明: 传感器技术: 激光雷达(LiDAR):激光雷达通过发射激光束并测量其反射时间来获取周围环境的高精度三维…...

简单高效的GO发票识别+发票查验接口
在这个瞬息万变的商业世界里,商业欺诈如影随形,虚假发票成为企业难以忽视的风险。而发票作为每笔交易的重要凭证,对其进行入账前的真伪查验显得尤为重要。但面对海量的发票查验与发票录入工作,人工手动查验的方式,速度…...

c++和python基本数据类型比较
以下是 C 和 Python 中一些基本数据类型的比较: 1. 整数类型: C: C 中的整数类型包括 int, short, long, long long 等,它们的大小和范围取决于编译器和操作系统。 Python: Python 中只有一个整数类型 int࿰…...
运维工具如此割裂,九招帮你统一纳管
背景 在运维工具这个江湖中,出现了众多独行侠客,各怀绝技,各自为战。这些开源监控软件如同武林中的各派门派:SkyWalking 以精湛的追踪功夫独步武林;Prometheus 以灵活的告警机制纵横江湖;ELK 则如同黯然销…...

基于springboot的大创管理系统源码数据库
基于springboot的大创管理系统源码数据库 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了大创管理系统的开发全过程。通过分析大创管理系统管理的不足,创建了一个计算机管理大创管理系统的方案。…...
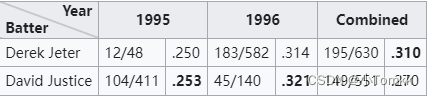
解密辛普森悖论:如何在数据分析中保持清醒头脑
解密辛普森悖论:如何在数据分析中保持清醒头脑 之前也参加fine Bi的 培训,学到了辛普森悖论,今天为大家介绍一下 文章目录 解密辛普森悖论:如何在数据分析中保持清醒头脑前言我们来举一个例子数据分析解释管理应用的启示 前言 什…...

Vue前端框架
1.vue基本使用1 1.vue环境搭建 一般创建vue项目是在cmd命令中用:vue ui 命令,采用ui图形界面的方式直观创建项目。 2.vue基本使用方式:vue组件 3.文本插值 4.属性绑定 5.事件绑定 6.双向绑定 7.条件渲染 2.vue基本使用2 1.axios 安装axios命令…...

【随笔】Git 基础篇 -- 远程仓库 git clone(二十五)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...
?)
在js中如果a的值是空是不是if(表达式的值是false)?
在JavaScript中,一个变量的“空”值可以有多种含义,具体取决于该变量的类型和内容。对于if语句中的条件表达式,其值会被隐式地转换为布尔值。以下是JavaScript中常见的“空”值以及它们在布尔上下文中的行为: null:在…...

数据生成 | Matlab实现基于K-means和SVM的GMM高斯混合分布的数据生成
数据生成 | Matlab实现基于K-means和SVM的GMM高斯混合分布的数据生成 目录 数据生成 | Matlab实现基于K-means和SVM的GMM高斯混合分布的数据生成生成效果基本描述模型描述程序设计参考资料 生成效果 基本描述 1.Matlab实现基于K-means和SVM的GMM高斯混合分布的数据生成…...
HarmonyOS开发:【NFC配置流程】
一、简介 碰一碰是HarmonyOS具备的多终端业务协同技术。其依托NFC短距通信协议,通过碰一碰的交互方式,将手机和全场景设备连接起来。然后通过手机端的原子化服务能力,快速完成配网、远程控制的能力,解决了应用与设备之间接续慢、…...

解决JQuery和其他库的冲突
文章目录 1.使用 noConflict() 方法:2.使用 IIFE(立即调用函数表达式):3.加载顺序:4.使用命名空间:5.使用 jQuery Migrate 插件: 1.使用 noConflict() 方法: 这是最常见和简单的解决…...

【Linux】在 Linux 上模拟网络故障
文章目录 模拟网络丢包模拟网络延迟、抖动模拟网络包重复模拟网络带宽受限模拟网络错误模拟网络乱序配合 cgroup 进行进程级带宽限制重置网络清空所有规则 模拟网络丢包 # 在eth0网络接口上替换排队规则,应用netem规则来模拟30%的数据包丢失 tc qdisc replace dev …...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
