头歌-机器学习 第16次实验 EM算法
第1关:极大似然估计
任务描述
本关任务:根据本节课所学知识完成本关所设置的选择题。
相关知识
为了完成本关任务,你需要掌握:
-
什么是极大似然估计;
-
极大似然估计的原理;
-
极大似然估计的计算方法。
什么是极大似然估计
没有接触过或者没有听过”极大似然估计“的同学可能会被这个名词唬住(每个字都认识,但是连起来就不知道是什么意思了),我们不妨拆字释意。
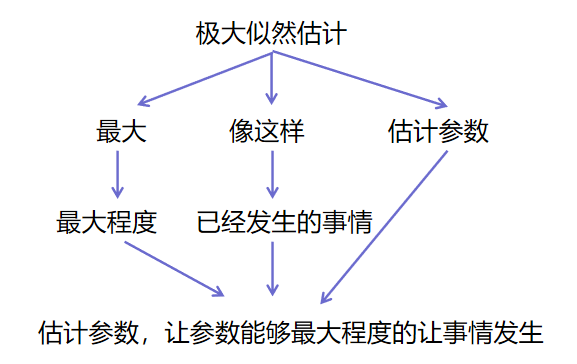
光看拆字释意后的解释可能还是有点绕。不如举个例子:一个袋子中总共有黑白两种颜色的球,总共有 100 个,其中一种颜色的球有 90 个。现在随机从袋子中取出一个球,发现是黑球。那么问你是黑色球有 90 个,还是白色球 90 个?
此时你可能会认为是黑色球有 90 个。因为随机抽取一个球,是黑色的(已经发生的事情),说明黑色抽中的概率最大(最大程度),因此猜测 90 个的是黑色球(估计)。这其实就是极大似然估计。
极大似然估计的原理
如果用数学语言来描述极大似然估计的话,就是如果事件的发生与参数heta有关,并假设事件发生时的样本为x1,...,xk,那么h^eta(x1,...,xk)就是参数heta的估计值。当heta=h^eta(x1,...,xk)时,表示当前样本发生的概率最大。
举个例子:在《权力的游戏》中有个场景,老徒利死的时候,尸体放在船上,需要弓箭手在岸边发射火箭引燃。但是当时的艾德慕·徒利公爵射了三箭都没中,布林登·徒利实在看不下去了,通过旗帜判断风向,一箭命中!因此箭能否射中靶心,不仅跟弓箭手的瞄准能力有关,还跟外界的风向有关系。假设不考虑人的因素,只考虑风的大小。同样的瞄准和力度,风太大不行、太小也不行。那我们如果给风的大小设置一个值为heta。假设一名弓箭手射出了三只箭,分别是8环、6环、7环(即x1=8,x2=6,x3=7),当时风的大小为88。那么我们认为只有heta=88,发生上面事件的概率最大。
极大似然估计的计算方法
假设一个袋子装有白球与红球,比例未知,现在抽取 10 次(每次抽完都放回,保证事件独立性),假设抽到了 7 次白球和 3 次红球,在此数据样本条件下,你可能会下意识的认为袋子中白球的比例为 0.7,但是我们同样可以采用最大似然估计法求解袋子中白球的比例。
假设袋子中白球的比例为参数heta。简单起见,首先定义从袋子中随机抽取两次球摸到白球和红球的概率,如下(其中f表示模型,x1表示第一次摸球,x2表示第二次摸球):
f(x1,x2∣heta)=f(x1∣heta)∗f(x2∣heta)
由于heta是未知的,所以我们将这个未知量heta放到一个函数中作为参数,这个函数称为似然函数。
L(heta∣x1,x2)=f(x1,x2∣heta)=prodi=12f(xi∣heta)
有了似然函数之后,很明显,就是想要知道当heta为何值时似然函数L得值最大。找到了这个heta就相当于完成了极大似然估计。那么怎么找呢?回忆一下高中所学的知识,会发现可以通过对heta求导。但是现在的似然函数L求导不方便,所以我们需要对似然函数L取对数处理。经过取对数处理后的似然函数通常称为对数似然函数。
lnL(heta∣x1,x2)=lnf(x1,x2∣heta)=sumi=12lnf(xi∣heta)
为了数学计算上更方便,通常会对对数似然函数求个均值,得到平均对数似然函数。
l^=21lnL(heta∣x1,x2)
若将找到的合适的heta表示为h^etamle,则有:
h^etamle=argmaxl^(heta∣x1,x2)
这是从袋子里随机抽取两个球的极大似然估计的数学表示。例子中是从袋子里随机抽取了十次球,根据刚刚所学的知识,我们能够很容易的进行扩展。假设抽取到白球的概率为heta,很显然抽取到红球的概率就是1−heta。所以从袋子里抽取十次,有七次是抽到白球的似然函数L可以表示为:
L(heta∣x1,x2,...,x10)=f(x1∣heta)∗f(x2∣heta)∗...∗f(x10∣heta)=heta7(1−heta)3
所以其平均对数似然函数可表示为:
hatl=101ln(heta7(1−heta)3)
接下来就可以对heta求导,并令导数为0。
l^=7heta6(1−heta)3−3heta7(1−heta)2=0=>heta=0.7
我们会发现通过极大似然估计法计算出的白球的比例与我们下意识的判断一致。
因此极大似然估计的计算步骤总共 4 步:
1.构造似然函数L(heta); 2.取对数lnL(heta); 3.求导,并让导数为0; 4.解方程得到heta。
编程要求
根据本关所学习到的知识,完成所有
相关文章:

头歌-机器学习 第16次实验 EM算法
第1关:极大似然估计 任务描述 本关任务:根据本节课所学知识完成本关所设置的选择题。 相关知识 为了完成本关任务,你需要掌握: 什么是极大似然估计; 极大似然估计的原理; 极大似然估计的计算方法。 什么是极大似然估计 没有接触过或者没有听过”极大似然估计“的同学…...

电脑启动引导的两种方式
电脑启动引导的两种方式 电脑启动引导有两种方式:Legacy 传统模式 和 UEFI 新型模式。 一、Legacy:指 主板的 传统的 BIOS 传输模式引导启动加载操作系统。 1.只支持 MBR 分区表,支持 32位和64位操作系统(如:winXP&…...

用php编写网站源码的一些经验
一、var_dump()函数 var_dump()函数在有页面跳转的情况下会看不到信息。因为 var_dump()函数输出信息默认显示到本页面。因此要看到var_dump()函数的输出,在有页面跳转时,需要将页面跳转改成显示本页面。 放在var_dump()函数里的变量如果是空值&#x…...
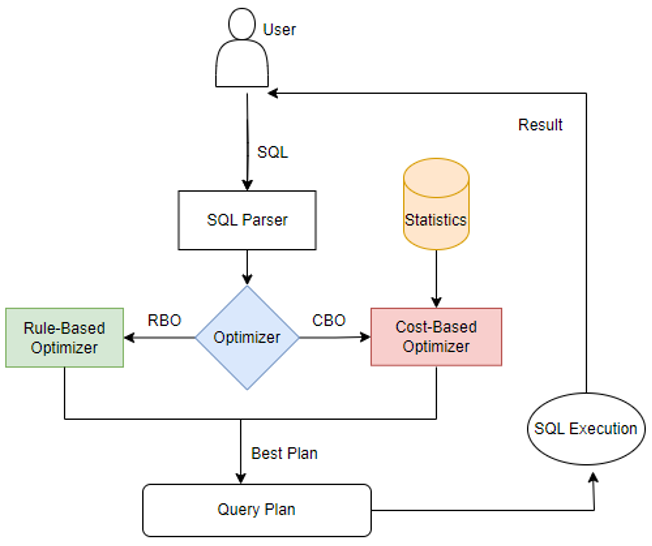
海山数据库(He3DB)原理剖析:浅析OLAP数据库计算引擎中的统计信息
背景: 统计信息在计算引擎的优化器模块中经常被提及,尤其是在基于成本成本优化(CBO)框架中统计信息发挥着至关重要的作用。CBO旨在通过评估执行查询的可能方法,并选择最有效的执行计划来提高查询性能。而统计信息则提…...
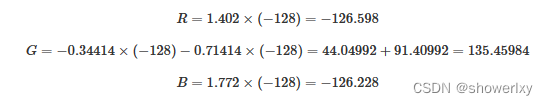
视频图像的两种表示方式YUV与RGB(4)
本篇主要讲YUV与RGB之间的转换,包括YUV444 颜色编码格式 转为 RGB 格式 ,RGB颜色编码格式转为 YUV444 格式。 一、 YUV与RGB之间的转换 YUV与RGB颜色格式之间进行转换时 , 涉及一系列的数学运算 ; YUV 颜色编码格式转为RGB格式的转换公式 取决于 于 YUV …...
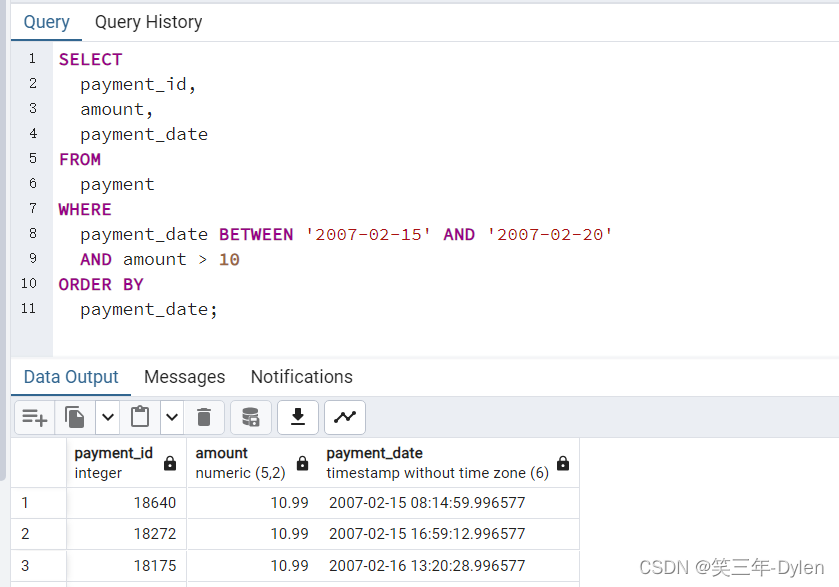
PostgreSQL入门到实战-第十四弹
PostgreSQL入门到实战 PostgreSQL数据过滤(七)官网地址PostgreSQL概述PostgreSQL中BETWEEN 命令理论PostgreSQL中BETWEEN 命令实战更新计划 PostgreSQL数据过滤(七) BETWEEN运算符允许您检查值是否在值的范围内。 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容…...

分布式数据库中间件 Mycat 和 ShardingSphere 对比
Mycat 和 ShardingSphere 都是流行的分布式数据库中间件,都可以用于实现数据分片、读写分离和分布式事务等功能,但它们在设计理念、特点和功能实现上有一些区别 1. 设计理念: Mycat: 基于 MySQL 协议的代理式架构,主要…...
Python实现BOA蝴蝶优化算法优化BP神经网络回归模型(BP神经网络回归算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 蝴蝶优化算法(butterfly optimization algorithm, BOA)是Arora 等人于2019年提出的一种元启发式智能算…...
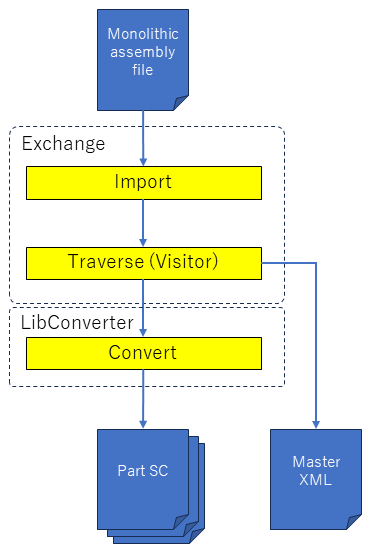
3D Web轻量化引擎HOOPS Commuicator如何从整体装配中创建破碎的装配零件和XML?
前言 虽然可以从某些本机CAD格式(其子组件驻留在单独的文件中,例如CATIA V5、Creo - Pro/E、NX或SolidWorks)创建破碎装配,但无法从整体装配文件(例如IFC、Revit)创建或3DXML。 本文介绍了一个示例&#…...
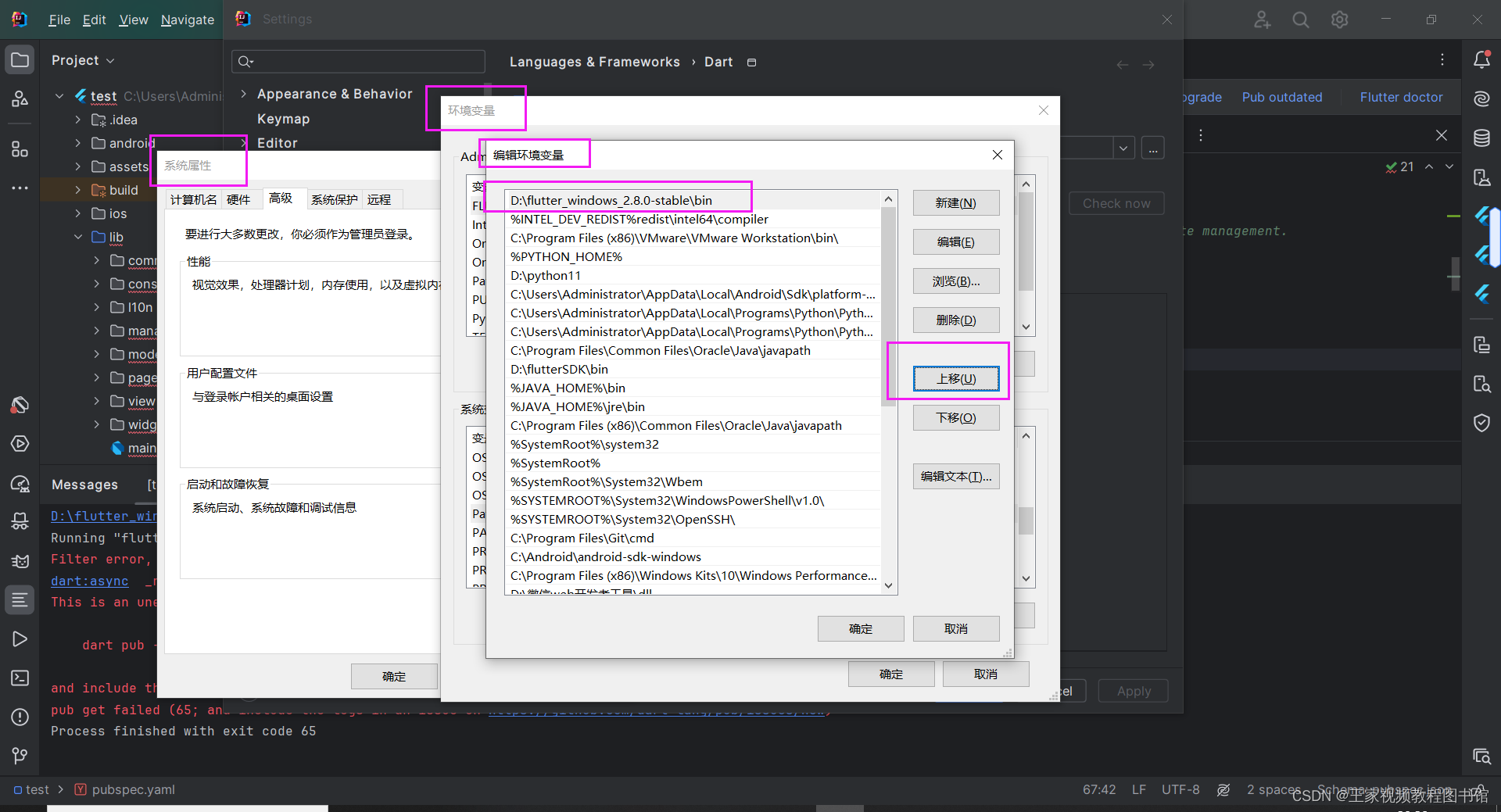
关于运行阿里云直播Demo pub get 报的错
flutter --version dart --version 如何使用Flutter框架推流_音视频终端 SDK(Apsara Video SDK)-阿里云帮助中心 终端输入 dart pub --trace get --no-precompile 打印详细报错信息 详细咨询chatgpt pub.dev 中已经是最新版本了 项目中已经是最新版本了 最终定位到 终端…...

C语言调用Python
目录 1.直接调用python语句 头文件引用 2.调用无参有参函数 1、调用无参函数 1.建立nopara.py文件 2.使用c语言根据上面流程进行调用 2、调用有参函数 1.建立nopara.py文件 2.使用c语言根据上面流程进行调用 C语言调用python需要我们已经安装好了libpython3的 dev依赖…...

SVN客户端异常问题处理
1、如遇svn服务端异常(所有用户登录不上) (1)登录192.168.**.**服务器,找到E:\仓库所在盘\VisualSVN-GlobalWinAuthz.ini (2)先备份VisualSVN-GlobalWinAuthz.ini文件 (3…...

gin+sse实现离散的消息通知
虽然网上的都是用sse实现将实时消息流不间断的推给前端,但是sse也可以模拟websocket进行突发的消息通知,而不是一直读取数据并返回数据。即服务端保存所有的连接对象,前端管理界面发送正常的http请求,在后端遍历所有的连接对象&am…...
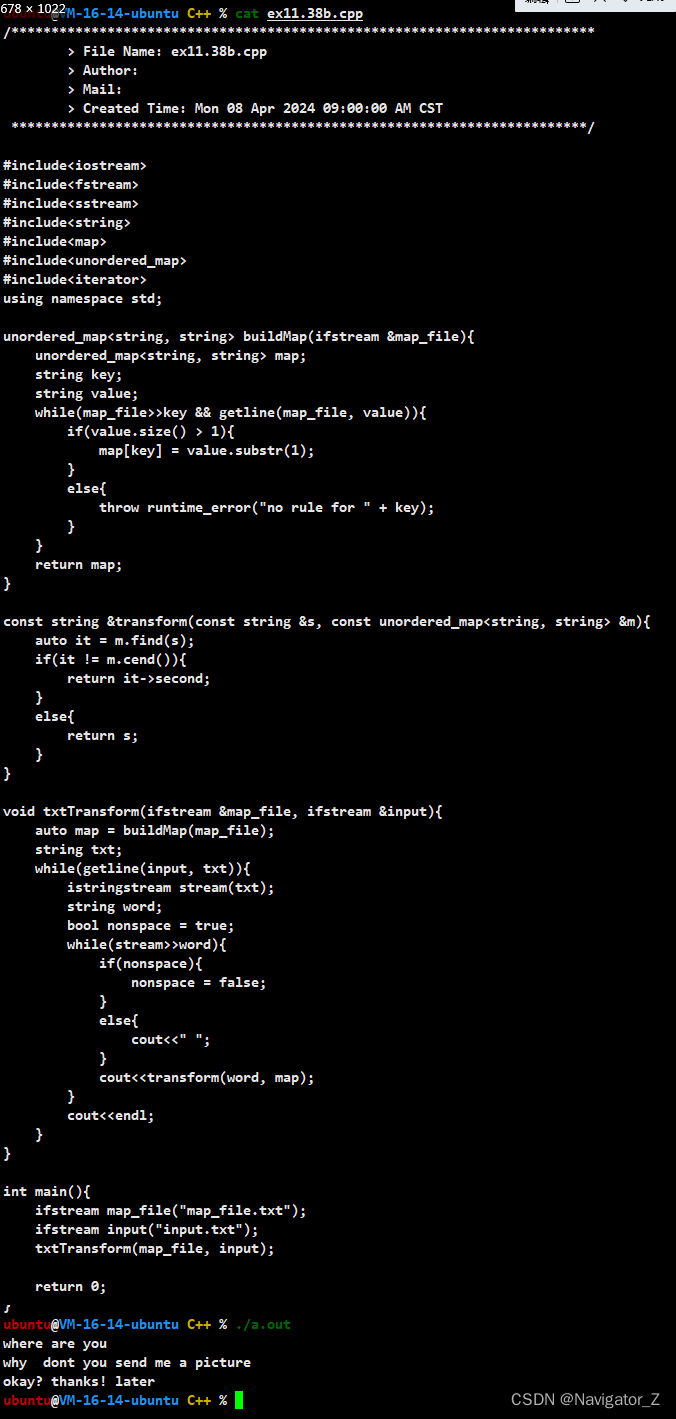
C++ //练习 11.38 用unordered_map重写单词计数程序(参见11.1节,第375页)和单词转换程序(参见11.3.6节,第391页)。
C Primer(第5版) 练习 11.38 练习 11.38 用unordered_map重写单词计数程序(参见11.1节,第375页)和单词转换程序(参见11.3.6节,第391页)。 环境:Linux Ubuntu࿰…...

【示例】MySQL-4类SQL语言-DDL-DML-DQL-DCL
前言 本文主要讲述MySQL中4中SQL语言的使用及各自特点。 SQL语言总共分四类:DDL、DML、DQL、DCL。 SQL-DDL | Data Definition Language 数据定义语言:用来定义/更改数据库对象(数据库、表、字段) 用途 | 操作数据库 # 查询所…...

基于SpringBoot+Vue的果蔬种植销售一体化服务平台(源码+文档+部署+讲解)
一.系统概述 伴随着我国社会的发展,人民生活质量日益提高。于是对果蔬种植销售一体化服务管理进行规范而严格是十分有必要的,所以许许多多的信息管理系统应运而生。此时单靠人力应对这些事务就显得有些力不从心了。所以本论文将设计一套果蔬种植销售一体…...

数据结构面试
当然可以!以下是数据结构面试问题及答案整理: **什么是数据结构?** 答:数据结构是指组织和存储数据的方式,它允许高效地访问和操作数据。不同的数据结构有不同的优势和适用场景。常见的基本数据结构包括数组、链表、…...

Linux 上安装 SQLite
SQLite Download Page 从上面的链接中源代码区下载 sqlite-autoconf-*.tar.gz。 历史版本见下连接: https://sqlite.org/chronology.html...
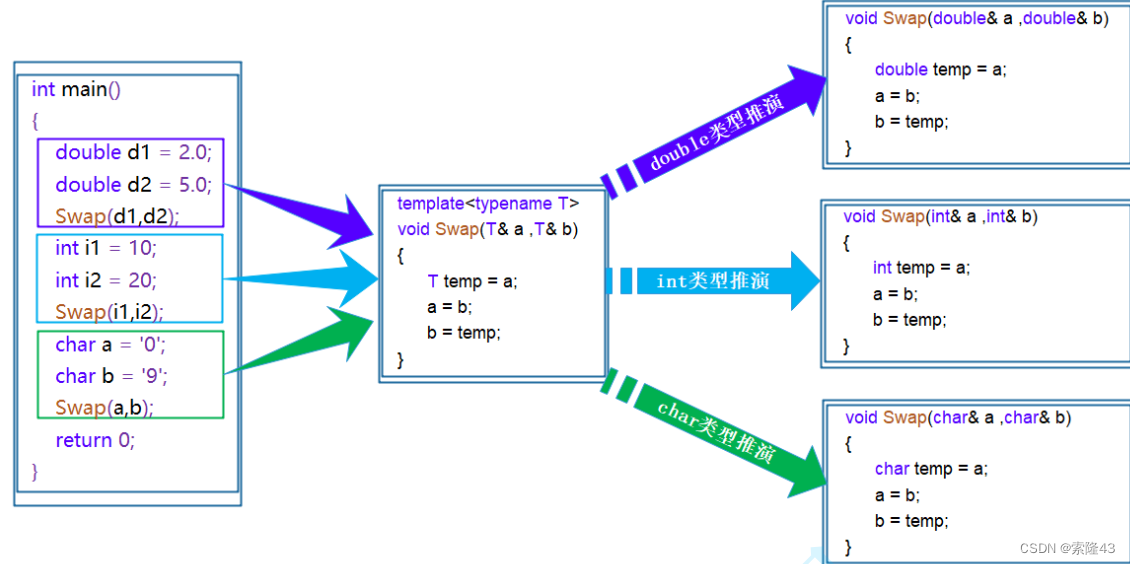
C++模板初阶(个人笔记)
模板初阶 1.泛型编程2.函数模板2.1函数模板的实例化2.2模板参数的匹配规则 3.类模板3.1类模板的实例化 1.泛型编程 泛型编程:编写与类型无关的通用代码,是代码复用的一种手段。模板是泛型编程的基础。 //函数重载 //交换函数的逻辑是一致的,…...

如何用Java后端处理JS.XHR请求
Touching searching engine destroies dream to utilize php in tomcat vector.The brave isn’t knocked down,turn its path to java back-end. Java Servlet Bible schematic of interaction between JS front-end and Java back-end Question 如何利用Java…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
