【数据结构】哈希
文章目录
- 1. 哈希概念
- 2. 哈希冲突
- 3. 哈希函数
- 4. 哈希冲突解决
- 4.1 闭散列
- 4.2 开散列

unordered 系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。
1. 哈希概念
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为 O(N),平衡树中为树的高度,即 O( l o g 2 N log_2 N log2N),搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。
如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
当向该结构中:
-
插入元素
根据待插入元素的关键码,以此函数计算出该元素的存储位置,并按此位置进行存放;
-
搜索元素
对元素的关键码进行同样的计算,把求得的函数值当作元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功。
该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(Hash Table)(或者散列表)。
例如:数据集合 { 1, 7, 6, 4, 5, 9 };
哈希函数设置为:hash(key) = key % capacity; capacity 为存储元素底层空间总的大小。

用该方法进行搜索不必进行多次关键码的比较,因此搜索的速度比较快。
问题:按照上述哈希方式,向集合中插入元素 44,会出现什么问题?
2. 哈希冲突
对于两个数据元素的关键字 k i k_i ki 和 k j k_j kj(i != j),有 k i k_i ki != k j k_j kj,但有:Hash( k i k_i ki) == Hash( k j k_j kj),即:不同关键字通过相同哈希函数计算出相同的哈希地址,这种现象称为哈希冲突或哈希碰撞。
把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
发生哈希冲突该如何处理呢?
3. 哈希函数
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。
哈希函数设计原则:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有 m 个地址时,其值域必须在 0 到 m - 1 之间;
- 哈希函数计算出来的地址能均匀分布在整个空间中;
- 哈希函数应该比较简单。
常见哈希函数:
-
直接定址法(常用)
取关键字的某个线性函数为散列地址:
Hash (Key) = A * Key + B;
优点:简单、均匀
缺点:需要事先知道关键字的分布情况;
使用场景:适合查找比较小且连续的情况。 -
除留余数法(常用)
设散列表中允许的地址数为 m,取一个不大于 m,但最接近或者等于 m 的质数 p 作为除数,按照哈希函数:
Hash (Key) = Key % p (p <= m),将关键码转换成哈希地址。 -
平方取中法(了解)
假设关键字为 1234,对它平方就是 1522756,抽取中间的 3 位 227 作为哈希地址;
再比如关键字为 4321,对它平方就是 18671041,抽取中间的 3 位 671(或 710)作为哈希地址;
平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况。 -
折叠法(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按照散列表表长,取后几位作为散列地址;
折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况。 -
随机数法(了解)
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即
Hash (Key) = random(Key),其中 random 为随机数函数;
通常应用于关键字长度不等时采用此法。 -
数学分析法(了解)
设有 n 个 d 位数,每一位可能有 r 种不同的符号,这 r 种不同的符号在各位上出现的频率不一定相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀,只有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。例如:

假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前 7 位都是相同的,那么我们可以选择后面的四位作为散列地址,如果这样的抽取工作还容易出现冲突,还可以对抽取出来的数字进行反转(如 1234 改成 4321)、右环移位(如 1234 改成 4123)、左环移位、前两数与后两数叠加(如 1234 改成 12+34=46)等方法;
数字分析法通常适合处理关键字位数比较多的情况。
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突。
4. 哈希冲突解决
解决哈希冲突两种常见的方法是:闭散列和开散列。
4.1 闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明哈希表中必然还有空位置,那么可以把 key 存放到冲突位置中的“下一个”空位置中去。那如何寻找下一个空位置呢?
-
线性探测
比如上面的场景:

现在需要插入元素 44,先通过哈希函数计算哈希地址,hashAddr 为 4,因此 44 理论上应该插在该位置,但是该位置已经放了值为 4 的元素,即发生哈希冲突。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
-
插入
-
通过哈希函数获取待插入元素在哈希表中的位置;
-
如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素。

-
-
删除
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他元素的搜索。比如删除元素 4,如果直接删除掉,44 查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。
// 哈希表每个空间给个标记 // EMPTY此位置空, EXIST此位置已经有元素, DELETE元素已经删除 enum State {EMPTY,EXIST,DELETE };
-
-
线性探测的实现
// 注意:假如实现的哈希表中元素唯一,即key相同的元素不再进行插入 // 为了实现简单,此哈希表中我们将比较直接与元素绑定在一起 template<class K, class V> class HashTable {struct Elem{pair<K, V> _val;State _state;};public:HashTable(size_t capacity = 3): _ht(capacity), _size(0){for (size_t i = 0; i < capacity; ++i)_ht[i]._state = EMPTY;}bool Insert(const pair<K, V>& val){// 检测哈希表底层空间是否充足// _CheckCapacity();size_t hashAddr = HashFunc(key);// size_t startAddr = hashAddr;while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first == key)return false;hashAddr++;if (hashAddr == _ht.capacity())hashAddr = 0;/*转一圈也没有找到,注意:动态哈希表,该种情况可以不用考虑,哈希表中元素个数到达一定的数量,哈希冲突概率会增大,需要扩容来降低哈希冲突,因此哈希表中元素是不会存满的if(hashAddr == startAddr)return false;*/}// 插入元素_ht[hashAddr]._state = EXIST;_ht[hashAddr]._val = val;_size++;return true;}int Find(const K& key){size_t hashAddr = HashFunc(key);while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first == key)return hashAddr;hashAddr++;}return hashAddr;}bool Erase(const K & key){int index = Find(key);if (-1 != index){_ht[index]._state = DELETE;_size++;return true;}return false;}size_t Size()const;bool Empty() const;void Swap(HashTable<K, V, HF>& ht);private:size_t HashFunc(const K& key){return key % _ht.capacity();}private:vector<Elem> _ht;size_t _size; };思考:哈希表什么情况下进行扩容?如何扩容?

void CheckCapacity() {if (_size * 10 / _ht.capacity() >= 7){HashTable<K, V, HF> newHt(GetNextPrime(ht.capacity));for (size_t i = 0; i < _ht.capacity(); ++i){if (_ht[i]._state == EXIST)newHt.Insert(_ht[i]._val);}Swap(newHt);} }线性探测优点:实现非常简单;
线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要多次比较,导致搜索效率降低,如何缓解?
-
二次探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为: H i H_i Hi = ( H 0 H_0 H0 + i 2 i^2 i2 ) % m。其中:i = 1, 2, 3…, H 0 H_0 H0 是通过散列函数 Hash(x) 对关键码 key 进行计算得到的位置,m 是表的大小。
对于上面案例,如果要插入 44,产生冲突,使用二次探测解决后的情况为:

研究表明:当表的长度为质数且表装载因子 a 不超过 0.5 时,新的表项一定能够插入。而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子 a 不超过 0.5,如果超出必须考虑增容。
因此:闭散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷。
4.2 开散列
-
开散列的概念
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头节点存储在哈希表中。
个人理解:哈希桶 = 顺序表 + 链表 + 哈希算法;


从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
-
开散列实现
template<class V> struct HashBucketNode {HashBucketNode(const V& data): _pNext(nullptr), _data(data){}HashBucketNode<V>* _pNext;V _data; };// 本文所实现的哈希桶中key是唯一的 template<class V> class HashBucket {typedef HashBucketNode<V> Node;typedef Node* PNode; public:HashBucket(size_t capacity = 3) : _size(0){_ht.resize(GetNextPrime(capacity), nullptr);}// 哈希桶中的元素不能重复PNode* Insert(const V& data){// 确认是否需要扩容。。。// _CheckCapacity();// 1. 计算元素所在的桶号size_t bucketNo = HashFunc(data);// 2. 检测该元素是否在桶中PNode pCur = _ht[bucketNo];while (pCur){if (pCur->_data == data)return pCur;pCur = pCur->_pNext;}// 3. 插入新元素pCur = new Node(data);pCur->_pNext = _ht[bucketNo];_ht[bucketNo] = pCur;_size++;return pCur;}// 删除哈希桶中为data的元素(data不会重复),返回删除元素的下一个节点PNode* Erase(const V& data){size_t bucketNo = HashFunc(data);PNode pCur = _ht[bucketNo];PNode pPrev = nullptr, pRet = nullptr;while (pCur){if (pCur->_data == data){if (pCur == _ht[bucketNo])_ht[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;pRet = pCur->_pNext;delete pCur;_size--;return pRet;}}return nullptr;}PNode* Find(const V& data);size_t Size()const;bool Empty()const;void Clear();bool BucketCount()const;void Swap(HashBucket<V, HF>& ht;~HashBucket();private:size_t HashFunc(const V& data){return data % _ht.capacity();}private:vector<PNode*> _ht;size_t _size; // 哈希表中有效元素的个数 }; -
开散列增容
桶的个数是一定的,随着元素的不断插入。每个桶中元素的个数不断增多,极端情况下,可能会导致一个桶中链表节点非常多,会影响哈希表的性能,因此在一定条件下需要对哈希表进行增容,那该条件怎么确认呢?开散列最好的情况是:每个哈希桶中刚好挂一个节点,再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可以给哈希表增容。
void _CheckCapacity(){size_t bucketCount = BucketCount();if (_size == bucketCount){HashBucket<V, HF> newHt(bucketCount);for (size_t bucketIdx = 0; bucketIdx < bucketCount; ++bucketIdx){PNode pCur = _ht[bucketIdx];while (pCur){// 将该节点从原哈希表中拆出来_ht[bucketIdx] = pCur->_pNext;// 将该节点插入到新哈希表中size_t bucketNo = newHt.HashFunc(pCur->_data);pCur->_pNext = newHt._ht[bucketNo];newHt._ht[bucketNo] = pCur;pCur = _ht[bucketIdx];}}newHt._size = _size;this->Swap(newHt);}} -
开散列的思考
-
只能存储 key 为整型的元素,其他类型怎么解决?
// 哈希函数采用除留余数法,被模的key必须要为整形才可以处理,此处提供将key转化为整形的方法 // 整形数据不需要转化 template<class T> class DefHashF { public:size_t operator()(const T& val){return val;} };// key为字符串类型,需要将其转化为整形 class Str2Int { public:size_t operator()(const string& s){const char* str = s.c_str();unsigned int seed = 131; // 31 131 1313 13131 131313unsigned int hash = 0;while (*str){hash = hash * seed + (*str++);}return (hash & 0x7FFFFFFF);} };// 为了实现简单,此哈希表中我们将比较直接与元素绑定在一起 template<class V, class HF> class HashBucket {// …… private:size_t HashFunc(const V& data){return HF()(data.first) % _ht.capacity();} }; -
除留余数法,最好模一个素数,如何每次快速取一个类似两倍关系的素数?
size_t GetNextPrime(size_t prime) {const int PRIMECOUNT = 28;static const size_t primeList[PRIMECOUNT] ={53ul, 97ul, 193ul, 389ul, 769ul,1543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul, 98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul,25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul,805306457ul,1610612741ul, 3221225473ul, 4294967291ul};size_t i = 0;for (; i < PRIMECOUNT; ++i){if (primeList[i] > prime)return primeList[i];}return primeList[i]; }
-
-
开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销。事实上:由于开地址法必须保持大量的空闲空间以确保搜索效率,如二次探测法要求装载因子 a <= 0.7,而表项所占空间又比指针大得多,所以使用链地址法反而比开地址法节省存储空间。
相关文章:

【数据结构】哈希
文章目录 1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决4.1 闭散列4.2 开散列 unordered 系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。 1. 哈希概念 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系ÿ…...

Kubernetes(k8s)监控与报警(qq邮箱+钉钉):Prometheus + Grafana + Alertmanager(超详细)
Kubernetes(k8s)监控与报警(qq邮箱钉钉):Prometheus Grafana Alertmanager(超详细) 1、部署环境2、基本概念简介2.1、Prometheus简介2.2、Grafana简介2.3、Alertmanager简介2.4、Prometheus …...
STM32-04基于HAL库(CubeMX+MDK+Proteus)中断案例(按键中断扫描)
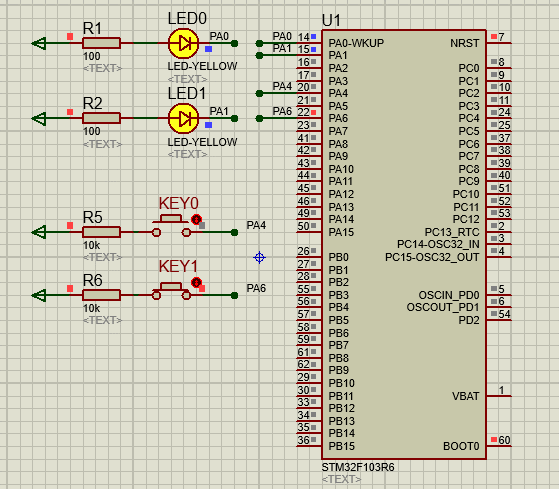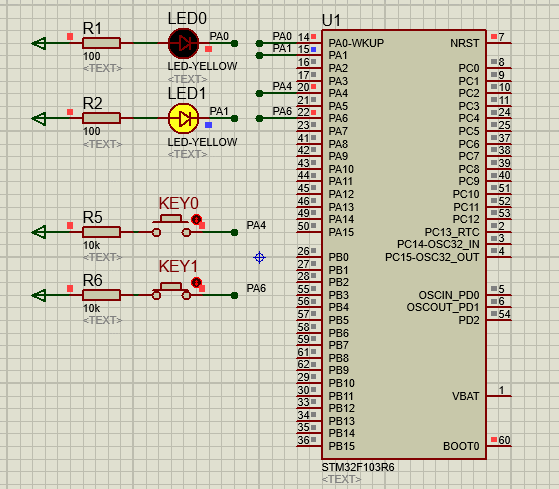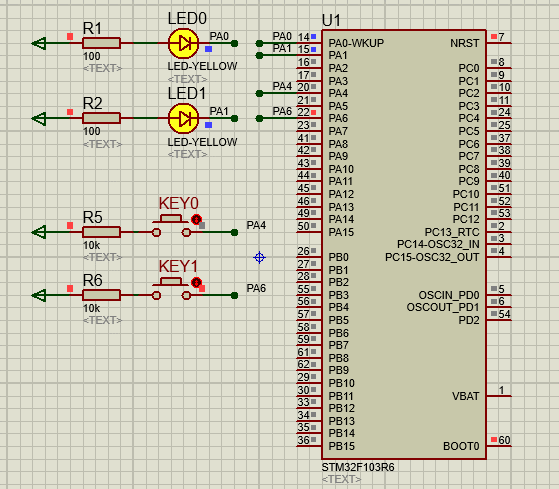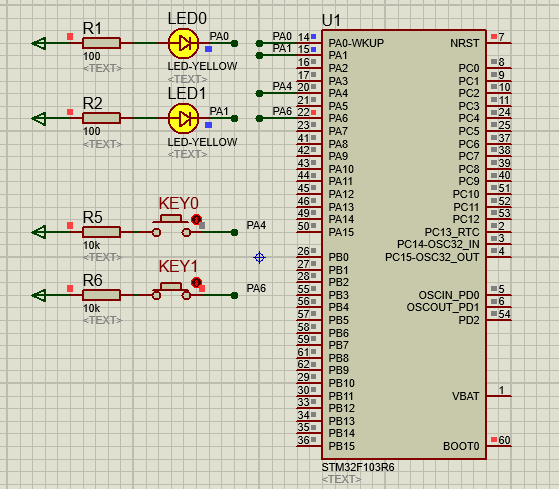
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式,生成代码四、MDK打开生成项目,编写HAL库的按键检测代码五、运行仿真程序,调试代码 一、功能需求分析 在完成GPIO输入输出案例之后,开始新的功能…...
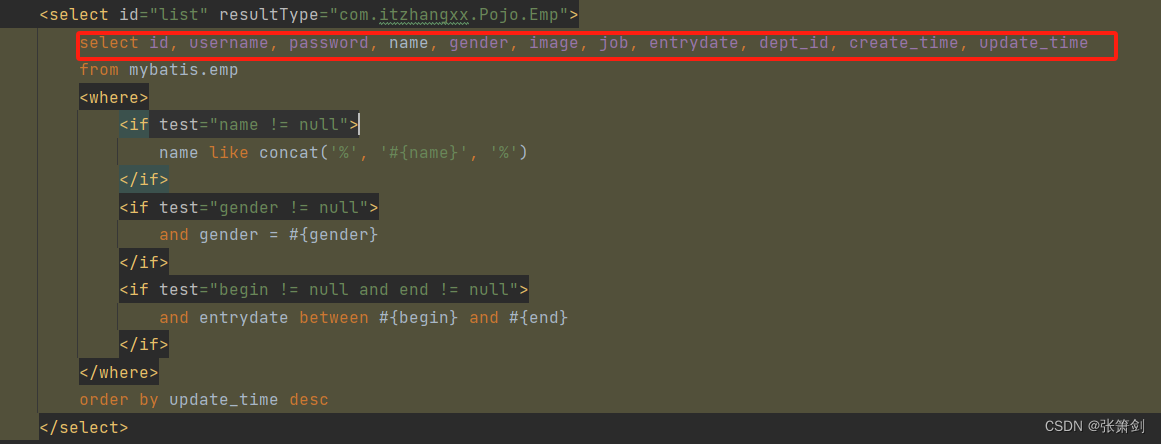
第十五篇:Mybatis
文章目录 一、什么是MyBatis二、Mybatis入门案例三、配置SQL提示四、数据库连接池四、lombok五、mybatis基础操作5.1 根据id删除5.2 预编译SQL5.3 新增员工5.4 更新员工5.5 查询员工(用于页面回显)5.6 条件查询 七、XML映射文件八、动态SQL8.1 if语句8.2…...
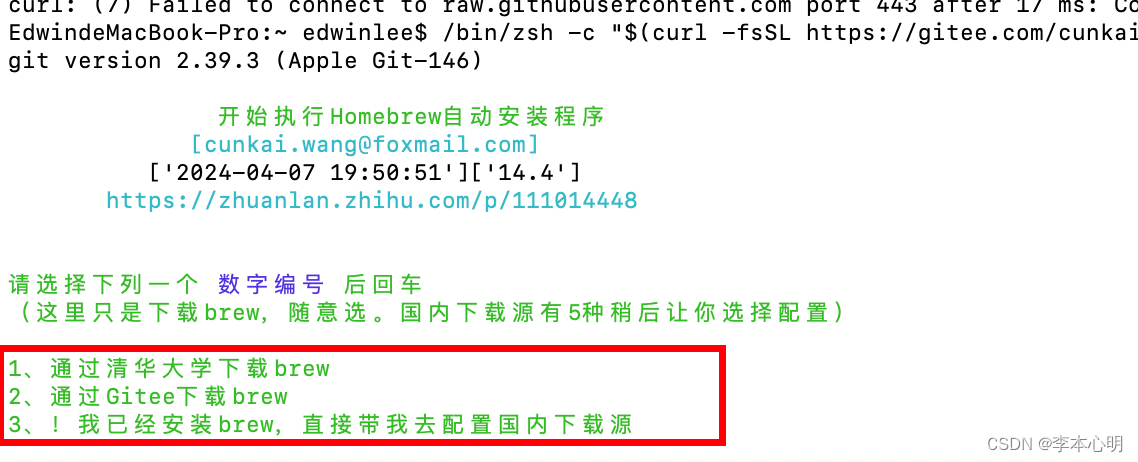
【MacBook系统homebrew镜像记录】
安装 使用Homebrew 国内源安装脚本,贼方便: /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"切换至清华大学镜像源: 命令合并: 分别切换了 brew.git、 homebrew-core.git、 homebrew-…...

深拷贝总结
JSON.parse(JSON.stringify(obj)) 这行代码的运行过程,就是利用 JSON.stringify 将js对象序列化(JSON字符串),再使用JSON.parse来反序列化(还原)js对象;序列化的作用是存储和传输。(…...

RabbitMQ在云原生环境中部署和应用实践
一、RabbitMQ和云原生技术的关系 RabbitMQ是一种开源的、实现了先进的消息队列协议(AMQP)的消息队列软件。而云原生技术就是为在公共云、私有云以及其他各种云环境提供应用的一种方法。RabbitMQ和云原生技术在分布式系统和微服务架构中都起到了关键作用…...
和上传至服务器)
flask 后端 + 微信小程序和网页两种前端:调用硬件(相机和录音)和上传至服务器
选择 flask 作为后端,因为后续还需要深度学习模型,python 语言最适配;而 flask 框架轻、学习成本低,所以选 flask 作为后端框架。 微信小程序封装了调用手机硬件的 api,通过它来调用手机的摄像头、录音机,…...
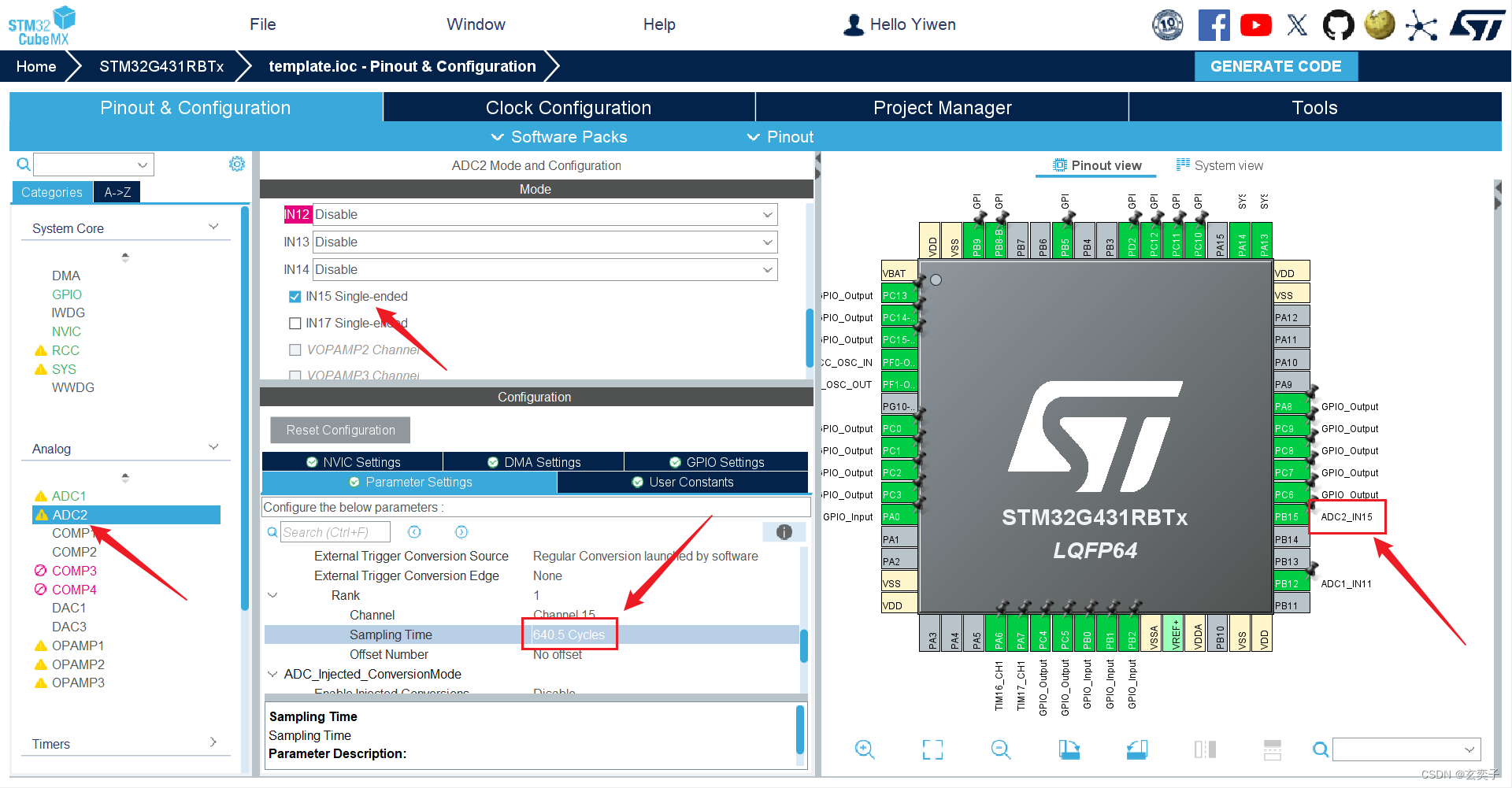
蓝桥杯嵌入式(G431)备赛笔记——ADC+LCD
目录 题目要求(真题): cubeMX配置: 小试牛刀: Keil代码: 效果演示: 题目要求(真题): 使用第十一届第二场真题,练习ADC波部分的代码 cubeMX配…...
)
最近公共祖先(LCA)
题目描述 如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。 输入格式 第一行包含三个正整数 N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。 接下来 N−1 行每行包含两个正整数x,y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以…...

ABBYY FineReader15免费电脑OCR图片文字识别软件
产品介绍:ABBYY FineReader 15 OCR图片文字识别软件 ABBYY FineReader 15是一款光学字符识别(OCR)软件,专门设计用于将扫描的文档、图像和照片中的文本转换成可编辑和可搜索的格式。这款软件利用先进的OCR技术,能够识别…...

2024年第十七届 认证杯 网络挑战赛 (A题)| 保暖纤维的保暖能力 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 让我们来看看认证杯 网络挑战赛 (A题)!…...

算法训练营第37天|LeetCode 738.单调递增的数字 968.监控二叉树
LeetCode 738.单调递增的数字 题目链接: LeetCode 738.单调递增的数字 解题思路: 从后向前遍历,当不满足递增条件时,当前位置赋值为9,前一位减一。之后记录不满足位置,将后续全部赋值为9. 代码&#x…...
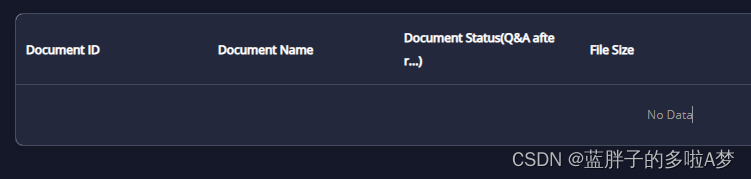
Vue+el-table 修改表格 单元格横线边框颜色及表格空数据时边框颜色
需求 目前 找到对应的css样式进行修改 修改后 css样式 >>>.el-table th.el-table__cell.is-leaf {border-bottom: 1px solid #444B5F !important;}>>>.el-table td.el-table__cell,.el-table th.el-table__cell.is-leaf {border-bottom: 1px solid #444B5F …...

大恒相机-程序异常退出后显示被占用
心跳时间代表多久向相机发送一次心跳包,如果超时则设备会认为断开了,停止工作并主动释放占用资源。 在相机打开后添加代码: #ifdef _DEBUG//设置心跳超时时间 3sObjFeatureControlPtr->GetIntFeature("GevHeartbeatTimeout")-&…...
头歌-机器学习 第16次实验 EM算法
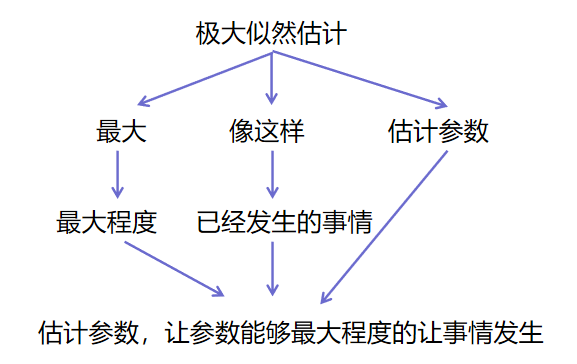
第1关:极大似然估计 任务描述 本关任务:根据本节课所学知识完成本关所设置的选择题。 相关知识 为了完成本关任务,你需要掌握: 什么是极大似然估计; 极大似然估计的原理; 极大似然估计的计算方法。 什么是极大似然估计 没有接触过或者没有听过”极大似然估计“的同学…...

电脑启动引导的两种方式
电脑启动引导的两种方式 电脑启动引导有两种方式:Legacy 传统模式 和 UEFI 新型模式。 一、Legacy:指 主板的 传统的 BIOS 传输模式引导启动加载操作系统。 1.只支持 MBR 分区表,支持 32位和64位操作系统(如:winXP&…...

用php编写网站源码的一些经验
一、var_dump()函数 var_dump()函数在有页面跳转的情况下会看不到信息。因为 var_dump()函数输出信息默认显示到本页面。因此要看到var_dump()函数的输出,在有页面跳转时,需要将页面跳转改成显示本页面。 放在var_dump()函数里的变量如果是空值&#x…...
海山数据库(He3DB)原理剖析:浅析OLAP数据库计算引擎中的统计信息
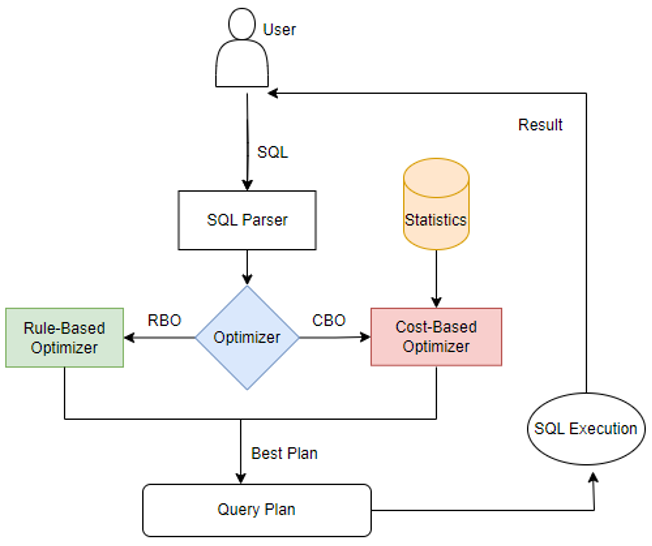
背景: 统计信息在计算引擎的优化器模块中经常被提及,尤其是在基于成本成本优化(CBO)框架中统计信息发挥着至关重要的作用。CBO旨在通过评估执行查询的可能方法,并选择最有效的执行计划来提高查询性能。而统计信息则提…...
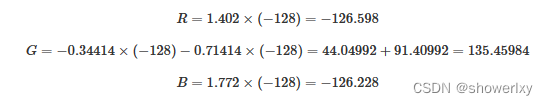
视频图像的两种表示方式YUV与RGB(4)
本篇主要讲YUV与RGB之间的转换,包括YUV444 颜色编码格式 转为 RGB 格式 ,RGB颜色编码格式转为 YUV444 格式。 一、 YUV与RGB之间的转换 YUV与RGB颜色格式之间进行转换时 , 涉及一系列的数学运算 ; YUV 颜色编码格式转为RGB格式的转换公式 取决于 于 YUV …...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
