快速排序:深入解析其原理、实现与性能特性
快速排序,以其名字所示,是一种追求速度的高效排序算法。作为分治法在排序问题上的典型应用,快速排序凭借其平均情况下近乎理想的O(n log n)时间复杂度和简洁的实现逻辑,在实际编程与数据处理中占据着重要地位。本篇博客将详细解析快速排序的原理、实现步骤,探讨其性能特性,并概述其在不同场景下的适用性。
一、快速排序原理
快速排序的基本思想是分而治之与递归。它通过一趟排序将待排序序列划分为两个部分,使得其中一部分的所有元素都比另一部分的所有元素要小,然后再分别对这两部分继续进行快速排序,整个过程递归进行,直到序列中的元素只剩下一个,即达到完全有序的状态。
这个划分过程的关键在于选取一个基准元素(pivot),并围绕它进行分区操作。分区操作确保基准元素最终会处于其最终排序位置上,同时将小于基准的元素置于其左侧,大于基准的元素置于其右侧。这样的分区操作实现了序列的“相对有序”,为后续递归排序奠定了基础。
二、快速排序实现步骤
以下是快速排序的具体实现步骤:
1. 选择基准元素 从待排序序列中选择一个元素作为基准。常见的选择方法有随机选取、首元素、中位数法等。
2. 分区操作 从待排序序列两端开始,分别向中间扫描。左指针找到大于基准的元素,右指针找到小于基准的元素。当左指针小于右指针时,交换这两个元素的位置。如此反复,直到左指针与右指针相遇。此时,将基准元素与左指针所在位置的元素交换,完成分区。
3. 递归排序 对基准元素左边和右边的子序列分别进行快速排序,直至子序列长度为1(已经有序)。
以下是快速排序算法的代码:
Python
def quick_sort(arr): if len(arr) <= 1: return arr pivot = arr[len(arr) // 2] # 选择中间元素作为基准值 left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quick_sort(left) + middle + quick_sort(right) # 示例
arr = [3,6,8,10,1,2,1]
print("原始数组:", arr)
sorted_arr = quick_sort(arr)
print("快速排序后的数组:", sorted_arr)def partition(arr, low, high): i = low - 1 # 指向小于基准值的最后一个元素的索引 pivot = arr[high] # 选择最右边的元素作为基准值 for j in range(low, high): # 如果当前元素小于或等于基准值 if arr[j] <= pivot: i = i + 1 # 增加小于基准值的元素的计数 arr[i], arr[j] = arr[j], arr[i] # 交换元素 arr[i + 1], arr[high] = arr[high], arr[i + 1] # 将基准值放到正确的位置 return i + 1 def quick_sort_inplace(arr, low, high): if low < high: # pi 是分区索引,arr[pi] 现在在正确的位置 pi = partition(arr, low, high) # 递归地对左半部分和右半部分进行排序 quick_sort_inplace(arr, low, pi - 1) quick_sort_inplace(arr, pi + 1, high) # 示例
arr = [3,6,8,10,1,2,1]
n = len(arr)
quick_sort_inplace(arr, 0, n - 1)
print("快速排序后的数组:", arr)三、快速排序的时间复杂度与空间复杂度
时间复杂度: 在最理想的情况下,每次分区都能均匀划分,快速排序的时间复杂度为O(n log n)。在最坏情况下(输入序列已经完全有序或逆序),每次只能将序列划分为一个元素和剩余元素两部分,时间复杂度退化为O(n²)。然而,通过合理的基准选择策略(如随机选取),实际应用中快速排序的平均时间复杂度接近最佳情况。
空间复杂度: 快速排序的递归实现需要栈空间存储递归调用的信息。在最坏情况下,递归深度为n,空间复杂度为O(n)。但通过采用尾递归优化或迭代实现,可将空间复杂度降至O(log n)。
四、快速排序的特点与优缺点
特点:
- 不稳定性:快速排序是一种不稳定的排序算法,即相等元素的相对顺序在排序过程中可能会改变。
- 原地排序:通过合理实现,快速排序可以做到在原地进行排序,无需额外存储空间。
优点:
- 效率高:平均时间复杂度为O(n log n),在处理大规模数据时表现出色。
- 原地排序:对内存资源需求较低,尤其适合内存受限的场景。
缺点:
- 最坏情况性能差:当输入序列极度有序时,性能退化至O(n²)。但可通过随机化选择基准元素来避免这种情况。
- 不稳定:对于需要保持相等元素相对顺序的场景,快速排序可能不适用。
五、快速排序的应用场景
1. 大规模数据排序 快速排序在处理大规模数据时,其平均时间复杂度为O(n log n),在实践中往往能提供高效排序能力,常用于数据库、数据分析等领域。
2. 内存敏感场景 快速排序的原地排序特性使其在内存资源有限或对内存消耗敏感的环境中具有优势。
3. 随机性较强的输入 当输入数据的分布较为随机时,快速排序的性能更接近其平均情况,表现优异。
综上所述,快速排序凭借其高效的平均时间复杂度、简洁的实现逻辑以及原地排序的特性,在众多实际应用中展现出强大的竞争力。虽然在特定场景下存在稳定性问题和最坏情况性能退化的风险,但通过合理选择基准元素和优化实现,快速排序仍不失为一种广泛应用的高效排序算法。理解并掌握快速排序,无疑将提升您在数据处理任务中的算法实践能力。
相关文章:

快速排序:深入解析其原理、实现与性能特性
快速排序,以其名字所示,是一种追求速度的高效排序算法。作为分治法在排序问题上的典型应用,快速排序凭借其平均情况下近乎理想的O(n log n)时间复杂度和简洁的实现逻辑,在实际编程与数据处理中占据着重要地位。本篇博客将详细解析…...
一文看懂Mac地址
一、Mac地址是什么? 虽然IP地址已经成为一个家喻户晓的术语,但还有一个同样重要的数字标识符值得我们关注——MAC地址。在本文中,我们旨在阐明网络中这个经常被忽视的方面。加入我们,深入研究 MAC 地址的世界,了解它们…...

2024.4.10作业
#include "widget.h" #include "ui_widget.h" Widget::Widget(QWidget *parent) : QWidget(parent) , ui(new Ui::Widget) { ui->setupUi(this); } Widget::~Widget() { delete ui; } //显示时间 void Widget::timerEvent(QTimerEvent *e) { QT…...

python - Django创建项目
项目运行命令 根目录下运行命令: python manage.py runserver win环境创建项目 直接使用 Pycharm 创建项目 在 cmd 或 Linux 命令行环境下创建 Django 项目 django-admin startproject mysite 这样就会在当前目录下创建一个叫做 mysite 的Django项目。 可以看到Djang…...

WPF —— 动画缩放变换
ScaleTransform:在二维x-y坐标系统内缩放对象; 在故事板中依赖的属性为RenderTransform.ScaleX或RenderTransform.ScaleY,这要根据你要沿哪个轴进行缩放,X代表x轴,Y代表y轴; key属性当我们使用静态资源访问时候--> <!--TargetType"{x:Type Button} 直接应用…...
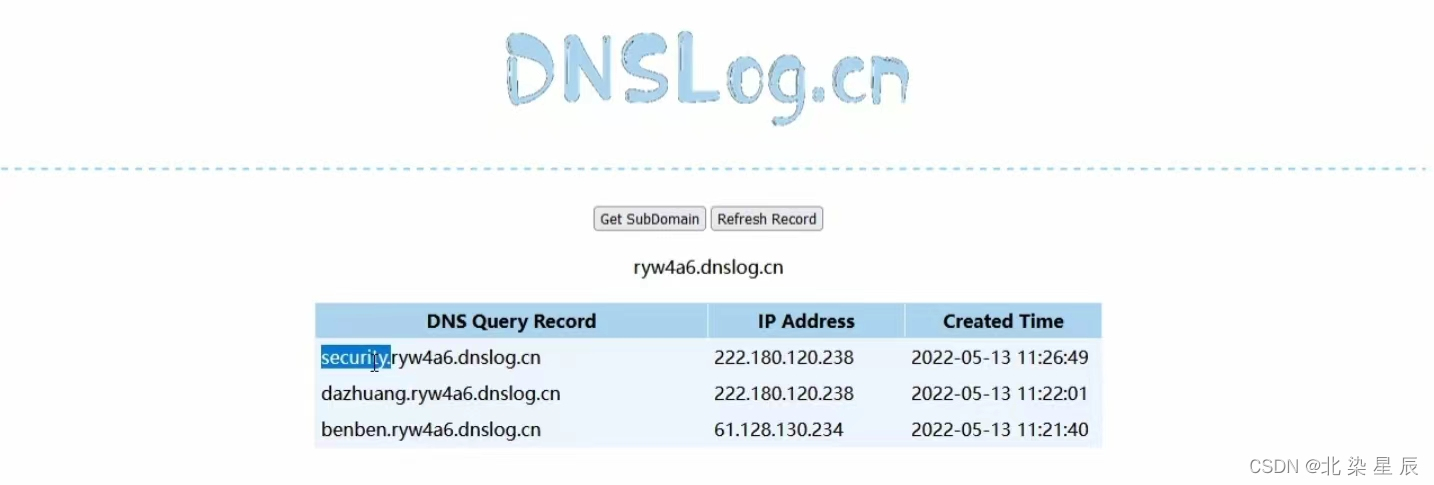
SQL注入---盲注
文章目录 目录 一.盲注概述 布尔盲注: 时间盲注: 一.盲注概述 注是一种SQL注入攻击的形式,在这种攻击中,攻击者向目标应用程序发送恶意注入代码,然后通过观察应用程序的响应来推断出数据库中的信息。与常规的SQL注入…...
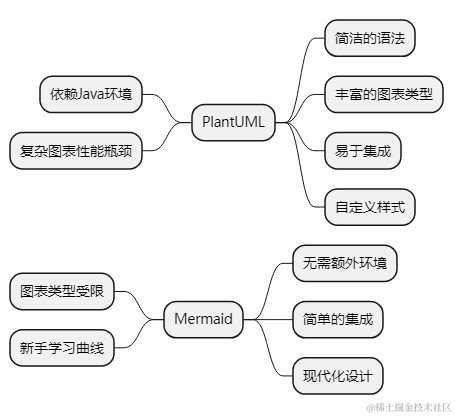
PlanUML和Mermaid哪个好?
引言 在当今信息化快速发展的时代,数据可视化和图表工具不仅对于程序员,也对于非技术背景的人士至关重要。绘图工具可以帮助我们更好地理解和表达复杂的概念或数据流。PlantUML和Mermaid是两款被广泛使用的绘图语言,它们都能够通过简洁的文本…...

leetcode 343. 整数拆分
题目 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。 示例 2: 输入: n 10 输出: 36 解释: 1…...
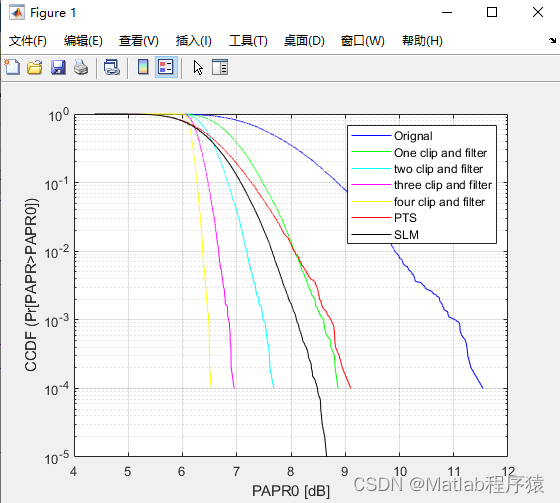
【MATLAB源码-第180期】基于matlab的PTS,SLM,CPFilter三种降低OFDM系统的PAPR仿真。
操作环境: MATLAB 2022a 1、算法描述 1. 限幅和滤波(Clipping and Filtering) 原理简介 限幅和滤波是一种基础且直观的方法,用于降低OFDM信号的PAPR。在限幅阶段,信号的幅度在达到设定阈值时会被削减,…...
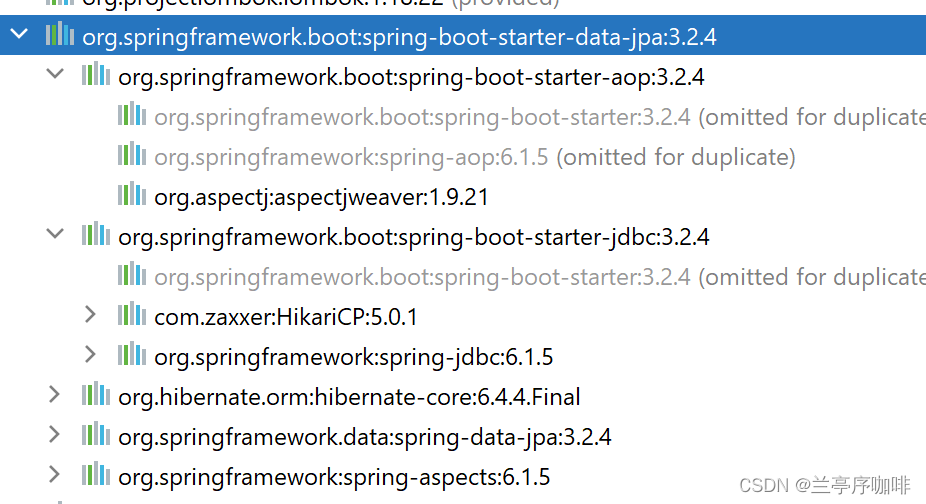
学透Spring Boot — 004. Spring Boot Starter机制和自动配置机制
如果你项目中一直用的是 Spring Boot,那么恭喜你没有经历过用 Spring 手动集成其它框架的痛苦。 都说 Spring Boot 大大简化了 Spring 框架开发 Web 应用的难度,这里我们通过配置 Hibernate 的两种方式来深刻体会这一点: 使用 Spring 框架集…...
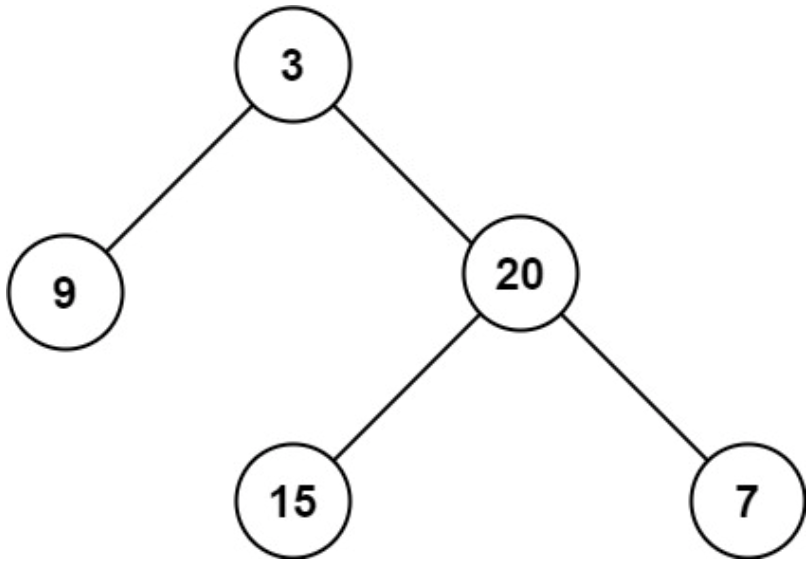
面试算法-170-二叉树的最大深度
题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 解 class Solution {public int maxDepth(TreeNod…...

【数据结构】哈希
文章目录 1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决4.1 闭散列4.2 开散列 unordered 系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。 1. 哈希概念 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系ÿ…...

Kubernetes(k8s)监控与报警(qq邮箱+钉钉):Prometheus + Grafana + Alertmanager(超详细)
Kubernetes(k8s)监控与报警(qq邮箱钉钉):Prometheus Grafana Alertmanager(超详细) 1、部署环境2、基本概念简介2.1、Prometheus简介2.2、Grafana简介2.3、Alertmanager简介2.4、Prometheus …...
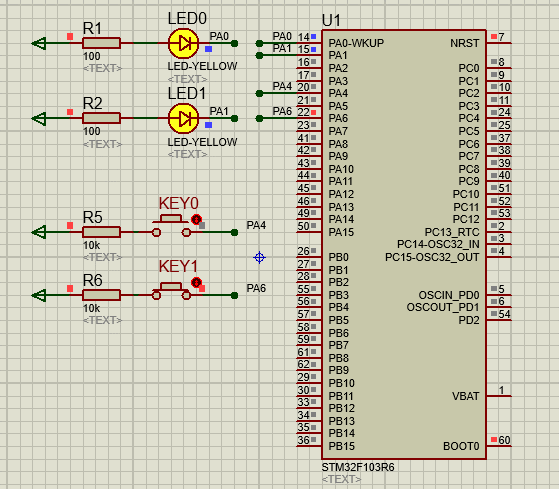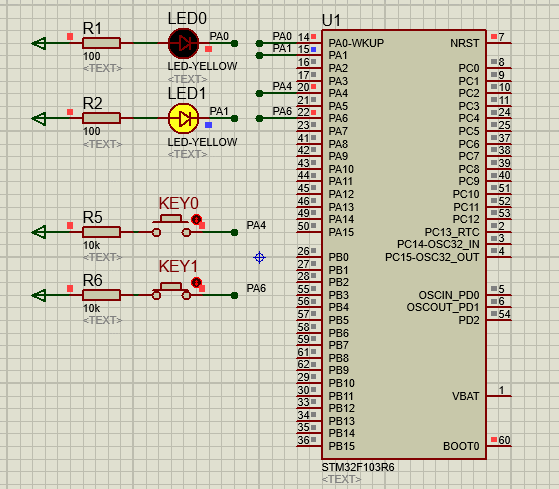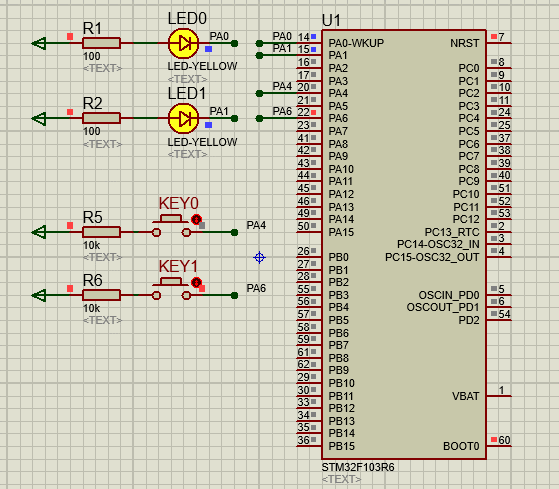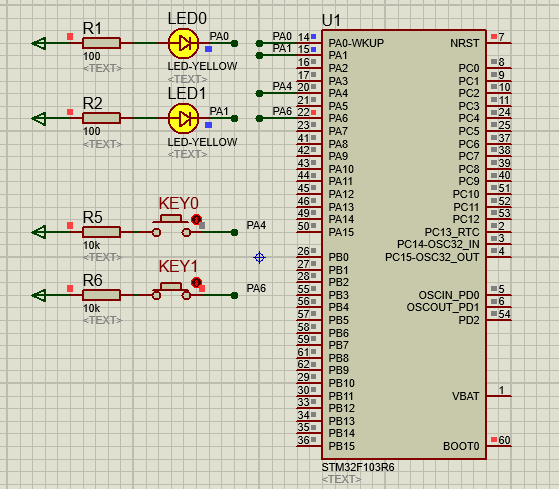
STM32-04基于HAL库(CubeMX+MDK+Proteus)中断案例(按键中断扫描)
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式,生成代码四、MDK打开生成项目,编写HAL库的按键检测代码五、运行仿真程序,调试代码 一、功能需求分析 在完成GPIO输入输出案例之后,开始新的功能…...
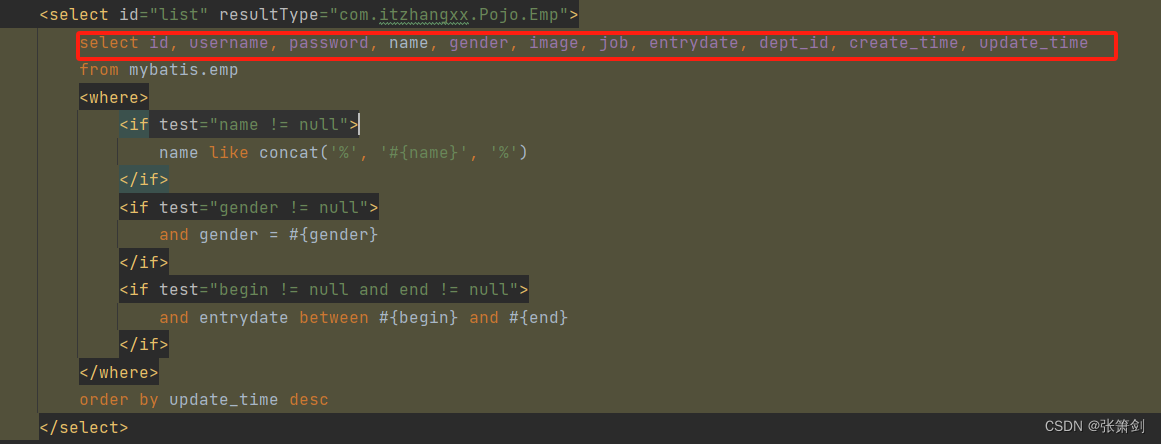
第十五篇:Mybatis
文章目录 一、什么是MyBatis二、Mybatis入门案例三、配置SQL提示四、数据库连接池四、lombok五、mybatis基础操作5.1 根据id删除5.2 预编译SQL5.3 新增员工5.4 更新员工5.5 查询员工(用于页面回显)5.6 条件查询 七、XML映射文件八、动态SQL8.1 if语句8.2…...
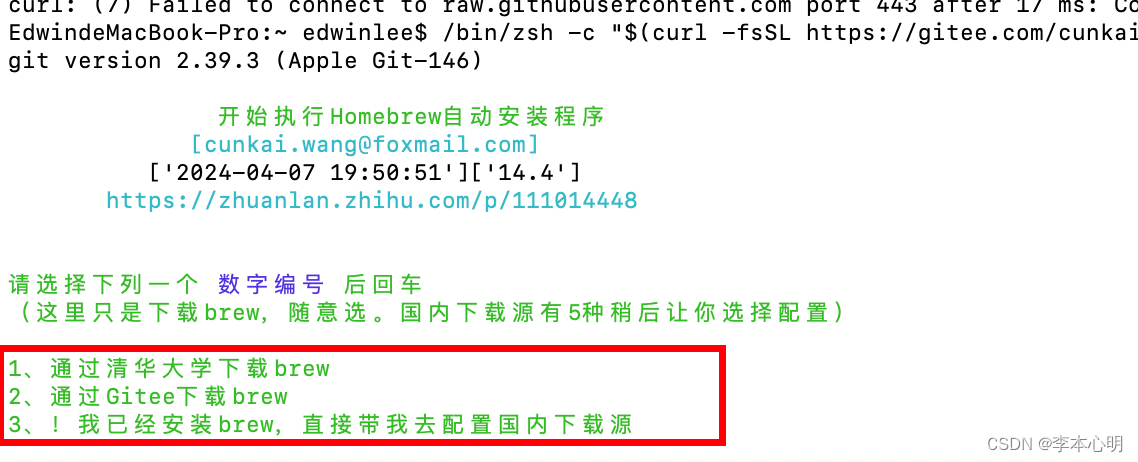
【MacBook系统homebrew镜像记录】
安装 使用Homebrew 国内源安装脚本,贼方便: /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"切换至清华大学镜像源: 命令合并: 分别切换了 brew.git、 homebrew-core.git、 homebrew-…...

深拷贝总结
JSON.parse(JSON.stringify(obj)) 这行代码的运行过程,就是利用 JSON.stringify 将js对象序列化(JSON字符串),再使用JSON.parse来反序列化(还原)js对象;序列化的作用是存储和传输。(…...

RabbitMQ在云原生环境中部署和应用实践
一、RabbitMQ和云原生技术的关系 RabbitMQ是一种开源的、实现了先进的消息队列协议(AMQP)的消息队列软件。而云原生技术就是为在公共云、私有云以及其他各种云环境提供应用的一种方法。RabbitMQ和云原生技术在分布式系统和微服务架构中都起到了关键作用…...
和上传至服务器)
flask 后端 + 微信小程序和网页两种前端:调用硬件(相机和录音)和上传至服务器
选择 flask 作为后端,因为后续还需要深度学习模型,python 语言最适配;而 flask 框架轻、学习成本低,所以选 flask 作为后端框架。 微信小程序封装了调用手机硬件的 api,通过它来调用手机的摄像头、录音机,…...
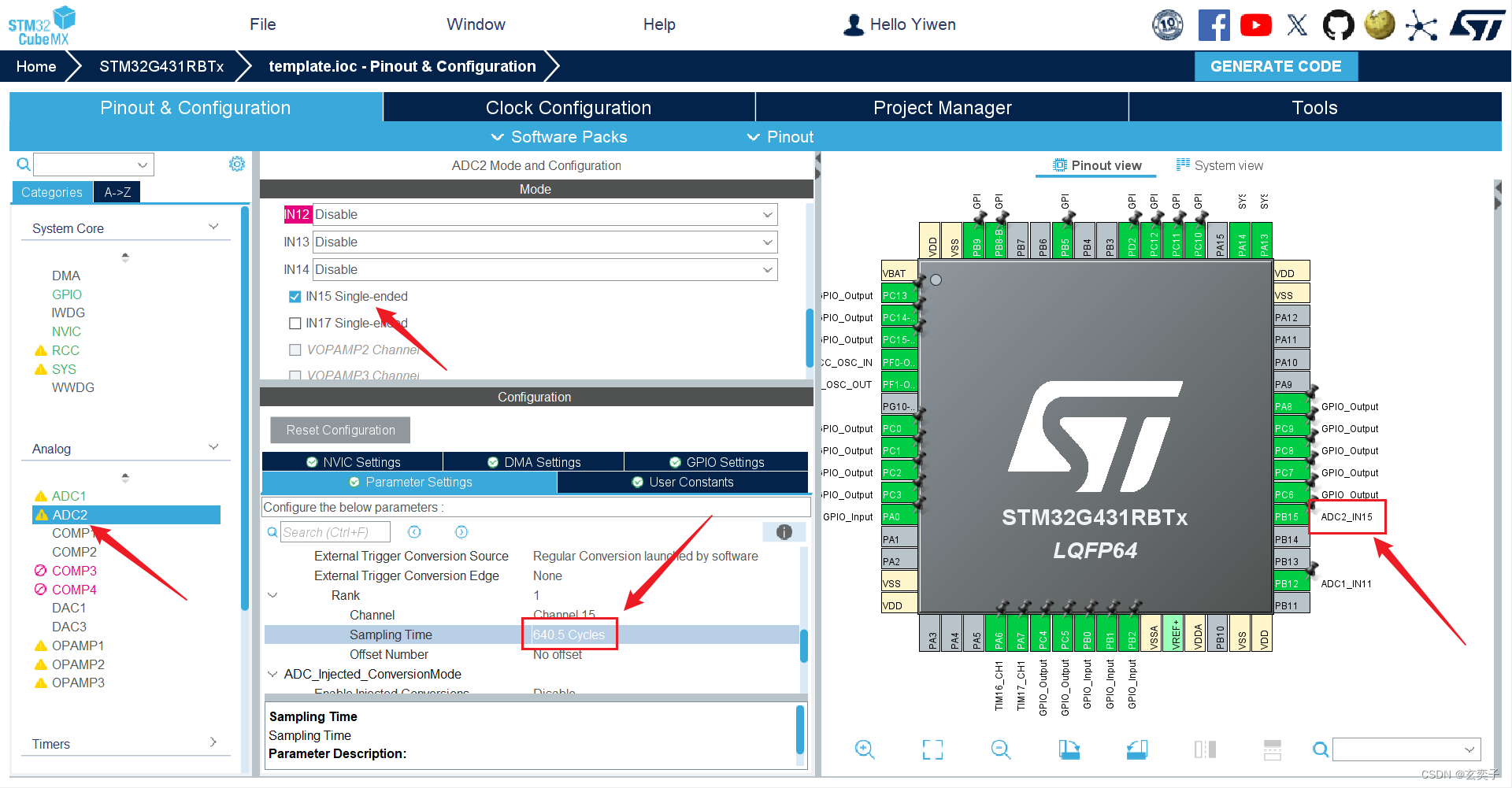
蓝桥杯嵌入式(G431)备赛笔记——ADC+LCD
目录 题目要求(真题): cubeMX配置: 小试牛刀: Keil代码: 效果演示: 题目要求(真题): 使用第十一届第二场真题,练习ADC波部分的代码 cubeMX配…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
