算法训练营第二十三天(二叉树完结)
算法训练营第二十三天(二叉树完结)
669. 修剪二叉搜索树
力扣题目链接(opens new window)
题目
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
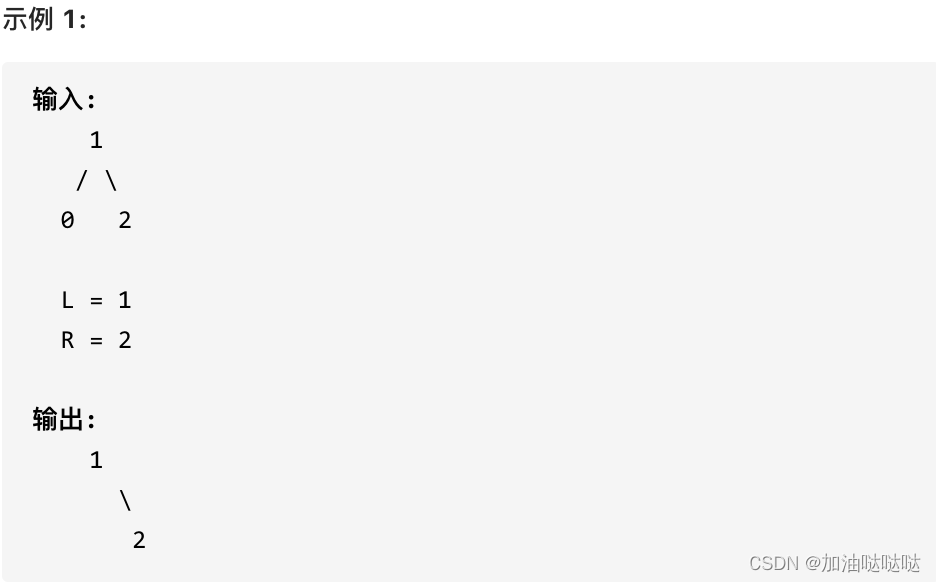

解答
自己写的递归
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null)return null;if (root.val == low){root.left = null;root.right = trimBST(root.right,low,high);}else if (root.val == high){root.right = null;root.left = trimBST(root.left,low,high);}else if (root.val > low && root.val < high){root.left = trimBST(root.left,low,high);root.right = trimBST(root.right,low,high);}else if (root.val < low)root = trimBST(root.right,low,high);elseroot = trimBST(root.left,low,high);return root;}
}
简化递归
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null)return null;if (root.val < low)root = trimBST(root.right,low,high);//左子树和根都不要了else if (root.val > high)root = trimBST(root.left,low,high);//右子树和根都不要了else {// root在[low,high]范围内root.left = trimBST(root.left,low,high);root.right = trimBST(root.right,low,high);}return root;}
}
迭代(看下图就理解了)
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if(root == null)return null;// 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭while(root != null && (root.val < low || root.val > high)){if(root.val < low)root = root.right;// 小于L往右走elseroot = root.left;// 大于R往左走}TreeNode curr = root;// 此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况while(curr != null){while(curr.left != null && curr.left.val < low){curr.left = curr.left.right;}curr = curr.left;}//go back to root;curr = root;// 此时root已经在[L, R] 范围内,处理右孩子大于R的情况while(curr != null){while(curr.right != null && curr.right.val > high){curr.right = curr.right.left;}curr = curr.right;}return root;}
}

108.将有序数组转换为二叉搜索树
力扣题目链接(opens new window)
题目
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:

解答
使用新的空间
class Solution {public TreeNode sortedArrayToBST(int[] nums) {if (nums.length == 0)return null;int midIndex = nums.length / 2;TreeNode root = new TreeNode(nums[midIndex]);root.left = sortedArrayToBST(Arrays.copyOfRange(nums,0,midIndex));root.right = sortedArrayToBST(Arrays.copyOfRange(nums,midIndex + 1,nums.length));return root;}
}
使用索引(左闭右开)
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return sortedArrayToBST(nums, 0, nums.length);}//左闭右开public TreeNode sortedArrayToBST(int[] nums, int left, int right) {if (left >= right) {return null;}if (right - left == 1) {return new TreeNode(nums[left]);}int mid = left + (right - left) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = sortedArrayToBST(nums, left, mid);root.right = sortedArrayToBST(nums, mid + 1, right);return root;}
}
538.把二叉搜索树转换为累加树
力扣题目链接(opens new window)
题目
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。
示例 1:
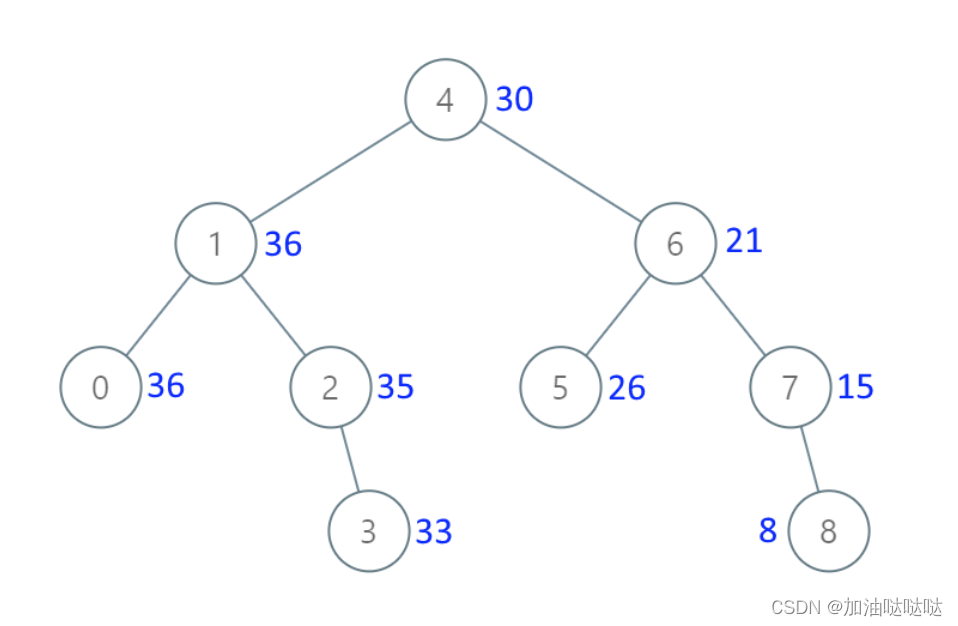
- 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
- 输入:root = [0,null,1]
- 输出:[1,null,1]
示例 3:
- 输入:root = [1,0,2]
- 输出:[3,3,2]
示例 4:
- 输入:root = [3,2,4,1]
- 输出:[7,9,4,10]
提示:
- 树中的节点数介于 0 和 104 之间。
- 每个节点的值介于 -104 和 104 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树
解答
- 采取中序遍历,不过是右中左,相当于从最大到最小遍历
- 对于每一个结点,他的值都等于他之前遍历的所有的值的和
- 下面的sum其实也相当于双指针中的pre,初始状态pre指向空,cur指向最右侧结点
递归
class Solution {int sum = 0;public TreeNode convertBST(TreeNode root) {travel(root);return root;}private void travel(TreeNode root){if (root == null)return;//右中左travel(root.right);root.val += sum;sum = root.val;travel(root.left);}
}
//不好理解
class Solution {public TreeNode convertBST(TreeNode root) {travel(root,0);return root;}private int travel(TreeNode root,int sum){if (root == null)return sum;//右中左root.val += travel(root.right,sum);return travel(root.left,root.val);//每次执行完都是为下一轮做准备}
}
迭代
class Solution {public TreeNode convertBST(TreeNode root) {//右中左Stack<TreeNode> stack = new Stack<>();int sum = 0;TreeNode cur = root;//右中左while (!stack.isEmpty() || cur != null){while (cur != null){stack.push(cur);cur = cur.right;}cur = stack.pop();cur.val += sum;sum = cur.val;cur = cur.left;}return root;}
}
相关文章:

算法训练营第二十三天(二叉树完结)
算法训练营第二十三天(二叉树完结) 669. 修剪二叉搜索树 力扣题目链接(opens new window) 题目 给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>L) 。你可能需要改…...
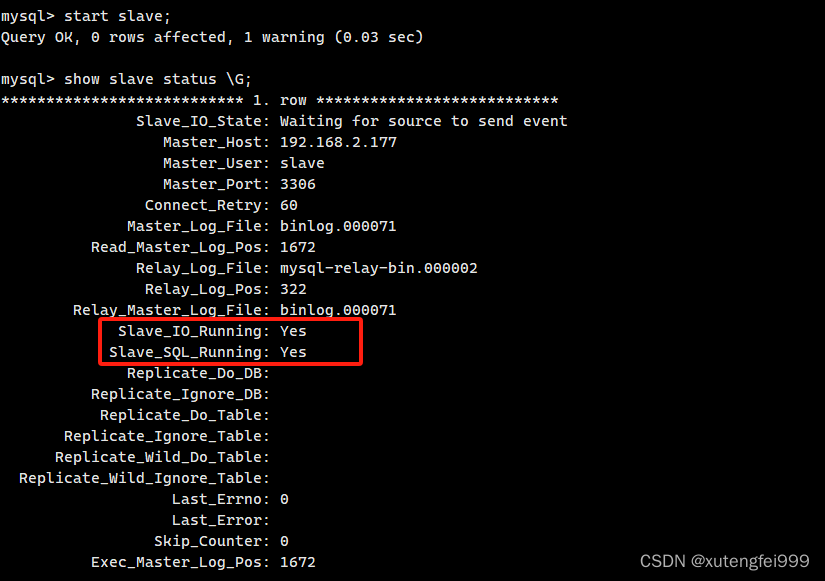
mysql主从复制Slave_SQL_Running: No
1、SHOW SLAVE STATUS \G; Slave_SQL_Running: No 解决方案: 重新同步主库和从库的数据 1、从库先停掉slave stop slave; 2、在主库查看此时的日志文件和位置 show master status; 3、在从库中执行 change master to master_host192.168.2.177,master_userslave…...
【SpringBoot】SpringBoot项目快速搭建
本文将介绍Springboot项目的快速搭建 快速创建SpringBoot项目 打开IDEA在File->New->Project中新建项目 点击左侧的Spring Initializr 输入以下信息: Name 项目名称Group 根据公司域名来,或者默认com.example【倒序域名】Package Name 包名&am…...
Terraform 状态不同步处理
背景 在使用 Terraform 创建 TencentCloud TKE 的时候,手贱把 node pool 删掉了。导致执行 destroy, plan 都会报错。 │ Error: [TencentCloudSDKError] CodeInternalError.UnexpectedInternal, Messagerelated node pool query err(get node pool failed: [E501…...
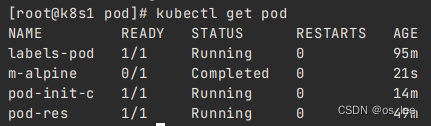
4.2.k8s的pod-标签管理、镜像拉取策略、容器重启策略、资源限制、优雅终止
一、标签管理 1.标签在k8s中极其重要,大多数资源的相互关联就需要使用标签;也就是说,资源的相互关联大多数时候,是使用标签进行关联的; 2.其他作用,在k8s集群中,node节点的一些操作比如污点及污…...

能源党建后台项目总结
1.引入 本次框架是Ruoyi-plusvue2element组合。 2.样式 由于是后台项目,样式要求统一,不可以有的输入框长有的短。着重几点: 1.关于form表单应该如何水平布局 在element中,form有个属性叫::inline"true"…...

股票高胜率的交易法则是什么?
股票交易中的高胜率交易法则并非一成不变,而是根据市场状况、个人投资风格和经验等多种因素综合而定的。以下是一些有助于提升交易胜率的法则和策略: 1.趋势跟踪法则:在股票交易中,趋势跟踪是一种有效的策略。通过观察大盘和个股…...
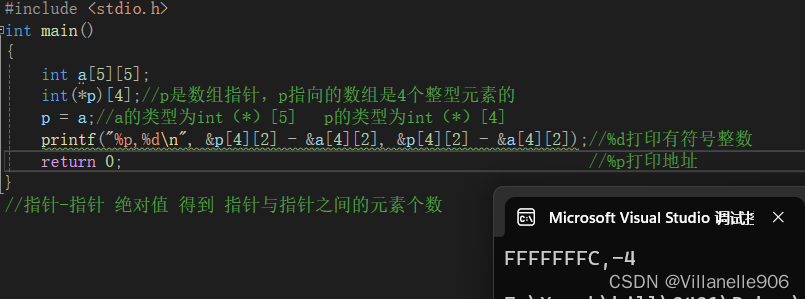
C语言 | sizeof与strlen的区别(附笔试题)
目录: 1. sizeof和strlen的对比 2. 数组和指针 笔试题解析 3. 指针运算 笔试题解析 内容多多,需耐心看完,加油!!! 一.sizeof和strlen的对比 1.1 sizeof 在学习操作符的时候,我们学习了 s…...

AI自动绘画器介绍和应用场景
AI自动绘画器是一种利用人工智能技术来生成绘画作品的工具。以下是一些常见的AI自动绘画器: DeepDream: 风格:可以生成三种风格的图片,包括深度梦幻风格、深度风格和浅层风格。应用场景:起初设计用于帮助研究人员理解…...

java二叉树前中后序遍历
代码随想录解题思路🆒力扣前序题目🆒力扣中序题目🆒力扣后序题目 递归遍历 // 前序遍历 class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res new ArrayList<>();preorder(root…...

【LeetCode刷题笔记】LeetCode 1365.有多少小于当前数字的数字
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 更多算法知识专栏:算法分析🔥 给大家跳段街舞感谢…...
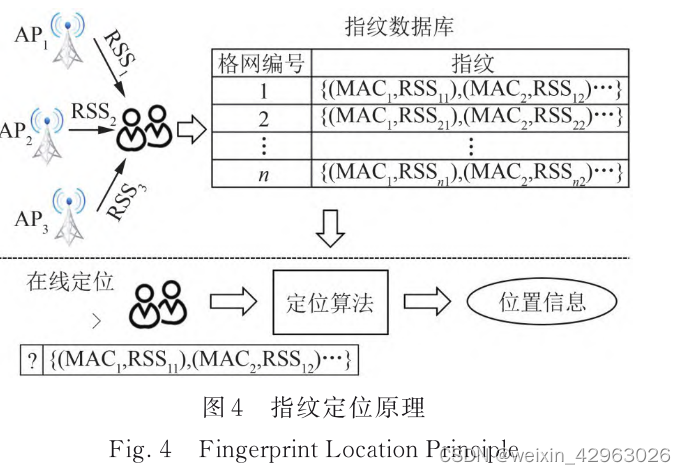
室内定位中文综述阅读
1 室内高精度定位技术总结与展望 [4]柳景斌,赵智博,胡宁松等.室内高精度定位技术总结与展望[J].武汉大学学报(信息科学 版),2022,47(07):997-1008.DOI:10.13203/j.whugis20220029. 1.1.1 WiFi‐RTT定位 2016 年 12 月,随着新版 IEEE802.11 标准的公布,…...

微信小程序uniapp+vue电力巡线任务故障报修管理系统2q91t
uni-app框架:使用Vue.js开发跨平台应用的前端框架,编写一套代码,可编译到Android、小程序等平台。 前端开发:vue 语言:javapythonnodejsphp均支持 运行软件:idea/eclipse/vscode/pycharm/wamp均支持 框架支持:Ssm/django/flask/t…...
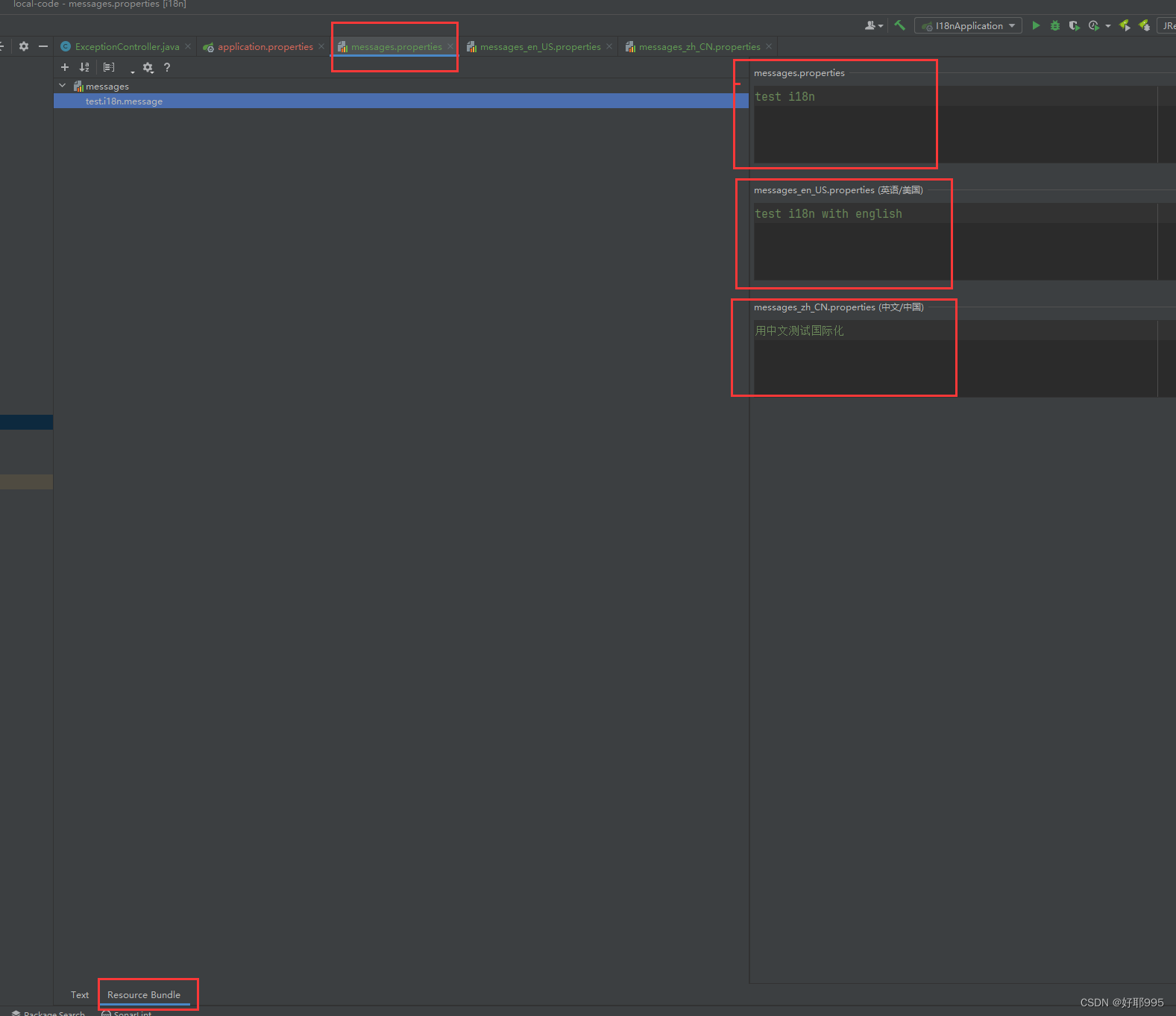
springboot国际化多语言
1,新建国际化多语言文件 在resources目录下新建 messages.properties 其他语言的文件 编辑messages.properties文件,下方从text切换到Resource Bundle ,即可对照着编辑多语言文件 (如果没有找到Resource Bundle,先在settings->plugins中安装Resource Bundle Editor) 2,配…...

set和map
这里是目录标题 setinsertfinderasecountlower_boundupper_boundmultisetset的应用 mappairinsertinsert的pair map的遍历map对[ ]的重载(重点)multimap set set的普通迭代器和const迭代器都不支持修改。(这点可以根据源代码看出来,都是对const iterator进行了type…...
Open CASCADE学习|求曲面的参数空间
在三维空间中,任意的曲面都可以通过特定的方法映射到一个二维参数平面上,从而对其进行详细的几何分析和处理。首先,我们需要从三维模型中提取出特定的曲面,这通常被称为“Face”。一个face可以被视为三维空间中的一个封闭区域&…...
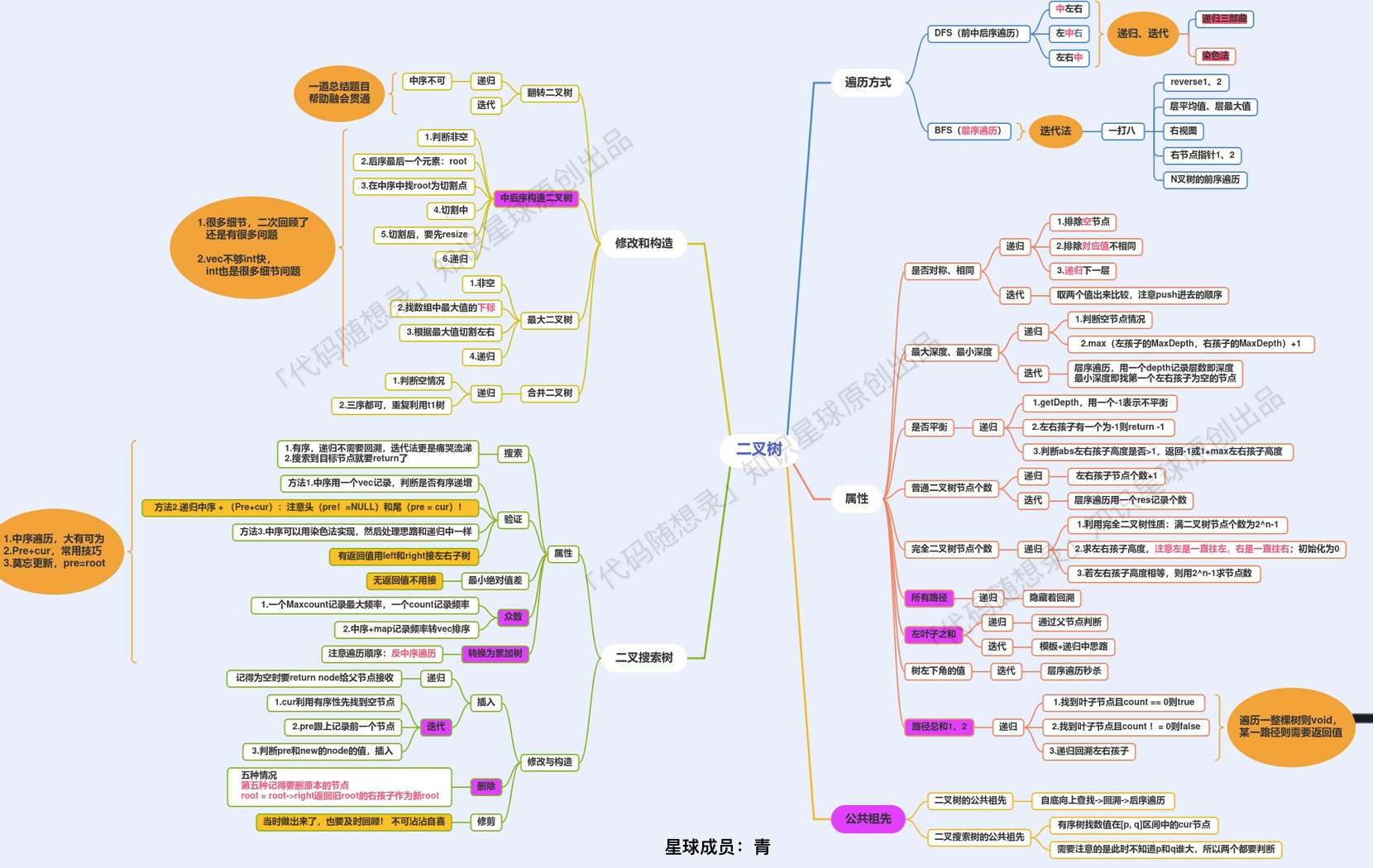
代码随想录阅读笔记-二叉树【总结】
二叉树的理论基础 代码随想录 (programmercarl.com):二叉树的种类、存储方式、遍历方式、定义方式 二叉树的遍历方式 深度优先遍历 代码随想录阅读笔记-二叉树【递归遍历】-CSDN博客:递归三部曲初次亮相代码随想录阅读笔记-二叉树【迭代遍历】-CSDN博…...

【SpringBoot整合系列】SpringBoot整合FastDFS(二)
目录 SpringBoot整合FastDFSJava客户端/依赖常用api接口解释1.uploadFile参数返回值 2.uploadSlaveFile参数返回值 3.getMetadata参数返回值 4.overwriteMetadata参数:返回值:无 5.mergeMetadata参数:返回值:无 6.queryFileInfo参…...

L2-2 巴音布鲁克永远的土(二分+并查集)
思路:我们可以二分答案,然后判断当前答案合不合理。 对于判断答案合理,可以用并查集,看mid能否把所有检查点连进一个集合中,枚举每个结点,如何当前结点周围的四个方向可以连的话,就加进同一个集…...

Spring Cloud学习笔记:Eureka简介,Eureka简单样例
这是本人学习的总结,主要学习资料如下 - 马士兵教育 [TOC](目录)1、Eureka 1.1、架构 Eureka是SpringCloud Nexflix的核心子模块,其中包含Server和Client。 Server提供服务注册,存储所有可用服务节点。 Client用于简化和Server的通讯复杂…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
