当前位置： 首页 > news >正文

如何从应用商店Microsoft Store免费下载安装HEVC视频扩展插件

news 2025/11/6 0:46:08

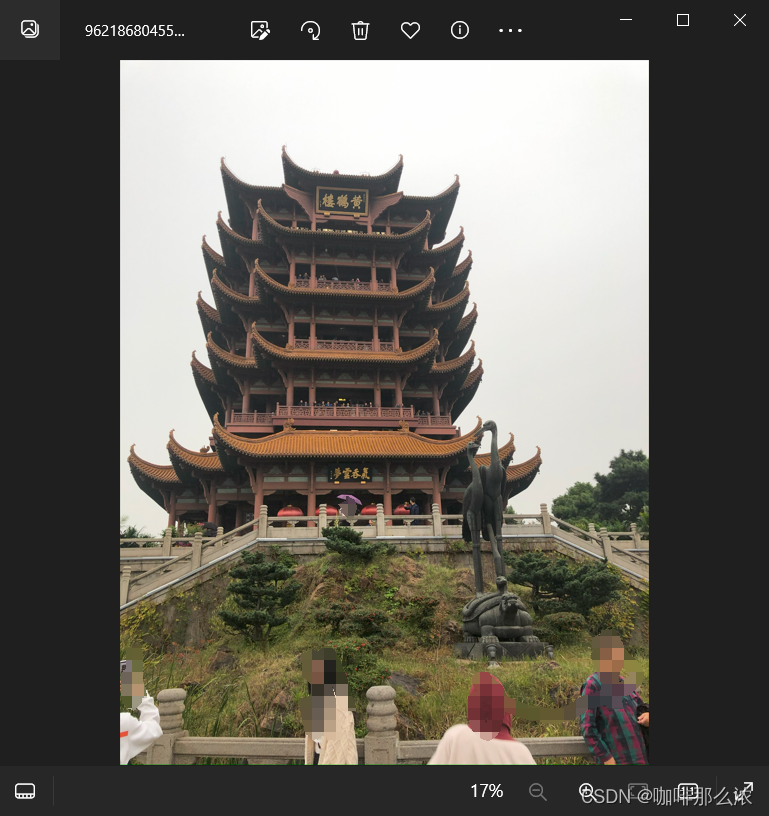
在电脑上打开一张HEIC类型的图片提示缺少HEVC解码器，无法打开查看，现象如下：
在这里插入图片描述
这种情况一般会提示我们需要下载安装HEVC解码器，点击“立即下载并安装”会跳转到应用商店，但是我们发现需要付费7元才能下载安装
在这里插入图片描述
免费安装的方法：

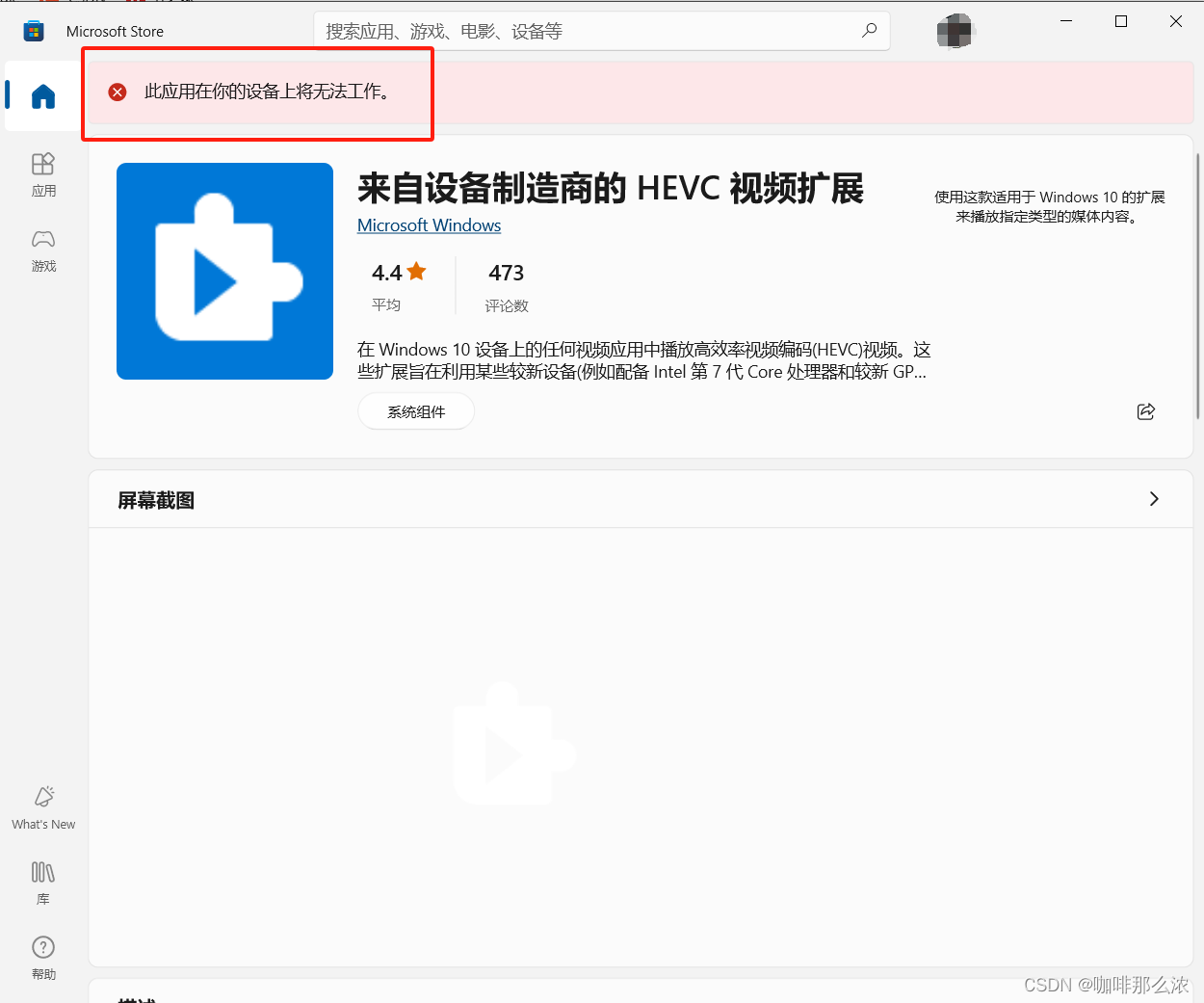
  • 1、浏览器打开以下链接，点击页面上的安装按钮，会跳转到应用商店，此时我们可以看到在商店的顶端提示“此应用在你的设备上将无法工作”，不用管这个提示。
    https://apps.microsoft.com/detail/9N4WGH0Z6VHQ?hl=zh-cn&gl=cn
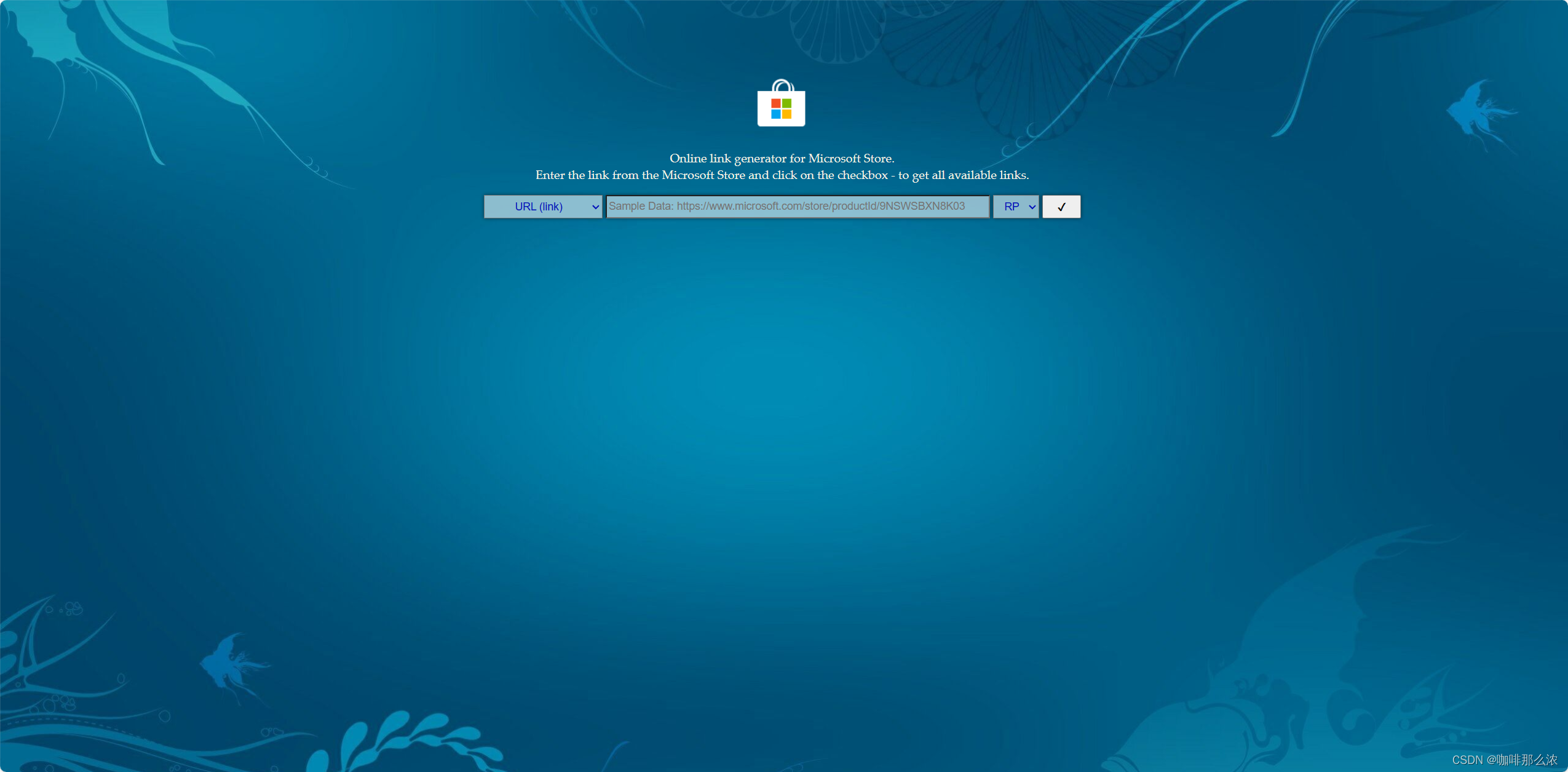
    在这里插入图片描述

  • 2、复制并在浏览器中打开以下链接
    https://store.rg-adguard.net/
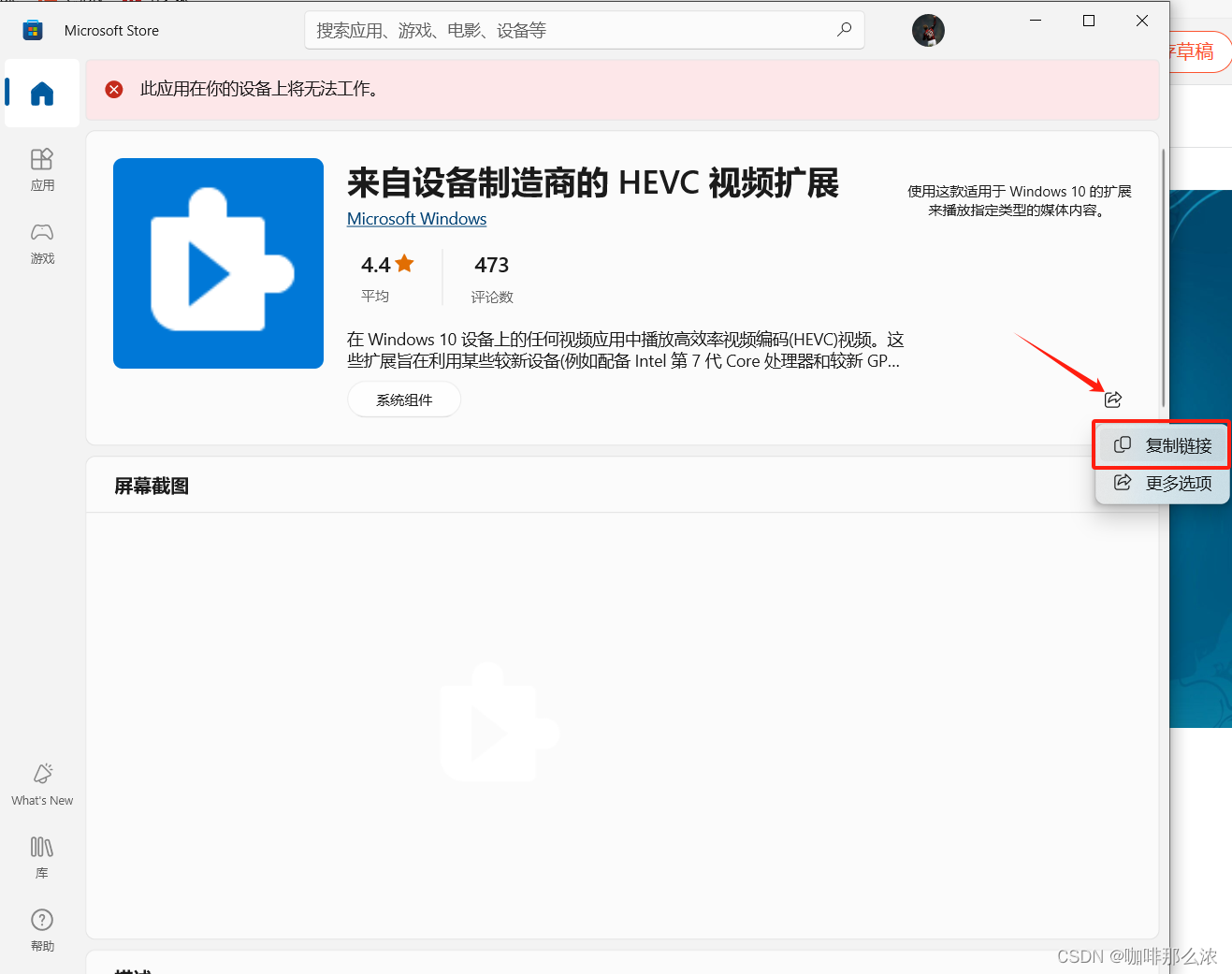
    在这里插入图片描述

  • 3、回到刚刚打开的应用商店，点击分享按钮，复制链接
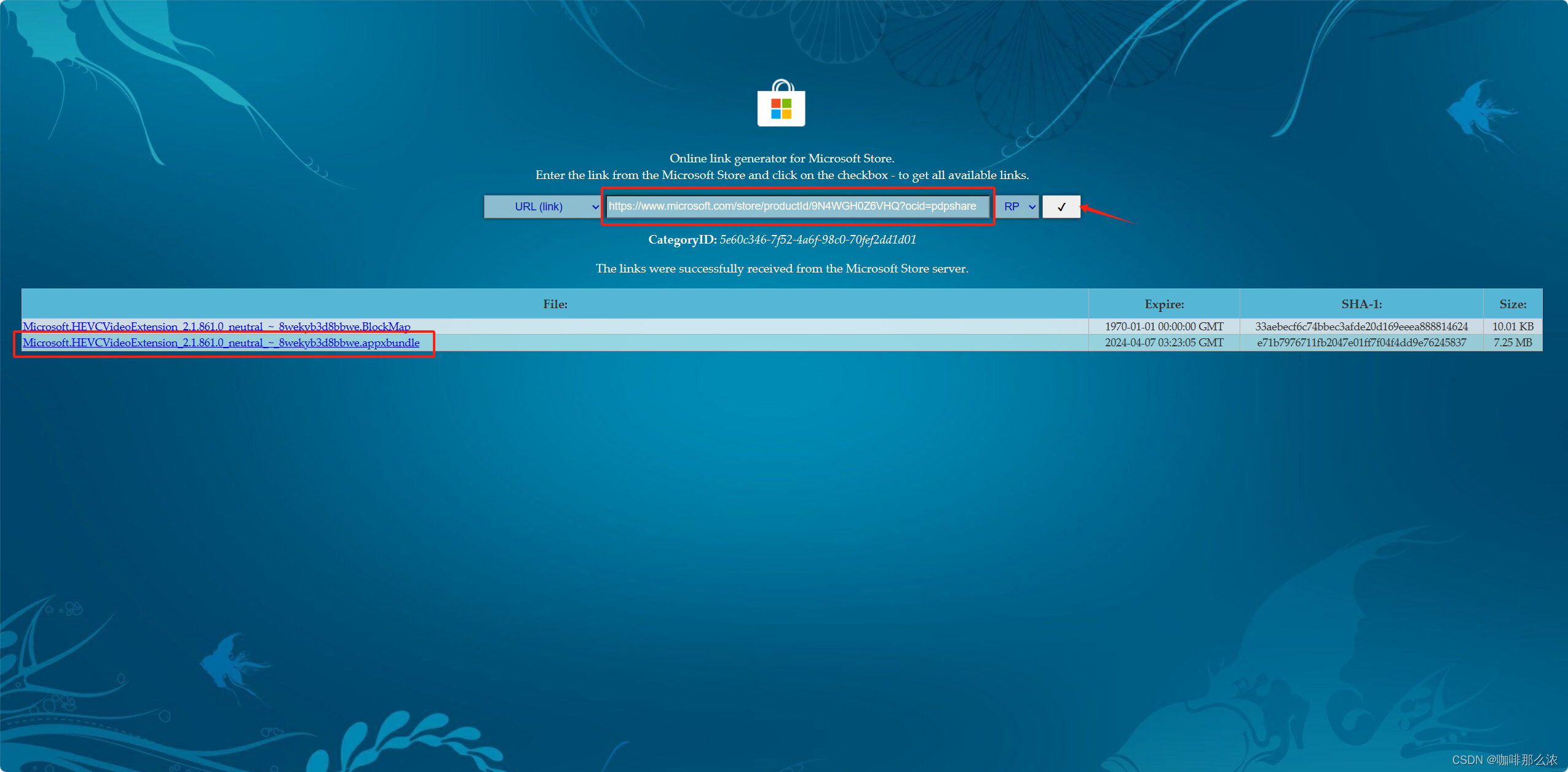
    在这里插入图片描述

  • 4、将复制到的链接填写到刚才打开的网站的输入框内，点击前往，点击结果中的第二个下载安装包
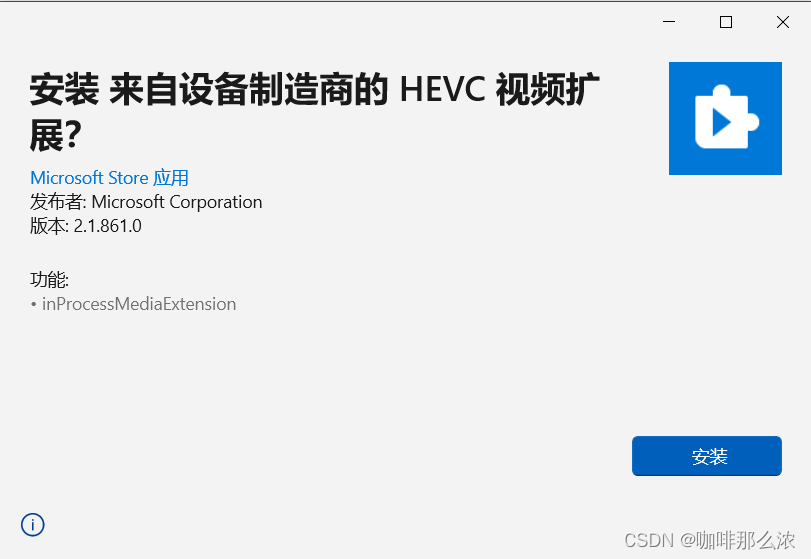
    在这里插入图片描述
    在这里插入图片描述

  • 5、安装刚才下载到的安装包
    在这里插入图片描述

  • 6、再次打开heic格式的图片，已经可以正常显示了
    在这里插入图片描述

相关文章：

如何从应用商店Microsoft Store免费下载安装HEVC视频扩展插件

在电脑上打开一张HEIC类型的图片提示缺少HEVC解码器，无法打开查看，现象如下： 这种情况一般会提示我们需要下载安装HEVC解码器，点击“立即下载并安装”会跳转到应用商店，但是我们发现需要付费7元才能下载安装 免费安装…...

编程日记 2024/4/12 14:55:59

【vue】v-if 条件渲染

v-if 不适用于频繁切换显示模式的场景 修改web.user&#xff0c;可看到条件渲染的效果 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initi…...

编程日记 2024/4/12 14:54:58

Day37:LeedCode 738.单调递增的数字 968.监控二叉树 蓝桥杯 翻转

738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时&#xff0c;我们称这个整数是单调递增的。 给定一个整数 n &#xff0c;返回 小于或等于 n 的最大数字&#xff0c;且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9 思路: 假设这个数是98,…...

编程日记 2024/4/12 14:49:51

详解Qt元对象系统

Qt库作为一款流行的跨平台C应用程序开发框架&#xff0c;其中的元对象系统是其核心特性之一。Qt元对象系统不仅提供了诸如信号槽&#xff08;Signals & Slots&#xff09;、属性系统&#xff08;Property System&#xff09;等功能&#xff0c;还实现了对C对象的运行时类型…...

编程日记 2024/4/12 14:48:50

无法用raven-js，如何直接使用TraceKit标准化错误字符串（一次有趣的探索）

引子&#xff1a;网上三年前&#xff08;2020&#xff09;的文章介绍了一个raven-js 简单说就是把堆栈信息格式化兼容各浏览器&#xff0c;便于查看错误来源。 **but&#xff1a;**到处找了一下raven-js&#xff0c;已经没有官方出处了&#xff0c;只在Sentry的源码仓库里发现…...

编程日记 2024/4/12 14:47:49

Docker学习笔记（二）：在Linux中部署Docker（Centos7下安装docker、环境配置，以及镜像简单使用）

一、前言 记录时间 [2024-4-6] 前置文章&#xff1a;Docker学习笔记&#xff08;一&#xff09;&#xff1a;入门篇&#xff0c;Docker概述、基本组成等&#xff0c;对Docker有一个初步的认识 在上文中&#xff0c;笔者进行了Docker概述&#xff0c;介绍其历史、优势、作用&am…...

编程日记 2024/4/12 14:45:33

uniapp 检查更新

概览 在uniapp中检查并更新应用&#xff0c;可以使用uni-app自带的更新机制。以下是一个简单的示例代码&#xff0c;用于在应用启动时检查更新&#xff1a; // 在App.vue或者其他合适的地方调用 onLaunch: function() {// 当uni-app初始化完成时执行// 判断平台const platfor…...

编程日记 2024/4/12 14:44:31

（Java）数据结构——正则表达式

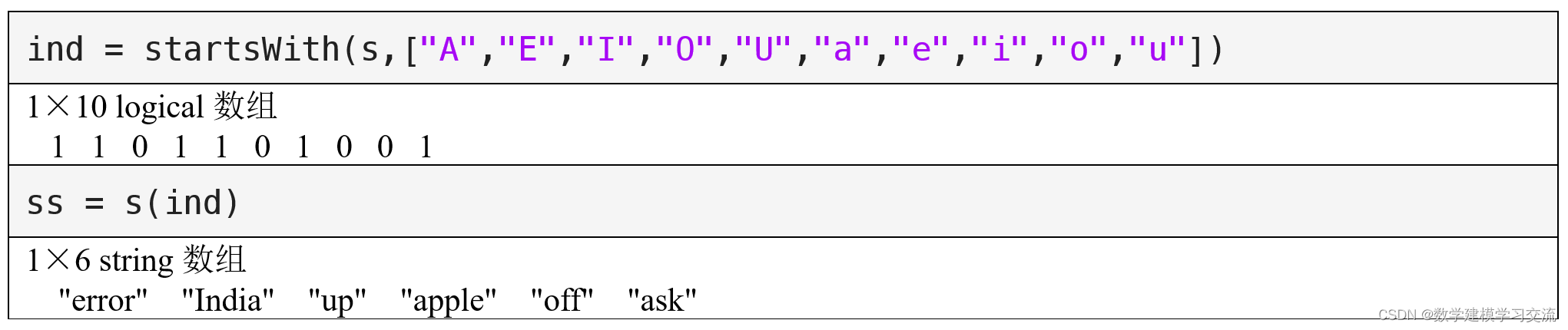
前言 本博客是博主用于复习数据结构以及算法的博客&#xff0c;如果疏忽出现错误&#xff0c;还望各位指正。 正则表达式概念 正则表达式&#xff0c;又称规则表达式&#xff08;Regular Expression&#xff09;&#xff0c;是一种文本模式&#xff0c;包括普通字符&#xf…...

编程日记 2024/4/12 14:42:28

第6章 6.3.1 正则表达式的语法（MATLAB入门课程）

讲解视频&#xff1a;可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。​ MATLAB教程新手入门篇&#xff08;数学建模清风主讲&#xff0c;适合零基础同学观看&#xff09;_哔哩哔哩_bilibili 正则表达式可以由一般的字符、转义字符、元字符、限定符等元素组…...

编程日记 2024/4/12 14:35:16

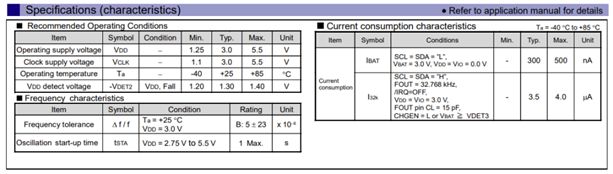
RX8130CE为用户提供带复位延迟和主备电管理的解决方案

实时时钟作为设备的精确时钟来源&#xff0c;其作用如同人的心脏&#xff0c;为设备提供准确稳定的心跳.而便携式设备由于应用场景多变&#xff0c;所以对内部元器件要求也相对较高&#xff0c;这就对作为核心器件的实时时钟模块提出不少挑战。EPSON实时钟模块产品线拥有丰富的…...

编程日记 2024/4/12 14:34:14

JS文件导出变量

如果 config.js 文件中有多个变量要导出&#xff0c;你可以按照以下步骤进行&#xff1a; 1. 在 config.js 文件中定义多个变量&#xff0c;并使用 export 导出它们。 // config.js const baseUrl "http://localhost:8081"; const apiKey "your_api_key&quo…...

编程日记 2024/4/12 14:33:11

已知私钥和密文,如何用python进行RSA解密

要使用Python进行RSA解密，你可以使用pycryptodome库。下面是一个简单的示例，展示了如何使用已知的私钥和密文进行RSA解密： 首先，确保你已经安装了pycryptodome库。如果没有安装，你可以通过运行pip install pycryptodome来安装它。 然后，你可以使用以下代码进行RSA解密：…...

编程日记 2024/4/12 14:29:07

vue2-vue3面试

v-text/v-html/v-once/v-show/v-if/v-for/v-bind/v-on beforeCreate() 已有DOM节点&#xff1a;可以data选项&#xff1a;不可以虚拟DOM节点&#xff1a;不可以 created():掌握 已有DOM节点&#xff1a;可以data选项&#xff1a;可以虚拟DOM节点&#xff1a;不可以 beforeMount…...

编程日记 2024/4/12 14:28:06

jmeter生成随机数的详细步骤及使用方式

Apache JMeter 是一个用于测试性能的开源工具&#xff0c;它可以模拟多种类型的负载并测量应用程序的性能。在 JMeter 中生成随机数可以通过使用预定义的函数来实现。以下是生成随机数的详细步骤及使用方式&#xff1a; 安装 JMeter&#xff1a; 首先&#xff0c;你需要在你的计…...

编程日记 2024/4/12 14:26:03

速盾：为什么会出现高防cdn?它适合哪些行业?

随着互联网的不断发展和普及&#xff0c;网络安全问题也变得日益突出。由于互联网的特性&#xff0c;许多企业和组织的在线业务往往面临来自网络攻击的威胁&#xff0c;如DDoS攻击、恶意爬虫等。为了保护在线业务的正常运行和用户数据的安全&#xff0c;高防CDN应运而生。 高防…...

编程日记 2024/4/12 14:22:58

GB∕T 25058-2019 信息安全技术 网络安全等级保护实施指南

GB∕T 25058-2019 信息安全技术 网络安全等级保护实施指南...

编程日记 2024/4/12 14:20:53

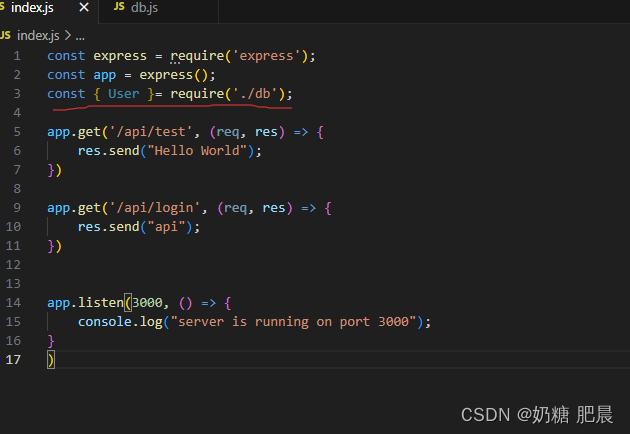
使用Nodejs + express连接数据库mongoose

文章目录 先创建一个js文档安装 MongoDB 驱动程序&#xff1a;引入 MongoDB 模块&#xff1a;设置数据库连接&#xff1a;新建一个表试试执行数据库操作&#xff1a;关闭数据库连接&#xff1a; 前面需要准备的内容可看前面的文章&#xff1a; Express框架搭建项目 node.js 简单…...

编程日记 2024/4/12 14:19:52

朗致集团面试-Java架构师

总结 三轮面试&#xff0c;第一轮是逻辑测试性格测试&#xff0c;第二轮是技术面试&#xff08;面试官-刘老师&#xff09;&#xff0c;第三轮是CTO面试&#xff08;面试官-屠老师&#xff09;。如果第三轮面试通过&#xff0c;考官会问你薪资意向&#xff0c;如果满意的话HR就…...

编程日记 2024/4/12 14:16:47

Ubuntu 23.10 搜狗拼音输入法闪屏解决

问题与解决 Ubuntu 23.10下安装搜狗拼音输入法并且使用搜狗输入法时&#xff0c;会闪屏。站内有人说可以换使用Xorg作为桌面服务&#xff0c;然后使用基于X11的桌面&#xff0c;其实可以不用那么麻烦&#xff0c;只需要设置QT的环境变量QT_QPA_PLATFORMxcb&#xff0c;然后重新…...

编程日记 2024/4/12 14:12:41

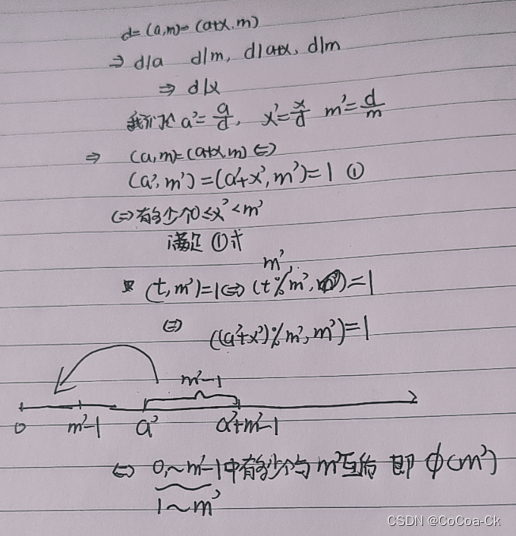
备战蓝桥杯---刷杂题2

显然我们直接看前一半&#xff0c;然后我们按照斜行看&#xff0c;我们发现斜行是递增的&#xff0c;而同一行从左向右也是递增的&#xff0c;因此我们可以直接二分&#xff0c;同时我们发现对称轴的数为Ck,2k. 我们从16斜行枚举即可 #include<bits/stdc.h> using name…...

编程日记 2024/4/12 14:10:39

华为云AI开发平台ModelArts

华为云ModelArts&#xff1a;重塑AI开发流程的“智能引擎”与“创新加速器”&#xff01; 在人工智能浪潮席卷全球的2025年&#xff0c;企业拥抱AI的意愿空前高涨&#xff0c;但技术门槛高、流程复杂、资源投入巨大的现实&#xff0c;却让许多创新构想止步于实验室。数据科学家…...

编程新知 2025/11/5 22:32:32

网络六边形受到攻击

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 抽象 现代智能交通系统 &#xff08;ITS&#xff09; 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 &#xff08;…...

编程新知 2025/11/4 3:06:30

C++实现分布式网络通信框架RPC(3)--rpc调用端

目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中&#xff0c;我们已经大致实现了rpc服务端的各项功能代…...

编程新知 2025/10/29 11:04:36

Linux链表操作全解析

Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表&#xff1f;1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

编程新知 2025/8/28 9:42:18

VB.net复制Ntag213卡写入UID

本示例使用的发卡器&#xff1a;https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

编程新知 2025/10/24 16:29:44

day52 ResNet18 CBAM

在深度学习的旅程中&#xff0c;我们不断探索如何提升模型的性能。今天&#xff0c;我将分享我在 ResNet18 模型中插入 CBAM&#xff08;Convolutional Block Attention Module&#xff09;模块&#xff0c;并采用分阶段微调策略的实践过程。通过这个过程&#xff0c;我不仅提升…...

编程新知 2025/9/14 16:40:54

第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明

AI 领域的快速发展正在催生一个新时代&#xff0c;智能代理&#xff08;agents&#xff09;不再是孤立的个体&#xff0c;而是能够像一个数字团队一样协作。然而&#xff0c;当前 AI 生态系统的碎片化阻碍了这一愿景的实现&#xff0c;导致了“AI 巴别塔问题”——不同代理之间…...

编程新知 2025/10/28 15:49:23

tree 树组件大数据卡顿问题优化

问题背景 项目中有用到树组件用来做文件目录&#xff0c;但是由于这个树组件的节点越来越多&#xff0c;导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多&#xff0c;导致的浏览器卡顿&#xff0c;这里很明显就需要用到虚拟列表的技术&…...

编程新知 2025/11/1 4:12:04

手机平板能效生态设计指令EU 2023/1670标准解读

手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读&#xff0c;综合法规核心要求、最新修正及企业合规要点&#xff1a; 一、法规背景与目标 生效与强制时间 发布于2023年8月31日&#xff08;OJ公报&…...

编程新知 2025/10/25 23:25:23

【WebSocket】SpringBoot项目中使用WebSocket

1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖&#xff0c;添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

编程新知 2025/9/20 3:28:39