R语言计算:t分布及t检验
t分布理论基础
t分布也称Student’s t-distribution,主要出现在小样本统计推断中,特别是当样本量较小且总体标准差未知时,用于估计正态分布的均值。其定义基于正态分布和 X 2 X^{2} X2分布(卡方分布)。如果随机变量X服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),而 Y Y Y服从自由度为 n n n的卡方分布,且 X X X与 Y Y Y相互独立,那么变量 T = Y n T = \sqrt{\frac{Y}{n}} T=nY 服从自由度( v v v)为 n n n的 t t t分布,其形状会随着自由度的变化而变化,t分布的形状会随自由度的变化而变化,当自由度较小时,t分布曲线较为平坦,且尾部较高,随着自由度的增加,t分布曲线逐渐接近正态分布曲线。
通常在大样本且假设总体标准差是已知的情况下使用正态分布,在小样本且总体标准差未知的情况下使用 t t t分布,特别是在进行假设检验和估计总体均值时。
t t t分布计算公式
T = X ˉ − μ S n . T = \sqrt{\frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}}}. T=nSXˉ−μ.
其中:
X ˉ \bar{X} Xˉ:样本均值;
μ \mu μ:假设的总体均值;
S S S:样本标准差;
n n n:样本大小.
t检验理论基础
t t t检验利用 t t t分布的性质来判断样本均值之间的差异是否显著, t t t检验是一种统计假设检验方法,它利用t分布理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。t检验通常用于检验样本均值与某个已知值或两个样本均值间是否存在显著差异的统计方法,在进行 t t t检验时,会计算出一个 t t t统计量,该统计量服从 t t t分布。
单样本t检验
用于检验单个样本的均值是否与已知的某个值存在显著差异
t = x ˉ − μ 0 s / n . t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}}. t=s/nxˉ−μ0.
其中:
x ˉ \bar{x} xˉ是样本均值,
μ 0 \mu_0 μ0是假设的总体均值,
s s s是样本标准差,
n n n是样本量。
双样本t检验
用于检验两个独立样本的均值是否存在显著差异。
t = x ˉ 1 − x ˉ 2 s 1 2 n 1 + s 2 2 n 2 . t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}. t=n1s12+n2s22xˉ1−xˉ2.
其中:
x ˉ 1 \bar{x}_{1} xˉ1、 x ˉ 2 \bar{x}_{2} xˉ2:两个样本的均值;
s 1 、 s_{1}、 s1、s_{2}$:两个样本的标准差;
n 1 n_{1} n1、 n 2 n_{2} n2分别是两个样本的样本量。
配对样本t检验
用于检验两个相关样本(同一组对象在不同条件下的测量值)。
t = d ˉ − μ d s d / n . t = \frac{\bar{d} - \mu_d}{s_d/\sqrt{n}}. t=sd/ndˉ−μd.
其中:
d ˉ \bar{d} dˉ:差值的均值;
μ d \mu_d μd:假设的差值均值(通常为0);
s d s_d sd:差值的标准差;
n n n:配对数据的数量。
R语言实现
使用R语言绘制 t t t分布曲线图
# 设置自由度
df <- 5 curve(dt(x, df), from = -5, to = 5, xlab = "t值", ylab = "概率密度", main = paste("t分布曲线图 (df =", df, ")"), col = "blue", lwd = 2)
grid(col="gray", lty="dotted")
abline(v=0, col="gray")
abline(h=0, col="gray")
polygon(c(-5, seq(-5, 5, length=200), 5), c(0, dt(seq(-5, 5, length=200), df), 0), col="lightblue", border=NA)
生成图形

t t t分布单尾曲线图
df <- 5 # t > 0
curve(dt(x, df), from = 0, to = 5, xlab = "t值", ylab = "概率密度", main = paste("t分布单尾曲线图 (df =", df, ")"), col = "blue", lwd = 2, xlim = c(0, 5))
grid(col = "gray", lty = "dotted")
polygon(c(0, seq(0, 5, length = 200), 5), c(0, dt(seq(0, 5, length = 200), df), 0), col = "lightblue", border = NA)

t t t分布双尾曲线图
df <- 5 curve(dt(x, df), from = -5, to = 5, xlab = "t值", ylab = "概率密度", main = paste("t分布双尾曲线图 (df =", df, ")"), col = "blue", lwd = 2)
grid(col = "gray", lty = "dotted")
# t < -2
polygon(c(-5, seq(-5, -2, length = 200), -2), c(0, dt(seq(-5, -2, length = 200), df), 0), col = "blue", border = NA)
polygon(c(2, seq(2, 5, length = 200), 5), c(0, dt(seq(2, 5, length = 200), df), 0), col = "blue", border = NA)
 单样品t检验
单样品t检验
单样品t检验用于检验单个样本的均值与已知的某个值(通常是理论值或标准值)是否有显著差异。
# 检验数据的均值是否与某个已知值(比如10)有显著差异
data <- c(9.8, 10.2, 9.9, 10.1, 10.0, 9.7, 10.3)print(t.test(data, mu = 10))
输出
One Sample t-testdata: data
t = 0, df = 6, p-value = 1
alternative hypothesis: true mean is not equal to 10
95 percent confidence interval:9.80021 10.19979
sample estimates:
mean of x 10
根据输出的报告可以看出:
t值=0,样本均值与假设的均值(在这里是10)之间没有差异。
自由度=6,对于单样本t检验, d f = n − 1 df = n - 1 df=n−1, n n n是样本数量。
p值=1,不能拒绝样本均值与10没有显著差异的原假设。
置信区间=95%。
双样品t检验
用于比较两个独立样本的均值是否存在显著差异。
# 现有两组独立的数据,比较这两组数据的均值是否有显著差异
data1 <- c(9.8, 10.2, 9.9, 10.1, 10.0)
data2 <- c(9.5, 9.6, 9.7, 9.9, 9.8, 10.0, 9.7, 9.8)print(t.test(data1, data2))
输出
Welch Two Sample t-testdata: data1 and data2
t = 2.7584, df = 8.7335, p-value = 0.02279
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:0.04401691 0.45598309
sample estimates:
mean of x mean of y 10.00 9.75
根据输出的报告可以看出:
t值=2.7584,在双样本t检验中,t值用于衡量两组数据的均值之间的差异,相对于它们的合并标准误差来说是否显著。
自由度=8.7335,对于双样本t检验,使用Welch公式对两个样本的大小和方差进行调整计算得出。
p值=0.02279,这小于常用的显著性水平0.05,两组数据的均值存在显著差异。
置信区间=95%。
根据R语言的输出报告显示,可以拒绝两组数据均值相同的原假设。
配对样品t检验
配对样品t检验用于比较同一组观测对象在不同条件下的测量值是否存在显著差异。
# 现有一组观测对象在两种不同条件下的测量值,检验这两种条件下测量值的均值是否有显著差异
data1 <- c(5.1, 5.5, 5.3, 5.6, 5.4)
data2 <- c(4.8, 5.0, 5.2, 5.4, 5.1)print(t.test(data2, data1, paired = TRUE))
输出
Paired t-testdata: data2 and data1
t = -4.2212, df = 4, p-value = 0.01347
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:-0.46416853 -0.09583147
sample estimates:
mean difference -0.28
t值=-4.2212,在配对t检验中,t值用于衡量配对观测值之间的差异是否显著,第一组数据的均值小于第二组。
自由度=4。
p值=0.01347,由于p值小于常用的显著性水平0.05,我们可以拒绝两组数据的均值差异为0的原假设,认为两组数据的均值存在显著差异。
置信区间=95%,对于两组数据的均值差异,有95%的信心认为这个差异在-0.46416853到-0.09583147之间。
样本估计=-0.28。配对数据中计算出的实际均值差异。
相关文章:

R语言计算:t分布及t检验
t分布理论基础 t分布也称Student’s t-distribution,主要出现在小样本统计推断中,特别是当样本量较小且总体标准差未知时,用于估计正态分布的均值。其定义基于正态分布和 X 2 X^{2} X2分布(卡方分布)。如果随机变量X服…...

uni-app的地图定位与距离测算功能的实现
文章目录 一、引言二、uni-app地图定位实现三、距离测算技术四、完整代码五、结论本文着重探讨了如何在uni-app中实现地图定位,以及如何计算当前定位与目标位置之间的距离。 一、引言 在移动应用开发中,地图定位与距离测算是常见的功能需求。无论是出行导航、位置签到,还是…...
如何从应用商店Microsoft Store免费下载安装HEVC视频扩展插件
在电脑上打开一张HEIC类型的图片提示缺少HEVC解码器,无法打开查看,现象如下: 这种情况一般会提示我们需要下载安装HEVC解码器,点击“立即下载并安装”会跳转到应用商店,但是我们发现需要付费7元才能下载安装 免费安装…...

【vue】v-if 条件渲染
v-if 不适用于频繁切换显示模式的场景 修改web.user,可看到条件渲染的效果 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initi…...

Day37:LeedCode 738.单调递增的数字 968.监控二叉树 蓝桥杯 翻转
738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9 思路: 假设这个数是98,…...

详解Qt元对象系统
Qt库作为一款流行的跨平台C应用程序开发框架,其中的元对象系统是其核心特性之一。Qt元对象系统不仅提供了诸如信号槽(Signals & Slots)、属性系统(Property System)等功能,还实现了对C对象的运行时类型…...

无法用raven-js,如何直接使用TraceKit标准化错误字符串(一次有趣的探索)
引子:网上三年前(2020)的文章介绍了一个raven-js 简单说就是把堆栈信息格式化兼容各浏览器,便于查看错误来源。 **but:**到处找了一下raven-js,已经没有官方出处了,只在Sentry的源码仓库里发现…...

Docker学习笔记(二):在Linux中部署Docker(Centos7下安装docker、环境配置,以及镜像简单使用)
一、前言 记录时间 [2024-4-6] 前置文章:Docker学习笔记(一):入门篇,Docker概述、基本组成等,对Docker有一个初步的认识 在上文中,笔者进行了Docker概述,介绍其历史、优势、作用&am…...

uniapp 检查更新
概览 在uniapp中检查并更新应用,可以使用uni-app自带的更新机制。以下是一个简单的示例代码,用于在应用启动时检查更新: // 在App.vue或者其他合适的地方调用 onLaunch: function() {// 当uni-app初始化完成时执行// 判断平台const platfor…...
数据结构——正则表达式)
(Java)数据结构——正则表达式
前言 本博客是博主用于复习数据结构以及算法的博客,如果疏忽出现错误,还望各位指正。 正则表达式概念 正则表达式,又称规则表达式(Regular Expression),是一种文本模式,包括普通字符…...
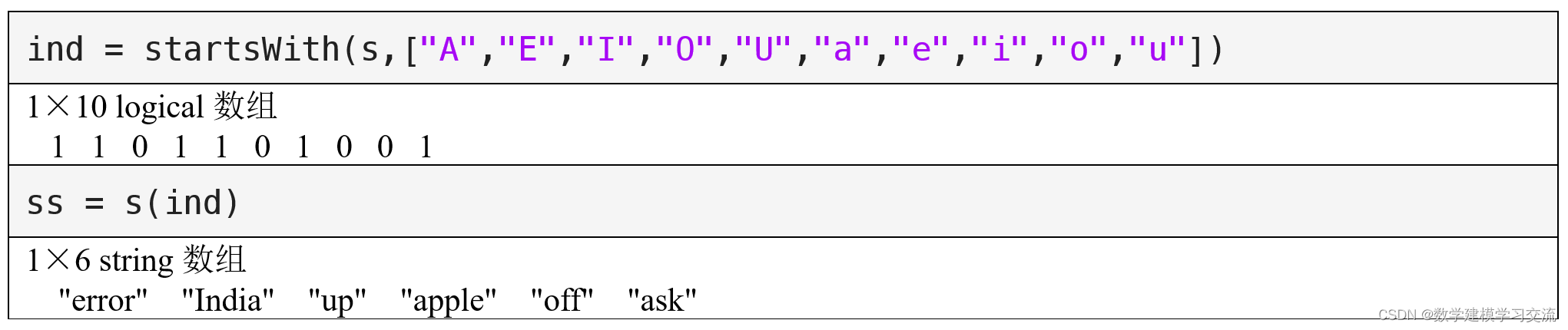
第6章 6.3.1 正则表达式的语法(MATLAB入门课程)
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 正则表达式可以由一般的字符、转义字符、元字符、限定符等元素组…...
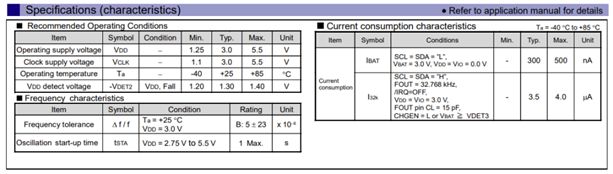
RX8130CE为用户提供带复位延迟和主备电管理的解决方案
实时时钟作为设备的精确时钟来源,其作用如同人的心脏,为设备提供准确稳定的心跳.而便携式设备由于应用场景多变,所以对内部元器件要求也相对较高,这就对作为核心器件的实时时钟模块提出不少挑战。EPSON实时钟模块产品线拥有丰富的…...

JS文件导出变量
如果 config.js 文件中有多个变量要导出,你可以按照以下步骤进行: 1. 在 config.js 文件中定义多个变量,并使用 export 导出它们。 // config.js const baseUrl "http://localhost:8081"; const apiKey "your_api_key&quo…...

已知私钥和密文,如何用python进行RSA解密
要使用Python进行RSA解密,你可以使用pycryptodome库。下面是一个简单的示例,展示了如何使用已知的私钥和密文进行RSA解密: 首先,确保你已经安装了pycryptodome库。如果没有安装,你可以通过运行pip install pycryptodome来安装它。 然后,你可以使用以下代码进行RSA解密:…...

vue2-vue3面试
v-text/v-html/v-once/v-show/v-if/v-for/v-bind/v-on beforeCreate() 已有DOM节点:可以data选项:不可以虚拟DOM节点:不可以 created():掌握 已有DOM节点:可以data选项:可以虚拟DOM节点:不可以 beforeMount…...

jmeter生成随机数的详细步骤及使用方式
Apache JMeter 是一个用于测试性能的开源工具,它可以模拟多种类型的负载并测量应用程序的性能。在 JMeter 中生成随机数可以通过使用预定义的函数来实现。以下是生成随机数的详细步骤及使用方式: 安装 JMeter: 首先,你需要在你的计…...

速盾:为什么会出现高防cdn?它适合哪些行业?
随着互联网的不断发展和普及,网络安全问题也变得日益突出。由于互联网的特性,许多企业和组织的在线业务往往面临来自网络攻击的威胁,如DDoS攻击、恶意爬虫等。为了保护在线业务的正常运行和用户数据的安全,高防CDN应运而生。 高防…...

GB∕T 25058-2019 信息安全技术 网络安全等级保护实施指南
GB∕T 25058-2019 信息安全技术 网络安全等级保护实施指南...
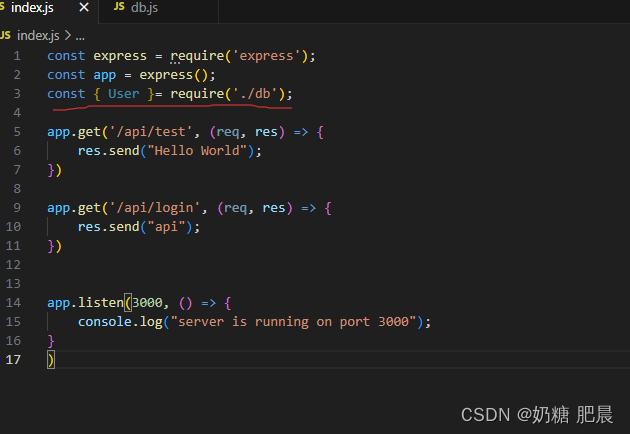
使用Nodejs + express连接数据库mongoose
文章目录 先创建一个js文档安装 MongoDB 驱动程序:引入 MongoDB 模块:设置数据库连接:新建一个表试试执行数据库操作:关闭数据库连接: 前面需要准备的内容可看前面的文章: Express框架搭建项目 node.js 简单…...

朗致集团面试-Java架构师
总结 三轮面试,第一轮是逻辑测试性格测试,第二轮是技术面试(面试官-刘老师),第三轮是CTO面试(面试官-屠老师)。如果第三轮面试通过,考官会问你薪资意向,如果满意的话HR就…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
