tcp early retransmit 和 rack 中神奇的 1/4 minrtt
雨中跑步十公里，沿河看柳，发了一则朋友圈：
为什么采用 1/4 minrtt 作为重传和探测的延时，上图解释的已经很清楚了，主要还是怕乱序，关于乱序的度量，上图解释得非常清楚，乱序预期可在 0.5rtt/w(相邻两个报文乱序) 到 0.5rtt(满载管道首尾报文乱序) 之间被检测到。
不管是 early retrans 前，还是 rack 判定一个报文丢失前，都要等待至少 1/4 个 minrtt，以确认事实或在此期待时间内反悔。如果 1/4 minrtt 还不足以断定，即采取措施，对于 rack 而言将延展乱序窗口，直到 srtt。
但千万别把这当教条，在早期网络或者如今的 iot 网络上，乱序可以乱几百个 rtt，只在概率上，上述推理是足的。量 = 速率*时间，这是线性保证，但现实中要按统计规律算，为啥还是算术平均 1/4 minrtt，那是算术期望，这就是排队论的事了，不多说，周末愉快。
浙江温州皮鞋湿，下雨进水不会胖。
相关文章：
tcp early retransmit 和 rack 中神奇的 1/4 minrtt
雨中跑步十公里，沿河看柳，发了一则朋友圈： 为什么采用 1/4 minrtt 作为重传和探测的延时，上图解释的已经很清楚了，主要还是怕乱序，关于乱序的度量，上图解释得非常清楚，乱序预期可在…...
【强化学习实践】Gym+倒立单摆+创建自己的环境
一、Gym Gym是OpenAI开发的一个强化学习算法测试环境集合包。Gym提供了多种标准的环境，包括经典的游戏（如Atari游戏）、机器人模拟任务以及其他各种类型的问题，供开发者测试和训练强化学习智能体。在Gym环境中，开发者可…...
实习记录小程序|基于SSM的实习记录小程序设计与实现(源码+数据库+文档)
知识管理 目录 基于SSM的习记录小程序设计与实现 一、前言 二、系统设计 三、系统功能设计 1、小程序端： 2、后台 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取： 博主介绍：✌️大厂码农|毕…...
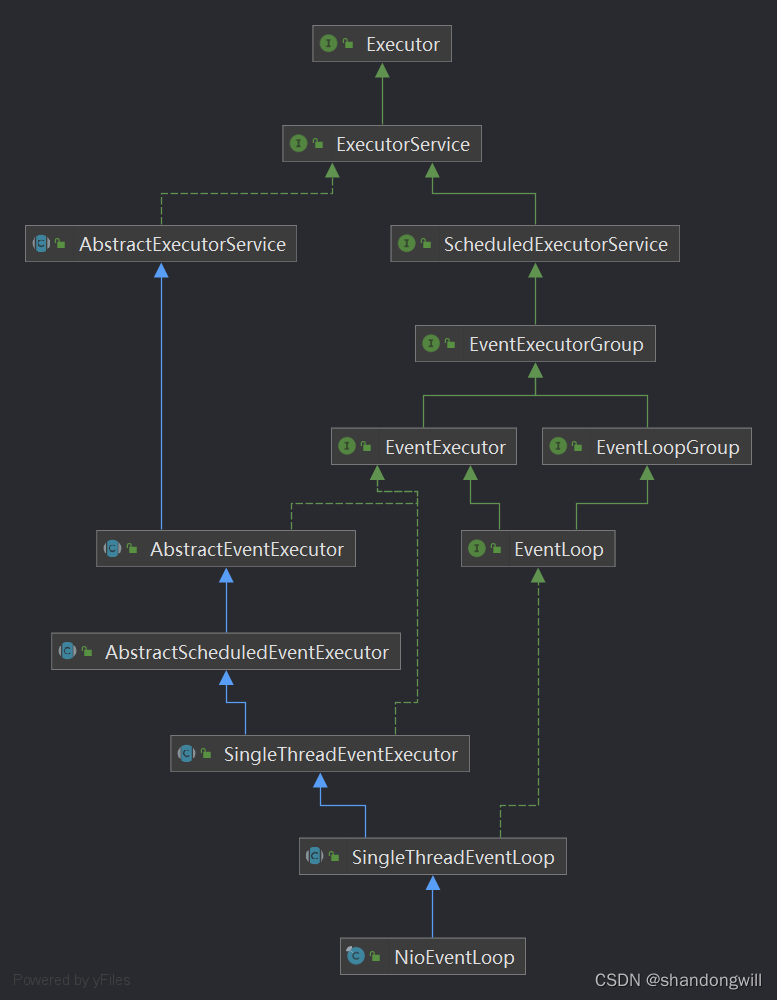
Netty NioEventLoop详解
文章目录 前言类图主要功能NioEventLoop如何实现事件循环NioEventLoop如何处理多路复用Netty如何管理Channel和Selector管理Channel管理Selector注意事项 前言 Netty通过事件循环机制(EventLoop)处理IO事件和异步任务，简单来说，就是通过一个死循环&…...
互联网大厂常见面试题目
1. CPU 的内存结构分为哪几层，分别是用于放什么数据的，如果一个函数里面有全局变量，局部变量和静态变量数据是如何存放的 2.C多态的实现原理是什么，父类是如何找到子类的虚函数实现的 3.操作系统中的虚拟内存实现机制是什么&…...
TechTool Pro for Mac v19.0.3中文激活版 硬件监测和系统维护工具
TechTool Pro for Mac是一款专为Mac用户设计的强大系统维护和故障排除工具。它凭借全面的功能、高效的性能以及友好的操作界面，赢得了广大用户的信赖和好评。 软件下载：TechTool Pro for Mac v19.0.3中文激活版 作为一款专业的磁盘和系统维护工具&#x…...
Linux-docker安装数据库redis
1.拉取redis镜像 docker pull redis # 下载最新的redis版本 docker pull redis:版本号 # 下载指定的redis版本ps：我这是已经下载最新版本的redis 2.查看redis镜像 docker images3.创建挂在路径并授权 mkdir -p /usr/local/redis/data mkdir -p /usr/local…...
LisJson解析配置表
每日一句：南来北往，不辜负生活，不迷失方向 [{ "ID": 0, "Name": "SmallPeople", "InitHealth": 100, "CostGold": 0, "MoveSpeed": 1…...
剑指offer10.斐波那契数列（动态规划）
写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下： F(0) 0, F(1) 1 F(N) F(N - 1) F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始&#x…...
HarmonyOS实战开发-WebSocket的使用。
介绍 本示例展示了WebSocket的使用，包括客户端与服务端的连接和断开以及客户端数据的接收和发送。 WebSocket连接：使用WebSocket建立服务器与客户端的双向连接，需要先通过createWebSocket方法创建WebSocket对象，然后通过connect…...
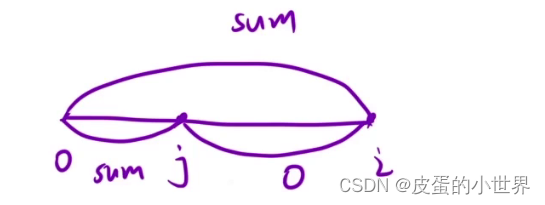
【前缀合】Leetcode 连续数组
题目解析 525. 连续数组 寻找一个子数组，这个子数组中包含相同数目的0和1，但是这个子数组需要最长的 算法讲解 只需在[0,i]寻找一段区间使得这一段区间的和也等于sum即可 细节问题：1. 这里的哈希表的value存的是下标，因为需要找…...
一些优雅的算法（c++）
求最大公约数：辗转相除法 int gcd(int a,int b){return b0?a:gcd(b,a%b); }求最小公倍数：两整数之积除以最大公约数 int lcm(int a, int b){return a*b / gcd(a, b); }十进制转n进制： char get(int x){if(x<9){return x0;}else{return…...
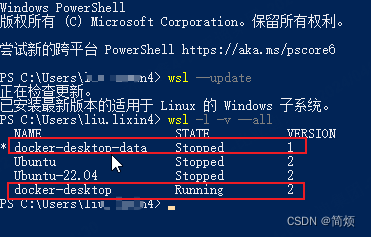
Docker Desktop修改镜像存储路径 Docker Desktop Start ... 卡死
1、CMD执行wsl -l -v --all 2、Clean / Purge data 3、导出wsl子系统镜像: wsl --export docker-desktop D:\docker\wsl\distro\docker-desktop.tar wsl --export docker-desktop-data D:\docker\wsl\data\docker-desktop-data.tar4、删除现有的wsl子系统： wsl -…...
小型企业网络安全指南
许多小型企业刚刚起步，没有大公司所拥有的相同资源来保护其数据。他们不仅可能没有资金来支持多样化的安全计划，而且也可能没有人力或时间。 网络犯罪分子知道小型企业缺乏这些资源，并利用这些资源来谋取利益。遭受网络攻击后，小…...
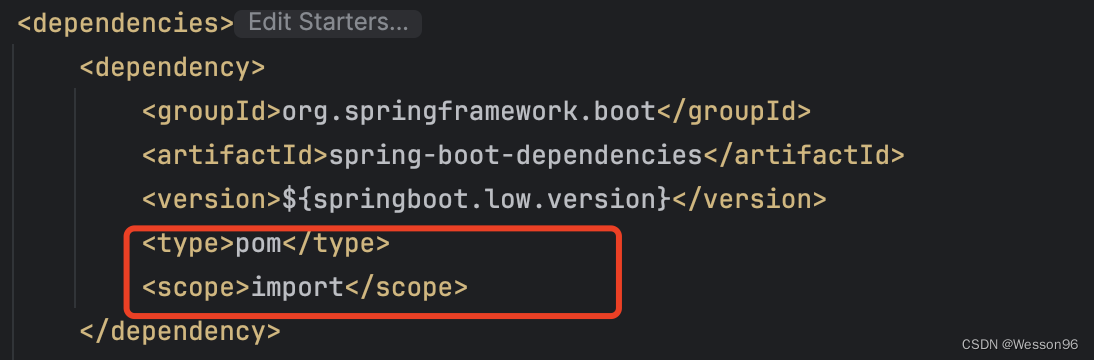
springboot相关报错解决
Caused by: java.lang.ClassNotFoundException: 目录 Caused by: java.lang.ClassNotFoundException: org.springframework.context.event.GenericApplicationListener spring-boot-dependencies:jar:2.1.9.RELEASE was not found org.springframework.context.event.Generi…...
python 中 from import, __name__, __all__, __init__.py 作用，python的模块和导入包
from import 即类似于其他语言一样，是为了将别人写好的 .py 文件引入，并用于自己使用 例如我在一个.py 文件中写了很多用于计数学计算的方法，当别人想要调用我写好的这一套方法时 就需要先 from 我写的文件或其他人写好的文件（py…...
Composer安装与配置详解
目录 第一章：Composer简介 1.1 什么是Composer？ 1.2 Composer与传统的依赖管理工具的区别 1.3 Composer的发展历程 1.4 本章小结 第二章：Composer安装 2.1 全局安装与项目内安装 2.1.1 全局安装 安装步骤 2.1.2 项目内安装 安装步骤 2.2 不同操作系统下的安装方…...
A5 STM32_HAL库函数 之 CAN通用驱动程序所有函数的介绍及使用
A5 STM32_HAL库函数 之 CAN通用驱动程序所有函数的介绍及使用 1 CAN通用驱动程序所有函数预览1.1 HAL_CAN_Init1.2 HAL_CAN_ConfigFilter1.3 HAL_CAN_DeInit1.4 HAL_CAN_MspInit1.5 HAL_CAN_MspDeInit1.6 HAL_CAN_Transmit1.7 HAL_CAN_Transmit_IT1.8 HAL_CAN_Receive1.9 HAL_C…...
python如何判断图片为黑白还是彩色
基本原理 灰度图分两种情况： 单通道的图片 RGB 三通道的图片，但是每个通道的值相等 对于单通道的图片只需要判断图片的通道值是否为1 对于RGB模式的图片，情况稍稍复杂些。理论上只需判断RGB三个通道的值是否相等，但是现实中灰度…...
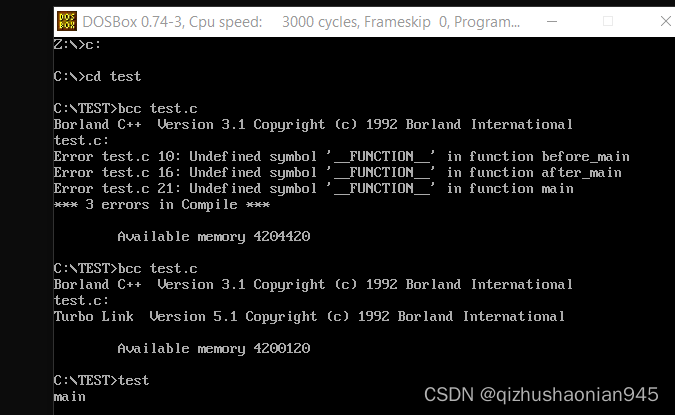
C语言进阶课程学习记录-main函数与命令行参数
C语言进阶课程学习记录-main函数与命令行参数 main函数验证以下4中定义是否正确实验-main的返回值cmd窗口 实验-main的输入参数cmd窗口 在main函数执其执行的函数实验-程序执行的第一个函数gcc编译器cmd窗口bcc编译器 小结 本文学习自狄泰软件学院 唐佐林老师的 C语言进阶课程&…...
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...
令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结： 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析： 实际业务去理解体会统一注…...
Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库，专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性，并提供了一个通用的框架&…...
Go 语言并发编程基础：无缓冲与有缓冲通道
在上一章节中，我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道，它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人，点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置，详见说明文档 成功后，记录Webhook 2 API文档说明 点击设置说明 查看自…...
Unity中的transform.up
2025年6月8日，周日下午 在Unity中，transform.up是Transform组件的一个属性，表示游戏对象在世界空间中的“上”方向（Y轴正方向），且会随对象旋转动态变化。以下是关键点解析： 基本定义 transfor…...
快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
多模态大语言模型arxiv论文略读（112）
Assessing Modality Bias in Video Question Answering Benchmarks with Multimodal Large Language Models ➡️ 论文标题：Assessing Modality Bias in Video Question Answering Benchmarks with Multimodal Large Language Models ➡️ 论文作者：Jea…...
Vue3学习（接口，泛型，自定义类型，v-for，props）
一，前言 继续学习 二，TS接口泛型自定义类型 1.接口 TypeScript 接口（Interface）是一种定义对象形状的强大工具，它可以描述对象必须包含的属性、方法和它们的类型。接口不会被编译成 JavaScript 代码，仅…...